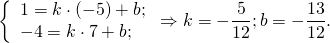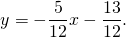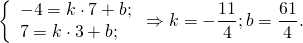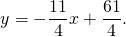Даны координаты вершин треугольника abc найти уравнение сторон угол между аб и бс

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте через точку, а не запятую. Округлять до -го знака после запятой. Содержание Уравнения сторон треугольника Даны координаты вершин треугольника abc найти уравнение сторон угол между аб и бс Даны координаты вершин треугольника А, В, С. Найти уравнения сторон АВ и АС и угол между ними. Сделать чертеж 💥 Видео Видео:Уравнения стороны треугольника и медианыСкачать Уравнения сторон треугольника Как составить уравнение сторон треугольника по координатам его вершин? Зная координаты вершин треугольника, можно составить уравнение прямой, проходящей через 2 точки. Дано: ΔABC, A(-5;1), B(7;-4), C(3;7) Составить уравнения сторон треугольника. 1) Составим уравнение прямой AB, проходящей через 2 точки A и B. Для этого в уравнение прямой y=kx+b подставляем координаты точек A(-5;1), B(7;-4) и из полученной системы уравнений находим k и b: Таким образом, уравнение стороны AB 2) Прямая BC проходит через точки B(7;-4) и C(3;7): Отсюда уравнение стороны BC — 3) Прямая AC проходит через точки A(-5;1) и C(3;7): Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать Даны координаты вершин треугольника abc найти уравнение сторон угол между аб и бс Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут Неправильный логин или пароль. Укажите электронный адрес и пароль. Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем. Инструкция по изменению пароля отправлена на почту. Чтобы зарегистрироваться, укажите ваш email и пароль Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности. Видео:Даны координаты вершин треугольника АВС.Скачать Даны координаты вершин треугольника А, В, С. Найти уравнения сторон АВ и АС и угол между ними. Сделать чертеж

Решение типового примера

Даны координаты вершин треугольника АВС: А(1, 2), В(3, 5), С(2, 3).Найти уравнения сторон АВ и АС и угол между ними.

Определим стороны АВ и АС треугольника АВС:

Рис. 1. Треугольник АВС

, то есть ,

, то есть .

Таким образом, угловые коэффициенты прямых соответственно равны

откуда получаем значение тангенса угла А

,

а угол определяем по таблицам или с помощью калькулятора:

.

Предел функции и непрерывность. Найти точки разрыва функции, если они существуют. Сделать чертеж функции

4.1
4.2
4.3
4.4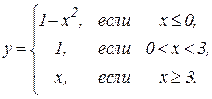
4.5
4.6
4.7
4.8
4.9
4.10
4.11
4.12
4.13
4.14
4.15
4.16
4.17
4.18
4.19
4.20

Решение типового примера

Найти точки разрыва функции если

На интервалах , и функция непрерывна, так как представляет собой элементарные функции. Проверке подлежат только точки x = -2 и x = 0.

Рассмотрим точку x = -2.

Вычислим односторонние пределы

,

.

Так как односторонние пределы не совпадают, но конечны, x=-2 – это точка разрыва функции 1-го рода.

Рассмотрим точку x=0:

,

.

X = 0 — точка непрерывности функции, так как в ней выполнено условие непрерывности (предел справа равен пределу слева).

Рис. 2. Точка разрыва первого рода

5 . Найти производные 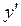указанных функций

5.1		5.11
5.2		5.12
5.3		5.13
5.4		5.14
5.5		5.15
5.6		5.16
5.7		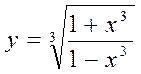5.17
5.8		5.18
5.9		5.19
5.10		5.20

Для нахождения производной функции надо воспользоваться правилами дифференцирования и таблицей производных.

Правила дифференцирования:

Если u(x) и v(x) — дифференцируемые функции, а c=const,

,	(1)
,	(2)
,	(3)
	(4)

Если u(x) и v(x) — дифференцируемые функции, то

.

(5)

Некоторые формулы из таблицы производных:

y=c, c=const	y’=0
Окончание таблицы

Примеры.Найти производные функций: а) ;

б) .

а) применяем правила дифференцирования сложной функции (5)

б) применяем правила дифференцирования произведения (3):

.

Вычислить предел функций, используя правило Лопиталя

№	а	б
6.1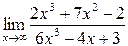
6.2
6.3
Продолжение таблицы
№	а	б
6.4
6.5
6.6
6.7
6.8
6.9
6.10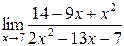
6.11
6.12.
6.13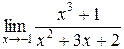
6.14
6.15
6.16
6.17
6.18
Окончание таблицы
№	а	б
6.19
6.20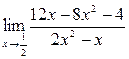

Примеры. Найти пределы, используя правило Лопиталя:

1. ; 2. .

Решение. Убедившись, что имеет место неопределенность или , применяем затем правило Лопиталя.

1. = ;

2.

.

В примере 2 правило Лопиталя применено дважды.

Найти интервалы монотонности и экстремумы функции.

7.1		7.11
7.2		7.12
7.3		7.13

Окончание таблицы
7.4		7.14
7.5		7.15
7.6		7.16
7.7		7.17
7.8		7.18
7.9		7.19
7.10		7.20

Пример:Найти интервалы монотонности и экстремумы функции .

1. Область определения — вся числовая ось, так как функция определена для любых значений х.

2. Множеством значений функции служит также вся числовая ось, так как функция непрерывна и при неограниченно возрастает, а при стремится к » «.

3. Функция является непрерывной и не имеет точек разрыва, так как дифференцируема во всех точках.

4. Для определения интервалов монотонности найдем производную:

.

Методом интервалов находим, что при функция является возрастающей, так ее производная положительна, а при — функция убывает, так как ее производная отрицательна.

Рис. 3. Интервалы монотонности

5. Точкой минимума функции является точка х=3, так как производная в ней обращается в ноль, а при переходе через нее меняет знак с минуса на плюс.

Точкой максимума функции является точка х=-1, так как производная в ней обращается в ноль, а при переходе через нее меняет знак с плюса на минус.

6. Находим значения функции в экстремумах:

Контрольная работа № 2

Задания

1. Найти площадь фигуры, ограниченной областью D:

1.1		1.11
1.2		1.12
1.3		1.13
1.4		1.14
1.5		1.15
1.6		1.16
1.7		1.17
1.8		1.18
1.9		1.19
1.10		1.20

Пример. Вычислить площадь фигуры, ограниченной областью D

Решение. Если на отрезке заданы две непрерывные функции , такие, что , то площадь фигуры, заключенной между этими кривыми на вычисляется по формуле: .

В данном случае площадь фигуры находим с помощью определенного интеграла от разности функций у = 4 и

Находим точки пересечения кривых и у = 4, значит, 4 = 2 x , откуда x = 2. Следовательно,

Рис. 1. Площадь криволинейной трапеции

Некоторые формулы таблицы интегралов

1.

2.

3.

4.

5. ,

Последнее изменение этой страницы: 2017-03-03; Просмотров: 1492; Нарушение авторского права страницы

💥 Видео

№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)Скачать

Вычисление медианы, высоты и угла по координатам вершинСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Вычисляем высоту через координаты вершин 1Скачать

найти уравнение высоты треугольникаСкачать

Найти площадь треугольника на векторахСкачать

ЧТО НАДО ГОВОРИТЬ ЕСЛИ НЕ СДЕЛАЛ ДОМАШКУ!Скачать

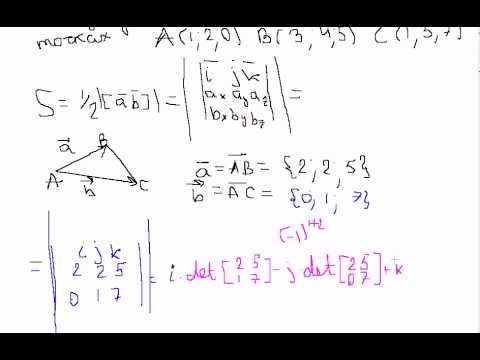
Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать

Уравнение прямой и треугольник. Задача про высотуСкачать

Метод координат. Как найти медиану треугольника, если известны координаты его вершин?Скачать

Угол между векторами | МатематикаСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

Уравнение годаСкачать

найти уравнения биссектрис углов между прямымиСкачать

Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Как находить угол между векторамиСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать