1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) | Примечание: дробные числа записывайте Округлять до -го знака после запятой. Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать  Решение математических задачДана система линейных уравнений: Доказать её совместность и решить двумя способами:
Докажем совместность системы. Составим расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду. rang(A)= rang()=3по теореме Кронекера-Капелли система совместна. 1) Решим систему по формулам Крамера: 2) Решим систему средствами матричного исчисления. Решение системы АХ=В находится по формуле: где А -1 — матрица, обратная к матрице А. А -1 находится по формуле: Даны векторы а(4; 7; 8),b (9; 1; 3),c(2; -4; 1) и d(1; -13; -13) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора d в этом базисе. Векторы образуют базис, если они линейно независимы. Условием линейной независимости векторов служит следующее условие: смешанное произведение векторов отлично от нуля. Вычислим смешанное произведение векторов . векторы линейно независимы, а значит образуют базис. Пусть координаты вектора в базисе следующие: . Разложение вектора по базису имеет вид: . Подставим координаты векторов: Решим систему методом Крамера: Ответ: координаты вектора в базисе следующие: (-2;1;0). Даны координаты вершины пирамиды А1А2А3А4:
1) Длина ребра А1А2 совпадает с длиной вектора 2) Угол между ребрами А1А2 И А1А4 найдем используя формулу скалярного произведения:
3) Угол между прямой (L) и плоскостью () Ax+By+Cz+D=0 находится по формуле: (m;n;p)-это координаты направляющего вектора прямой А1А4. Вектор является направляющим вектором прямой А1А4. Для нахождения уравнения плоскости, содержащей грань А1А2А3 используем уравнение плоскости, проходящей через три точки: 4) Площадь треугольника, построенного на векторах и находится по формуле: — векторное произведение векторов 5) Площадь пирамиды, построенной на векторах , и находится по формуле: где — смешанное произведение векторов. 6)Для нахождения уравнение прямой А1А2 воспользуемся каноническим уравнением прямой: где (m;n;p) — координаты направляющего вектора прямой А1А2. Вектор является направляющим вектором прямой А1А2.
Даны уравнения одной из сторон ромба x — 3y + 10 = 0 и одной его диагоналей x + 4y — 4 = 0; диагонали ромба пересекаются в точке P(0;1). Найти уравнения остальных сторон ромба. Сделать чертеж. Найдем точку М — точку пересечения стороны и диагонали: Диагонали ромба точкой пересечения делятся пополам, поэтому Р(0;1) — середина отрезка MN, где M и N противоположные вершины ромба. Запишем уравнение стороны NK, проходящей параллельно стороне (МТ): Если прямые параллельны, то их угловые коэффициенты равны.
— уравнение прямой NK Найдем уравнение второй диагонали ромба (ТК). Диагонали ромба перпендикулярны, поэтому их угловые коэффициенты связаны соотношением: .
Найдем точку Т — точку пересечения диагонали ТК и прямой МТ: Запишем уравнение прямой ТN, используя формулу прямой, проходящей через две точки:
— уравнение стороны ТN Сторона КМ параллельна стороне TN, поэтому угловые коэффициенты этих прямых равны.
— уравнение стороны МК Составить уравнение и построить линию, расстояние каждой точки которой от точки А (-1; 0) вдвое меньше расстояния ее от прямой x = -4. Пусть М(x;y) — точка, лежащая на искомой прямой. Расстояние от точки (х0;у0) до прямой Ах+Ву+С=0 определяется формулой: Расстояние от М до прямой равно: По условию задачи , т.е. Возведем обе части равенства в квадрат: — уравнение искомой линии. График полученной линии — парабола, ветви направлены вправо, вершина параболы в точке (-2,5;0), пересечение с осью ординат в точках (0;) и (0;). Линия задана уравнением в полярной системе координат
1) Построим линию по точкам, начиная от до и придавая значения через промежуток Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать  Даны координаты вершин пирамиды А1 А2 А3 А4. Средствами векторной алгебрыДаны координаты вершин пирамиды А1(2, 4, 3),
1) Определяем векторы А1А2 и А1А4: 2) площадь грани А1 А2 А3: 3) Проекция вектора А1А3 на вектор А1А4. 4) Объём пирамиды. 💡 ВидеоУравнения стороны треугольника и медианыСкачать  Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать  №973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать  Математика без Ху!ни. Уравнение плоскости.Скачать  Высшая математика. 4 урок. Аналитическая геометрия. Вычисление объема тетраэдра.Скачать 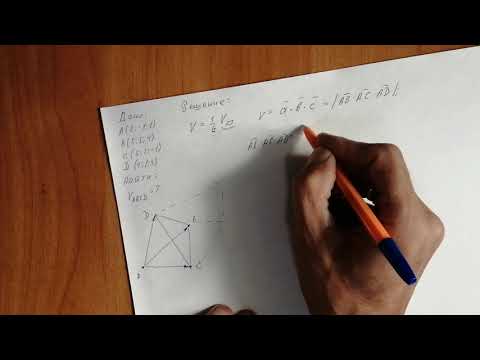 Аналитическая геометрия, 6 урок, Уравнение прямойСкачать  Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать  Что больше ★ 3^π или π^3 ★ Как сравнивать такие числа?Скачать  Найдите площадь треугольника АВС, если А(5;2;6), В(1;2;0), С(3;0;3)Скачать  Координаты точки и координаты вектора 1.Скачать  ОДИН плюс ОДИН - это МНОГО ★ Числовой РЕБУС ★ Как решать?Скачать  Уравнение прямой на плоскости. Решение задачСкачать  Уравнение прямой и треугольник. Задача про высотуСкачать  Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать  Составляем уравнение прямой по точкамСкачать  Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать  9 класс, 7 урок, Уравнение прямойСкачать  | |

































































































