Даны дифференциальные уравнения укажите среди них однородные уравнения (3 видео)

Содержание

Среди перечисленных дифференциальных уравнений укажите однородное уравнение
Однородные дифференциальные уравнения и приводящиеся к ним
Однородные уравнения
Уравнения, приводящиеся к однородным
Однородные дифференциальные уравнения
🔥 Видео

Видео:18+ Математика без Ху!ни. Дифференциальные уравнения. Однородное уравнение.Скачать

Среди перечисленных дифференциальных уравнений укажите однородное уравнение

Выберите один ответ:

Пока нет ответа

Найдите общее решение уравнения y — 9y = e2x

Выберите один ответ:

Пока нет ответа

Как называется решение, полученное из общего при конкретных значениях произвольных постоянных?

Выберите один ответ:

Пока нет ответа

Найдите общее решение уравнения

Выберите один ответ:

Пока нет ответа

Найдите общее решение уравнения (x+y)dx+xdy=0

Выберите один ответ:

Пока нет ответа

Среди перечисленных дифференциальных уравнений укажите уравнение Бернулли

Выберите один ответ:

Пока нет ответа

Найдите общее решение уравнения y—y= 0

Выберите один ответ:

Пока нет ответа

Найдите общее решение уравнения y— 4y+ 3y= 0

Выберите один ответ:

Пока нет ответа

Найдите общее решение уравнения xy2dy=(x3+y3)dx

Выберите один ответ:

Пока нет ответа

При решении каких уравнений используют подстановку ?

Выберите один ответ:

при решении линейных уравнений

при решении уравнений с разделяющими переменными

при решении однородных уравнений

Пока нет ответа

Найдите частное решение уравнения ds=(4t-3)dt, если при t= 0 s= 0

Выберите один ответ:

Пока нет ответа

Найдите общее решение уравнения

Выберите один ответ:

Пока нет ответа

Найдите общее решение уравнения y = cos x

Видео:4. Однородные дифференциальные уравнения (часть 1)Скачать

Однородные дифференциальные уравнения
и приводящиеся к ним

Видео:Дифференциальные уравнения, 3 урок, Однородные уравненияСкачать

Однородные уравнения

Функция называется однородной функцией своих аргументов измерения , если справедливо тождество .

Например, функция есть однородная функция второго измерения, так как

При имеем функцию нулевого измерения. Например, есть однородная функция нулевого измерения, так как

Дифференциальное уравнение вида называется однородным относительно и , если есть однородная функция своих аргументов нулевого измерения. Однородное уравнение всегда можно представить в виде

Вводя новую искомую функцию , уравнение (1) можно привести к уравнению с разделяющими переменными:

Если есть корень уравнения , то решение однородного уравнения будет или (прямая, проходящая через начало координат).

Замечание. При решении однородных уравнений необязательно приводить их к виду (1). Можно сразу делать подстановку .

Пример 1. Решить однородное уравнение .

Решение. Запишем уравнение в виде так что данное уравнение оказывается однородным относительно и . Положим , или . Тогда . Подставляя в уравнение выражения для и , получаем . Разделяем переменные: . Отсюда интегрированием находим

Так как , то, обозначая , получаем , где или . Заменяя на , будем иметь общий интеграл .

Отсюда общее решение: .

При разделении переменных мы делили обе части уравнения на произведение , поэтому могли потерять решение, которые обращают в ноль это произведение.

Положим теперь и . Но в силу подстановки , а из соотношения получаем, что , откуда . Непосредственной проверкой убеждаемся, что функции и также являются решениями данного уравнения.

Пример 2. Рассмотреть семейство интегральных кривых однородного уравнения . Показать, что касательные в соответственных точках к кривым, определяемым этим однородным дифференциальным уравнением, параллельны между собой.

Примечание: Будем называть соответственными те точки на кривых , которые лежат на одном луче, выходящем из начала координат.

Решение. По определению соответственных точек имеем , так что в силу самого уравнения , где и — угловые коэффициенты касательных к интегральным кривым и , в точках и соответственно (рис. 12).

Видео:Дифференциальные уравнения, 6 урок, Уравнения в полных дифференциалахСкачать

Уравнения, приводящиеся к однородным

А. Рассмотрим дифференциальное уравнение вида

где — постоянные, а — непрерывная функция своего аргумента .

Если , то уравнение (3) является однородным и оно интегрируется, как указано выше.

Если хотя бы одно из чисел отлично от нуля, то следует различать два случая.

1) Определитель . Вводя новые переменные и по формулам , где и — пока неопределенные постоянные, приведем уравнение (3) к виду

Выбирая и как решение системы линейных уравнений

получаем однородное уравнение . Найдя его общий интеграл и заменив в нем на , a на , получаем общий интеграл уравнения (3).

2) Определитель . Система (4) в общем случае не имеет решений и изложенный выше метод неприменим; в этом случае , и, следовательно, уравнение (3) имеет вид . Подстановка приводит его к уравнению с разделяющимися переменными.

Пример 3. Решить уравнение .

Решение. Рассмотрим систему линейных алгебраических уравнений

Определитель этой системы .

Система имеет единственное решение . Делаем замену . Тогда уравнение (5) примет вид

Это уравнение является однородным уравнением. Полагая , получаем

Интегрируя, найдем или .

Возвращаемся к переменным :

Пример 4. Решить уравнение .

Решение. Система линейных алгебраических уравнений несовместна. В этом случае метод, примененный в предыдущем примере, не подходит. Для интегрирования уравнения применяем подстановку , . Уравнение примет вид

Разделяя переменные, получаем

Возвращаясь к переменным , получаем общий интеграл данного уравнения

Б. Иногда уравнение можно привести к однородному заменой переменного . Это имеет место в том случае, когда в уравнении все члены оказываются одинакового измерения, если переменному приписать измерение 1, переменному — измерение и производной — измерение .

Пример 5. Решить уравнение .

Решение. Делаем подстановку , где пока произвольное число, которое мы выберем позже. Подставляя в уравнение выражения для и , получим

Заметим, что имеет измерение имеет измерение , имеет измерение . Полученное уравнение будет однородным, если измерения всех членов одинаковы, т.е. если выполняется условие , или .

Положим ; исходное уравнение принимает вид

Положим теперь . Тогда это уравнение примет вид , откуда .

Разделяем переменные в этом уравнении . Интегрируя, найдем

Заменяя через , получаем общий интеграл данного уравнения

Уравнение имеет еще очевидное решение , которое получается из общего интеграла при , если интеграл записать в виде , а затем перейти к пределу при . Таким образом, функция является частным решением исходного уравнения.

Видео:11. Уравнения в полных дифференциалахСкачать

Однородные дифференциальные уравнения

Однородное дифференциальное уравнение сводится к уравнению с разделяющимися переменными заменой y = xu, или, что тоже самое, , где u новая искомая функция. Действительно, тогда y’ = u + u’x и исходное уравнение может быть переписано в виде u + u’x = f(u), или u’x = f(u)u. Из последнего при f(u)u можем записать .

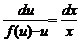
Пример. Решить уравнение (y 2 — 2xy)dx + x 2 dy = 0. Это однородное уравнение, так как y 2 — 2xy и x 2 однородные функции второй степени. Делаем замену y = xu, dy = udx + xdu. Подставляя в уравнение, имеем

(x 2 u 2 — 2x 2 u)dx + x 2 (udx + xdu) = 0.

Раскрывая скобки, приводя подобные и сокращая на x 2 , получаем уравнение с разделяющимися переменными

(u 2 — u)dx + xdu = 0

Разделяя переменные, получаем или, что то же самое, Интегрируя последнее соотношение, имеем lnu — ln(u-1) = lnx + lnC. Потенцируя (переходя от логарифмической функции к e x ), можем записать или, делая обратную замену , получаем общий интеграл уравнения

Уравнения вида приводятся к однородным переносом начала координат в точку пересечения прямых a₁x + b₁y +c₁ = 0, a₂x + b₂y +c₂ = 0, если определитель отличен от нуля, и заменой a₁x + b₁y = z, если этот определитель равен нулю.

Решить однородные уравнения онлайн можно с помощью специального сервиса Дифференциальные уравнения онлайн.