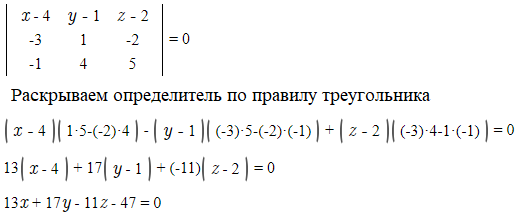Даны четыре точки a1 a2 a3 a4 составить уравнение

Условие

Даны четыре точки А1(х1, у1, z1), А2(х2, у2, z2), А3(х3, у3, z3), А4(х4, у4, z4). Составить уравнения:
а) плоскости А1А2А3;
б) прямой А1А2;
в) прямой А4М;
г) прямой А3К, параллельной прямой А1А2;
д) плоскости, проходящей через точку А4 перпендикулярно к прямой А1А2.

А1(4, 1, 2), А2(1, 2, 0), А3(3, 5, 7), А4(2, 3, 5)

Решение

a) Пусть M (x;y;z) — произвольная точка плоскости A_(1)A_(2)A_(3)
Тогда векторы
vector=(x-4;y-1;z-2)
vector<A_(1)A_>=(1-4;2-1;0-2)=(-3;1;-2)
vector<A_(1)A_>=(3-4;5-1;7-2)=(-1;4;5)

лежат в одной плоскости, значит компланарны.

Условие компланарности — равенство нулю определителя третьего порядка, составленного из координат этих векторов.

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Онлайн калькулятор. Уравнение плоскости

Предлагаю вам воспользоваться онлайн калькулятором чтобы найти уравнение плоскости.

Воспользовавшись онлайн калькулятором, вы получите детальное пошаговое решение вашей задачи, которое позволит понять алгоритм решения задач на составление уравнения плоскости и закрепить пройденный материал.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Найти уравнение плоскости

Выберите метод решения исходя из имеющихся в задаче данных:

В задаче известны:

Ввод данных в калькулятор для составления уравнения плоскости

В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.

Дополнительные возможности калькулятора для вычисления уравнения плоскости

• Используйте кнопки и на клавиатуре, для перемещения между полями калькулятора.

Теория. Уравнение плоскости.

Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки

В зависимости от условий задачи уравнение плоскости можно составить следующими способами:

Если заданы координаты трех точек A( x ₁, y ₁, z ₁), B( x ₂, y ₂, z ₂) и C( x ₃, y ₃, z ₃), лежащих на плоскости, то уравнение плоскости можно составить по следующей формуле

Если заданы координаты точки A( x ₁, y ₁, z ₁) лежащей на плоскости и вектор нормали n = , то уравнение плоскости можно составить по следующей формуле:

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Видео:4. Уравнение плоскости проходящей через три точки / в отрезках / доказательство и примерыСкачать

Уравнение прямой, проходящей через две точки онлайн

С помощю этого онлайн калькулятора можно построить уравнение прямой, проходящей через две точки. Дается подробное решение с пояснениями. Для построения уравнения прямой задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), введите координаты точек в ячейки и нажимайте на кнопку «Решить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Видео:Аналитическая геометрия, 5 урок, Уравнение плоскостиСкачать

Уравнение прямой, проходящей через две точки − примеры и решения

Пример 1. Построить прямую, проходящую через точки A(2, 1, 1), B(3, 1, -2).

(1)

Подставив координаты точек A и B в уравнение (1), получим:

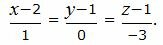(Здесь 0 в знаменателе не означает деление на 0).

Составим параметрическое уравнение прямой:

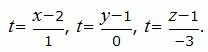Выразим переменные x, y, z через параметр t :

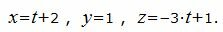Каноническое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:

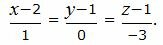Параметрическое уравнение прямой, проходящей через точки A(2, 1, 1), B(3, 1, -2) имеет следующий вид:

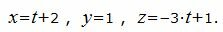Пример 2. Построить прямую, проходящую через точки A(1, 1/5, 1) и B(−2, 1/2, −2).

(2)

Подставив координаты точек A и B в уравнение (2), получим:

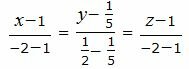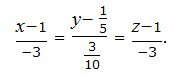Составим параметрическое уравнение прямой:

Выразим переменные x, y, z через параметр t :

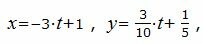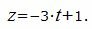Каноническое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

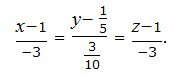Параметрическое уравнение прямой, проходящей через точки A(1, 1/5, 1) и B(−2, 1/2, −2) имеет следующий вид:

🎦 Видео

Уравнение плоскости через 3 точкиСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Высшая математика. 4 урок. Аналитическая геометрия. Вычисление объема тетраэдра.Скачать

Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Составляем уравнение прямой по точкамСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение окружности (1)Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Как проверить лежат ли 4 точки в одной плоскости Аналитическая геометрияСкачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Уравнение прямой на плоскостиСкачать

Составить уравнение прямой, проходящей через две данные точки. Метод координат. Геометрия 9 классСкачать

Математика без Ху!ни. Смешанное произведение векторовСкачать

№400. Даны точки A (3; — 1; 0), В (0; 0; — 7), С (2; 0; 0), D ( — 4; 0; 3), E (0; — 1; 0)Скачать

17. Показать что прямые пересекаются и составить уравнение плоскости в которой они расположеныСкачать