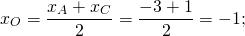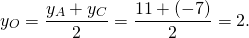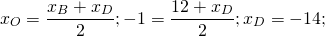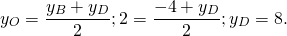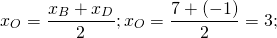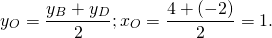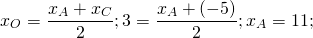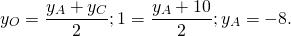Условие
4. Даны три последовательные вершины параллелограмма: А(2;4;3), В(-3; 0; 6), С(-4; 2; 1). Найти уравнения стороны AD и диагонали BD.
Решение
Диагонали параллелограмма в точке пересечения делятся пополам.
Координаты точки М как середины диагонали АС:
x_(М)=(x_(A)+x_(C))/2
y_(М)=(y_(A)+y_(C))/2
z_(М)=(z_(A)+z_(C))/2
Подставляем координаты точек А и С и находим координаты точки М
х_(М)=(2-4))/2 ⇒ х_(М)=-1
у_(М)=(4+2)/2 ⇒ у_(М)= 3
z_(М)=(3+1)/2 ⇒ z_(М)= 2
Координаты точки М как середины диагонали BD:
x_(М)=(x_(B)+x_(D))/2
y_(М)=(y_(B)+y_(D))/2
z_(М)=(z_(B)+z_(D))/2
Подставляем координаты точки B и М и находим координаты точки D
-1=(-3+x_(D))/2 ⇒ х_(D)=1
3=(0+у_(D))/2 ⇒ у_(D)= 6
2=(6+у_(D))/2 ⇒ у_(D)= -2
Уравнение стороны AD, как прямой проходящей через две точки
Уравнение диагонали BD, как прямой проходящей через две точки
Видео:№933. Найдите координаты вершины D параллелограмма ABCD, если А (0; 0), B (5; 0), С (12; -3.).Скачать
Найти четвертую вершину параллелограмма
Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?
В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.
Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.
Дано: ABCD — параллелограмм,
1) Найдём координаты точки O — середины диагонали AC.
2) По свойству диагоналей параллелограмма, точка O также является серединой BD:
Дано: ABCD — параллелограмм,
1) Ищем координаты точки O — середины отрезка BD:
2) Точка O также является серединой AC:
Видео:1. Векторы и параллелограмм задачи №1Скачать
2 Comments
А как вы получили -14 в первом примере.
Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.
Видео:Найдите вершину A параллелограмма ABCD, если B(3; −4; 7), C(−5; 3; −2) и D(1; 2; −3)Скачать
Даны три последовательные вершины параллелограмма ABCD: А (2; 2), В (4; 8) и С (-6; 10). Напишите уравнение прямой AD
Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать
Ваш ответ
Видео:Найдите длины диагоналей параллелограмма, построенного на векторах a=(1;-1;-4) и b=(-5;3;8)Скачать
решение вопроса
Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать
Похожие вопросы
- Все категории
- экономические 43,296
- гуманитарные 33,622
- юридические 17,900
- школьный раздел 607,211
- разное 16,830
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
🎦 Видео
Уравнения стороны треугольника и медианыСкачать
Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // ГеометрияСкачать
№974. Даны координаты вершин трапеции ABCD: А (-2; -2), В (-3; 1). Напишите уравненияСкачать
Задача по аналитической геометрииСкачать
Вычисляем высоту через координаты вершин 1Скачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Математика без Ху!ни. Смешанное произведение векторовСкачать
Уравнение прямой и треугольник. Задача про высотуСкачать
№9. Две смежные вершины и точка пересечения диагоналей параллелограмма лежат в плоскости αСкачать
Найти медиану треугольника, если даны три стороны. Геометрия 9 класс. Диагонали параллелограмма.Скачать
№363. Основанием пирамиды с вершиной О является параллелограмм ABCD, диагонали которогоСкачать
Площадь параллелограмма, построенного на данных векторахСкачать
18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать
Координаты середины отрезка. Уравнение средней линии или диагонали. Урок 4. Геометрия 8 класс.Скачать
