Дано уравнение прямой 3x 8y 24 0 тогда уравнение этой прямой в отрезках имеет вид

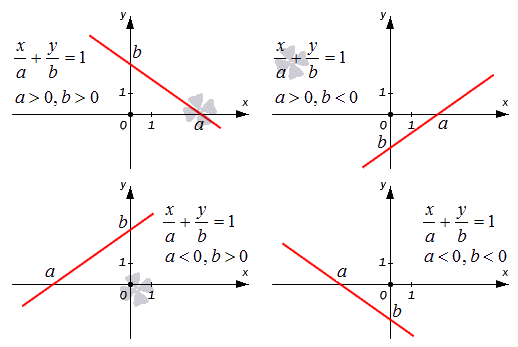
В данной статье мы рассмотрим уравнение прямой в отрезках. Представим методы преобразования уравнения прямой в отрезках в уравнение прямой в общем виде и обратно. Рассмотрим численные примеры.

Уравнение прямой в отрезках представляется следующей формулой:

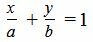(1)

где a и b числа, отличные от нуля.

Отметим, что числа a и b в уравнении (1) имеют простой геометрический смысл. Они равны длинам отрезков, которые отсекает прямая на осях Ox и Oy (Рис.1).

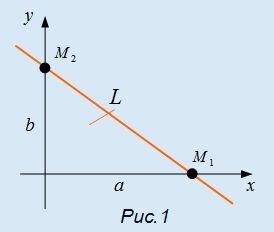Действительно. Подставляя в (1) y=0, получим x=a, если же подставить в (1) x=0, то получим y=b. Таким образом прямая L проходит через точки M₁(a, 0) и M₂(0, b).

Пример 1. Составить уравнение прямой, которая пересекает оси Ox и Oy в точках −1 и 3, соответственно.

Решение. Подставляя значения a=−1 и b=3 в (1), получим:

.

.

Видео:13. Общие уравнения прямой в пространстве / приведение к каноническому видуСкачать

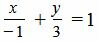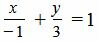Приведение уравнения прямой в отрезках к общему виду

Левая часть уравнения (1) приведем к общему знаменателю:

.

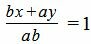Далее, умножив обе части уравнения на ab, получим:

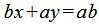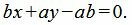Пример 2. Уравнение прямой в отрезках представлено следующим уравнением:

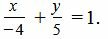Перевести уравнение к общему виду.

Решение. Приведем левую часть уравнения к общему знаменателю:

.

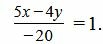Умножив обе части уравнения на −20, получим:

Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Приведение общего уравнения прямой на плоскости к уравнению прямой в отрезках

где A, B, C − отличные от нуля числа.

Сделаем следующие преобразования. Переведем свободный член C на правую часть уравнения и разделим обе части уравнения на −C:

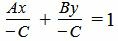(2)

Уравнение (2) можно переписать в следующем виде:

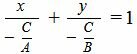(3)

Сделаем следующие обозначения:

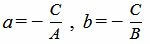Тогда получим уравнение прямой в отрезках (1).

Пример 3. Привести общее уравнение прямой

к уравнению прямой в отрезках.

Решение. Так как все коэффициенты уравнения отличны от нуля, можно построить уравнение прямой в отрезках. Воспользуемся формулой (3). Имеем: A=5, B=8, C=−3. Подставив эти значения в формулу (3), получим:

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение прямой в отрезках: описание, примеры, решение задач

Продолжаем изучение раздела «Уравнение прямой на плоскости» и в этой статье разберем тему «Уравнение прямой в отрезках». Последовательно рассмотрим вид уравнения прямой в отрезках, построение прямой линии, которая задается этим уравнением, переход от общего уравнения прямой к уравнению прямой в отрезках. Все это будет сопровождаться примерами и разбором решения задач.

Видео:§9 Уравнение прямой в отрезкахСкачать

Уравнение прямой в отрезках – описание и примеры

Пусть на плоскости расположена прямоугольная система координат O x y .

Прямая линия на плоскости в декартовой системе координат O x y задается уравнением вида x a + y b = 1 , где a и b – это некоторые действительные числа, отличные от нуля, величины которых равны длинам отрезков, отсекаемых прямой линией на осях O x и O y . Длины отрезков считаются от начала координат.

Как мы знаем, координаты любой из точек, принадлежащих прямой линии, заданной уравнением прямой, удовлетворяют уравнению этой прямой. Точки a , 0 и 0 , b принадлежат данной прямой линии, так как a a + 0 b = 1 ⇔ 1 ≡ 1 и 0 a + b b = 1 ⇔ 1 ≡ 1 . Точки a , 0 и b , 0 расположены на осях координат O x и O y и удалены от начала координат на a и b единиц. Направление, в котором нужно откладывать длину отрезка, определяется знаком, который стоит перед числами a и b . Знак « — » обозначает, что длину отрезка необходимо откладывать в отрицательном направлении координатной оси.

Поясним все вышесказанное, расположив прямые относительно фиксированной декартовой системы координат O x y на схематическом чертеже. Уравнение прямой в отрезках x a + y b = 1 применяется для построения прямой линии в декартовой системе координат O x y . Для этого нам необходимо отметить на осях точки a , 0 и b , 0 , а затем соединить эти точки линией при помощи линейки.

На чертеже показаны случаи, когда числа a и b имеют различные знаки, и, следовательно, длины отрезков откладываются в разных направлениях координатных осей.

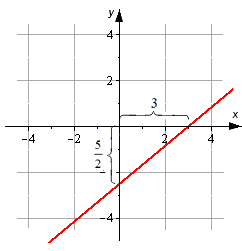
Прямая линия задана уравнением прямой в отрезках вида x 3 + y — 5 2 = 1 . Необходимо построить эту прямую на плоскости в декартовой системе координат O x y .

Решение

Используя уравнение прямой в отрезках, определим точки, через которые проходит прямая линия. Это 3 , 0 , 0 , — 5 2 . Отметим их и проведем линию.

Видео:Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Приведение общего уравнения прямой к уравнению прямой в отрезках

Переход от заданного уравнения прямой к уравнению прямой в отрезках облегчает нам решение различных задач. Имея полное общее уравнение прямой, мы можем получить уравнение прямой в отрезках.

Полное общее уравнение прямой линии на плоскости имеет вид A x + B y + C = 0 , где А , В и C не равны нулю. Мы переносим число C в правую часть равенства, делим обе части полученного равенства на – С . При этом, коэффициенты при x и y мы отправляем в знаменатели:

A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1

Для осуществления последнего перехода мы воспользовались равенством p q = 1 q p , p ≠ 0 , q ≠ 0 .

В результате, мы осуществили переход от общего уравнения прямой A x + B y + C = 0 к уравнению прямой в отрезках x a + y b = 1 , где a = — C A , b = — C B .

Разберем следующий пример.

Осуществим переход к уравнению прямой в отрезках, имея общее уравнение прямой x — 7 y + 1 2 = 0 .

Решение

Переносим одну вторую в правую часть равенства x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .

Делим обе части равенства на — 1 2 : x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .

Преобразуем полученное равенство к нужному виду: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .

Мы получили уравнение прямой в отрезках.

Ответ: x — 1 2 + y 1 14 = 1

В тех случаях, когда прямая линия задана каноническим или параметрическим уравнением прямой на плоскости, то сначала мы переходим к общему уравнению прямой, а затем уже к уравнению прямой в отрезках.

Перейти от уравнения прямой в отрезках и общему уравнению прямой осуществляется просто: мы переносим единицу из правой части уравнения прямой в отрезках вида x a + y b = 1 в левую часть с противоположным знаком, выделяем коэффициенты перед неизвестными x и y .

x a + y b = 1 ⇔ x a + y b — 1 = 0 ⇔ 1 a · x + 1 b · y — 1 = 0

Получаем общее уравнение прямой, от которого можно перейти к любому другому виду уравнения прямой на плоскости. Процесс перехода мы подробно разобрали в теме «Приведение общего уравнения прямой к другим видам уравнения прямой».

Уравнение прямой в отрезках имеет вид x 2 3 + y — 12 = 1 . Необходимо написать общее уравнение прямой на плоскости.

Решение

Действует по заранее описанному алгоритму:

x 2 3 + y — 12 = 1 ⇔ 1 2 3 · x + 1 — 12 · y — 1 = 0 ⇔ ⇔ 3 2 · x — 1 12 · y — 1 = 0

Ответ: 3 2 · x — 1 12 · y — 1 = 0

Видео:9 класс, 7 урок, Уравнение прямойСкачать

Дано уравнение прямой 3x 8y 24 0 тогда уравнение этой прямой в отрезках имеет вид

Общее уравнение прямой 4x — 3y + 12 = 0 представить в виде: 1) с угловым коэффициентом; 2) в отрезках на осях и 3) в нормальном виде. Построить эту прямую.

1) Уравнение прямой с угловым коэффициентом имеет вид y = kx + b. Чтобы заданное уравнение преобразовать к этому виду, разрешим его относительно y: 3y = 4x + 12, .

Сравнивая с уравнением y = kx + b, видим, что здесь угловой коэффициент прямой , а величина отрезка, отсекаемого прямой на оси ординат, b = 4 (если уравнение прямой дано в общем виде Ax + By + C = 0, то ее угловой коэффициент легко получить, если разделить коэффициент при x на коэффициент при y и взять полученное частное с обратным знаком ).

2) В отрезках на осях уравнение прямой имеет вид

(1)

Чтобы определить величины отрезков, отсекаемых заданной прямой 4x — 3y + 12 = 0, поступим так: в уравнении прямой положим y = 0. Получаем 4x + 12 = 0, а x = -3. Значит, наша прямая пересекает ось Ox в точке с координатами (-3, 0) и в уравнении (1) величина отрезка a = -3.

Полагая в нашем уравнении x = 0, определим ординату точки пересечения прямой с осью ординат. Будем иметь

Точка пересечения прямой с осью ординат имеет координаты (0, 4), и в уравнении (1) величина отрезка b = 4.

Таким образом, наше уравнение в отрезках на осях будет иметь вид

📸 Видео

Уравнение прямой на плоскостиСкачать

Уравнение прямой, проходящей через две точки, и прямой, перпендикулярной заданной прямойСкачать

Видеоурок "Нормальное уравнение прямой"Скачать

найти уравнения биссектрис углов между прямымиСкачать

Уравнения прямой на плоскости | Векторная алгебраСкачать

Составляем уравнение прямой по точкамСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Видеоурок "Параметрические уравнения прямой"Скачать

§8.1 Общее уравнение прямой на плоскостиСкачать

Уравнение прямой.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Проекция точки на плоскость, проекция прямой на плоскость. Параллельные прямые.Скачать