Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.
- Нормальный вектор плоскости – определение, примеры, иллюстрации
- Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
- Нормальное уравнение плоскости
- Приведение общего уравнения плоскости к нормальному виду
- Нормальный вектор плоскости, координаты нормального вектора плоскости.
- Нормальный вектор плоскости – определение, примеры, иллюстрации.
- Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости по уравнению плоскости.
- 🎥 Видео
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Нормальный вектор плоскости – определение, примеры, иллюстрации
Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.
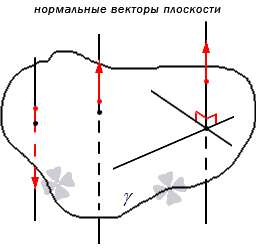
Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.
Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.
Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.
Рассмотрим на примере нормального вектора на плоскости.
Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .
Видео:1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости
Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.
Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .
По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.
Ответ: n → = ( 2 , — 3 , 7 ) .
Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .
По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .
Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .
При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .
Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.
Видео:5. Нормальное уравнение плоскости выводСкачать

Нормальное уравнение плоскости
В данной статье мы рассмотрим нормальное уравнение плоскости. Приведем примеры построения нормального уравнения плоскости по углу наклона нормального вектора плоскости от осей Ox, Oy, Oz и по расстоянию r от начала координат до плоскости. Представим метод приведения общего уравнения прямой к нормальному виду. Рассмотрим численные примеры.
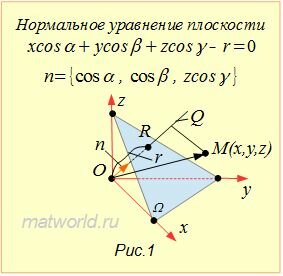
Пусть в пространстве задана декартова прямоугольная система координат. Тогда нормальное уравнение плоскости Ω представляется следующей формулой:
| xcosα+ycosβ+zcosγ−r=0, | (1) |
где r− расстояние от начала координат до плоскости Ω, а α,β,γ− это углы между единичным вектором n, ортогональным плоскости Ω и координатными осьями Ox, Oy, Oz, соответственно (Рис.1). (Если r>0, то вектор n направлен в сторону плоскости Ω, если же плоскость проходит через начало координат, то направление вектора n выбирается произвольной).
Выведем формулу (1). Пусть в пространстве задана декартова прямоугольная система координат и плоскость Ω (Рис.1). Проведем через начало координат прямую Q, перпендикулярную плоскости Ω, и точку пересечения обозначим через R. На этой прямой выделим единичный вектор n, с направлением, совпадающим с вектором 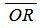
 |
Выразим уравнение плоскости Ω через следующие параметры: длину отрезка 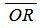
Так как вектор n является единичным вектором, то его проекции на Ox, Oy, Oz будут иметь следующие координаты:
| n=<cosα, cosβ, cosγ>. | (2) |
Обозначим через r расстояние от начала координат до точки R. Рассмотрим, теперь, точку M (x,y, z). Точка M лежит на плоскости Ω тогда и только тогда, когда проекция вектора 
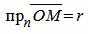 | (3) |
Скалярное произведение векторов n и 
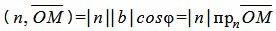 , , | (4) |
где 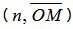


Поскольку n единичный вектор, то (4) можно записать так:
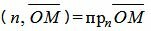 . . | (5) |
Учитывая, что n=<cosα, cosβ, cosγ>, 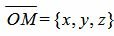
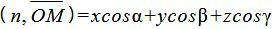 . . | (6) |
Тогда из уравнений (3), (5), (6) следует:
| xcosα+ycosβ+zcosγ=r, |
| xcosα+ycosβ+zcosγ−r=0. | (7) |
Мы получили нормальное уравнение плоскости Ω. Уравнение (7) (или (1)) называется также нормированным уравнением плоскости . Вектор n называется нормальным вектором плоскости .
Как было отмечено выше, число r в уравнении (1) показывает расстояние плоскости от начала координат. Поэтому, имея нормальное уравнение плоскости легко определить расстояние плоскости от начала координат. Для проверки, является ли данное уравнение плоскости уравнением в нормальном виде, нужно проверить длину нормального вектора этой плоскости и знак числа r, т.е. если |n|=1 и r>0, то данное уравнение является нормальным (нормированным) уравнением плоскости.
Пример 1. Задано следующее уравнение плоскости:
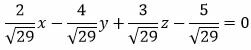 . . | (7) |
Определить, является ли уравнение (7) нормальным уравнением плоскости и если да, то определить расстояние данной плоскости от начала координат.
Решение. Нормальный вектор плоскости имеет следующий вид:
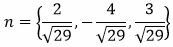 |
Определим длину вектора n:
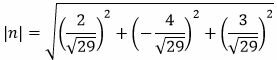 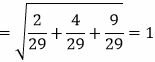 |
Ответ: Длина вектора n равна 1, 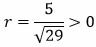
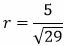
Видео:Уравнение плоскости через точку и нормальСкачать

Приведение общего уравнения плоскости к нормальному виду
| Ax+By+Cz+D=0. | (8) |
Так как уравнения (1) и (8) должны определять одну и ту же прямую (Утрерждение 2 статьи «Общее уравнение плоскости»), то существует такое число t, что
| tA=cosα, tB=cosβ, tC=cosγ, tD=−r. | (9) |
Возвышая в квадрат первые три равенства в (9) и складывая их, получим:
| (tA) 2 +(tB) 2 +(tС) 2 =cos 2 α+cos 2 β+cos 2 γ=1. | (10) |
Упростим выражение и найдем t:
| t 2 A 2 +t 2 B 2 +t 2 C 2 =t 2 (A 2 +B 2 +C 2 )=1, |
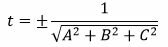 . . | (11) |
Знаменатель в (11) отличен от нуля, т.к. хотя бы один из коэффициентов A, B, C не равен нулю (в противном случае (8) не представлял бы уравнение прямой).
Выясним, какой знак имеет t. Обратим внимание на четвертое равенство в (9). Так как r−это расстояние от начала координат до плоскости, то r≥0. Тогда произведение tD должна иметь отрицательный знак. Т.е. знак t в (11) должен быть противоположным знаку D.
Подставляя в (1) вместо cosα, cosβ, cosγ и −r значения из (9), получим tAx+tBy+tCz+tD=0. Т.е. для приведения общего уравенения плоскости к нормальному виду, нужно заданное уравнение умножить на множитель (11). Множитель (11) называется нормирующим множителем .
Пример 2. Задано общее уравнение плоскости
| 2x−3y+6z+4=0. | (12) |
Построить нормальное уравнение плоскости (12).
Решение. Из уравнения (12) можно записать: A=2, B=−3, C=6, D=4. Вычислим t из равенства (11):
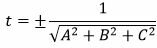 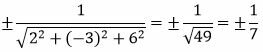 . . |
Так как D>0, то знак t отрицательный:
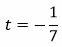 . . |
Умножим уравнение (12) на t:
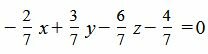 . . |
Ответ. Нормальное уравнение прямой (12) имеет следующий вид:
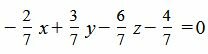 . . |
Отметим, что число 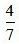
Видео:Векторы. Метод координат. Вебинар | МатематикаСкачать

Нормальный вектор плоскости, координаты нормального вектора плоскости.
Хорошее представление о прямой линии начинается с момента, когда вместе с ее образом одновременно возникают образы ее направляющих и нормальных векторов. Аналогично, при упоминании о плоскости в пространстве, она должна представляться вместе со своим нормальным вектором. Почему так? Да потому что во многих случаях удобнее использовать нормальный вектор плоскости, чем саму плоскость.
В этой статье мы сначала дадим определение нормального вектора плоскости, приведем примеры нормальных векторов и необходимые графические иллюстрации. Далее поместим плоскость в прямоугольную систему координат в трехмерном пространстве и научимся определять координаты нормального вектора плоскости по ее уравнению.
Навигация по странице.
Видео:Уравнение плоскости через 2 точки параллельно векторуСкачать

Нормальный вектор плоскости – определение, примеры, иллюстрации.
Для хорошего усвоения материала нам потребуется хорошее представление о прямой в пространстве, представление о плоскости и определения из статьи векторы – основные определения.
Дадим определение нормального вектора плоскости.
Нормальный вектор плоскости — это любой ненулевой вектор, лежащий на прямой перпендикулярной к данной плоскости.
Из определения следует, что существует бесконечное множество нормальных векторов данной плоскости.
Так как все нормальные векторы заданной плоскости лежат на параллельных прямых, то все нормальные векторы плоскости коллинеарны. Другими словами, если 



Также следует заметить, что любой нормальный вектор плоскости можно рассматривать как направляющий вектор прямой, перпендикулярной к этой плоскости.
Множества нормальных векторов параллельных плоскостей совпадают, так как прямая, перпендикулярная к одной из параллельных плоскостей, перпендикулярна и ко второй плоскости.
Из определения перпендикулярных плоскостей и определения нормального вектора плоскости следует, что нормальные векторы перпендикулярных плоскостей перпендикулярны.
Приведем пример нормального вектора плоскости.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz . Координатные векторы 

Видео:11 класс, 8 урок, Уравнение плоскостиСкачать

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости по уравнению плоскости.
Озвучим цель, которая преследовалась при создании этого пункта статьи: научиться находить координаты нормального вектора плоскости, если известно уравнение плоскости в прямоугольной системе координат Oxyz .
Общее уравнение плоскости вида 

Рассмотрим несколько примеров.
Найдите координаты какого-либо нормального вектора плоскости 
Нам дано общее уравнение плоскости, коэффициенты перед переменными x , y и z представляют собой соответствующие координаты нормального вектора этой плоскости. Следовательно, 

Плоскость задана уравнением 
Нам дано неполное уравнение плоскости. Чтобы стали видны координаты ее направляющего вектора, перепишем уравнение 



Уравнение плоскости в отрезках вида 

В заключении скажем, что с помощью нормального вектора плоскости могут быть решены различные задачи. Самыми распространенными являются задачи на доказательство параллельности или перпендикулярности плоскостей, задачи на составление уравнения плоскости, а также задачи на нахождение угла между плоскостями и на нахождение угла между прямой и плоскостью.
🎥 Видео
Видеоурок "Нормальное уравнение плоскости"Скачать

Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать

§42 Нормальное урaвнение плоскостиСкачать

Математика без Ху!ни. Взаимное расположение прямой и плоскости.Скачать

Векторный метод в стереометрии. Задача 14 профильный ЕГЭСкачать

Уравнение плоскости. Практическая часть. 11 класс.Скачать

Направляющий и нормальный вектор прямой на плоскости | Векторная алгебраСкачать

Вектор. Сложение и вычитание. 9 класс | МатематикаСкачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

9 класс, 2 урок, Координаты вектораСкачать

Задача 8. Написать уравнение плоскости, проходящей через точку перпендикулярно вектору.Скачать

§37 Общее и векторное уравнение плоскостиСкачать

Разложение вектора по базису. 9 класс.Скачать