Дано уравнение линии в полярной системе координат найти уравнение этой линии в декартовой системе (5 видео)

4.4. Уравнение линии в полярных координатах

По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса от полярного угла (аргумента). При этом полярный угол учитывается в радианах (!) и непрерывно принимает значения от до (иногда следует рассмотреть до бесконечности, или же в ряде задач для удобства от до ). Каждому значению угла «фи», которое входит в область определения функции , соответствует единственное значение полярного радиуса.

Полярную функцию можно сравнить со своеобразным радаром – когда луч света, исходящий из полюса, вращается против часовой стрелки и «прорисовывает» линию.

«Дежурным» примером полярной кривой является Архимедова спираль . На следующем рисунке изображен её первый виток – когда полярный радиус вслед за полярным углом принимает значения от 0 до :
Далее, пересекая полярную ось в точке , спираль продолжит раскручиваться, бесконечно далеко удаляясь от полюса. Но подобные случаи на практике встречаются довольно редко; более типичная ситуация, когда на всех последующих оборотах мы «пройдёмся по той же самой линии», которая получена в диапазоне .
В первом же примере мы сталкиваемся и с понятием области определения полярной функции: поскольку полярный радиус неотрицателен , то отрицательные углы у функции рассматривать нельзя.

! Примечание: в ряде случаев принято использовать обобщённые полярные координаты, где радиус может быть отрицательным, и такой подход мы вкратце изучим чуть позже

Кроме спирали Архимеда, есть множество других известных кривых, но искусством, как говорится, сыт не будешь, поэтому я подобрал примеры, которые очень часто встречаются в реальных практических заданиях.

Сначала простейшие уравнения и простейшие линии:

Уравнение вида задаёт луч, исходящий из полюса. Действительно, вдумайтесь, если значение угла всегда (каким бы ни было «эр») постоянно, то какая это линия?

Примечание: в обобщённой полярной системе координат данное уравнение задаёт прямую, проходящую через полюс.

Уравнение вида определяет… догадайтесь с первого раза – если для любого угла «фи» радиус остаётся постоянным? Фактически это определение окружности с центром в полюсе радиуса .

Например, . Для наглядности найдём уравнение этой линии в прямоугольной системе координат. Используя полученную ранее формулу , проведём замену:

Возведём обе части в квадрат:
– уравнение окружности с центром в начале координат радиуса 2, что и требовалось проверить.

А теперь оценИте удобство – с окружностью значительно выгоднее работать именно в полярных координатах по причине предельной простоты уравнения .

Рассмотрим более содержательные задачи на построение:

Задача 116

Построить линию

Решение: в первую очередь найдём область определения. Так как полярный радиус неотрицателен, то должно выполняться неравенство . Можно вспомнить школьные правила решения тригонометрических неравенств, но в простых случаях как этот,
я советую более быстрый графический метод решения:

– Посмотрим на график функции (см. Приложение Тригонометрия). Что означает неравенство ? Оно означает, что нас устраивает тот кусок графика, который не ниже оси абсцисс , а именно, его часть на отрезке . И, соответственно, интервал не подходит. Таким образом, область определения нашей функции: , то есть график расположен справа от полюса (по терминологии декартовой системы – в правой полуплоскости).

В полярных координатах часто бывает смутное представление о том, какую линию определяет то или уравнение, поэтому чтобы её построить, необходимо найти принадлежащие ей точки – и чем больше, тем лучше. Обычно ограничиваются десятком-другим (а то и меньшим количеством). Проще всего, конечно же, взять табличные значения угла.

Для бОльшей ясности к отрицательным значениям угла я буду «прикручивать» один оборот (левая колонка), и в силу чётности косинуса соответствующие положительные значения можно заново не считать (справа):

Изобразим полярную систему координат и отложим найденные точки, при этом одинаковые значения «эр» удобно откладывать за один раз, делая парные засечки циркулем по рассмотренной ранее технологии:

В принципе, линия отчётливо прорисовывается, но чтобы стопроцентно подтвердить догадку, давайте найдём её уравнение в декартовой системе координат. Можно применить недавно выведенные формулы , но я расскажу вам о более хитром приёме.

Обе части уравнения искусственно домножаем на «эр»: и используем более компактные формулы перехода:

Выделяя полный квадрат, приводим уравнение к понятному виду:

– уравнение окружности с центром в точке , радиуса 2.

Коль скоро по условию требовалось просто выполнить построение и всё, плавно соединяем найденные точки линией. Ничего страшного, если получится немного неровно, вы же не обязаны были знать, что это окружность 😉

Почему мы не рассмотрели значения угла вне промежутка ?

Ответ прост: нет смысла. Ввиду периодичности функции нас ждёт бесконечный «бег» по построенной окружности.

Несложно провести нехитрый анализ и прийти к выводу, что уравнение вида задаёт окружность диаметра с центром в точке .

Образно говоря, все такие окружности «сидят» на полярной оси и обязательно проходят через полюс. Если же , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).

Похожая задача для самостоятельного решения:

Задача 117

Построить линию и найти её уравнение в декартовой системе координат.

Систематизируем порядок решения задачи:

Находим область определения функции, для этого удобно посмотреть на синусоиду (Приложение Тригонометрия), чтобы сразу же понять, где синус неотрицателен.

На втором шаге рассчитываем полярные координаты точек, используя табличные значения углов; проанализируйте, нельзя ли сократить количество вычислений?

На третьем шаге откладываем точки в полярной системе координат и аккуратно соединяем их линией.

И, наконец, находим уравнение линии в декартовой системе координат.

Примерный образец решения в конце книги.

Общий алгоритм и технику построения в полярных координатах мы детализируем и существенно ускорим совсем скоро, но перед этим познакомимся ещё с одной распространённой линией:

Содержание

Лабораторная работа №2 «Полярная система координат»
Лабораторная работа №2 «Полярная система координат»
Задача 43787 .
Условие
Решение
Контрольная работа по мат. анализу 06
🎥 Видео

Видео:Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

Лабораторная работа №2 «Полярная система координат»

Видео:Построение кривой в полярной системе координатСкачать

Лабораторная работа №2 «Полярная система координат»

Цель работы: Ознакомиться с полярной системой координат. Изучить формулы, связывающие прямоугольные координаты Х и У точки М и ее полярные координаты.

1. Записать уравнения кривой (если необходимо) в явном виде:

2. Найти область определения функции , на основании чего сделать выводы о возможном расположении кривой.

3. Составить таблицу значений . Придавая значения углов на области определения функции .

4. Построить кривую в полярной системе по точкам с координатами

().

5. Записать формулы, связывающие декартовы, полярные координаты. С помощью этих формул в уравнении кривой перейти к заданию в декартовых координатах.

Для определения координат в декартовой системе координат используются координатные оси. Однако в ряде случаев удобно в качестве координат использовать не метрические величины, а величины других размерностей, например, углы.

Полярная система координат ставит в соответствие каждой точке на плоскости пару чисел (ρ; φ). Основными понятиями этой системы являются точка отсчета – полюс – и луч, начинающийся в этой точке, – полярная ось. Координата ρ – расстояние от точки до полюса, координата φ – угол между полярной осью и отрезком, соединяющим полюс и рассматриваемую точку, который берется со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «–» в противоположном случае. Важно понимать, что число φ в полярной системе определено не однозначно: парам чисел (ρ; φ + 2πn) соответствует одна и та же точка при любых натуральных n. Для полюса ρ = 0, а угол φ не определен.

Полярная система координат.

Полярные координаты легко преобразовать в декартовы. Пусть (x; y) – координаты точки в декартовой системе координат, (ρ; φ) – в полярной. Тогда очевидно, что

Формулы обратного перехода:

, , .

Следовательно, .

Пример. Линия задана уравнением в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ = 0 до φ = 2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой системе координат, у которой начало координат совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.

Решение: 1) Построим линию по точкам от φ = 0 до φ = 2π, придавая φ значения через промежуток .

Видео:Полярная система координатСкачать

Задача 43787 .

Условие

Даны уравнения линии r=r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам на промежутке от (φ)=0 до (φ)=2(π) с шагом, равным (π)/8; 2)найти уравнение линии в прямоугольной декартовой системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс- с полярной осью; 3)назвать линию, найти координаты центра и полуоси.

r=4/(2-3cos φ)

Решение

В полярной системе координат, откладывают лучи от начала О.
Эти лучи заполняют всю плоскость.

В условии задачи предлагают провести лучи
φ =0
φ =π/8
φ =2π/8=π/4
и так далее.

На каждом таком луче откладывается расстояние.

Например при φ =π/2
откладываем r=4/(2-3*0)=2

На луче откладываем расстояние только в одну сторону, т.е

4/(2-3cos φ ) >0 ⇒ 2-3cos φ >0 ⇒[b] cos φ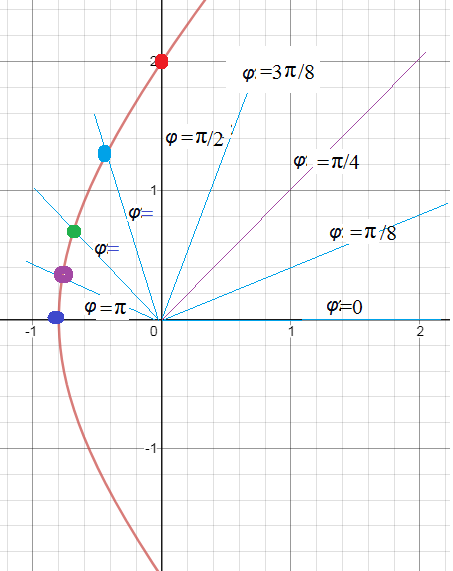

Видео:Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Контрольная работа по мат. анализу 06

Элементы векторной алгебры и аналитической геометрии

Контрольная работа 1

1. Даны координаты вершин пирамиды. Найти: 1) длину рёбер А1А2 и А1А3; 2) Угол между рёбрами А1А2 и А1А3; 3) Площадь грани А1А2А3; 4) Объём пирамиды; 5) Уравнение прямой А1А2; 6) Уравнение плоскости А1А2А3; 7) Угол между ребром А1А4 и гранью А1А2А3; 8) Уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Координаты вершин: А1(5;1;0), А2 (0;1;2), А3(3;0;1), А4(2;2;2).

Координаты векторов находим по формуле: X = xj — xi; Y = yj — yi; Z = zj — zi

Здесь X, Y,Z координаты вектора; xi, yi, zi — координаты точки Аi; xj, yj, zj — координаты точки Аj; Для вектора A1A2 : X = x2 — x1; Y = y2 — y1; Z = z2 — z1

X = 0-5; Y = 1-1; Z = 2-0

1) Длина рёбер А1А2 и А1А3;

Длина вектора a(X;Y;Z) выражается через его координаты формулой:

2) Угол между рёбрами А1А2 и А1А3;

Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:

, где a1a2 = X1X2 + Y1Y2 + Z1Z2

Найдем угол между ребрами A1A2 и A1A3

, γ = arccos(0.91) = 24.50

3) Площадь грани А1А2А3;

Найдем площадь грани с учётом геометрического смысла векторного произведения:

4) Объём пирамиды;

Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:

Находим Определитель матрицы

∆ = (-5) • ((-1) • 2-1 • 1)-(-2) • (0 • 2-1 • 2)+(-3) • (0 • 1-(-1) • 2) = 5

5) Уравнение прямой А1А2;

Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:

Уравнение прямой A1A2

6) Уравнение плоскости А1А2А3;

Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

Уравнение плоскости A1A2A3

(x-5)(0 • 1-(-1) • 2) — (y-1)((-5) • 1-(-2) • 2) + (z-0)((-5) • (-1)-(-2) • 0) = 2x+y+5z-11=0

7) Угол между ребром А1А4 и гранью А1А2А3;

Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле

8) Уравнение высоты, опущенной из вершины А4 на грань А1А2А3.

Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:

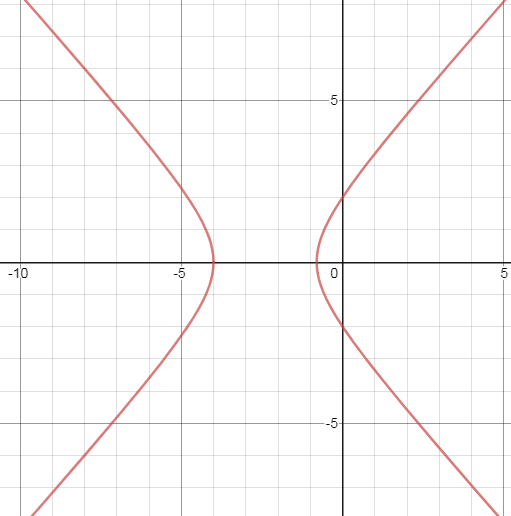
2. Линия задана уравнением В полярной системе координат

1. построить линию по точкам, начиная от До И придавая значения через промежуток ;

2. найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью;

3. по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

1) Построим линию по точкам, начиная от До и придавая Значения через промежуток

2) Построим уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.

3) Найдём уравнение данной линии в декартовой системе координат:

Используем формулы перехода от полярной системы координат к декартовой:

Тогда

По уравнению в декартовой прямоугольной системе координат определяем, что это линия — гипербола.

Элементы линейной алгебры

Контрольная работа 2

I. Даны две матрицы А и В. Найти (2АТ-3В)*(А+2ВТ)

, ,

II. Определить собственные значения и собственные векторы матрицы третьего порядка.

Исходная матрица имеет вид:

Составляем систему для определения координат собственных векторов:

(5 — λ)x1-2×2 + 2×3 = 0

0x1 + (5 — λ)x2 + 0x3 = 0

0x1 + 2×2 + (3 — λ)x3 = 0

Составляем характеристическое уравнение и решаем его.

Для этого находим определитель матрицы и приравниваем полученное выражение к нулю.

(5 — λ) • ((5 — λ) • (3 — λ)-2 • 0)-0 • (-2 • (3 — λ)-2 • 2)+0 • (-2 • 0-(5 — λ) • 2) = 0

После преобразований, получаем: — λ3 + 13λ2 — 55λ + 75 = 0

Один из корней уравнения равен λ1 = 3

Тогда характеристическое уравнение можно записать как

(λ -3)( — λ2 + 10λ — 25)=0.

D = 102 — 4 • (-1) • (-25) = 0

Получили собственные числа: λ1 = 3,

Найдём собственный вектор для λ1.

Составляем систему для определения координат собственных векторов:

Подставляя λ = 3 в систему, имеем:

Пусть x1 — свободное неизвестное, тогда выразим через него все остальные x1.

Множество собственных векторов, отвечающих собственному числу λ1= 3 , имеет вид: , где x1 — любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x1 = 1: .

Рассуждая аналогично, находим собственный вектор, отвечающий собственным числам:

. Следовательно, — любое,

Множество собственных векторов, отвечающих собственным числам , имеет вид: . При x1 = 1 и x3 = 0: , при x1 = 0 и x3 = 1: .

Ответ: Собственные числа: λ1=3, , собственные векторы: , , .

III. Дано комплексное число z. Требуется: 1) записать число z в алгебраической и тригонометрической формах; 2) Найти все корни уравнения w3+z=0

1) — алгебраическая форма

— тригонометрическая форма

2) Найдем корни уравнения w3 =0,

Применим формулу извлечения корней из комплексного числа:

, к=0,1,…,n-1

Так как a=, то

Контрольная работа 3

I. Найти пределы функций, не пользуясь правилом Лопиталя.

Использовали эквивалентности бесконечно малых величин при :

II. Задана функция . Найти точки разрыва функции, если они существуют. Сделать чертёж

Построим график заданной функции:

Функция определена на всём множестве чисел и неэлементарная.

Каждая из составляющих функций непрерывна на своём промежутке; заданная функция может иметь точки разрыва только в точках смены аналитических выражений, то есть в точках и .