Дано уравнение гиперболы 9x 2 16y 2 144

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Задача 28927 4.3.81) Найти расстояние между точками.

Условие

4.3.81) Найти расстояние между точками пересечения асимптот гиперболы
9х^2-16у^2 = 144 с окружностью, имеющей центр в правом фокусе гиперболы и проходящей через начало координат.

Решение

Канонический вид гиперболы:
(x^2/a^2)-(y^2/b^2)=1

[b] Уравнения асимптот гиперболы имеют вид:[/b]

[b]Фокусы гиперболы имеют координаты
F_(1)(-с;0) и F_(2)(с;0)
b^2=c^2-a^2[/b]

Разделим обе части уравнения на 144:
(9x^2/144)-(16у^2/144)=1
Канонический вид гиперболы:
(x^2/16)-(y^2/9)=1
a^2=16
b^2=9
Тогда
[b] уравнения асимптот гиперболы

c^2=b^2+a^2=9+16=25
[b]Фокусы гиперболы имеют координаты
F_(1)(-5;0) и F_(2)(5;0) [/b]

Уравнение окружности с центром в точке
F_(2) (5;0) и радиусом R=5 имеет вид

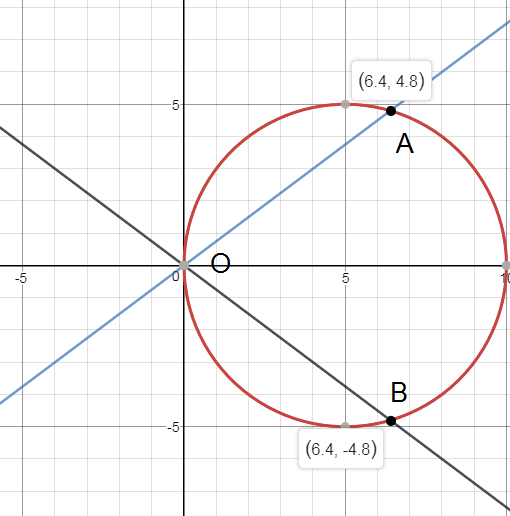
Чтобы найти точки пересечения гиперболы
асимптоты y=(-3/4)x
и
окружности
(x-5)^2+y^2=25
решим систему уравнений:

Подставим y=(-3/4)x во второе уравнение
(х-5)^2+((-3/4)x)^2 = 25;

Итак, асимптота y=(-3/4)x пересекается с окружностью
(х-5)^2+y^2=25 в точках
O(0;0) и А(6,4; — 4,8)
Аналогично, асимптота y=(3/4)x пересекается с окружностью (х-5)^2+y^2=25 в точках
O(0;0) и B(6,4; + 4,8)

О т в е т. 8; 9,6

Видео:Видеоурок "Гипербола"Скачать

На гиперболе 9х² — 16у² = 144 найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого?

Математика | 10 — 11 классы

На гиперболе 9х² — 16у² = 144 найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого.

Каноническое уравнение гиперболы

Очевидно, что для нашего случая

Фокусное расстояние находим из соотношения

Теперь осталось найти точки, расстояние от которых до (5 ; 0) в два раза больше, чем до ( — 5 ; 0)

Второе решение не подходит, т.

К. квадрат y не может быть отрицательным

Таким образом решением являются две точки :

Видео:Аналитическая геометрия: Эллипс, Парабола, Гипербола. Высшая математикаСкачать

Назови три числа, изображения которых на координатном луче находятся : а) правее точки A (25) б) левее точки B (118) в) правее точки C(2), но левее точки D (15) г) правеее точки E(7), но левее точки F?

Назови три числа, изображения которых на координатном луче находятся : а) правее точки A (25) б) левее точки B (118) в) правее точки C(2), но левее точки D (15) г) правеее точки E(7), но левее точки F(8) (спасибо вам заранее, а то я не понила) ^ _ ^.

Видео:Лекция 31.2. Кривые второго порядка. Гипербола.Скачать

Составить уравнение линии, для каждой точки которой расстояние до точки А (0 ; 1) вдвое меньше расстояния до прямой y = 4 ?

Составить уравнение линии, для каждой точки которой расстояние до точки А (0 ; 1) вдвое меньше расстояния до прямой y = 4 .

Видео:Написать каноническое уравнение гиперболы. Дан эксцентриситетСкачать

Запишите координаты всех точек, которые на координатной прямой расположены : а) левее точки с координатой 15 б) левее точки с координатой 27, но правее точки с координатой 12?

Запишите координаты всех точек, которые на координатной прямой расположены : а) левее точки с координатой 15 б) левее точки с координатой 27, но правее точки с координатой 12.

Видео:Аналитическая геометрия, 7 урок, Линии второго порядкаСкачать

Запишите координаты всех точек, которые на координатной прямой расположены?

Запишите координаты всех точек, которые на координатной прямой расположены.

А) левее точки с координатой 15

б) левее точки с координатой 27, но правее точки с координатой 12.

Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Сколько имеется точек с натуральными координатами, которые на координатной прямой расположены а)левее точки А(15) б) правее точки В(10) в) правее точки С (12), но левее точки D(22)?

Сколько имеется точек с натуральными координатами, которые на координатной прямой расположены а)левее точки А(15) б) правее точки В(10) в) правее точки С (12), но левее точки D(22).

Видео:§21 Каноническое уравнение гиперболыСкачать

Определить уравнение траектории точки M(x?

Определить уравнение траектории точки M(x.

Y), которая движется так, что ее расстояние от точки F( — 1.

0) остается вдвое меньше расстояния от прямой x = — 4.

Видео:ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать

Составить простейшие уравнение гиперболы если расстояние между ее вершинами равна 20 а расcтояние между фокусами 30?

Составить простейшие уравнение гиперболы если расстояние между ее вершинами равна 20 а расcтояние между фокусами 30.

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Даны координаты фокусов гиперболы — F1(4 ; 2) , F2( — 1 ; — 10) и уравнение касательной 3х + 4у — 5 = 0?

Даны координаты фокусов гиперболы — F1(4 ; 2) , F2( — 1 ; — 10) и уравнение касательной 3х + 4у — 5 = 0.

Найти параметр а гиперболы.

Видео:Неполное уравнение второго порядка. Эллипс, гипербола. ЗадачиСкачать

Составить каноническое уравнение параболы с вершиной в начале координат, симметричной ОУ , фокус которой в точке F(0 ; — 3) Составить уравнение эллипса , проходящего через точку А(4 ; 6) , фокусы кото?

Составить каноническое уравнение параболы с вершиной в начале координат, симметричной ОУ , фокус которой в точке F(0 ; — 3) Составить уравнение эллипса , проходящего через точку А(4 ; 6) , фокусы которого совпадают с фокусами гиперболы x ^ 2 — y ^ 2 = 8.

Видео:Новая задача №9 на гиперболу из ЕГЭ 2022 по математикеСкачать

Найти уравнение параболы, вершины которой находится в точке (3 ; 2) и фокус в точке (5 ; 2)?

Найти уравнение параболы, вершины которой находится в точке (3 ; 2) и фокус в точке (5 ; 2).

Вы перешли к вопросу На гиперболе 9х² — 16у² = 144 найти точки, расстояние которых от левого фокуса вдвое меньше, чем от правого?. Он относится к категории Математика, для 10 — 11 классов. Здесь размещен ответ по заданным параметрам. Если этот вариант ответа не полностью вас удовлетворяет, то с помощью автоматического умного поиска можно найти другие вопросы по этой же теме, в категории Математика. В случае если ответы на похожие вопросы не раскрывают в полном объеме необходимую информацию, то воспользуйтесь кнопкой в верхней части сайта и сформулируйте свой вопрос иначе. Также на этой странице вы сможете ознакомиться с вариантами ответов пользователей.

1)327 — 20 * x = 267 — 20x = 267 — 327 — 20x = — 60 x = — 60 : ( — 20) x = 60 : 20 x = 30 2)48 * x + 568 = 1000 48x = 1000 — 568 48x = 432 x = 432 : 48 x = 9 3)425 : x + 432 = 437 425 : x = 437 — 432 425 : x = 5 x = 425 : 5 x = 85.

327 — 20•x = 267 20 * x = 327 — 267 20 * x = 60 x = 60 : 20 x = 3 48•x + 568 = 1000 48 * x = 1000 — 568 48x = 432 x = 432 : 48 x = 9 425 : x + 432 = 437 425 : x = 437 — 432 425 : x = 5 x = 425 : 5 x = 85.

А) 7×4 = 28 б) 3×7 = 21 в) 12×3 = 36.

Если пять дней в неделю : 1. 70х5 = 350 — первая неделя 2. 80х5 = 400 — вторая неделя 3. 350 + 400 = 750 — итого Ответ : 750 Если шесть дней в неделю : 1. 70х6 = 420 — первая неделя 2. 80х6 = 480 — вторая неделя 3. 420 + 480 = 900 — итого Ответ..

28 двадцать восемь 60 шестьдесят 90 девяносто 100 сто 40 сорок.

2 дес 8 ед = 28 6 дес = 60 9 дес = 90 10 дес = 100 4 дес = 40.

НАИБОЛЬШОЕ 5 ЗНАЧНОЕ ЧИСЛО САСТАВЛЕНО И ЦЫФР 1 2 3 НАИБОЛЬШОЕ ЧИСЛО 33321 НАИМЕНЬШЕЕ 11123 ВЫЧЕТАЕМ ОДНО ИЗ ДРУГОГО 33321 — 11123 = 22198.

Наибольшее число : 33333 Наименьшее число : 11111 33333 — 11111 = 22222 Ответ : 2).

1)45 : 250 * 100% = 18% 2)18 / 50 * 100% = 36%.

Вместо / пиши дробь. 2 / 6 = 1 / 3 6 / 14 = 3 / 7 6 / 9 = 2 / 3 5 / 15 = 1 / 3 3 / 9 = 1 / 3 10 / 22 = 5 / 11 12 / 15 = 4 / 5 10 / 35 = 2 / 7 4 / 12 = 1 / 3 12 / 14 = 6 / 7 18 / 21 = 6 / 7 6 / 18 = 1 / 6 5 / 25 = 1 / 5 18 / 28 = 9 / 14 30 / 33 = 10 ..

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

Привести к каноническому виду

Виды выражений

Решение

Дано ур-ние линии 2-порядка:
$$9 x^ — 16 y^ + 144 = 0$$
Это уравнение имеет вид:
$$a_ x^ + 2 a_ x y + 2 a_ x + a_ y^ + 2 a_ y + a_ = 0$$
где
$$a_ = 9$$
$$a_ = 0$$
$$a_ = 0$$
$$a_ = -16$$
$$a_ = 0$$
$$a_ = 144$$
Вычислим определитель
$$Delta = left|begina_ & a_\a_ & a_endright|$$
или, подставляем
$$Delta = left|begin9 & 0\0 & -16endright|$$
$$Delta = -144$$
Т.к.
$$Delta$$
не равен 0, то
находим центр канонической системы координат. Для этого решаем систему уравнений
$$a_ x_ + a_ y_ + a_ = 0$$
$$a_ x_ + a_ y_ + a_ = 0$$
подставляем коэффициенты
$$9 x_ = 0$$
$$- 16 y_ = 0$$
тогда
$$x_ = 0$$
$$y_ = 0$$
Тем самым мы перешли к уравнению в системе координат O’x’y’
$$a’_ + a_ x’^ + 2 a_ x’ y’ + a_ y’^ = 0$$
где
$$a’_ = a_ x_ + a_ y_ + a_$$
или
$$a’_ = 144$$
$$a’_ = 144$$
тогда ур-ние превратится в
$$9 x’^ — 16 y’^ + 144 = 0$$
Данное уравнение является гиперболой
$$frac<tilde x^> — frac<tilde y^> = -1$$
— приведено к каноническому виду
Центр канонической системы координат в точке O

Базис канонической системы координат
$$vec e_1 = left ( 1, quad 0right )$$
$$vec e_2 = left ( 0, quad 1right )$$

Дано ур-ние линии 2-порядка:
$$9 x^ — 16 y^ + 144 = 0$$
Это уравнение имеет вид:
$$a_ x^ + 2 a_ x y + 2 a_ x + a_ y^ + 2 a_ y + a_ = 0$$
где
$$a_ = 9$$
$$a_ = 0$$
$$a_ = 0$$
$$a_ = -16$$
$$a_ = 0$$
$$a_ = 144$$
Инвариантами данного уравнения при преобразовании координат являются определители:
$$I_ = a_ + a_$$

подставляем коэффициенты
$$I_ = -7$$

$$I_ = left|begin9 & 0 & 0\0 & -16 & 0\0 & 0 & 144endright|$$
$$I = left|begin- lambda + 9 & 0\0 & — lambda — 16endright|$$

© Контрольная работа РУ — калькуляторы онлайн

Видео:Лекция 31.1. Кривые второго порядка. ЭллипсСкачать

Где учитесь?

Для правильного составления решения, укажите:

🔥 Видео

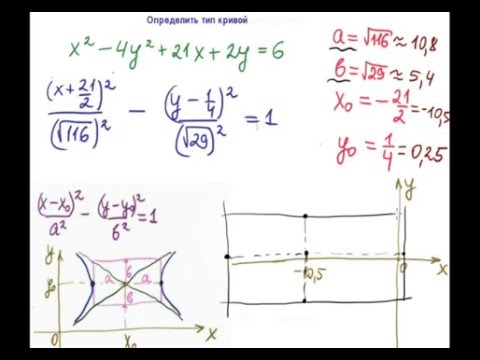
Определить тип кривой (гипербола)Скачать

Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

The eccentricity of the hyperbola `9x^(2)-16y^(2)+72x-32y-16=0`, isСкачать

§23 Построение гиперболыСкачать

Быстрый способ решения уравнения ➜ 9x⁴-6x³-18x²-2x+1=0Скачать

Кривые второго порядка. Эллипс. Приведение к каноническому виду и чертежСкачать