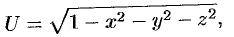Дано скалярное поле составить уравнение линии уровня и построить эту линию

Видео:Математика без Ху!ни. Функции нескольких переменных. Область определения. Линии уровня.Скачать

Скалярное поле. Векторное поле. Основные понятия и задачи

Видео:Поверхности и линии уровняСкачать

Понятие поля в математике

Теория поля является разделом математики, однако понятие поля лежит в основе многих представлений современной физики. В общем случае говорят, что в пространстве задано поле некоторой величины u , если в каждой точке пространства (или некоторой его части) определено значение этой величины. Так, например, при изучении потока газа приходится исследовать несколько полей: температурное поле (в каждой точке температура имеет определённое значение), поле давлений, поле скоростей и другие поля.

Поле величины u называется стационарным, (или установившимся), если u не зависит от времени t . В противном случае поле называется нестационарным (или неустановившимся). Таким образом, величина u есть функция точки M и времени t .

В задачах физики чаще всего приходится иметь дело со скалярными и векторными величинами. В соответствии с этим различают два вида полей: скалярные и векторные.

Видео:Построить поверхности уровня и линии уровня скалярного поляСкачать

Скалярное поле: определение, поверхности уровня и линии уровня

Пусть D — некоторая область на плоскости или в пространстве.

Определение скалярного поля. Если в области D каждой точке M(x,y,z) пространства или точке M(x,y) плоскости в каждый момент времени t по определённому закону ставится в соответствие значение скалярной величины u , то функция u(x,y,z,t) в случае пространства или u(x,y,t) в случае плоскости называется скалярным полем.

Понятия скалярного поля и функции, определённой в области D , совпадают.

Примером скалярного поля может служить поле температур воздуха в некотором помещении, если температуру рассматривать как функцию точки. В точках, расположенных ближе к источнику тепла, температура выше, чем в точках, расположенных дальше от источника тепла. Можно привести и такие примеры, как поле освещённости, поле плотности массы и тому подобные.

Для получения более полного представления о скалярном поле используется его графическое изображение — поверхности уровня в пространстве и линии уровня на плоскости.

Линии уровня широко используются при составлении топографических и метеорологических карт. На топографических картах линия уровня — линия, в точках которой отмечена одна и та же высота над уровнем моря. На метеорологических картах строят два вида линий уровня — изотермы (линии одинаковой температуры) и изобары (линии одинакового давления).

Определение. Поверхностью уровня скалярного поля называется множество всех тех точек пространства, в которых скалярное поле постоянно.

Уравнение поверхности уровня скалярного поля u(x,y,z) :

При постоянном изменении значения C поверхности уровня заполняют всю область пространства. Если поверхности уровня размещены плотно, скалярное поле изменяется быстро. Если же поверхности уровня расположены редко, скалярное поле изменяется медленно.

Определение. Линией уровня скалярного поля называется множество всех тех точек на плоскости, в которых скалярное поле постоянно.

Уравнение линии уровня скалярного поля u(x,y) :

Пример 1. Определить поверхности уровня скалярного поля и их вид.

Решение. Уравнением поверхностей уровня данного скалярного поля является

.

Поверхностями уровня являются конусы с вершиной в начале координат и осью вращения Oy . Так как по области определения , то одновременно не может быть x = 0 и z = 0 . Поэтому следует исключить вершину конусов.

Пример 2. Определить линии уровня скалярного поля и их вид.

Решение. Уравнением линий уровня данного скалярного поля является

.

Из этого уравнения выразим «игрек»:

.

Так как arcsinC — также константа, обозначим её C 1 . Тогда

Графиками этих линий являются параболы с вершиной в точках и ветвями вниз. На рисунке изображены линии уровня в трёх случаях: C 1 = 1 — красная линия, C 1 = 2 — зелёная линия, C 1 = 3 — синяя линия.

Видео:1. Функция двух переменныхСкачать

Векторное поле: определение, векторные линии

Понятие векторного поля во многом аналогично понятию скалярного поля.

Определение векторного поля. Если в некоторой области пространства каждой точке M по определённому закону ставится в соответствие вектор , то векторная функция называется полем вектора или векторным полем.

Таким образом, векторным полем является векторная функция точки пространства

Примерами векторного поля являются поля скорости и ускорения в текущей жидкости или газе, поле силы гравитации, поле интенсивности электростатического поля и тому подобные. Вообще, примером векторного поля может служить поле сил любой природы.

Мы будем рассматривать только стационарные векторные поля, то есть поля, не зависящие от времени.

Проекции вектора , соответствующего точке M , на координатные оси обозначим P = P(x,y,z) , Q = Q(x,y,z) , R = R(x,y,z) . Тогда векторное поле сможем задать через компоненты:

.

Таким образом, векторное поле можно определить тремя скалярными функциями P , Q , R . Пусть эти функции и их частные производные по переменным x,y,z являются непрерывными функциями.

Определение. Векторной линией называется линия, направление которой в каждой точке касательной совпадает с направлением вектора поля в этой точке (рисунок ниже).

Векторные линии поля силы обычно называют линиями силы, векторные линии поля скоростей потока жидкости или газа — векторами потока. У стационарного потока жидкости линии потока совпадают с траекториями частиц жидкости.

Уравнения векторных линий можно найти, решив систему дифференциальных уравнений

.

Пример 3. Найти линии вектора поля .

Решение. Так как , , , получаем систему дифференциальных уравнений

.

Из первого равенства получаем

где . Из последнего равенства следует . Таким образом, получаем

И получаем уравнения векторных линий данного векторного поля:

Видео:1 Линии уровняСкачать

Задача 57552 Дано скалярное поле u =u(х; у): а).

Условие

Дано скалярное поле u =u(х; у): а) составить уравнение линии уровня и = С и построить её график; 6) вычислить с помощью градиента производную скалярного поля и =и(х; у) в точке А по направлению вектора АВ U=U(x,y)

Решение

a)[m]x^2+y^2+4x+2y=C [/m]- уравнение линии

[m]x^2+4x+y^2+2y=C [/m]- уравнение линии

[m]x^2+4x+4+y^2+2y+1=C-5 [/m]-окружности с центром (-2;-1)

cos α =0
cos β =1

1 cпособ ( см. скрин 1)

====

Видео:Линии уровня и поверхности уровня функции многих переменныхСкачать

Поверхности и линии уровня скалярного поля

Поверхности и линии уровня

Рассмотрим скалярное поле, задаваемое функцией 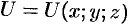. Для наглядного представления скалярного поля используют поверхности и линии уровня.

Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция 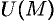принимает постоянное значение, т. е.

Давая в уравнении (70.1) величине с различные значения, получим различные поверхности уровня, которые в совокупности как бы расслаивают поле. Через каждую точку поля проходит только одна поверхность уровня. Ее уравнение можно найти путем подстановки координат точки в уравнение (70.1).

Для скалярного поля, образованного функцией

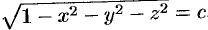
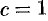
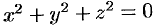
поверхностями уровня является множество концентрических сфер с центрами в начале координат: . В частности, при получим , т. е. сфера стягивается в точку.

Для равномерно раскаленной нити поверхности уровня температурного поля (изотермические поверхности) представляют собой, круговые цилиндры, общей осью которых служит нить.

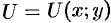
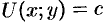
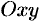
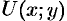
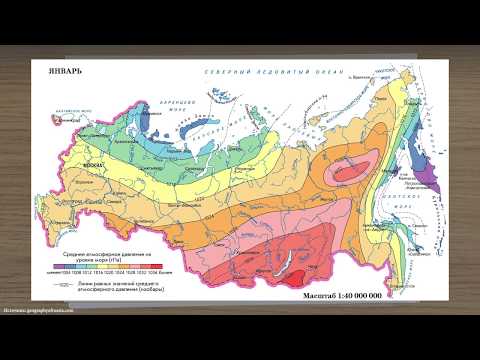
В случае плоского поля равенство представляет собой уравнение линии уровня поля, т. е. линия уровня — это линия на плоскости , в точках которой функция сохраняет постоянное значение.

В метеорологии, например, сети изобар и изотерм (линии одинаковых средних давлений и одинаковых средних температур) являются линиями уровня и представляют собой функции координат точек местности.

Линии уровня применяются в математике при исследовании поверхностей методом сечений (см. п. 12.9).

На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:

Другие темы по высшей математике возможно вам они будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

📺 Видео

2. Область определения функции двух переменныхСкачать

Градиент (пример, часть 2) + линия уровняСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Скалярное поле. ПрактикаСкачать

Градиент скалярного поляСкачать

Математика без Ху!ни. Частные производные функции нескольких переменных. Градиент.Скачать

Линии и поверхности уровня | ФНП 1.2Скачать

Функции двух переменных, линии уровня, частные производныеСкачать

Градиент, производная по направлению, производная сложной функции и полный дифференциалСкачать

2017. Градиент скалярной функции векторного аргумента. Линии уровня.Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать