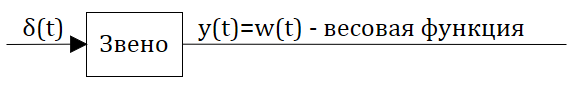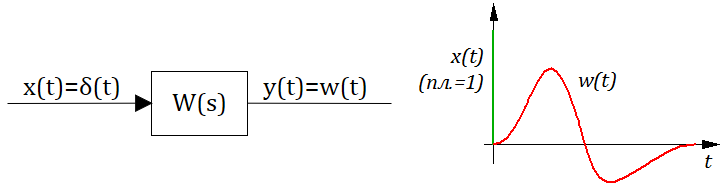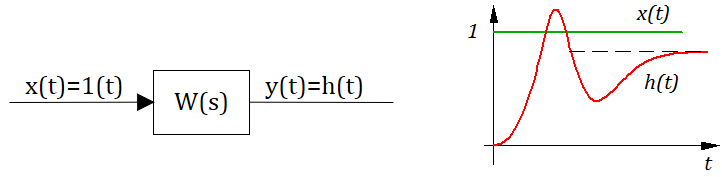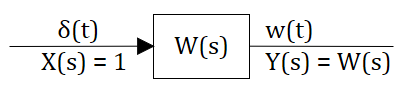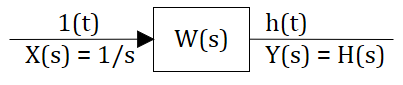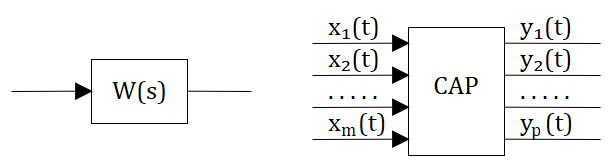Общее задание
 |
Дана одноконтурная САР, для которой определена передаточная функция регулятора (Р) с настройками и дифференциальное уравнение объекта управления (ОУ). Требуется определить:
— передаточную функцию разомкнутой системы W∞(s);
— характеристическое выражение замкнутой системы (ХВЗС);
— передаточные функции замкнутой системы Фз(s) – по заданию,
Фв(s) – по возмущению, ФЕ(s) – по ошибке;
— коэффициенты усиления САР;
Пример решения задания
Дан ПИ-регулятор с ПФ вида Wp = 2 + 

Определяется передаточная функция объекта:

Тогда передаточная функция разомкнутой системы имеет вид

D(s) = A(s) + B(s) = 2s 4 + 3s 3 + s 2 + 2s 3 + 9s 2 + 6s + 1 = 2s 4 + 5s 3 + 10s 2 + 6s + 1.
Передаточные функции замкнутой системы:


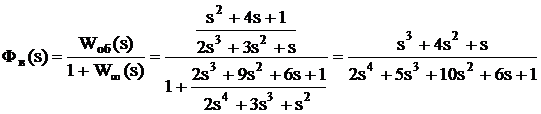
По передаточным функциям определяются коэффициенты усиления путем подстановки в них s = 0:
Устойчивость САР определяется по критерию Гурвица.
Поскольку коэффициенты ХВЗС а4 = 2, а3 = 5, а2 = 10, а1 = 6, а0 = 1 (степень полинома n = 4), то матрица Гурвица имеет вид
(обратите внимание на сходство строк матрицы: 1 с 3 и 2 с 4). Определители:
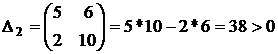
Поскольку все определители положительны, то САР устойчива. ♦
Варианты заданий
| Вариант | ПФ регулятора | Дифференциальное уравнение ОУ |
Wp = 4 +  ; ; |  | |
Wp = 5 +  ; ; |  | |
| Wp = 0,5 |  | |
Wp = 2 +  ; ; |  | |
Wp = 1 +  ; ; |  | |
| Wp = 4 |  | |
Wp = 5 +  ; ; |  | |
| Wp = 8 | 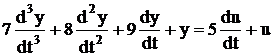 | |
Wp = 4 +  ; ; |  | |
Wp =  |  | |
Wp = 1 +  ; ; | 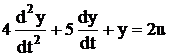 | |
Wp = 1 +  |  | |
Wp = 5 +  ; ; |  | |
Wp = 1 +  ; ; |  | |
Wp =  ; ; |  | |
Wp = 1 +  ; ; |  | |
Wp = 1 +  ; ; |  | |
| Wp = 2 |  | |
| Wp = 4 |  | |
Wp =  ; ; | 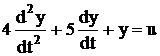 | |
Wp = 2 +  ; ; |  | |
Wp = 1 +  ; ; |  | |
Wp = 0,5 +  ; ; |  | |
| Wp = 0,1 |  | |
Wp = 0,2 +  ; ; |  | |
Wp = 2 +  ; ; |  |
Приложение В
Практические задания по теме «Идентификация объекта управления и определение настроек регулятора формульным методом»
Общее задание
По табличным данным построить переходную кривую объекта, определить параметры передаточной функции объекта, рассчитать настройки ПИД-регулятора, обеспечивающие 20%-ное перерегулирование.
Обозначены: DХ – входное воздействие объекта, DY – выходное, t — запаздывание объекта (в таблицу не включено).
Варианты заданий
Задание № 1. DX = 0,15 кг/см 2 ; DY = 24 °С; t = 1 мин
| t, мин | ||||||||||
| DY | 0,0 | 4,4 | 8,8 | 12,8 | 16,0 | 18,8 | 21,0 | 22,2 | 23,8 | 24,0 |
Задание № 2. DX = 15 кПа; DY = 150 мм; tзап = 0,15 мин
| t, мин | 0,00 | 0,25 | 0,50 | 0,75 | 1,00 | 1,25 | 1,50 | 1,75 | 2,00 | 2,25 | 2,50 | 2,75 | 3,00 |
| DY | 149,7 |
Задание № 3. DX = 90 м 3 /ч; DY = 45 °С; tзап = 0,1 мин
| t, мин | |||||||||||||
| DY | 0,0 | 5,5 | 16,0 | 25,5 | 31,5 | 35,0 | 38,0 | 40,0 | 41,7 | 43,0 | 43,8 | 44,5 | 45,0 |
Задание № 4. DX = 0,25 кг/см 2 ; DY = 8 °С; tзап = 1 мин
| t, мин | ||||||||||||||||
| DY | 0,00 | 0,10 | 1,30 | 2,75 | 3,90 | 4,90 | 5,70 | 6,30 | 6,70 | 7,20 | 7,50 | 7,70 | 7,85 | 7,95 | 8,00 | 8,00 |
Задание № 5. DX = 0,5 кг/см 2 ; DY = 36 °С; tзап = 1 мин
| t, мин | ||||||||||
| DY | 4,0 | 8,3 | 12,8 | 16,5 | 19,2 | 21,3 | 23,3 | 25,0 | 27,0 | 28,5 |
| t, мин | |||||||||||
| DY | 30,0 | 30,8 | 31,7 | 32,4 | 33,0 | 33,6 | 34,1 | 34,7 | 35,0 | 35,5 | 36,0 |
Задание № 6. DX = 0,1 кг/см 2 ; DY = 7 °С; tзап = 0,35 мин
| t, мин | ||||||||||||
| DY | 0,3 | 1,1 | 2,4 | 3,6 | 4,45 | 5,1 | 5,7 | 6,2 | 6,5 | 6,75 | 6,9 | 7,0 |
Задание № 7. DX = 0,25 кг/см 2 ; DY = 7,5 °С; tзап = 0,5 мин
| t, мин | 0,5 | |||||||||||||
| DY | 0,3 | 0,9 | 2,3 | 4,9 | 5,6 | 6,1 | 6,6 | 6,9 | 7,2 | 7,4 | 7,5 | 7,5 | 7,5 | 7,5 |
Задание № 8. DX = 0,055 кг/см 2 ; DY = 0,149 %; tзап = 40 с
| t, мин | |||||||||
| DY | 0,009 | 0,032 | 0,060 | 0,089 | 0,116 | 0,130 | 0,141 | 0,149 | 0,149 |
Задание № 9. DX = 0,2 кг/см 2 ; DY = 23 °С; tзап = 0,5 мин
| t, мин | |||||||
| DY | 0,6 | 1,8 | 3,6 | 5,8 | 8,2 | 11,2 | 16,4 |
| t, мин | |||||||
| DY | 18,2 | 20,2 | 21,4 | 22,4 | 22,6 | 22,8 |
Задание № 10. DX = 0,2 кг/см 2 ; DY = 30 °С; tзап = 1 мин
| t, мин |
| DY |
Задание № 11. DX = 0,3 кг/см 2 ; DY = 7,0 °С; tзап = 0,2 мин
| t, мин | 0,2 | 0,4 | 0,6 | 0,8 | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 |
| DY | 0,42 | 1,33 | 2,31 | 3,43 | 4,55 | 5,46 | 6,02 | 6,44 | 6,72 | 6,86 | 7,00 |
Задание № 12. DX = 0,25 кг/см 2 ; DY = 50 °С; tзап = 2 мин 45 с
| t, мин |
| DY |
Задание № 13. DX = 0,08 кг/см 2 ; DY = 6 °С; tзап = 2 мин
| t, мин | ||||||||
| DY | 0,3 | 0,9 | 3,2 | 3,9 | 4,4 | 4,8 | 5,1 | 5,3 |
| t, мин | ||||||||
| DY | 5,5 | 5,7 | 5,8 | 5,85 | 5,9 | 5,93 | 5,97 | 5,99 |
Задание № 14. DX = 0,15 кг/см 2 ; DY = 3,8 т/ч; tзап = 3 мин
| t, мин | |||||||||||||
| DY | 0,65 | 2,23 | 2,85 | 3,2 | 3,4 | 3,53 | 3,62 | 3,67 | 3,72 | 3,75 | 3,77 | 3,79 | 3,8 |
Задание № 15. DX = 0,2 кг/см 2 ; DY = 22,6 °С; tзап = 30 с
| t, мин | |||||||
| DY | 2,2 | 9,2 | 11,6 | 13,8 | 15,7 | 17,5 | |
| t, мин | |||||||
| DY | 19,1 | 20,4 | 21,3 | 21,9 | 22,3 | 22,5 | 22,6 |
Задание № 16. DX = 0,1 кг/см 2 ; DY = 5,5 °С; tзап = 0,55 мин
| t, мин | ||||||||||||
| DY | 0,133 | 0,7 | 2,2 | 3,733 | 4,62 | 5,0 | 5,23 | 5,34 | 5,4 | 5,43 | 5,47 | 5,5 |
Задание № 17. DX = 0,3 кг/см 2 ; DY = 6,5 °С; tзап = 1 мин
| t, мин | |||||||||||
| DY | 0,5 | 1,6 | 3,0 | 4,3 | 5,2 | 5,6 | 6,0 | 6,2 | 6,35 | 6,45 | 6,5 |
Приложение Г
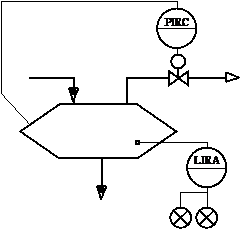
Практические задания по теме «Разработка функциональных схем автоматизации»
Общее задание
По заданной упрощенной функциональной схеме автоматизации построить полную схему, выбрать средства автоматизации с учетом указанных технологических параметров.
Результаты оформляются в виде расчетно-графической работы на листах формата А4, включающей чертеж схемы, спецификацию и краткое описание выбранных приборов.
На схемах обозначены Dу — диаметр трубопровода для подбора клапанов и диафрагм; DР — перепад давления на сужающем устройстве, См — смеситель.
Варианты заданий
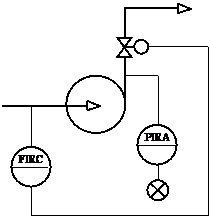
Вариант 1. Рисунок Г.1, а. Т = 70 ± 3 °С, L = 1,5 ± 0,5 м, Тmin = 40 °С,
Dу = 50 мм, Р = 0,6 МПа.
Вариант 2. Рисунок Г.1, б. Р = 0,12 ± 0,005 МПа, Pmax = 0,14 МПа,
Т = 185 ± 5 °С, Dу = 100 мм.
Вариант 3. Рисунок Г.1, в. Т = 250 ± 5 °С, L = 1,8 ± 0,3 м, Тmax = 270 °С,
Вариант 4. Рисунок Г.1,г. Т = 170 ± 3 °С, F = 50 ± 0,5 м 3 /ч,
Тmax = 180 °С, Тmin = 150 °С, Dу = 100 мм, Р = 0,5 МПа, DР = 6 МПа.
Вариант 5. Рисунок Г.1, д. Р = 0,8 ± 0,01 МПа, L = 1,0 ± 0,2 м, Lmin = 50 %L, Lmax = 80 %L, Dу = 50 мм, T = 50 °C.
Вариант 6. Рисунок Г.1,е. Т = 350 ± 8 °С, L = 1,5 ± 0,4 м, Lmin = 40 %L,
Lmax = 70 %L, Dу = 100 мм, Р = 0,3 МПа.
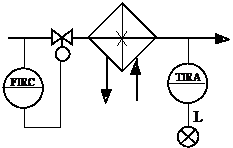
Вариант 7. Рисунок Г.2, а. P = 0,2 ± 0,001 МПа, Pmin = 0,19 МПа, Dу = 100 мм, Т1 = 40 ± 1 °С, Т2 = 45 ± 1 °С, Т3 = 50 ± 1 °С, Т4 = 55 ± 1 °С,
Вариант 8. Рисунок Г.2, б. FT = 20 ± 0,8 м 3 /час, DР = 0,3 КПа,
РТ = 0,11 МПа, DуТ = 50 мм, FВ = 150 ± 0,9 м 3 /час, DР = 0,3 КПа,
DуВ = 100 мм, Т = 750 ± 10 °С.
Вариант 9. Рисунок Г.2, в. Т = 20 °С, F = 200 ± 20 м 3 /час, Рmin = 2,3 КПа,
Dу = 200 мм, Р = 2,4 ± 0,1 МПа, DР = 6,3 КПа.
Вариант 10. Рисунок Г.2, г. Т = 300 ± 20 °С, F = 140 м 3 /ч, Fmin = 125 м 3 /ч,
Dу = 50 мм, Р = 5 МПа, DР = 10000 Па.
Вариант 11. Рисунок Г.2,д. Т = 850 ± 20 °С, FТ = 50 ± 0,5 м 3 /ч,
Тmax = 900 °С, Dу = 50 мм, Р = 0,15 МПа, DР = 10 КПа.
Вариант 12. Рисунок Г.2, е. Т = 350 ± 15 °С, L = 1,0 ± 0,2 м,
Lmin = 40 %L, Dу = 50 мм, Р = 0,11 МПа
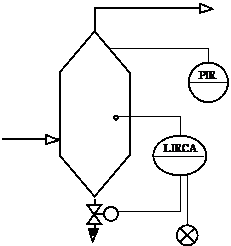
Вариант 13. Рисунок Г.3,а. Т = 350 ± 10 °С, F = 180 ± 5 м 3 /ч,
Тmin = 330 °С, Тmax = 370 °С, Dу = 150 мм, Р = 2,5 МПа, DР = 10 КПа.
Вариант 14. Рисунок Г.3, б. F = 100 ± 5 м 3 /ч, Fmax = 110 м 3 /ч,
Dу = 100 мм, Р = 0,1 ± 0,01 МПа, DР = 630 Па.
Вариант 15. Рисунок Г.3,в. Т = 80 ± 5 °С, Тmax = 100 °С, Dу = 200 мм,
Р = 0,8 ± 0,08 МПа, Рmin = 0,6 КПа.
Вариант 16. Рисунок Г.3,г. Т = 210 ± 5 °С, F = 200 ± 10 м 3 /ч, Тmin = 180 °С, Dу = 250 мм, Р = 0,5 МПа, DР = 6,3 КПа.
Вариант 17. Рисунок Г.3,д. Т = 40 °С, Р = 0,8 ± 0,004 МПа, Рmin = 0,75 КПа,
Dу = 100 мм, F = 120 м 3 /ч, DР = 10 КПа.
Вариант 18. Рисунок Г.3,е. F = 250 ± 10 м 3 /ч, Fmin = 230 м 3 /ч,
Dу = 200 мм, Р = 0,15 ± 0,001 МПа, DР = 1 КПа.
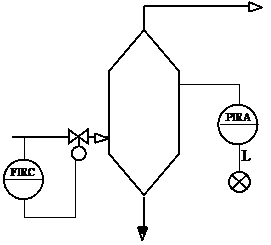
Вариант 19. Рисунок Г.4,а. F = 60 ± 3 м 3 /ч, Fmax = 63 м 3 /ч, Dу = 50 мм,
Р = 4 ± 0,5 МПа, DР = 6,3 КПа.
Вариант 20. Рисунок Г.4,б. Т = 240 °С, L = 1,2 ± 0,1 м, Lmax = 0,8 L,
Dу = 100 мм, Р = 0,6 ± 0,01 МПа,
Вариант 21. Рисунок Г.4,в. Т = 80 ± 5 °С, FА = 40 ± 0,5 м 3 /ч,
FБ = 40 ± 0,5 м 3 /ч, Тmax = 85 °С, DуА = DуБ = 50 мм, Р = 0,1 МПа.
Вариант 22. Рисунок Г.4,г. Т = 210 ± 10 °С, Рmin = 0,75 КПа, Dу = 100 мм,
Вариант 23. Рисунок Г.4,д. Р = 2 МПа, F = 140 ± 10 м 3 /ч, Тmin = 330 °С,
Dу = 100 мм, Dу.топл. = 50 мм, Т = 350 ± 10 °С, DР = 10 КПа.
Вариант 24. Рисунок Г.4,е. Т = 150 °С, F = 70 ± 0,5 м 3 /ч, Рmin = 1,4 МПа,
Dу = 50 мм, Р = 1,5 ± 0,2 МПа, DР = 0,4 КПа.
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |

 |
 |
 |
 |
 |

 |
- Передаточная функция САР
- Передаточная функция САР
- 2. Математическое описание систем автоматического управления ч. 2.9 — 2.13
- 2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)
- Пример
- 2.10. Весовая и переходная функции звена (системы).
- 2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона
- 2.12. Mетод переменных состояния.
- Пример решения задачи в форме коши.
- 2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно
- 2.13.1. Правая часть содержит только b0*u(t)
- 2.13.2. Правая часть общего вида
- Пример:
- 📸 Видео
Видео:Построить структурную схему САР (САУ) по передаточной функцииСкачать

Передаточная функция САР
Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Передаточная функция САР
Любое звено автоматической системы предназначено для измерения, усиления или какого-либо другого преобразования сигналов. В связи с этим для любого звена и всей системы в целом характерной является связь между входным и выходным сигналами или между входной и выходной величинами. В теории автоматического регулирования широкое применение получил способ математического описания, основанный на использовании передаточной функции.
Понятие передаточной функции. Звено или автоматическую систему в целом можно представить в виде плотно сбитого черного ящика, на одной из стенок которого смонтировано штепсельное гнездо с надписью «ВХОД«, а на другой — с надписью «ВЫХОД» откуда получаем новый сигнал — продукт переработки введенного сигнала. Как же судить о способностях такого преобразователя. Остается одно — сидеть около этого ящика и смотреть, каким сигнал входит в ящик и каким выходит, запоминать увиденное, обобщать, а потом уж предсказывать.
Вокруг нас в изобилии рассеяны объекты, несущественно отличающиеся от рассмотренного преобразователя. Это отличие может выразиться лишь в том, что поступающий сигнал имеет не электрическую, а механическую природу, или гидромеханическую, или термическую, или акустическую. Это может быть радиосигнал, оптический сигнал, сигнал химической природы и т. д. Преобразованию может подвергаться не только природа сигнала, но и величина его, как функция времени, знак и другие характеристики.
Преобразованию может подвергаться не только природа сигнала, но и его величина как функция времени, знак и другие характеристики. Однако слово «ящик» здесь применяется как символ ограниченности той части пространства, в которой происходит преобразование одного сигнала в другой.
Изучать черные ящики надо не потому, что их много, а потому, что это полезно. То что их много и что они разнообразны, вызывает лишь необходимость изучения их в общем виде, на модели, обладающей характерными чертами, общими для большой группы объектов, независимо от того какая их природа. Можно предполагать, что сравнивая входные и выходные сигналы мы всякий раз будем отмечать, что одинаковые входные сигналы для определенной группы преобразователей будут вызывать одинаковые выходные.
Закон, согласно которому производится преобразование сигналов внутри звена или автоматической системы, называется передаточной функцией.
Передаточная функция определяется только внутренними свойствами автоматической системы и является функцией комплексного переменного.
Передаточная функция характеризует динамические свойства звена или автоматической системы в целом только по определенному каналу, связывающему конкретный вход объекта регулирования и его конкретный выход.
Если объект регулирования имеет несколько входов и выходов, то он характеризуется несколькими передаточными функциями.
Понятие передаточной функции весьма удобно при анализе структурных схем. Передаточные функции звеньев или отдельных участков схемы автоматической системы позволяют легко получить общее уравнение всей автоматической системы, а в дальнейшем в случае необходимости перейти к исходному дифференциальному уравнению.
Описание передаточной функции. В теории автоматического регулирования широкое применение получил способ математического описания, основанный на использовании передаточной функции.
Формально передаточная функция получается из дифференциального уравнения автоматической системы после замены в нем символа кратного дифференцирования на соответствующую степень р и деления образованного таким образом многочлена правой части на многочлен левой части уравнения.
Как уже отмечалось, физические процессы в системе автоматического регулирования в общем случае описываются уравнением
Исключая из полученных уравнений промежуточные величины, можно найти уравнения относительно интересующих нас переменных. Но, как правило, эти операции очень трудоемки и громоздки. Поэтому возникает потребность как-то упростить эти промежуточные операции. Это может быть достигнуто, если вместо рассмотрения величин, характеризующих состояние автоматической системы во времени — оригиналов, рассматривать соответствующие им изображения, получаемые на основе преобразования Лапласа.
Предположим, что x(t) удовлетворяет условиям x(t) = 0; t
Видео:Дифференциальные уравнения. 11 класс.Скачать

2. Математическое описание систем автоматического управления ч. 2.9 — 2.13
Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.
Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.
В предыдущих сериях:
В это части будут рассмотрены:
2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена).
2.10. Весовая и переходная функции звена (системы).
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции.
2.12. Mетод переменных состояния.
2.13. Переход от описания переменных «вход-выход» к переменным состояния.
Попробуем применить, полученные знания на практике, создавая и сравнивая расчетные модели в разных видах. Будет интересно познавательно и жестко.
2.9. Использование обратных преобразований Лапласа для решения уравнений динамики САР (звена)
Рассмотрим динамическое звено САР изображенное на рисунке 2.9.1
Предположим, что уравнение динамики имеет вид:
где: — постоянные времени;
— коэффициент усиления.
Пусть известны отображения:
Найдем изображения для производных:
Подставим полученные выражения в уравнение динамики и получим уравнение динамики в изображениях:
B(s) — слагаемое, которое определяется начальными условиями, при нулевых начальных условиях B(s)=0.
W(s) — передаточная функция.
Передаточной функцией САР (звена) называется отношение изображений выходного сигнала к входному воздействию при нулевых н.у.
После того, как в явном виде найдено изображение для неизвестной выходной величины, нахождение оригинала не представляет сложностей. Либо по формуле Хэвисайда, либо разложением на элементарные дроби, либо по таблице из справочника.
Пример
Построить выходной сигнал звена САР при единичном входном воздействии и нулевых начальных условиях, если уравнение динамики звена имеет следующий вид:
входное воздействие: — единичное ступенчатое воздействие.
Выполним преобразование Лапласа:
Подставим в уравнение динамики и получим уравнение динамики в изображениях:
Для получения выходного сигнала из уравнения в изображениях выполним обратное преобразования Лапласа:
2.10. Весовая и переходная функции звена (системы).
Определение: Весовой функцией звена (системы) называется реакция системы при нулевых н.у. на единичное импульсное воздействие.
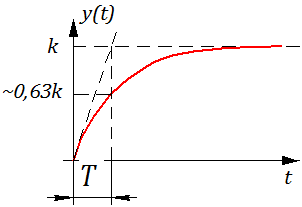
Определение: Переходной функцией звена (системы) при н.у. называется реакция на единичное ступенчатое воздействие.
На этом месте можно вспомнить, что преобразование Лапласа это интеграл от 0 до бесконечности по времени (см. предыдущий текст), а импульсное воздействие при таком интегрировании превращается в 1 тогда в изображениях получаем что:
Передаточная функция играет роль изображения реакции звена или системы на единичное импульсное воздействие.
Для единичного ступенчатого воздействия преобразование Лапласа тоже известно (см. предыдущий текст):
тогда в изображениях получаем, что реакция системы на ступенчатое воздействие, рассчитывается так:
Реакция системы на единичное ступенчатое воздействие рассчитывается обратным преобразованием Лапласа:
2.11. Определение переходного процесса в системе (САР) (звене) через весовую и переходную функции. Формула Дюамеля-Карсона
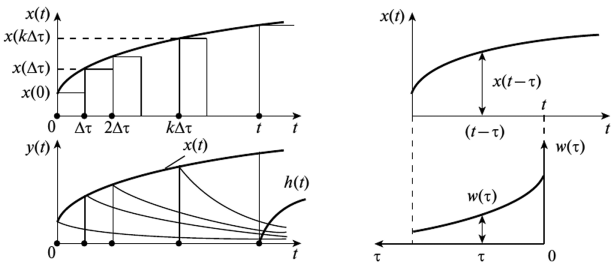
Предположим, что на вход системы поступает произвольное воздействие x(t), заранее известное. Найти реакцию системы y(t), если известны входное воздействие x(t) и весовая функция w(t).
Представим, что входное воздействие представляет собой последовательность прямоугольных импульсов до времени t и ступеньки высотой x(t) в момент времени t. см.рис. 2.11 Для каждого импульса мы можем записать реакцию системы через весовую функциию:
где:
— значение отклика по завершению предыущего импульса;
— время завершения текущего импульса;
— значение весовой функции в начале текущего импульса.
Тогда для определения занчения отклика в произвольный момент времени необходимо сложить все импульсы и ступенчатое воздействие в момент времени t:
Переходя к пределам
если перейти от t к бесконечности мы получим формулу интеграла Дюамеля-Карсона, или по другому «интеграла свертки» который обеспечивает вычисление оригинала функции по произвдению изображения двух функций:
где — вспомогательное время
Для вывода аналогичной зависмости от переходной функции вспомним что изображение весовой и переходной функции связаны соотношением: запишем выражение изображения для отклика в операторной форме:
Используя интеграл свертки получаем, что при известной переходной функции (h(t)) и известному входному воздействию х(t) выходное воздействие рассчитывается как:
2.12. Mетод переменных состояния.
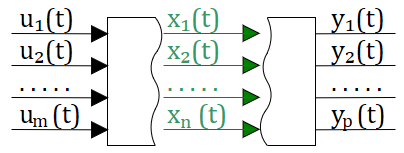
До этого мы рассматривали системы с одной передаточной функцией, но жизнь всегда сложнее и как правило в системах есть несколько передаточных функций несколько входных воздейстий и несколько реакций системы. (см. рис. 2.12.1)
В этом случае наиболее удобной формой пердставления систем для их анализа и расчета оказался метод переменных состояния. Для этого метода, вместо передаточных функций связывающих вход с выходом используются дополнительные переменные состояния, которые описывают систему. В этом случае можно говорить, что состояние системы — это та минимальная информация о прошлом, которая необходима для полного описания будущего поведения (т.е. выходов) системы, если поведение ее входов известно. см. рис. 2.12.2
В методе состояний, производные всех переменных состояния, в общем случае зависит от всех переменных и всех входных воздействия, и могут быть записаны в представленной ниже системы обыкновенных дифференциальных уравнений (ОДУ) первой степени. Эта система уравнений называю системой ОДУ в форме Коши:
Выход из системы зависит от переменных состояния и, в общем случае от входных воздействий и описывается следующей системой уравнений:
где:
n — количество перемнных состояния,
m — количество входных воздействий,
p — количество выходных переменных;
Данная система уравнений может быть записана в матричной форме:
где:
— вектор входа (или вектор управления);
— вектор столбец производных переменных состояния;
— вектор столбец переменных состояния;
— вектор выхода;
— собственная матрица системы [n x n],
— постоянные коэффициенты;
— матрица входа [n x m],
— постоянные коэффициенты;
— матрица выхода а [p x n],
— постоянные коэффициенты;
— матрица обхода [p x m],
— постоянные коэффициенты;
В нашем случае почти всегда все элементы матрицы D будут нулевыми: D = 0.
Такое описание системы позволяет с одной стороны стандартным образом описывать различные технические системы. Явная формула для расчета производных позволяет достаточно просто осуществлять численное интегрирование по времени. И это используется в различных программах моделирования
Другое использование данного представления для простых систем, описанных в переменных «вход-выход», зачастую позволяет устранить технические трудности, связанные с решением ОДУ высокой степени.
Еще одним преимуществом данного описания, является то, что уравнения в форме Коши можно получить из законов физики
Пример решения задачи в форме коши.
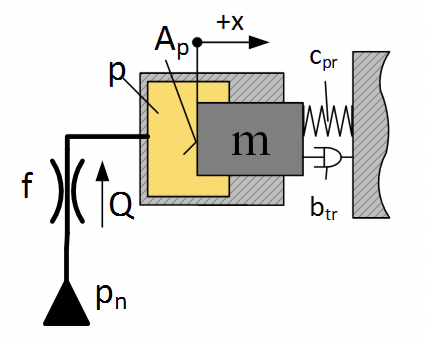
Рассмотрим задачу моделирования гидравлического привода, при следующих условиях:
Дано:
Цилиндрический плунжер диаметром 10 мм, с приведенной массой 100 кг, работает на пружину жесткостью 200 Н/мм и демпфер с коэффициентом вязкого трения — 1000 Н/(м/с). Полость начальным объемом 20 см 3 соединяется с источником давлния дросселем диаметром диаметр которого 0,2 мм. Коэффициент расхода дросселя 0.62. Плотность рабочей жидкости ρ = 850 кг/м 3 .
Определить:
Перемещение дросселя, если в источнике давление происходит скачек 200 бар. см. рис. 2.12.13
Уравенение движение плунжера:
Где: – площадь плунжера,
– жесткость пружины,
– коэффициент вязкого трения, p – давление в камере.
Поскольку дифференциальное движения это уравнение второго порядка, превратим его в систему из двух уравнений первого порядка, добавив новую переменную — скорость , тогда
Уравнение давления в камере, для упрощения принимаем что изменениям объема камеры из-за перемещения плунжера можно пренебречь:
Где: Q – расход в камеру, V — объем камеры.
Расход через дроссель:
Где: f– площадь дросселя, – давление в источнике, p – давление в камере.
Уравнение дросселя не линейное, по условию задачи, давление входное изменяется скачком, от 0 до 200 бар, проведем линеаризацию в окрестности точки давления 100 бар тогда:
Подставляем линеаризованную формул расхода в формулу давления:
Таким образом общая система уравнений в форме Коши, для рис 2.12.3 привода принимает вид:
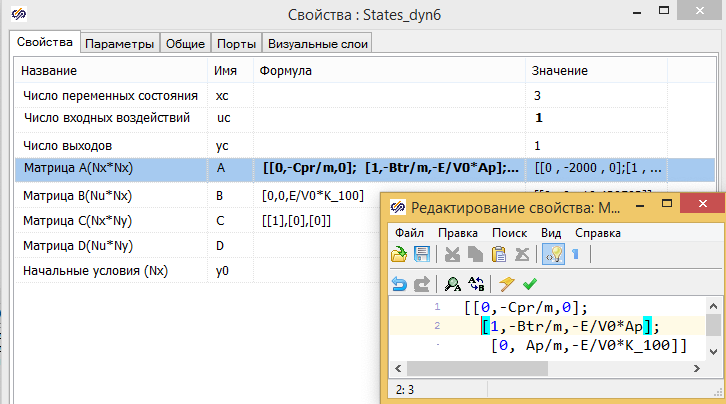
Матрицы A, B, С, В для матричной формы системы уравнений принимают вид:
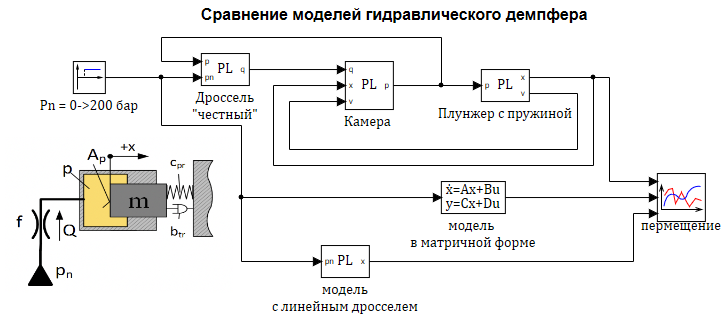
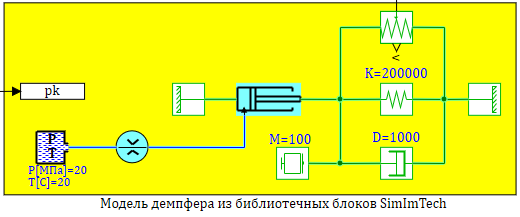
Проверим моделированием в SimInTech составленную модель. На рисунке 2.12.13 представлена расчетная схема содержащая три модели:
1 — «Честная» модель со всеми уравнениями без упрощений.
2 — Модель в блоке «Переменные состояние» (в матричной форме).
3 — Модель в динамическом блоке с линеаризованным дросселем.
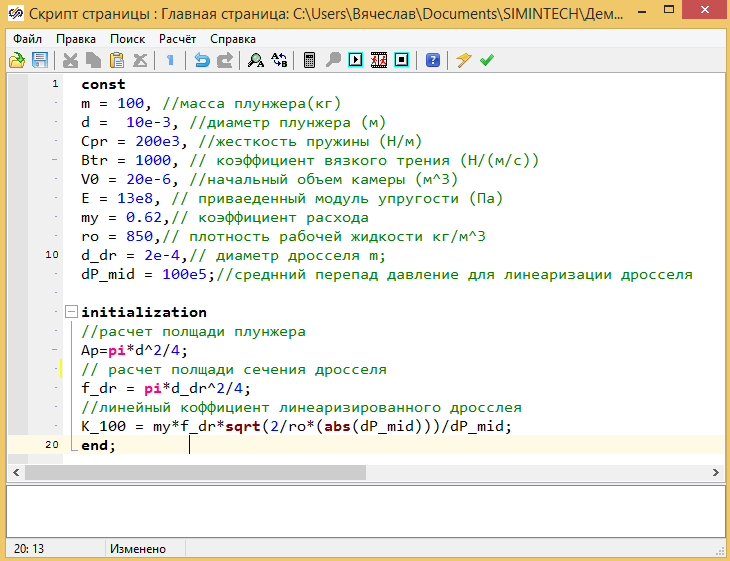
Все условия задачи задаются как глобальные константы проекта, в главном скрипте проекта, там же расчитываются на этапе инициализации расчета, площади плунжера и проходного сечения дросселя см. рис. 2.12.5:
Рисунок 2.12.5 Глобальный скрипт проекта.
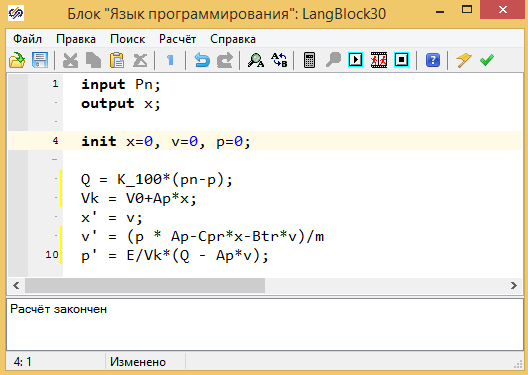
Модель на внутреннем языке программирования представлена на рис. 2.12.6. В данной модели используется описание модели в форме Коши. Так же выполняется учет изменения объема дросселя на каждом шаге расчета, за счет перемещения плунжера (Vk = V0+Ap*x.)
Рисунок 2.12.6 Скрипт расчета модели в форме Коши.
Модель в матричном форме задается с использованием глобальных констант в виде формул. (Матрица в SimInTech задается в виде последовательности из ее столбцов) см. рис. 2.12.7
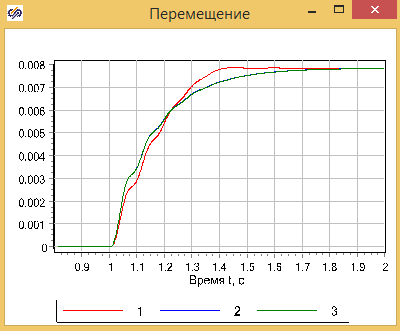
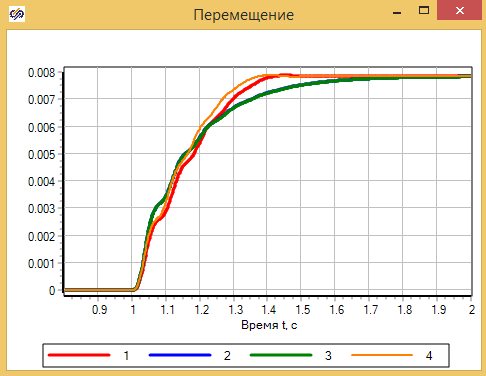
Результаты расчета показывают, что модель в матричной форме и модель на скриптовом языке в форме Коши, практически полностью совпадают, это означает, что учет изменения объема полости практически не влияют на результаты. Кривые 2 и З совпадают.
Процедура линеаризация расхода через дроссель вызывает заметное отличие в результатах. 1-й график c «честной» моделью дросселя, отличается от графиков 2 и 3. (см. рис. 2.12.8)
Сравним полученные модели, с моделью созданной из библиотечных блоков SimInTech, в которых учитываются так же изменение свойств реальной рабочей жидкости — масла АМГ-10. Сама модель представлена на рис. 2.12.9, набор графиков на рисунке 2.12.10
На графиках видно, что уточненная модель отличается от предыдущих, однако погрешность модели составлят наших упрощенных моделей составляют примерно 10%, в лишь в некоторые моменты времени.
2.13. Переход от описания переменных «вход-выход» к переменным состояния и обратно
Рассмотрим несколько вариантов перехода от описания «вход-выход», к переменным состояния:
Вариант прехода зависит от правой части уравнения с переменными «вход-выход»:
2.13.1. Правая часть содержит только b0*u(t)
В этом варианте, в уравнениях в правой части отсутствуют члены с производными входной величины u(t). Пример с плунжером выше так же относится к этому варианту.
Что бы продемонстрировать технологию перехода рассмотрим следующее уровнение:
Для перехода к форме Коши ведем новые переменные:
И перепишем уравнение относительно y»'(t):
Используя эти переменные можно перейти от дифференциального уравнения 3-го прядка, к системе из 3-х уравнений первого порядка в форме Коши:
Соотвественно матрицы для матричного вида уравнений в переменных сосотяния:
2.13.2. Правая часть общего вида
Более сложный случай, когда в уравнениях есть производные от входных воздействий и уравнение в общем случае выглядит так:
Сделаем преобразования: перейдем к уравнениям динамики в изображениях:
Тогда можно представить уравнение в изображениях в виде:
Разделим уравнение в изображениях на произведение полиномов , получим:
Где: — некоторая комплексная величина (отношение двух комплексных величин). Можно считать, что
отображение величины
. Тогда входная величина может быть в изображениях представлена как:
Вренемся к оригиналу от изображений получим: ,
где: — дифференциальный оператор.
А это дифференциальное уравнение n-го порядка мы можем преобразовать к системе из n дифференциальных уравнений первого порядка, как это мы делали выше:
Таким образом, мы получили систему уравнение в форе Коши, относительно переменных состояния :
А регулируемую величину (выход системы) мы так же можем выразить через эти переменные, в изображениях:
Перейдем от изображения к оригиналам:
Если обозначить вектор , то мы получим уравнения переменных состояниях в матричной форме, где D = 0:
Пример:
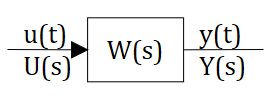
Рисунок 2.13.1 Передаточная функция.
Имеется передаточная функция (рис. 2.13.1) в изображениях :
Необходимо преобразовать передаточную функцию к системе уравнений в форме Коши
В изображения реакция системы связана с входным воздействие соотношением:
Разделим в последнем правую и левую часть на произведения , и введем новую перменную
:
Полиномы N(s) и L(s) равны:
Перейдем в последнем выражении от изображения к оригиналам и ведем новые переменные (состояния):
Переходим от уравнения третьего порядка к системе трех уравнений первого порядка:
Или в матричной форме:
Для получения второго матричного уравнения воспользуемся соотношением для новых переменных в отображениях:
Перейдем от изображений к оригиналу:
Таким образом второе уравнение матричной системы выглядит так:
Проверим в SimInTech сравнив передаточную функцию и блок переменных состояния, и убедимся, что графики совпадают см. рис. 2.13.2
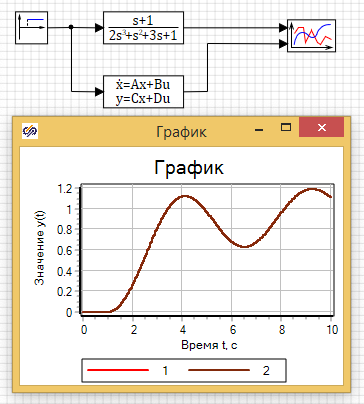
Рисунок 2.13.2 Сравнение переходного процеса у блока передаточной функции и блока переменных состояния.
📸 Видео
2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать

13. Как решить дифференциальное уравнение первого порядка?Скачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

ДУ Уравнения, не разрешенные относительно производнойСкачать

✓Дифференцируемая функция. Дифференциал | матан #032 | Борис ТрушинСкачать

1. Что такое дифференциальное уравнение?Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Видеометодичка. Практикум по нахождению передаточных функций по дифференциальным уравнениямСкачать

Метод пространства состояний САУ: описание конкретной системыСкачать

11. Уравнения в полных дифференциалахСкачать

Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Дифференциал функцииСкачать

Составить дифференциальные уравнения семейств линийСкачать

Частное решение дифференциального уравнения. 11 класс.Скачать