 | Пусть дана точка 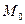 с координатами с координатами  и направляющий вектор и направляющий вектор  (выделен жирно на чертеже) Представим себе, что какая-то произвольная точка (выделен жирно на чертеже) Представим себе, что какая-то произвольная точка  с координатами с координатами  лежит на этой же прямой. Тогда лежит на этой же прямой. Тогда  и и  коллинеарны, то есть их координаты — пропорциональны, т.е. коллинеарны, то есть их координаты — пропорциональны, т.е.  |
тогда 
Это канонические уравнения прямой в пространстве.
Фактически здесь не одно, а два уравнения, впрочем, это прямая может быть задана как пересечение 2 плоскостей. Кстати, если перемножить 1-ю и 2-ю пропорции независимо друг от друга, и свести к обычным уравнениям, то мы и получили бы уравнения каких-то 2 плоскостей.
Если эти 3 дроби равны, то можно приравнять их к некоторому параметру t.



Векторный вид записи этих 3 равенств: 

Пример. Построить уравнения прямой, если начальная точка (1,1,1) направляющий вектор (1,2,3).

тогда 
Параметрические:
Если привести 2 пропорции 




это и есть уравнения двух плоскостей, в пересечении который лежит эта прямая.
Замечание. Если требуется построить уравнение прямой по 2 точкам, то направляющий вектор от 1-й ко 2-й точке, и далее известный алгоритим.
Пункт 2. Построение уравнения прямой в пространстве по точке и двум перпендикулярам.
Если дана точка и 2 нормали, то можно найти направляющий как векторное произведение этих 2 нормалей:

Замечание. Кстати, канонические уравнения существуют не всегда, а вот параметрические — более универсальны, они существуют всегда, даже если направляющий лежит параллельно какой-то оси. А для канонических уравнений при этом получался бы 0 в знаменателе. Пример, показывающий данную ситуацию:
Пример. Если 2 перпендикуляра (1,0,0) и (1,1,0) то их векторное произведение (0,0,1) — направляющий.
Параметрические уравнения: x = 0 , y = 0 , z = t.
Пункт 3. Расстояние от точки до прямой в пространстве.
Во-первых, закономерен вопрос, а почему требуется выводить новую формулу, если у нас уже была выведена формула расстояния от точки до прямой? Дело в том, что в пространстве уравнение прямой это вовсе не 
Пусть дана прямая (с помощью точки 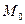

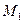
 | Соединим 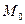 и и 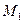 , это одна из двух сторон параллелограмма, вторая это , это одна из двух сторон параллелограмма, вторая это  . Требуемое расстояние это высота, надо площадь поделить на длину основания. Площадь равна векторному произведению векторов, образующих стороны. Поэтому . Требуемое расстояние это высота, надо площадь поделить на длину основания. Площадь равна векторному произведению векторов, образующих стороны. Поэтому  . . |
Пункт 4. Взаимное расположение прямых в пространстве.
Кроме совпадения, параллельности и пересечения, в пространстве появляется ещё одна ситуация: скрещивающиеся прямые.
Скрещивающиеся прямые можно определить как две прямые, не лежащие в одной плоскости. Через совпадающие, пареллельные, пересекающиеся прямые можно провести общую плоскость. Скрещивающиеся прямые можно представить себе как пару прямых, лежащих в параллельных плоскостях, но при этом сами прямые не параллельны (если рассмотреть вид сверху, то они пересекались бы).
| Если | и при этом: | тогда прямые: |
 |  | Совпадающие |
 | Параллельные | |
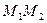  и и  компланарны (в одной плоскости) компланарны (в одной плоскости) | Пересекающиеся | |
 | Скрещивающиеся |
Примером отрезков, лежащих на скрещивающихся прямых, могут быть, например, мост и русло реки. Из-за того, что в пространстве возможны скрещивающиеся прямые, как раз и есть возможность строительства мостов и развязок.
- Практика. Решение задач. Часть 1. Уравнения прямой
- Уравнение прямой
- Уравнение прямой на плоскости
- Уравнение прямой с угловым коэффициентом
- Уравнение прямой в отрезках на осях
- Уравнение прямой, проходящей через две различные точки на плоскости
- Параметрическое уравнение прямой на плоскости
- Каноническое уравнение прямой на плоскости
- Уравнение прямой в пространстве
- Уравнение прямой, проходящей через две различные точки в пространстве
- Параметрическое уравнение прямой в пространстве
- Каноническое уравнение прямой в пространстве
- Прямая как линия пересечения двух плоскостей
- 💥 Видео
Видео:Геометрия. 9 класс. Уравнение прямой. Направляющий вектор и вектор нормали прямой /22.10.2020/Скачать

Практика. Решение задач. Часть 1. Уравнения прямой
Этот видеоурок доступен по абонементу
У вас уже есть абонемент? Войти
Мы изучили новые инструменты – координаты и действия с векторами в координатах, операцию скалярного умножения векторов. Этот урок мы посвятим решению задач и потренируемся применять эти новые инструменты на практике.
Видео:Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Уравнение прямой
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
| x | + | y | = 1 |
| a | b |
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x — x 1 | = | y — y 1 |
| x 2 — x 1 | y 2 — y 1 |
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) — координаты точки лежащей на прямой, a = — координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a = ( l и m не равны нулю), то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x — x 0 | = | y — y 0 |
| l | m |
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x — 1 2 — 1 = y — 7 3 — 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x — x 1 | = | y — y 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
 | x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) — координаты точки лежащей на прямой, — координаты направляющего вектора прямой.
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n = , то уравнение прямой можно записать в каноническом виде, используя следующую формулу
| x — x 0 | = | y — y 0 | = | z — z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
💥 Видео
Составляем уравнение прямой по точкамСкачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Как составить уравнение прямой, проходящей через две точки на плоскости | МатематикаСкачать

Видеоурок "Канонические уравнения прямой"Скачать

Видеоурок "Нормальное уравнение прямой"Скачать

Видеоурок "Общие уравнения прямой"Скачать

Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

1. Уравнение плоскости проходящей через точку перпендикулярно вектору / общее уравнение / примерыСкачать

Построение угла, равного данному. 7 класс.Скачать

Написать канонические и параметрические уравнения прямой в пространствеСкачать

18+ Математика без Ху!ни. Скалярное произведение векторов. Угол между векторами.Скачать

9 класс, 6 урок, Уравнение окружностиСкачать

Уравнения прямой на плоскости | Векторная алгебраСкачать

11. Прямая в пространстве и ее уравненияСкачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать







