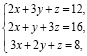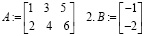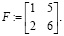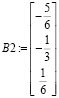//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
- Калькулятор онлайн. Решение системы двух линейных уравнений с двумя переменными. Метод подстановки и сложения.
- Немного теории.
- Решение систем линейных уравнений. Способ подстановки
- Решение систем линейных уравнений способом сложения
- Как можно решить систему уравнений в mathcad
- Решение системы уравнений с помощью математического пакета.
- Решение системы уравнений матричным способом в среде MathCAD
- Решение системы уравнений с помощью функции Given .. Find в среде MathCAD
- Решение системы уравнений с помощью функции Given .. Minerr в среде MathCAD.
- Создание базы данных «Расписание автобусов» с помощью пакета Access
- 2. Работа с массивами
- 1. Ранжированные переменные
- Рис. 1.1. Примеры использования ранжированных переменных
- 2. Работа с массивами
- Ранжированная переменная отличается от вектора (одномерного массива) тем, что невозможно использование ее отдельных значений. При необходимости иметь доступ к каждому значению переменной со многими компонентами она должна быть задана в виде одномерного (вектора) и двумерного (матрицы) массива.
- Как можно решить систему уравнений в mathcad
- Привет студент
- ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
- тема: «ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ»
- Дана система уравнений какая программа верно отражает решение данной системы уравнений
- Где учитесь?
- 🎦 Видео
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Калькулятор онлайн.
Решение системы двух линейных уравнений с двумя переменными.
Метод подстановки и сложения.
С помощью данной математической программы вы можете решить систему двух линейных уравнений с двумя переменными методом подстановки и методом сложения.
Программа не только даёт ответ задачи, но и приводит подробное решение с пояснениями шагов решения двумя способами: методом подстановки и методом сложения.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.
При вводе уравнений можно использовать скобки. При этом уравнения сначала упрощаются. Уравнения после упрощений должны быть линейными, т.е. вида ax+by+c=0 с точностью порядка следования элементов.
Например: 6x+1 = 5(x+y)+2
В уравнениях можно использовать не только целые, но также и дробные числа в виде десятичных и обыкновенных дробей.
Правила ввода десятичных дробей.
Целая и дробная часть в десятичных дробях может разделяться как точкой так и запятой.
Например: 2.1n + 3,5m = 55
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Примеры.
-1&2/3y + 5/3x = 55
2.1p + 55 = -2/7(3,5p — 2&1/8q)
Решить систему уравнений
Видео:Решение систем уравнений второго порядка. 8 класс.Скачать

Немного теории.
Видео:Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать

Решение систем линейных уравнений. Способ подстановки
Последовательность действий при решении системы линейных уравнений способом подстановки:
1) выражают из какого-нибудь уравнения системы одну переменную через другую;
2) подставляют в другое уравнение системы вместо этой переменной полученное выражение;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.
Пример. Решим систему уравнений:
$$ left< begin 3x+y=7 \ -5x+2y=3 end right. $$
Выразим из первого уравнения y через x: y = 7-3x. Подставив во второе уравнение вместо y выражение 7-Зx, получим систему:
$$ left< begin y = 7—3x \ -5x+2(7-3x)=3 end right. $$
Нетрудно показать, что первая и вторая системы имеют одни и те же решения. Во второй системе второе уравнение содержит только одну переменную. Решим это уравнение:
$$ -5x+2(7-3x)=3 Rightarrow -5x+14-6x=3 Rightarrow -11x=-11 Rightarrow x=1 $$
Подставив в равенство y=7-3x вместо x число 1, найдем соответствующее значение y:
$$ y=7-3 cdot 1 Rightarrow y=4 $$
Пара (1;4) — решение системы
Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными. Системы, не имеющие решений, также считают равносильными.
Видео:10 класс. Алгебра. Системы уравненийСкачать

Решение систем линейных уравнений способом сложения
Рассмотрим еще один способ решения систем линейных уравнений — способ сложения. При решении систем этим способом, как и при решении способом подстановки, мы переходим от данной системы к другой, равносильной ей системе, в которой одно из уравнений содержит только одну переменную.
Последовательность действий при решении системы линейных уравнений способом сложения:
1) умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) складывают почленно левые и правые части уравнений системы;
3) решают получившееся уравнение с одной переменной;
4) находят соответствующее значение второй переменной.
Пример. Решим систему уравнений:
$$ left< begin 2x+3y=-5 \ x-3y=38 end right. $$
В уравнениях этой системы коэффициенты при y являются противоположными числами. Сложив почленно левые и правые части уравнений, получим уравнение с одной переменной 3x=33. Заменим одно из уравнений системы, например первое, уравнением 3x=33. Получим систему
$$ left< begin 3x=33 \ x-3y=38 end right. $$
Из уравнения 3x=33 находим, что x=11. Подставив это значение x в уравнение ( x-3y=38 ) получим уравнение с переменной y: ( 11-3y=38 ). Решим это уравнение:
( -3y=27 Rightarrow y=-9 )
Таким образом мы нашли решение системмы уравнений способом сложения: ( x=11; y=-9 ) или ( (11; -9) )
Воспользовавшись тем, что в уравнениях системы коэффициенты при y являются противоположными числами, мы свели ее решение к решению равносильной системы (сумировав обе части каждого из уравнений исходной симтемы), в которой одно из уравнений содержит только одну переменную.
Видео:Решение системы уравнений методом обратной матрицы.Скачать

Как можно решить систему уравнений в mathcad
Видео:Матричный метод решения систем уравненийСкачать

Решение системы уравнений с помощью математического пакета.
Решение системы уравнений матричным способом в среде MathCAD
Матрицей называется прямоугольная таблица, элементы которой принадлежат некоторому множеству.
Дана система уравнений:
Составляем матрицы А и В. А — матрица данной системы уравнений. В — матрица: столбец для данной системы уравнений.
По правилам матричного исчисления получаем уравнение: А * х = В. х — матрица: столбец из неизвестных.
Решая это уравнение, найдем решение системы.
Решение системы уравнений с помощью функции Given .. Find в среде MathCAD
При решении систем не линейных уравнений используется специальный вычислительный блок, открываемый служебным словом-директивой Given.
Дана система уравнений:
Начальное условие определяет начальное значение искомых переменных, которые задаются путем обычного присваивания. Для многих уравнений берется произвольное начальное значение.
Записываем служебное слово-директиву Given и задаем уравнения системы с помощью жирного знака равенства между левой и правой частями каждого уравнения.
Записываем функцию Find. Она возвращает значение одной или ряда переменных для точного решения. Функция Find используется, если решение реально существует.
Таким образом х1 = -0.723;
Решение системы уравнений с помощью функции Given .. Minerr в среде MathCAD.
Дана система уравнений
Начальное условие определяет начальное значение искомых переменных, которые задаются путем обычного присваивания:
Записываем служебное слово-директиву Given и задаем уравнения системы с помощью жирного знака равенства:
Записываем функцию Minerr. Она возвращает значение одной или ряда переменных для приблизительного решения. Функция Minerr пытается найти максимально приближение даже к несуществующему решению путем минимизации средней квадратичной погрешности решения.
Таким образом х1 = -0.723;
Видео:10 класс. Алгебра. Системы уравненийСкачать

Создание базы данных «Расписание автобусов» с помощью пакета Access
База данных — это набор сведений, относящихся к определенной теме или задаче. БД является информационной моделью предметной области. Обращение к БД осуществляется с помощью систем управления базами данных (СУБД). СУБД Access является системой управления базами данных реляционного типа. Данные хранятся в такой базе в виде таблиц. С каждой таблицей могут быть связаны индексы (ключи), задающие нужные пользователю порядки на множестве строк. Таблицы могут иметь однотипные поля (столбцы), и это позволяет устанавливать между ними связи, выполнять операции реляционной алгебры.
Базы данных, как правило, обладают следующими признаками:
БД содержит некоторое множество данных, необходимых для решения конкретных задач многих пользователей (в том числе как реальных, так и потенциальных) или удовлетворения соответствующих информационных потребностей;
данные или информационные элементы в БД определенным образом структурированы и связаны между собой, при этом структура, состав данных и их содержание в БД не зависят от особенностей прикладных программ, используемых для управления БД;
данные представлены на машиночитаемых носителях в форме, пригодной для оперативного использования их с применением средств вычислительной техники, включая и системы управления базами данных.
Основные функции СУБД следующие:
Определение данных — определить, какая именно информация будет храниться в базе данных, задать свойства данных, их тип, а также указать, как эти данные связаны между собой.
Обработка данных — данные могут обрабатываться самыми различными способами. Можно выбирать любые поля, фильтровать и сортировать данные. Можно объединять данные с другой, связанной с ними, информацией и вычислять итоговые значения.
Управление данными — можно указать, кому разрешено знакомиться с данными, корректировать их или добавлять новую информацию.
Проектируя базу данных «Расписание автобусов», разбиваем ее на две связные таблицы. В первой таблице содержатся следующие поля: пункт назначения; время отправления; время в пути; количество посадочных мест. А во второй: время отправления; расстояние до пункта назначения.
При создании базы данных следует соблюдать следующие принцыпы:
· В каждой таблице не должно быть повторяющихся полей;
· В каждой таблице олжен быть уникальный идентификатор — ключ;
· Каждому значению первичного ключа должна соответствоватьдостаточная информация о сущности или объекте таблицы.
Создадим таблицы в режиме конструктора:
С тем чтобы Microsoft Access мог связать данные из разных таблиц каждая таблица должна содержать поле или набор полей, которые будут задавать индивидуальное значение каждой записи в таблице. Такое поле или набор полей называют основным ключом.
Видео:Решение системы уравнений методом ГауссаСкачать

2. Работа с массивами
Одна из задач ЭВМ — автоматизация труда, повышение эффективности научных исследований. Основная особенность ЭВМ — ориентация на применение пользователями, не владеющими языками программирования. Такой подход позволяет преодолевать языковой барьер, отделяющий человека от машины. С этой целью разрабатываются пакеты прикладных программ, рассчитанные на широкие круги специалистов. К подобным пакетам относится MATHCAD.
MATHCAD — универсальный математический пакет, предназначенный для выполнения инженерных и научных расчетов. Основное преимущество пакета — естественный математический язык, на котором формируются решаемые задачи.
Объединение текстового редактора с возможностью использования общепринятого математического языка позволяет пользователю получить готовый итоговый документ. Пакет обладает широкими графическими возможностями, расширяемыми от версии к версии. Практическое применение пакета существенно повышает эффективность интеллектуального труда.
Цель работы: изучение выполнения основных операций с массивами, решения систем линейных и нелинейных уравнений в Mathcad.
Видео:Решение систем уравнений. Подготовка к ЕГЭ и ОГЭСкачать

1. Ранжированные переменные
В математике часто возникает необходимость в задании некоторого ряда значений. Например, при вычислении 
Где Name – имя переменной, Nbegin – начальное значение переменной, Nend – ее конечное значение. Символ «…» (он вводится с клавиатуры знаком точка с запятой «;») указывает на изменение переменной в заданных границах. Если Nbegin <Nend,то шаг изменения переменной будет равен +1, в противном случае –1. Например, выражение a:=1…10 описывает ранжированную переменную a со значениями от 1 до 10.
Для создания ранжированной переменной общего вида используется выражение
где Step — заданный шаг изменения переменной (он должен быть положительным, если Nbegin <Nendи отрицательным в противном случае).
Например, выражение a:=1, 1.5, …10 описывает ранжированную переменную a со значениями от 1 до 10 с шагом 0,5.
Ранжированные переменные широко применяются для представления функций в виде таблиц вывода , а также для построения их графиков.
Если после некоторого выражения с ранжированной переменной поставить знак равенства, то после щелчка мышью на экране будет выведена таблица значений этого выражения. Такие таблицы называются таблицами вывода .
Необходимо учитывать следующее свойство таблиц вывода: если количество значений ранжированной переменной и, соответственно, строк в таблице вывода больше 16, то выводятся первые 16 строк. Если указатель мыши находится в пределах таблицы, то щелчок левой кнопкой мыши приводит к появлению вертикальной полосы прокрутки, позволяющей просмотреть все строки таблицы.
Помните, что задание ранжированных переменных эквивалентно заданию конечных циклов.
Примеры использования ранжированных переменных приведены на рисунке 1.1.
Видео:СИСТЕМЫ УРАВНЕНИЙ В ЕГЭ ЧАСТЬ I #shorts #математика #егэ #огэ #профильныйегэСкачать

Рис. 1.1. Примеры использования ранжированных переменных
Видео:Системы уравнений методы решения. Системы уравнений высших степеней.Скачать

2. Работа с массивами
Ранжированная переменная отличается от вектора (одномерного массива) тем, что невозможно использование ее отдельных значений. При необходимости иметь доступ к каждому значению переменной со многими компонентами она должна быть задана в виде одномерного (вектора) и двумерного (матрицы) массива.
Местоположение элемента массива задается одним индексом для вектора и двумя для матрицы. Индексы могут быть только положительными целыми числами . Для ввода индекса используется знак « [ » – прямая открывающая скобка.
Для задания массивов можно либо воспользоваться командой Matrices меню Math, либо нажать комбинацию клавиш Ctrl+V , либо щелкнуть на значке с изображением шаблона матрицы. Любое из этих действий вызывает появление диалогового окна, в котором надо указать количество строк m и столбцов n в массиве. При m=1 получим вектор-столбец, а при n=1 – вектор-строку.
В отношении массивов действуют те же правила присваивания и вывода, что и для обычных переменных. В частности, с помощью оператора присваивания можно создать массив заданного размера и заданного типа без ручного заполнения шаблона (рисунок 2.1.).
Рис. 2.1 Пример создания матриц без использования шаблонов матриц
Для работы с массивами Mathcad содержит ряд операторов и функций. Ниже представлены операторы для работы с векторами и матрицами. В таблице используются следующие обозначения: V – для векторов, M – для матриц, Z – для скалярных величин.
Видео:Решение системы уравнений методом обратной матрицы - bezbotvyСкачать

Как можно решить систему уравнений в mathcad
Линейное алгебраическое уравнение можно определить как уравнение, в которое искомые неизвестные входят в первой степени и между собой не перемножаются, т.е. в левой части линейного уравнения обычно записывается линейная комбинация искомых неизвестных, а в правой – свободный член. Совокупность таких уравнений образует систему линейных алгебраических уравнений (СЛАУ). Если СЛАУ имеет единственное решение, то она называется определённой. В случаях, когда решений бесконечное множество, СЛАУ называется неопределённой. Для решения определенных СЛАУ применяют методы Крамера, Гаусса, матричный, численные методы. Для неопределённой СЛАУ можно находить общее решение и какие-либо частные решения из их бесконечного множества.
В соответствии с ФГОС раздел «Линейная алгебра» модуля «Математика 1» входит в рабочие программы всех унифицированных образовательных математических кластеров дисциплины «Математика» [1]. В рабочие программы в обязательном порядке включаются индивидуальные домашние задания (ИДЗ) по всем разделам, в том числе и по разделу «Линейная алгебра». Решение СЛАУ «вручную» требует много времени, большого внимания, довольно громоздких преобразований и вычислений. Если допущена ошибка в решении СЛАУ, её бывает нелегко обнаружить. Целью применения пакета Mathcad в учебном процессе явилась потребность использования возможностей компьютеров для решения СЛАУ.
Квадратные СЛАУ с невырожденной основной матрицей системы, а также матричные уравнения в среде пакета Mathcad легко решаются матричным методом. Например, чтобы решить СЛАУ
достаточно задать основную матрицу системы
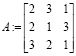
столбец свободных членов
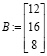
записав произведение обратной матрицы A –1 на матрицу В и воспользовавшись клавишей «=», получить решение:
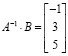
Проверка правильности решения также осуществляется в одно действие умножением матрицы А на найденную матрицу решения:
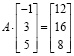
Можно предварительно записать найденную матрицу
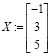
решения СЛАУ, тогда для проверки потребуется ввести с клавиатуры произведение 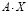
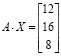
Начиная с шестой версии Mathcad, квадратные СЛАУ с невырожденной матрицей можно решать, используя встроенную функцию lsolve(A,B): X:= lsolve(A,B), и сразу получить решение
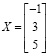
Для решения неопределенных СЛАУ в среде пакета Mathcad имеется несколько возможностей. Версия Mathcad 13/14 (в предыдущих версиях Mathcad основная матрица СЛАУ должна быть квадратной) позволяет находить одно из бесконечного множества частных решений СЛАУ при помощи встроенной функции lsolve(A,B) [2]. Например, так:
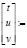
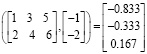
если решается СЛАУ
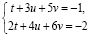
Замена знака равенства стрелкой из палитры символьных операций Symbolic возвращает частное решение в виде рациональных чисел:
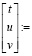
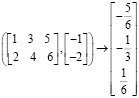
Но общее решение, применяя встроенную функцию lsolve(A,B), найти не удается.
Получить общее решение СЛАУ можно директивой solve палитры символьных операций Symbolic. Для этого надо в левую метку директивы solve записать матрицу из одного столбца и таким количеством строк, сколько уравнений в СЛАУ, отделяя свободные члены равенствами из палитры Boolean или вводя знаки «=» с клавиатуры вместе с клавишей Ctrl (получается «жирный» знак равенства). В правой метке следует перечислить имена всех неизвестных СЛАУ. Например,
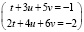
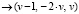
Возвращается общее решение, в котором t, u – базисные неизвестные, v – свободная неизвестная. Частное решение, возвращаемое встроенной функцией lsolve(A,B), соответствует свободной неизвестной 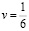
Недостаток применения директивы solve заключается в том, что в рассматриваемом примере базисные неизвестные выбираются единственным образом, хотя в качестве базисных неизвестных можно выбрать любую другую пару неизвестных, т.к. в рассматриваемом примере все миноры второго порядка основной матрицы системы отличны от нуля.
Обойти проблему можно, применяя предлагаемый наиболее близкий к классическому исследованию и решению СЛАУ алгоритм.
Ввести основную матрицу СЛАУ, обозначив ее A, например. В задаче исследовать СЛАУ на совместность задать расширенную матрицу системы А1.
Ввести столбец свободных членов, обозначив его, например, В.
Найти ранг основной матрицы системы: rank(A). Для СЛАУ больших размеров найти rank(A1). Если rank(A)≠rank(A1), СЛАУ несовместна, т.е. решений не имеет, и на этом исследование и решение СЛАУ заканчивается.
Если rank(A) = rank(A1), выбрать отличный от нуля базисный минор F (порядок базисного минора равен рангу основной матрицы СЛАУ) и базисные неизвестные, коэффициенты при которых вошли в базисный минор.
Оставшиеся свободные неизвестные перенести к свободным членам и ввести получившийся столбец С как функцию свободных неизвестных.
Получить общее решение, умножив обратную матрицу 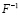
Присвоив свободным неизвестным числовые значения, получить соответствующее частное решение.
Для проверки надо матрицу А умножить на матрицу-столбец В1 решения, составленного из свободных и базисных неизвестных или из значений неизвестных частного решения.
Применение алгоритма рассмотрим на предыдущем примере
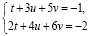
1.
4. Выберем базисными неизвестными 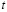
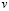
Определитель матрицы F отличен от нуля: 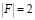
5. Составим матицу С:
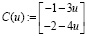
6. Получим общее решение
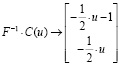
7. Пусть свободная неизвестная
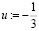
При этом значения базисных неизвестных 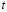
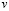
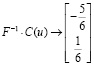
8. Составим столбец
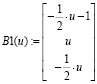
Тогда 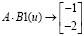
или сделаем проверку для частного решения:
и получим 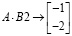
Преимущества предлагаемого алгоритма заключаются в том, что решение СЛАУ осуществляется не формально, когда возвращается единственный вариант ответа. В процессе реализации алгоритма исследуются основные свойства СЛАУ: ранги основной и расширенной матриц системы, выбираются базисные неизвестные и свободные неизвестные, возвращаются общие решения при любом допустимом наборе базисных и свободных неизвестных. Заменяя столбцы основной матрицы СЛАУ столбцом свободных членов со свободными неизвестными, можно получать общее решение и методом Крамера, о чём в учебной литературе упоминаний нет. Вот как это можно осуществить для СЛАУ
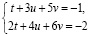
решенной выше матричным методом:
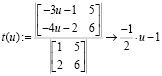
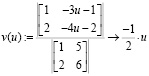
Таким образом, методом Крамера получено общее решение 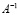
Видео:Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать

Привет студент
ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Приднестровский государственный университет им. Т.Г. Шевченко
Кафедра программного обеспечения вычислительной техники
и автоматизированных систем
КУРСОВАЯ РАБОТА
«Информатика и программирование»
Видео:Решение системы трех уравнений по формулам КрамераСкачать

тема: «ПРОГРАММНАЯ РЕАЛИЗАЦИЯ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ»
студентка группы ИТ13ДР62ИС1
Арабаджи Федор Иванович
ЗАДАНИЕ
на курсовую работу по дисциплине
«ПРОГРАММИРОВАНИЕ»
Студента группы ________ — ___________________
утверждена протоколом кафедры _________ № _____ от «____» ____________ 20___ г.
Цель курсовой работы:
Задачи курсовой работы:
Результаты курсовой работы:
График обязательных консультаций:
Дата сдачи записки на регистрацию «_____» __________20__ г.
Дата защиты курсовой работы «_____» __________20__ г.
Задание принял к исполнению «_____» __________20__ г. ___________/________________/
Руководитель работы ______________________ /________________/
СОДЕРЖАНИЕ
2 ОПИСАНИЕ ПРЕДМЕТНОЙ ОБЛАСТИ………………………………….
2.3 Метод обратной матрицы…………………………………………….
3 РУКОВОДСТВО ПРОГРАММИСТА………………………………………..
3.1 Введение и общие сведения……………………………………………
3.2 Структура программного продукта………………………………….
3.4 Описание исходных текстов программного продукта…………….
3.5 Аппаратная и программная часть…………………………………….
3.6 Результаты тестирования и опытной эксплуатации………………….
4 РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ……………………………………….
4.3 Установка программного продукта……………………………….…..
4.4 Запуск и работа с программным продуктом…………………….……
4.5 Удаление программного продукта…………………………………….
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ…………………………….
Введение
Последние десятилетия характеризуются бурным развитием вычислительной техники. Расширяются области применения вычислительных машин и совершенствуются методы их использования. Созданы универсальные языки программирования и разработаны мощные операционные системы.
Сейчас невозможно представить себе какую-либо область деятельности, обходящуюся без применения компьютерной техники.
Компьютеры используются при проведении различных инженерных расчётов, при решении экономических задач, в процессе управления производством, при получении оценок производственных ситуаций и во многих других случаях.
Решение систем линейных алгебраических уравнений является одной из основных задач линейной алгебры. Эта задача имеет важное прикладное значение при решении научных и технических проблем. Кроме того, является вспомогательной при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований.
Алгебраическое уравнение называется линейным, если оно содержит переменные только в первой степени и не содержит произведений переменных.
Решение систем линейных алгебраических уравнений является одной из фундаментальных задач математики. В частности, она возникает при решении краевых задач для дифференциальных и интегральных уравнений, к которым сводятся реальные проблемы техники, физики, экономики, математики и др. Подобные программы довольно популярны, в особенности среди пользователей глобальной сети Интернет. Они могут быть широко применимы в среде образовательных учреждений. Например, преподавателю необходимо проверить десятки работ студентов в короткий срок или составить варианты контрольных работ, помочь студенту в решении систем линейных уравнений и в их объяснении, так как программа будет содержать краткую теоретическую справку.
Чтобы быстро справится с решением системы линейных уравнений, можно воспользоваться средствами вычислительной техники – написать программу на языке программирования.
Учитывая современные возможности, можно облегчить процесс решения систем линейных уравнений. Данную задачу можно выполнить программно для упрощения и автоматизации процесса решения систем линейных уравнений методом Гаусса, методом Крамера, а также методом обратной матрицы с помощью Windows-приложения, реализованного средствами языка высокого уровня С#.
Данный продукт найдёт своё применение в сфере образования. В частности, например, учащиеся с помощью данной программы смогут проверить правильность решения систем линейных уравнений.
1 постановка задачи
В данной курсовой работе необходимо создать программный продукт при помощи Windows Forms на языке C#, который представлял бы возможность:
- ввода данных с клавиатуры или считывания их из файла с представлением права выбора пользователю;
- решения системы линейных уравнений;
- запись данных в файл;
- доступа к файлу, куда записываются входные и выходные данные.
Программа должна выполнять решение систем линейных уравнений методом Гаусса, методом Крамера или методом обратной матрицы.
Окно программы должно содержать:
- пункты меню: Файл, Правка, Примеры, Справка, О программе;
- поле выбора метода решения системы линейных уравнений;
- поле выбора количества уравнений в системе;
- поля для входных и выходных данных;
- кнопки операций.
Входными данными являются числа вещественного типа, введенные с клавиатуры или считанные из файла. Программа распознает входные данные и производит решение системы одним из выбранных методов.
Результатом работы программы служит отображение получившейся матрицы или определителя (в зависимости от выбранного способа) и корни системы уравнений, полученные в результате решения системы.
2 описание предметной области
Решение систем линейных алгебраических уравнений – одна из фундаментальных задач математики. Система m линейных алгебраических уравнений с n неизвестными (или, линейная система, также употребляется аббревиатура СЛАУ) в линейной алгебре — это система уравнений вида (Рисунок 1)
Рисунок 1- Система уравнений
В системе уравнений (Рисунок 1) m является количеством уравнений, а n – количество неизвестных. x1, x2, … xn – это неизвестные, которые надо определить. a11, a12, … amn – коэффициенты системы, а b1, b2, … bm – свободные члены. Индексы коэффициентов (aij) системы обозначают номера уравнения (i) и неизвестного (j), при котором стоит этот коэффициент, соответственно.
Существуют следующие способы решения систем линейных уравнений:
– метод обратной матрицы.
2.1 Метод Гаусса
Метод Гаусса – классический метод решения системы линейных алгебраических уравнений. Это метод последовательного исключения переменных, когда с помощью элементарных преобразований система уравнений приводится к равносильной системе треугольного вида, из которой последовательно, начиная с последних (по номеру), находятся все переменные системы. Хотя в настоящее время данный метод повсеместно называется методом Гаусса, он был известен и до К.Ф. Гаусса. Первое известное описание данного метода приведено в китайском трактате «Математика в девяти книгах», составленном между первым веком до н. э. и вторым веком н. э.
Далее приведено более подробное описание метода. Пусть исходная система будет вида (Рисунок 2):
Рисунок 2 — Исходная система уравнений
На рисунке 2.1 указана матрица A, вектор x и вектор b. Матрицей А называется основная матрица системы, вектором x – столбец неизвестных, вектором – столбец свободных членов.
Рисунок 2.1 — Матрица A
Согласно свойству элементарных преобразований над строками, основную матрицу этой системы можно привести к треугольному (или ступенчатому) виду (эти же преобразования нужно применять к столбцу свободных членов), что показано на рисунке 2.2
Рисунок 2.2 — Матрица треугольного вида
При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных xj1, … , xjr.
Тогда переменные xj1, … , xjr называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число βi ≠ 0, где i > r, то рассматриваемая система несовместна, то есть у неё нет ни одного решения.
Пусть βi ≠ 0 для любых i > r. Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом x (см. рисунок 2.3):
Рисунок 2.3- Несовместная система
Если свободным переменным системы (рисунок 2.3) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой системы линейных алгебраических уравнений. Так как эта система получена путём элементарных преобразований над исходной системой, то по теореме об эквивалентности при элементарных преобразованиях системы (рисунок 2) и (рисунок 2.3) эквивалентны, то есть множества их решений совпадают.
2.2 Метод Крамера
Метода Крамера – способ решения систем линейных алгебраических уравнений с числом уравнений равным числу неизвестных с ненулевым главным определителем матрицы коэффициентов системы, причём для таких уравнений решение существует и единственно. Назван по имени Габриэля Крамера, предложившего этот метод в 1750 г.
Рисунок 2.4 — Система линейных уравнений
Для системы n линейных уравнений (рисунок 2.4) с n неизвестными с определителем матрицы системы ≠ 0, решение записывается по формуле показанном на рисунке 2.5:
Рисунок 2.5 — Нахождение решения
i-ый столбец матрицы системы заменяется столбцом свободных членов.
2.3 Метод обратной матрицы
Метод обратной матрицы – метод решения системы линейных алгебраических уравнений, использующий понятие обратной матрицы.
Обратная матрица – такая матрица A −1 , при умножении на которую, исходная матрица A даёт в результате единичную матрицу E (формула 2.6).
Обратная матрица находится по формуле 2.7.
В формуле 2.7 det обозначает определитель.
Если необходимо решить систему линейных уравнений Ax = b, где b – ненулевой вектор, в который входят свободные члены, x – искомый вектор. Если обратная матрица A -1 существует, то x = A -1 b. В противном случае либо размерность пространства решений больше нуля, либо их нет вовсе.
3 ПРОграммная реализация решения задачи
3.1 Введение и общие сведения
Одна из основных задач линейной алгебры – решение систем линейных алгебраических уравнений. Эта задача имеет важное прикладное значение при решении научных и технических проблем. Кроме того, является вспомогательной при реализации многих алгоритмов вычислительной математики, математической физики, обработки результатов экспериментальных исследований.
Программа «MATrix» предназначена для решения систем линейных алгебраических уравнений тремя методами:
- методом Гаусса;
- методом Крамера;
- методом обратной матрицы.
Данный программный продукт значительно упрощает получение корней систем линейных уравнений.
3.2 Структура программного продукта
В процессе разработки программного продукта были реализованы следующие формы:
- Formcs – форма приветсвия;
- MATrix.cs – форма, обеспечивающая решение систем линейных алгебраических уравнений методом Гаусса, методом Крамера или методом обратной матрицы по выбору пользователя;
- About.cs – форма, содержащая информацию о программном продукте.
На рисунке 3.1 изображена функциональная схема.
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Дана система уравнений какая программа верно отражает решение данной системы уравнений
3.14159.. e Число e — основание натурального логарифма, примерно равно
2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности
© Контрольная работа РУ — калькуляторы онлайн
Видео:Система с тремя переменнымиСкачать

Где учитесь?
Для правильного составления решения, укажите:
🎦 Видео
Решение систем уравнений методом подстановкиСкачать

Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

решаем систему уравнений методом подстановкиСкачать

Примеры решения системы уравнений с двумя переменными 3 часть.Скачать