Пусть дана система m-линейных уравнений с n-неизвестными 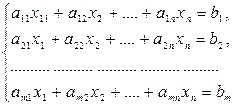
Матрицы
называются соответственно матрицей и расширенной матрицей системы 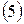
Теорема Кронекера – Капелли: Для совместности системы 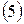

Однородная система уравнений всегда совместна.
Если ранг совместной системы r равен числу неизвестных, т.е. 
Пример 6.Исследовать систему уравнений:
Решение.Рассмотрим расширенную матрицу системы 

Вычтем из третьей строки 1-ую и разделим на 2 ,будем иметь 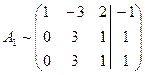
Вычтем, из элементов 3-ей строки соответствующие элементы 2-ой строки 
после этого вычеркнем 3-ю строку, получим 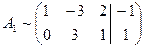
Ранг матрицы 

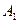
За основные неизвестные примем 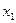
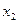
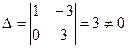

Перепишем систему в виде:
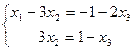
Выразим 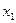
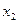

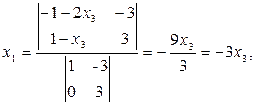
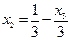
Поэтому общее решение системы: 
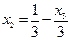
Решение системы линейных уравнений методом Гаусса.
Пусть дана система m-линейных уравнений с n-неизвестными
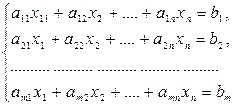
Решение системы линейных уравнений методом Гаусса заключается в последовательном исключении неизвестных и приведении данной системы уравнений к ступенчатому виду с помощью элементарных преобразований.
Практически удобнее приводить к ступенчатому виду не саму систему уравнений, а расширенную матрицу даннойсистемы.
Рассмотрим расширенную матрицу даннойсистемы

Данную матрицу можно привести к ступенчатому виду при помощи следующих элементарных преобразований.
Процесс нахождения коэффициентов ступенчатой системы называется прямым ходом, а процесс нахождения неизвестных обратным ходом.
Пример 7.Решить данную систему методом Гаусса
Решение. Напишем соответствующую расширенную матрицу 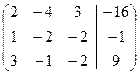
Введем 5-й, так называемый контрольный столбец:
Контрольный столбец, каждый элемент которого равен сумме элементов соответствующей строки, вводим для проверки правильности преобразований. При линейных преобразованиях элементов матрицы такому же преобразованию должны подвергнутся элементы контрольного столбца, при этом каждый элемент контрольного столбца остается равным сумме всех других элементов соответствующей строки преобразованной матрицы. Переход от одной матрицы к другой будем записывать с помощью знака эквивалентности.
Этот процесс называется прямым ходом. Далее используя обратный ход, получим:
Итак получили :
Ответ: 
Контрольные вопросы
2. Обратная матрица
3. Матричный способ решения линейных уравнений.
5.Теорема Кронекера – Капелли
6. Исследование системы линейных уравнений.
7. Решение системы линейных уравнений методом Гаусса.
Задания.
1.Найти ранг матрицы
2. Решить системы матричным способом и методом Гаусса.

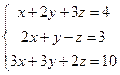


3.Решить матричные уравнения
1) 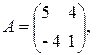

2) 
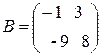
3) 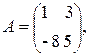
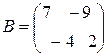
Тема 4.
Векторная алгебра.
1.Векторы. Линейные операции над векторами.
1 0 Вектором называется направленный отрезок 



|
2 0 Векторы параллельные одной прямой, называются коллинеарными
Векторы параллельные одной плоскости, называются компланарными.
Два вектора называются равными, если они коллинеарны, одинаково направлены и имеют одинаковые длины
3 0 Линейные операции.
1) Произведением вектора 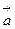
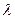

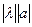
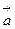
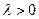
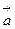

2) Сложение векторов. Суммой векторов 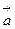
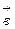
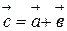
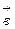

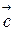
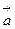
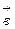
 |
3) Разностью 
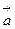
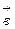
4 0 Свойства линейных операций:
1) 
3) 
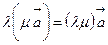

Вектор 

5 0 Проекция вектора на ось. Мы предполагаем, что в пространстве задана некоторая система декартовых прямоугольных координат. Рассмотрим произвольный вектор 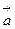
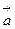
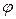
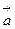

Проекция суммы векторов на ось, равна сумме проекций этих векторов на эту ось:
Пример1. На плоскости даны точки А(0,-2), В(4,2), С(4,-2). В начале координат приложены силы 
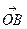

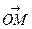

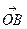
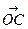
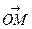
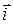
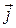
Решение. Имеем 


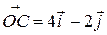



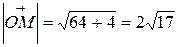
- Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
- Способ №1. Вычисление рангов по определению.
- Способ №2. Вычисление ранга методом элементарных преобразований.
- 92. Однородная система линейных уравнений (ОСЛУ)
- Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли
- 📽️ Видео
Видео:Матричный метод решения систем уравненийСкачать

Теорема Кронекера-Капелли. Исследование систем линейных уравнений на совместность. Первая часть.
Исследовать систему линейных агебраических уравнений (СЛАУ) на совместность означает выяснить, есть у этой системы решения, или же их нет. Ну и если решения есть, то указать сколько их.
Нам понадобятся сведения из темы «Система линейных алгебраических уравнений. Основные термины. Матричная форма записи». В частности, нужны такие понятия, как матрица системы и расширенная матрица системы, поскольку именно на них опирается формулировка теоремы Кронекера-Капелли. Как обычно, матрицу системы будем обозначать буквой $A$, а расширенную матрицу системы – буквой $widetilde$.
Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы, т.е. $rang A=rangwidetilde$.
Следствие из теоремы Кронекера-Капелли
Заметьте, что сформулированная теорема и следствие из неё не указывают, как найти решение СЛАУ. С их помощью можно лишь выяснить, существуют эти решения или нет, а если существуют – то сколько.
Исследовать СЛАУ $ left <begin& -3x_1+9x_2-7x_3=17;\ & -x_1+2x_2-4x_3=9;\ & 4x_1-2x_2+19x_3=-42. endright.$ на совместность. Если СЛАУ совместна, указать количество решений.
Чтобы выяснить наличие решений заданной СЛАУ, используем теорему Кронекера-Капелли. Нам понадобятся матрица системы $A$ и расширенная матрица системы $widetilde$, запишем их:
Видео:Метод Крамера за 3 минуты. Решение системы линейных уравнений - bezbotvyСкачать

Способ №1. Вычисление рангов по определению.
Согласно определению, ранг – это наивысший порядок миноров матрицы, среди которых есть хоть один, отличный от нуля. Обычно исследование начинают с миноров первого порядка, но здесь удобнее приступить сразу к вычислению минора третьего порядка матрицы $A$. Элементы минора третьего порядка находятся на пересечении трёх строк и трёх столбцов рассматриваемой матрицы. Так как матрица $A$ содержит всего 3 строки и 3 столбца, то минор третьего порядка матрицы $A$ – это определитель матрицы $A$, т.е. $Delta A$. Для вычисления определителя применим формулу №2 из темы «Формулы для вычисления определителей второго и третьего порядков»:
$$ Delta A=left| begin -3 & 9 & -7 \ -1 & 2 & -4 \ 4 & -2 & 19 end right|=-21. $$
Итак, есть минор третьего порядка матрицы $A$, который не равен нулю. Минор четвёртого порядка составить невозможно, так как для него требуется 4 строки и 4 столбца, а в матрице $A$ всего 3 строки и 3 столбца. Итак, наивысший порядок миноров матрицы $A$, среди которых есть хотя бы один не равный нулю, равен 3. Следовательно, $rang A=3$.
Задача решена. Какие недостатки и преимущества имеет данный способ? Для начала поговорим о плюсах. Во-первых, нам понадобилось найти всего один определитель. После этого мы сразу сделали вывод о количестве решений. Обычно в стандартных типовых расчётах даются системы уравнений, которые содержат три неизвестных и имеют единственное решение. Для таких систем данный метод очень даже удобен, ибо мы заранее знаем, что решение есть (иначе примера не было бы в типовом расчёте). Т.е. нам остаётся только показать наличие решения наиболее быстрым способом. Во-вторых, вычисленное значение определителя матрицы системы (т.е. $Delta A$) пригодится после: когда станем решать заданную систему методом Крамера или с помощью обратной матрицы.
Однако метод вычисления ранга по определению нежелательно применять, если матрица системы $A$ является прямоугольной. В этом случае лучше применить второй метод, о котором пойдёт речь ниже. Кроме того, если $Delta A=0$, то мы ничего не сможем сказать о количестве решений заданной неоднородной СЛАУ. Может, СЛАУ имеет бесконечное количество решений, а может – ни одного. Если $Delta A=0$, то требуется дополнительное исследование, которое зачастую является громоздким.
Подводя итог сказанному, отмечу, что первый способ хорош для тех СЛАУ, у которых матрица системы квадратна. При этом сама СЛАУ содержит три или четыре неизвестных и взята из стандартных типовых расчетов или контрольных работ.
Видео:Математика без Ху!ни. Метод Гаусса. Совместность системы. Ранг матрицы.Скачать

Способ №2. Вычисление ранга методом элементарных преобразований.
Какие преимущества второго способа? Главное преимущество – это его универсальность. Нам совершенно неважно, является ли матрица системы квадратной или нет. Кроме того, мы фактически провели преобразования прямого хода метода Гаусса. Осталось лишь пару действий, и мы смогли бы получить решение данной СЛАУ. Честно говоря, второй способ нравится мне более первого, но выбор – это дело вкуса.
Ответ: Заданная СЛАУ совместна и определена.
$$ left( begin 1 & -1 & 2 & -1\ -1 & 2 & -3 & 3 \ 2 & -3 & 5 & -4 \ 3 & -2 & 5 & 1 \ 2 & -1 & 3 & 2 end right) begin phantom\r_2+r_1\r_3-2r_1\ r_4-3r_1\r_5-2r_1endrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & -1 & 1 & -2 \ 0 & 1 & -1 & 4 \ 0 & 1 & -1 & 4 end right) begin phantom\phantom\r_3-r_2\ r_4-r_2\r_5+r_2endrightarrow\ $$ $$ rightarrowleft( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 end right) begin phantom\phantom\phantom\ r_4-r_3\phantomendrightarrow left( begin 1 & -1 & 2 & -1\ 0 & 1 & -1 & 2 \ 0 & 0 & 0 & 2 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 end right) $$
Расширенная матрица системы приведена к ступенчатому виду. Ранг ступенчатой матрицы равен количеству её ненулевых строк, поэтому $rangwidetilde=3$. Матрица $A$ (до черты) тоже приведена к ступенчатому виду, и ранг её равен 2, $rang=2$.
Ответ: система несовместна.
Приводим расширенную матрицу системы к ступенчатому виду:
$$ left( begin 2 & 0 & 7 & -5 & 11 & 42\ 1 & -2 & 3 & 0 & 2 & 17 \ -3 & 9 & -11 & 0 & -7 & -64 \ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) overset<r_1leftrightarrow> $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 2 & 0 & 7 & -5 & 11 & 42\ -3 & 9 & -11 & 0 & -7 & -64\ -5 & 17 & -16 & -5 & -4 & -90 \ 7 & -17 & 23 & 0 & 15 & 132 end right) begin phantom\ r_2-2r_1 \r_3+3r_1 \ r_4+5r_1 \ r_5-7r_1 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 3 & -2 & 0 & -1 & -13\ 0 & 7 & -1 & -5 & 6 & -5 \ 0 & -3 & 2 & 0 & 1 & 13 end right) begin phantom\ phantom\4r_3+3r_2 \ 4r_4-7r_2 \ 4r_5+3r_2 end rightarrow $$ $$ rightarrowleft( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & -11 & 15 & -25 & -76 \ 0 & 0 & 11 & -15 & 25 & 76 end right) begin phantom\ phantom\phantom \ r_4-r_3 \ r_5+r_2 end rightarrow left( begin 1 & -2 & 3 & 0 & 2 & 17\ 0 & 4 & 1 & -5 & 7 & 8\ 0 & 0 & -11 & 15 & -25 & -76\ 0 & 0 & 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 & 0 & 0 end right) $$
Мы привели расширенную матрицу системы и саму матрицу системы к ступенчатому виду. Ранг расширенной матрицы системы равен трём, ранг матрицы системы также равен трём. Так как система содержит $n=5$ неизвестных, т.е. $rangwidetilde=ranglt$, то согласно пункту №2 следствия из теоремы Кронекера-Капелли данная система является неопределённой, т.е. имеет бесконечное количество решений.
Ответ: система является неопределённой.
Во второй части мы разберём примеры, которые нередко включают в типовые расчёты или контрольные работы по высшей математике: исследование на совместность и решение СЛАУ в зависимости от значений параметров, входящих в неё.
Видео:Лекция 13. Исследование систем линейных уравнений. Теорема Кронекера — Капелли.Скачать

92. Однородная система линейных уравнений (ОСЛУ)
Пусть дана однородная система M Линейных уравнений с N неизвестными:

Каждое решение системы (2) вектор в арифметическом N-мерном пространстве Рn. Очевидно, что нулевой вектор 0 = (0, 0, . 0) является решением системы (1). Обозначим через Х0 множество решений системы (1). Тогда имеет место следующая теорема о структуре множества решений однородной системы линейных уравнений.
Определение 1. Подмножество L ≠ Æ векторного пространства V называется подпространством V, если
.Теорема 2. Множество Х0 Всех решений ОСЛУ (2) образует подпространство размерности n — r арифметического n-мерного пространстве Рn, Где N — число неизвестных в системе, r — ранг матрицы системы.
Доказательство. В силу сказанного выше Х0 Í Рn , Х0 ≠ Æ . Пусть вектора A = (A1,A2, . AN), B = (B1,B2, . BN) € Х0. Тогда по определению выполняются следующие системы верные равенства:
К каждому равенству системы (7) прибавим почленно соответствующее равенство системы (8) и получим систему верных числовых равенств:
Умножая обе части равенств (8) на произвольное число g € Р получаем систему верных числовых равенств:
Отсюда следует, что для любого вектора A € Х0 и любого числа G € Р вектор GA € Х0 . Таким образом по определению Х0 подпространство векторного пространства Рn .
Пусть R =rangA . Докажем, что dimХ0 = N — r. Для этого решая систему (6) методом Гаусса приведем ее с помощью элементарных преобразований и преобразований вычеркивания нулевых уравнений к ступенчатому виду. При этом матрица системы с помощью элементарных преобразований строк и преобразований вычеркивания нулевых строк перейдет к матрице ступенчатого вида, которая будет содержать R строк. При этом в полученной системе ступенчатого вида будет R уравнений. Будем предполагать, что главными неизвестными в полученной системе ступенчатого вида будут первые R неизвестных X1, X2, . xr и полученная система имеет вид:

Где все коэффициенты С11 , С22 , . сrr не равны нулю, неизвестные X1, X2, . Xr — главные, а неизвестные Xr+1, . Xn — свободные. Пусть Xr+1 = AR+1 , . Xn = AN , где AI € P , I = R+1, . N. Из уравнений системы (9) выразим значения главных неизвестных через свободные и получим:
Где Dij € P; I = 1, 2, . R; J = R + 1, . N. Запишем общее решение системы (6) в виде вектор-столбца:
XT =
Таким образом каждое решение системы (6) линейная комбинация N-r решений:
Рассмотрим матрицу, составленную из координат этих векторов,

Так как ранг этой матрицы равен N-r , то строки ее линейно независимы и система векторов (10) линейно независима и по определению базиса она образует базис подпространства Х0 решений однородной системы (6). Следовательно, dim Х0 = N-r . Теорема доказана.
Определение 1. Фундаментальной системой решений однородной системы называется базис подпространства решений системы.
Следствие 1. Любая однородная система линейных уравнений обладает фундаментальной системой решений, состоящей из n-r решений.
Если X1, X1, . XN-r — фундаментальная система решений однородной системы (6), то она обладает свойствами:
1) она линейно независима,
Далее множество решений Х0 однородной системы есть линейная оболочка натянутая на фундаментальную систему решений:
Фундаментальную систему решений однородной системы можно найти по методу, изложенному в доказательстве теоремы 2.
Пример 1. Найти фундаментальную систему решений системы
Приведем систему элементарными преобразованиями к ступенчатому виду:
ХТ = 
И фундаментальная система решений: Х1 = (-1, -2, 1, 0), Х2 = (-2, -3, 0, 1).
По доказанной теореме однородная система имеет только нулевое решение тогда и только тогда, когда размерность подпространства ее решений равна 0, т. е. при N-r = 0, N =r , определитель системы не равен нулю. Тогда получаем следствия.
Следствие 2. Однородная система n линейных уравнений c n неизвестными имеет только одно нулевое решение тогда и только тогда когда определитель системы не равен нулю.
Следствие 3. Однородная система n линейных уравнений c n неизвестными имеет ненулевое решение тогда и только тогда когда определитель системы равен нулю.
Видео:Ранг матрицыСкачать

Условие совместности системы линейных уравнений. Теорема Кронекера-Капелли
Установить, совместна ли система линейных уравнений, с помощью теоремы Кронекера-Капелли часто можно быстрее, чем с помощью метода Гаусса, когда требуется последовательно исключать неизвестные. Основана эта теорема на использовании ранга матрицы.
Теорема Кронекера-Капелли о совместности системы. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг матрицы этой системы равен рангу её расширенной матрицы, то есть чтобы 
Здесь матрица A (матрица системы) — это матрица, составленная из коэффициентов при неизвестных:
В свою очередь матрица В (расширенная матрица) — это матрица, полученная присоединением к матрице системы столбца из свободных членов:
Ранги этих матриц связаны неравенством 
Следствие из теоремы Кронекера-Капелли о числе решений. Пусть для системы m линейных уравнений с n неизвестными выполнено условие совместности, то есть ранг матрицы из коэффициентов системы равен рангу её расширенной матрицы. Тогда верно следующее.
- Если ранг матрицы равен числу неизвестных (
), то система имеет единственное решение.
- Если ранг матрицы системы меньше числа неизвестных (
), то система имеет бесконечно много решений, а именно: некоторым n — r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.
Если ранг матрицы системы линейных уравнений равен числу уравнений, то есть 
В ходе доказательства теоремы Кронекера-Капелли были получены явные формулы для решений системы (в случае её совместности). Если уже известно, что система совместна, то, чтобы найти её решения, необходимо:
1) отыскать в матрице системы A ранга 

2) отбросить те уравнения, которые соответствуют строкам матрицы A, не входящим в минор 
3) члены с коэффициентами, не входящими в 

Пример 1. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений
Если система совместна, то решить её.
Решение. Вычисляем ранг матрицы этой системы и ранг расширенной матрицы. В обоих случаях он равен 3. Следовательно, система линейных уравнений совместна. Так как ранг матрицы системы меньше числа неизвестных, то система имеет бесконечно много решений: одно неизвестное может быть взято произвольно. Минор
отличен от нуля, поэтому последнее уравнение отбрасываем и неизвестному 

Оставшиеся неизвестные определяются из системы
Решая последнюю систему по формулам Крамера или иным способом, находим



Присоединяя сюда 
Пример 2. Следуя теореме Кронекера-Капелли, установить, совместна ли система уравнений
Если система совместна, то решить её.
Решение. Вычисляем ранг матрицы этой системы:

Следовательно, ранг системы равен 3. Определим ранг расширенной матрицы:

Это означает, что ранг расширенной матрицы также равен 3. Следовательно, система совместна, а так как число неизвестных равно рангу матрицы системы, то она имеет единственное решение. Для решения можем использовать первые три уравнения:
Решая последнюю систему по формулам Крамера, находим



📽️ Видео
15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Как найти ранг матрицы (пример) - bezbotvyСкачать

11. Ранг матрицыСкачать

Ранг матрицыСкачать

Решение матричных уравненийСкачать

Решение системы уравнений методом ГауссаСкачать

Найти ранг матрицы при всех значениях параметраСкачать

Как найти ранг матрицы Три способа Разбор на конкретных примерахСкачать

Исследование систем линейных уравнений на совместностьСкачать

Урок 1. Матрицы, определитель матрицы и ранг матрицы | Высшая математика | TutorOnlineСкачать

Линейная алгебра, 6 урок, Ранг матрицыСкачать

Система линейных уравнений. Метод обратной матрицы. Матричный метод.Скачать

12. Метод Гаусса решения систем линейных уравнений. Часть 1.Скачать

Система линейных уравнений. Общее решение. Метод ГауссаСкачать



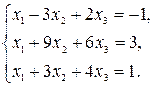


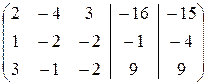
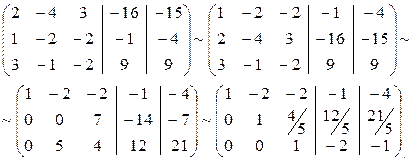

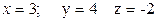





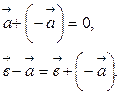


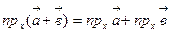







 ), то система имеет единственное решение.
), то система имеет единственное решение. ), то система имеет бесконечно много решений, а именно: некоторым n — r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.
), то система имеет бесконечно много решений, а именно: некоторым n — r неизвестным можно придавать произвольные значения, тогда оставшиеся r неизвестных определятся уже единственным образом.



