Решение систем линейных алгебраических уравнений (СЛАУ), несомненно, является важнейшей темой курса линейной алгебры. Огромное количество задач из всех разделов математики сводится к решению систем линейных уравнений. Этими факторами объясняется причина создания данной статьи. Материал статьи подобран и структурирован так, что с его помощью Вы сможете
- подобрать оптимальный метод решения Вашей системы линейных алгебраических уравнений,
- изучить теорию выбранного метода,
- решить Вашу систему линейных уравнений, рассмотрев подробно разобранные решения характерных примеров и задач.
Краткое описание материала статьи.
Сначала дадим все необходимые определения, понятия и введем обозначения.
Далее рассмотрим методы решения систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных переменных и которые имеют единственное решение. Во-первых, остановимся на методе Крамера, во-вторых, покажем матричный метод решения таких систем уравнений, в-третьих, разберем метод Гаусса (метод последовательного исключения неизвестных переменных). Для закрепления теории обязательно решим несколько СЛАУ различными способами.
После этого перейдем к решению систем линейных алгебраических уравнений общего вида, в которых число уравнений не совпадает с числом неизвестных переменных или основная матрица системы является вырожденной. Сформулируем теорему Кронекера — Капелли, которая позволяет установить совместность СЛАУ. Разберем решение систем (в случае их совместности) с помощью понятия базисного минора матрицы. Также рассмотрим метод Гаусса и подробно опишем решения примеров.
Обязательно остановимся на структуре общего решения однородных и неоднородных систем линейных алгебраических уравнений. Дадим понятие фундаментальной системы решений и покажем, как записывается общее решение СЛАУ с помощью векторов фундаментальной системы решений. Для лучшего понимания разберем несколько примеров.
В заключении рассмотрим системы уравнений, сводящиеся к линейным, а также различные задачи, при решении которых возникают СЛАУ.
Навигация по странице.
- Определения, понятия, обозначения.
- Решение элементарных систем линейных алгебраических уравнений.
- Решение систем линейных уравнений методом Крамера.
- Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
- Решение систем линейных уравнений методом Гаусса.
- Решение систем линейных алгебраических уравнений общего вида.
- Теорема Кронекера – Капелли.
- Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.
- Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.
- Решение систем уравнений, сводящихся к СЛАУ.
- Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Метод Крамера
- Матричный способ решения СЛАУ
- Метод Гаусса
- Ранг матрицы. Теорема Кронекера-Капелли
- Следствия из теоремы Кронекера — Капелли
- Как решать систему уравнений
- Основные понятия
- Линейное уравнение с двумя переменными
- Система двух линейных уравнений с двумя переменными
- Метод подстановки
- Пример 1
- Пример 2
- Пример 3
- Метод сложения
- Система линейных уравнений с тремя переменными
- Решение задач
- Задание 1. Как привести уравнение к стандартному виду ах + by + c = 0?
- Задание 2. Как решать систему уравнений способом подстановки
- Задание 3. Как решать систему уравнений методом сложения
- Задание 4. Решить систему уравнений
- Задание 5. Как решить систему уравнений с двумя неизвестными
- 📽️ Видео
Видео:Неоднородная система линейных уравненийСкачать

Определения, понятия, обозначения.
Будем рассматривать системы из p линейных алгебраических уравнений с n неизвестными переменными ( p может быть равно n ) вида



Такую форму записи СЛАУ называют координатной.
В матричной форме записи эта система уравнений имеет вид 
где 


Если к матрице А добавить в качестве (n+1)-ого столбца матрицу-столбец свободных членов, то получим так называемую расширенную матрицу системы линейных уравнений. Обычно расширенную матрицу обозначают буквой Т , а столбец свободных членов отделяют вертикальной линией от остальных столбцов, то есть,
Решением системы линейных алгебраических уравнений называют набор значений неизвестных переменных 


Если система уравнений имеет хотя бы одно решение, то она называется совместной.
Если система уравнений решений не имеет, то она называется несовместной.
Если СЛАУ имеет единственное решение, то ее называют определенной; если решений больше одного, то – неопределенной.
Если свободные члены всех уравнений системы равны нулю 
Видео:ФСР. Система однородных уравнений. Общее решениеСкачать

Решение элементарных систем линейных алгебраических уравнений.
Если число уравнений системы равно числу неизвестных переменных и определитель ее основной матрицы не равен нулю, то такие СЛАУ будем называть элементарными. Такие системы уравнений имеют единственное решение, причем в случае однородной системы все неизвестные переменные равны нулю.
Такие СЛАУ мы начинали изучать в средней школе. При их решении мы брали какое-нибудь одно уравнение, выражали одну неизвестную переменную через другие и подставляли ее в оставшиеся уравнения, следом брали следующее уравнение, выражали следующую неизвестную переменную и подставляли в другие уравнения и так далее. Или пользовались методом сложения, то есть, складывали два или более уравнений, чтобы исключить некоторые неизвестные переменные. Не будем подробно останавливаться на этих методах, так как они по сути являются модификациями метода Гаусса.
Основными методами решения элементарных систем линейных уравнений являются метод Крамера, матричный метод и метод Гаусса. Разберем их.
Решение систем линейных уравнений методом Крамера.
Пусть нам требуется решить систему линейных алгебраических уравнений

в которой число уравнений равно числу неизвестных переменных и определитель основной матрицы системы отличен от нуля, то есть, 
Пусть 

При таких обозначениях неизвестные переменные вычисляются по формулам метода Крамера как 
Решите систему линейных уравнений методом Крамера 
Основная матрица системы имеет вид 
Так как определитель основной матрицы системы отличен от нуля, то система имеет единственное решение, которое может быть найдено методом Крамера.
Составим и вычислим необходимые определители 




Находим неизвестные переменные по формулам 
Основным недостатком метода Крамера (если это можно назвать недостатком) является трудоемкость вычисления определителей, когда число уравнений системы больше трех.
Для более детальной информации смотрите раздел метод Крамера: вывод формул, примеры, решения.
Решение систем линейных алгебраических уравнений матричным методом (с помощью обратной матрицы).
Пусть система линейных алгебраических уравнений задана в матричной форме 
Так как 




Решите систему линейных уравнений 
Перепишем систему уравнений в матричной форме:
Так как

то СЛАУ можно решать матричным методом. С помощью обратной матрицы решение этой системы может быть найдено как 
Построим обратную матрицу 
Осталось вычислить 



Основная проблема при нахождении решения систем линейных алгебраических уравнений матричным методом заключается в трудоемкости нахождения обратной матрицы, особенно для квадратных матриц порядка выше третьего.
Более подробное описание теории и дополнительные примеры смотрите в статье матричный метод решения систем линейных уравнений.
Решение систем линейных уравнений методом Гаусса.
Пусть нам требуется найти решение системы из n линейных уравнений с n неизвестными переменными 
определитель основной матрицы которой отличен от нуля.
Суть метода Гаусса состоит в последовательном исключении неизвестных переменных: сначала исключается x1 из всех уравнений системы, начиная со второго, далее исключается x2 из всех уравнений, начиная с третьего, и так далее, пока в последнем уравнении останется только неизвестная переменная xn . Такой процесс преобразования уравнений системы для последовательного исключения неизвестных переменных называется прямым ходом метода Гаусса. После завершения прямого хода метода Гаусса из последнего уравнения находится xn , с помощью этого значения из предпоследнего уравнения вычисляется xn-1 , и так далее, из первого уравнения находится x1 . Процесс вычисления неизвестных переменных при движении от последнего уравнения системы к первому называется обратным ходом метода Гаусса.
Кратко опишем алгоритм исключения неизвестных переменных.
Будем считать, что 




где 

К такому же результату мы бы пришли, если бы выразили x1 через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x1 исключена из всех уравнений, начиная со второго.
Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке
Будем считать, что 

Для этого к третьему уравнению системы прибавим второе, умноженное на 



где 

Далее приступаем к исключению неизвестной x3 , при этом действуем аналогично с отмеченной на рисунке частью системы
Так продолжаем прямой ход метода Гаусса пока система не примет вид
С этого момента начинаем обратный ход метода Гаусса: вычисляем xn из последнего уравнения как 
Решите систему линейных уравнений 
Исключим неизвестную переменную x1 из второго и третьего уравнения системы. Для этого к обеим частям второго и третьего уравнений прибавим соответствующие части первого уравнения, умноженные на 

Теперь из третьего уравнения исключим x2 , прибавив к его левой и правой частям левую и правую части второго уравнения, умноженные на 
На этом прямой ход метода Гаусса закончен, начинаем обратный ход.
Из последнего уравнения полученной системы уравнений находим x3 :
Из второго уравнения получаем 
Из первого уравнения находим оставшуюся неизвестную переменную и этим завершаем обратный ход метода Гаусса 
Более детальную информацию и дополнительные примеры смотрите в разделе решение элементарных систем линейных алгебраических уравнений методом Гаусса.
Видео:15. Однородная система линейных уравнений / фундаментальная система решенийСкачать

Решение систем линейных алгебраических уравнений общего вида.
В общем случае число уравнений системы p не совпадает с числом неизвестных переменных n :
Такие СЛАУ могут не иметь решений, иметь единственное решение или иметь бесконечно много решений. Это утверждение относится также к системам уравнений, основная матрица которых квадратная и вырожденная.
Далее нам потребуется понятие минора матрицы и ранга матрицы, которые даны в статье ранг матрицы: определение, методы нахождения, примеры, решения.
Теорема Кронекера – Капелли.
Прежде чем находить решение системы линейных уравнений необходимо установить ее совместность. Ответ на вопрос когда СЛАУ совместна, а когда несовместна, дает теорема Кронекера – Капелли:
для того, чтобы система из p уравнений с n неизвестными ( p может быть равно n ) была совместна необходимо и достаточно, чтобы ранг основной матрицы системы был равен рангу расширенной матрицы, то есть, Rank(A)=Rank(T) .
Рассмотрим на примере применение теоремы Кронекера – Капелли для определения совместности системы линейных уравнений.
Выясните, имеет ли система линейных уравнений 
Найдем ранг основной матрицы системы 

Так как все окаймляющие миноры третьего порядка равны нулю, то ранг основной матрицы равен двум.
В свою очередь ранг расширенной матрицы 

отличен от нуля.
Таким образом, , следовательно, по теореме Кронекера – Капелли можно сделать вывод, что исходная система линейных уравнений несовместна.
система решений не имеет.
Итак, мы научились устанавливать несовместность системы с помощью теоремы Кронекера – Капелли.
А как же находить решение СЛАУ, если установлена ее совместность?
Для этого нам потребуется понятие базисного минора матрицы и теорема о ранге матрицы.
Минор наивысшего порядка матрицы А , отличный от нуля, называется базисным.
Из определения базисного минора следует, что его порядок равен рангу матрицы. Для ненулевой матрицы А базисных миноров может быть несколько, один базисный минор есть всегда.
Для примера рассмотрим матрицу 
Все миноры третьего порядка этой матрицы равны нулю, так как элементы третьей строки этой матрицы представляют собой сумму соответствующих элементов первой и второй строк.
Базисными являются следующие миноры второго порядка, так как они отличны от нуля
Миноры 
Теорема о ранге матрицы.
Если ранг матрицы порядка p на n равен r , то все элементы строк (и столбцов) матрицы, не образующие выбранный базисный минор, линейно выражаются через соответствующие элементы строк (и столбцов), образующих базисный минор.
Что нам дает теорема о ранге матрицы?
Если по теореме Кронекера – Капелли мы установили совместность системы, то выбираем любой базисный минор основной матрицы системы (его порядок равен r ), и исключаем из системы все уравнения, которые не образуют выбранный базисный минор. Полученная таким образом СЛАУ будет эквивалентна исходной, так как отброшенные уравнения все равно излишни (они согласно теореме о ранге матрицы являются линейной комбинацией оставшихся уравнений).
В итоге, после отбрасывания излишних уравнений системы, возможны два случая.
Если число уравнений r в полученной системе будет равно числу неизвестных переменных, то она будет определенной и единственное решение можно будет найти методом Крамера, матричным методом или методом Гаусса.
Решите систему линейных алгебраических уравнений 
Ранг основной матрицы системы 



а рассмотренный выше минор второго порядка отличен от нуля. На основании теоремы Кронекера – Капелли можно утверждать совместность исходной системы линейных уравнений, так как Rank(A)=Rank(T)=2 .
В качестве базисного минора возьмем 
Третье уравнение системы не участвует в образовании базисного минора, поэтому исключим его из системы на основании теоремы о ранге матрицы:
Так мы получили элементарную систему линейных алгебраических уравнений. Решим ее методом Крамера:
Если число уравнений r в полученной СЛАУ меньше числа неизвестных переменных n , то в левых частях уравнений оставляем слагаемые, образующие базисный минор, остальные слагаемые переносим в правые части уравнений системы с противоположным знаком.
Неизвестные переменные (их r штук), оставшиеся в левых частях уравнений, называются основными.
Неизвестные переменные (их штук), которые оказались в правых частях, называются свободными.
Теперь считаем, что свободные неизвестные переменные могут принимать произвольные значения, при этом r основных неизвестных переменных будут выражаться через свободные неизвестные переменные единственным образом. Их выражение можно найти решая полученную СЛАУ методом Крамера, матричным методом или методом Гаусса.
Разберем на примере.
Решите систему линейных алгебраических уравнений 
Найдем ранг основной матрицы системы 
Так мы нашли ненулевой минор второго порядка. Начнем поиск ненулевого окаймляющего минора третьего порядка:
Таким образом, ранг основной матрицы равен трем. Ранг расширенной матрицы также равен трем, то есть, система совместна.
Найденный ненулевой минор третьего порядка возьмем в качестве базисного.
Для наглядности покажем элементы, образующие базисный минор:
Оставляем в левой части уравнений системы слагаемые, участвующие в базисном миноре, остальные переносим с противоположными знаками в правые части:
Придадим свободным неизвестным переменным x2 и x5 произвольные значения, то есть, примем 

Полученную элементарную систему линейных алгебраических уравнений решим методом Крамера:
Следовательно, 
В ответе не забываем указать свободные неизвестные переменные.


Чтобы решить систему линейных алгебраических уравнений общего вида, сначала выясняем ее совместность, используя теорему Кронекера – Капелли. Если ранг основной матрицы не равен рангу расширенной матрицы, то делаем вывод о несовместности системы.
Если ранг основной матрицы равен рангу расширенной матрицы, то выбираем базисный минор и отбрасываем уравнения системы, которые не участвуют в образовании выбранного базисного минора.
Если порядок базисного минора равен числу неизвестных переменных, то СЛАУ имеет единственное решение, которое находим любым известным нам методом.
Если порядок базисного минора меньше числа неизвестных переменных, то в левой части уравнений системы оставляем слагаемые с основными неизвестными переменными, остальные слагаемые переносим в правые части и придаем свободным неизвестным переменным произвольные значения. Из полученной системы линейных уравнений находим основные неизвестные переменные методом Крамера, матричным методом или методом Гаусса.
Метод Гаусса для решения систем линейных алгебраических уравнений общего вида.
Методом Гаусса можно решать системы линейных алгебраических уравнений любого вида без предварительного их исследования на совместность. Процесс последовательного исключения неизвестных переменных позволяет сделать вывод как о совместности, так и о несовместности СЛАУ, а в случае существования решения дает возможность отыскать его.
С точки зрения вычислительной работы метод Гаусса является предпочтительным.
Запись общего решения однородных и неоднородных систем линейных алгебраических с помощью векторов фундаментальной системы решений.
В этом разделе речь пойдет о совместных однородных и неоднородных системах линейных алгебраических уравнений, имеющих бесконечное множество решений.
Разберемся сначала с однородными системами.
Фундаментальной системой решений однородной системы из p линейных алгебраических уравнений с n неизвестными переменными называют совокупность линейно независимых решений этой системы, где r – порядок базисного минора основной матрицы системы.
Если обозначить линейно независимые решения однородной СЛАУ как ( – это матрицы столбцы размерности n на 1 ), то общее решение этой однородной системы 

Что обозначает термин общее решение однородной системы линейных алгебраических уравнений (орослау)?
Смысл прост: формула 

Таким образом, если мы найдем фундаментальную систему решений, то мы сможем задать все решения этой однородной СЛАУ как 
Покажем процесс построения фундаментальной системы решений однородной СЛАУ.
Выбираем базисный минор исходной системы линейных уравнений, исключаем все остальные уравнения из системы и переносим в правые части уравнений системы с противоположными знаками все слагаемые, содержащие свободные неизвестные переменные. Придадим свободным неизвестным переменным значения 1,0,0,…,0 и вычислим основные неизвестные, решив полученную элементарную систему линейных уравнений любым способом, например, методом Крамера. Так будет получено X (1) — первое решение фундаментальной системы. Если придать свободным неизвестным значения 0,1,0,0,…,0 и вычислить при этом основные неизвестные, то получим X (2) . И так далее. Если свободным неизвестным переменным придадим значения 0,0,…,0,1 и вычислим основные неизвестные, то получим X (n-r) . Так будет построена фундаментальная система решений однородной СЛАУ и может быть записано ее общее решение в виде 
Для неоднородных систем линейных алгебраических уравнений общее решение представляется в виде 


Разберем на примерах.
Найдите фундаментальную систему решений и общее решение однородной системы линейных алгебраических уравнений 
Ранг основной матрицы однородных систем линейных уравнений всегда равен рангу расширенной матрицы. Найдем ранг основной матрицы методом окаймляющих миноров. В качестве ненулевого минора первого порядка возьмем элемент основной матрицы системы. Найдем окаймляющий ненулевой минор второго порядка:
Минор второго порядка, отличный от нуля, найден. Переберем окаймляющие его миноры третьего порядка в поисках ненулевого:
Все окаймляющие миноры третьего порядка равны нулю, следовательно, ранг основной и расширенной матрицы равен двум. Базисным минором возьмем 
Третье уравнение исходной СЛАУ не участвует в образовании базисного минора, поэтому, может быть исключено:
Оставляем в правых частях уравнений слагаемые, содержащие основные неизвестные, а в правые части переносим слагаемые со свободными неизвестными:
Построим фундаментальную систему решений исходной однородной системы линейных уравнений. Фундаментальная система решений данной СЛАУ состоит из двух решений, так как исходная СЛАУ содержит четыре неизвестных переменных, а порядок ее базисного минора равен двум. Для нахождения X (1) придадим свободным неизвестным переменным значения , тогда основные неизвестные найдем из системы уравнений 
Решим ее методом Крамера:
Таким образом, 
Теперь построим X (2) . Для этого придадим свободным неизвестным переменным значения , тогда основные неизвестные найдем из системы линейных уравнений 
Опять воспользуемся методом Крамера:
Получаем 
Так мы получили два вектора фундаментальной системы решений 


Найдите общее решение неоднородной системы линейных алгебраических уравнений 
Общее решение этой системы уравнений будем искать в виде 
Исходной неоднородной СЛАУ соответствует однородная система 
общее решение которой мы нашли в предыдущем примере 
Следовательно, нам осталось найти частное решение неоднородной системы линейных алгебраических уравнений 
Ранг основной матрицы системы равен двум, ранг расширенной матрицы системы также равен двум, так как все миноры третьего порядка, окаймляющие минор 

Для нахождения 

Имеем 

где C1 и C2 – произвольные числа.
Следует заметить, что решения неопределенной однородной системы линейных алгебраических уравнений порождают линейное пространство размерности , базисом которого является фундаментальная система решений.
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Решение систем уравнений, сводящихся к СЛАУ.
Некоторые системы уравнений с помощью замены переменных можно свести к линейным. Рассмотрим несколько примеров.
Видео:Задача 17 ЕГЭ профильный. Параметры с нуляСкачать

Методы решения систем линейных алгебраических уравнений (СЛАУ) с примерами
Содержание:
Видео:#17. Плавающий центр окружности — красивая задача с параметром!Скачать

Методы решения систем линейных алгебраических уравнений (СЛАУ)
Метод Крамера
Определение: Системой линейных алгебраических уравнений (СЛАУ) называется выражение
Определение: Определитель, составленный из коэффициентов при неизвестных, называется главным определителем системы
Крамер предложил следующий метод решения СЛАУ: умножим главный определитель на 
Второй столбец умножим на 



Согласно записи СЛАУ первый столбец получившегося определителя представляет собой столбец свободных коэффициентов, т.е.
Определение: Определитель 
Поступая аналогично тому, как описано выше, найдем все вспомогательные определители СЛАУ:
31. Для того чтобы найти вспомогательный определитель i, надо в главном определителе СЛАУ заменить столбец i на столбец свободных коэффициентов.
Определение: Полученные выше соотношения называются формулами Крамера. Используя формулы Крамера, находят неизвестные величины 
- если главный определитель системы отличен от нуля (
), то система имеет единственное решение;
- если главный определитель системы равен нулю (
), а хотя бы один из вспомогательных определителей отличен от нуля (
или
, или, . или
), то система не имеет решений (деление на нуль запрещено);
- если все определители системы равны нулю (
), то система имеет бесчисленное множество решений.
Пример:
Решить СЛАУ методом Крамера
Решение:
Прежде всего, обращаем внимание на то, что в последнем уравнении переменные записаны в неправильном порядке, в этом случае говорят, что СЛАУ записана в ненормализованном виде. Нормализуем СЛАУ, для чего запишем неизвестные в последнем уравнении системы в правильном порядке, чтобы одноименные неизвестные были записаны друг под другом
Найдем главный определитель СЛАУ (раскрываем по первой строке)
Так как главный определитель системы отличен от нуля, то СЛАУ имеет единственное решение. Найдем три вспомогательных определителя
Воспользуемся формулами Крамера
Замечание: После нахождения решения СЛАУ надо обязательно провести проверку, для чего найденные числовые значения неизвестных подставляется в нормализованную систему линейных алгебраических уравнений.
Выполним проверку 
Матричный способ решения СЛАУ
Для решения СЛАУ матричным способом введем в рассмотрение матрицу, составленную из коэффициентов при неизвестных 

Тогда СЛАУ можно записать в матричном виде 





Пример:
Решить СЛАУ матричным способом
Решение:
Введем в рассмотрение следующие матрицы
Найдем матрицу 
Пример:
Решение:
Найдем алгебраические дополнения всех элементов 


Отсюда находим, что х = 1; y = l; z = l.
Метод Гаусса
Метод Гаусса или метод исключения неизвестных состоит в том, чтобы за счет элементарных преобразований привести СЛАУ к треугольному виду. Покажем использование расширенной матрицы, составленной из коэффициентов при неизвестных и расширенной за счет столбца свободных коэффициентов, для приведения СЛАУ к треугольному виду на примере системы, рассматриваемой в этой лекции. Расширенная матрица для СЛАУ имеет вид:
Замечание: В методе Гаусса желательно, чтобы первая строка расширенной матрицы начиналась с единицы.
Обменяем в расширенной матрице первую и вторую строки местами, получим 

Умножим элементы первой строки на (—1) и прибавим к соответствующим элементам третьей строки 

Из первого уравнения находим, что х = 1.
Вывод: Из вышеизложенного материала следует, что вне зависимости от
способа решения СЛАУ всегда должен получаться один и тот же ответ.
Замечание: После нахождения решения СЛАУ надо обязательно выполнить проверку, то есть подставить полученные значения неизвестных в заданную СЛАУ и убедиться в тождественности левой части всех равенств системы соответствующим правым частям. Отметим, что задание СЛАУ всегда верно, то есть, если проверка показывает нарушение оговоренной тождественности, то надо искать ошибку в проведенных вычислениях.
Ранг матрицы. Теорема Кронекера-Капелли
Определение: Рангом матрицы 
Если 
При вычислении ранга необходимо начинать вычислять миноры 2 порядка, затем миноры 3 порядка и так далее, пока не будут найдены миноры, обращающиеся в нуль. Если все миноры порядка p равны нулю, то и все миноры, порядок которых больше p, равны нулю.
Пример:
Найти ранг матрицы
Решение:
Очевидно, что среди миноров второго порядка есть миноры отличные от нуля, например, 


Теорема Кронекера-Капелли (критерий совместности СЛАУ). Для совместности системы линейных алгебраических уравнений (СЛАУ) необходимо и достаточно, чтобы ранг расширенной матрицы совпадал с рангом основной матрицы, составленной из коэффициентов при неизвестных величинах.
Видео:Найдите все значения параметра а, при которых система имеет единственное решениеСкачать

Следствия из теоремы Кронекера — Капелли
Следствие: Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение (то есть она определенная).
Следствие: Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесчисленное множество решений (т.е. она неопределенная).
В случае неопределенной системы решения ищут следующим образом: выбираются главные неизвестные, число которых равно рангу, а остальные неизвестные считаются свободными; далее главные неизвестные выражаются через свободные и получают множество решений, зависящих от свободных неизвестных. Это множество решений называется общим решением системы. Придавая свободным неизвестным различные произвольные значения, получим бесчисленное множество решений, каждое из которых называется частным решением системы.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
- Экстремум функции
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Линейные диофантовы уравненияСкачать

Как решать систему уравнений
О чем эта статья:
8 класс, 9 класс, ЕГЭ/ОГЭ
Видео:Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Основные понятия
Алгебра в 8 и 9 классе становится сложнее. Но если изучать темы последовательно и регулярно практиковаться в тетрадке и онлайн — ходить на уроки математики будет не так страшно.
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Значение неизвестных нужно найти так, чтобы при их подстановке в исходное уравнение получилось верное числовое равенство.
Например, возьмем 3 + 4 = 7. При вычислении левой части получается верное числовое равенство, то есть 7 = 7.
Уравнением можно назвать, например, равенство 3 + x = 7 с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Система уравнений — это несколько уравнений, для которых надо найти значения неизвестных, каждое из которых соответствует данным уравнениям.
Так как существует множество уравнений, составленных с их использованием систем уравнений также много. Поэтому для удобства изучения существуют отдельные группы по схожим характеристикам. Рассмотрим способы решения систем уравнений.
Видео:Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Линейное уравнение с двумя переменными
Уравнение вида ax + by + c = 0 называется линейным уравнением с двумя переменными x и y, где a, b, c — числа.
Решением этого уравнения называют любую пару чисел (x; y), которая соответствует этому уравнению и обращает его в верное числовое равенство.
Теорема, которую нужно запомнить: если в линейном уравнение есть хотя бы один не нулевой коэффициент при переменной — его графиком будет прямая линия.
Вот алгоритм построения графика ax + by + c = 0, где a ≠ 0, b ≠ 0:
Дать переменной 𝑥 конкретное значение x = x₁, и найти значение y = y₁ при ax₁ + by + c = 0.
Дать x другое значение x = x₂, и найти соответствующее значение y = y₂ при ax₂ + by + c = 0.
Построить на координатной плоскости xy точки: (x₁; y₁); (x₂; y₂).
Провести прямую через эти две точки и вуаля — график готов.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Видео:Обратная теорема Виета - ЛЕГКО!Скачать

Система двух линейных уравнений с двумя переменными
Для ax + by + c = 0 можно сколько угодно раз брать произвольные значение для x и находить значения для y. Решений в таком случае может быть бесчисленное множество.
Система линейных уравнений (ЛУ) с двумя переменными образуется в случае, когда x и y связаны не одним, а двумя уравнениями. Такая система может иметь одно решение или не иметь решений совсем. Выглядит это вот так:
Из первого линейного уравнения a₁x + b₁y + c₁ = 0 можно получить линейную функцию, при условии если b₁ ≠ 0: y = k₁x + m₁. График — прямая линия.
Из второго ЛУ a₂x + b₂y + c₂ = 0 можно получить линейную функцию, если b₂ ≠ 0: y = k₂x + m₂. Графиком снова будет прямая линия.
Можно записать систему иначе:
Множеством решений первого ЛУ является множество точек, лежащих на определенной прямой, аналогично и для второго ЛУ. Если эти прямые пересекаются — у системы есть единственное решение. Это возможно при условии, если k₁ ≠ k₂.
Две прямые могут быть параллельны, а значит, они никогда не пересекутся и система не будет иметь решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ ≠ m₂.
Две прямые могут совпасть, и тогда каждая точка будет решением, а у системы будет бесчисленное множество решений. Это возможно при следующих условиях: k₁ = k₂ и m₁ = m₂.
Видео:Решение систем уравнений второй степени. Алгебра, 9 классСкачать

Метод подстановки
Разберем решение систем уравнений методом подстановки. Вот алгоритм при переменных x и y:
Выразить одну переменную через другую из более простого уравнения системы.
Подставить то, что получилось на место этой переменной в другое уравнение системы.
Решить полученное уравнение, найти одну из переменных.
Подставить поочередно каждый из найденных корней в уравнение, которое получили на первом шаге, и найти второе неизвестное значение.
Записать ответ. Ответ принято записывать в виде пар значений (x; y).
Решим систему уравнений методом подстановки
Потренируемся решать системы линейных уравнений методом подстановки.
Пример 1
Решите систему уравнений:
x − y = 4
x + 2y = 10
Выразим x из первого уравнения:
x − y = 4
x = 4 + y
Подставим получившееся выражение во второе уравнение вместо x:
x + 2y = 10
4 + y + 2y = 10
Решим второе уравнение относительно переменной y:
4 + y + 2y = 10
4 + 3y = 10
3y = 10 − 4
3y = 6
y = 6 : 3
y = 2
Полученное значение подставим в первое уравнение вместо y и решим уравнение:
x − y = 4
x − 2 = 4
x = 4 + 2
x = 6
Ответ: (6; 2).
Пример 2
Решите систему линейных уравнений:
x + 5y = 7
3x = 4 + 2y
Сначала выразим переменную x из первого уравнения:
x + 5y = 7
x = 7 − 5y
Выражение 7 − 5y подставим вместо переменной x во второе уравнение:
3x = 4 + 2y
3 (7 − 5y) = 4 + 2y
Решим второе линейное уравнение в системе:
3 (7 − 5y) = 4 + 2y
21 − 15y = 4 + 2y
21 − 15y − 2y = 4
21 − 17y = 4
17y = 21 − 4
17y = 17
y = 17 : 17
y = 1
Подставим значение y в первое уравнение и найдем значение x:
x + 5y = 7
x + 5 = 7
x = 7 − 5
x = 2
Ответ: (2; 1).
Пример 3
Решите систему линейных уравнений:
x − 2y = 3
5x + y = 4
Из первого уравнения выразим x:
x − 2y = 3
x = 3 + 2y
Подставим 3 + 2y во второе уравнение системы и решим его:
5x + y = 4
5 (3 + 2y) + y = 4
15 + 10y + y = 4
15 + 11y = 4
11y = 4 − 15
11y = −11
y = −11 : 11
y = −1
Подставим получившееся значение в первое уравнение и решим его:
x − 2y = 3
x − 2 (−1) = 3
x + 2 = 3
x = 3 − 2
x = 1
Ответ: (1; −1).
Видео:Система не имеет решений | система координат с параметром | Параметр 5 | mathus.ruСкачать

Метод сложения
Теперь решим систему уравнений способом сложения. Алгоритм с переменными x и y:
При необходимости умножаем почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами.
Складываем почленно левые и правые части уравнений системы.
Решаем получившееся уравнение с одной переменной.
Находим соответствующие значения второй переменной.
Запишем ответ в в виде пар значений (x; y).
Пример.
Домножим первое уравнение системы на -2, второе оставим без изменений. Система примет вид:
Сложим уравнения, получим
Отсюда y = -3, а, значит, x = 2
Ответ: (2; -3).
Видео:Модальные регуляторы и наблюдатели | Утро с теорией управления, лекция 8Скачать

Система линейных уравнений с тремя переменными
Системы ЛУ с тремя переменными решают так же, как и с двумя. В них присутствуют три неизвестных с коэффициентами и свободный член. Выглядит так:
Решений в таком случае может быть бесчисленное множество. Придавая двум переменным различные значения, можно найти третье значение. Ответ принято записывать в виде тройки значений (x; y; z).
Если x, y, z связаны между собой тремя уравнениями, то образуется система трех ЛУ с тремя переменными. Для решения такой системы можно применять метод подстановки и метод сложения.
Видео:Линейная алгебра: матрицы, определители, метод Крамера. Высшая математикаСкачать

Решение задач
Разберем примеры решения систем уравнений.
Задание 1. Как привести уравнение к стандартному виду ах + by + c = 0?
5x − 8y = 4x − 9y + 3
5x − 8y = 4x − 9y + 3
5x − 8y − 4x + 9y = 3
Задание 2. Как решать систему уравнений способом подстановки
Выразить у из первого уравнения:
Подставить полученное выражение во второе уравнение:
Найти соответствующие значения у:
Задание 3. Как решать систему уравнений методом сложения
- Решение систем линейных уравнений начинается с внимательного просмотра задачи. Заметим, что можно исключить у. Для этого умножим первое уравнение на минус два и сложим со вторым:
- Решаем полученное квадратное уравнение любым способом. Находим его корни:
- Найти у, подставив найденное значение в любое уравнение:
- Ответ: (1; 1), (1; -1).
Задание 4. Решить систему уравнений
Решим второе уравнение и найдем х = 2, х = 5. Подставим значение переменной х в первое уравнение и найдем соответствующее значение у.
Задание 5. Как решить систему уравнений с двумя неизвестными
При у = -2 первое уравнение не имеет решений, при у = 2 получается:
📽️ Видео
Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

ТЕОРЕМА ВИЕТА ЗА 2 МИНУТЫСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Область допустимых значений. ОДЗ в выражении.Скачать

МИНИ-КУРС (2 часть) Параметры 17 задание Профиль от АбеляСкачать









































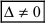 ), то система имеет единственное решение;
), то система имеет единственное решение;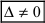 ), а хотя бы один из вспомогательных определителей отличен от нуля (
), а хотя бы один из вспомогательных определителей отличен от нуля ( 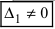 или
или 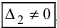 , или, . или
, или, . или 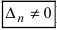 ), то система не имеет решений (деление на нуль запрещено);
), то система не имеет решений (деление на нуль запрещено);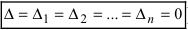 ), то система имеет бесчисленное множество решений.
), то система имеет бесчисленное множество решений.













