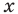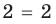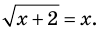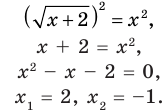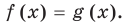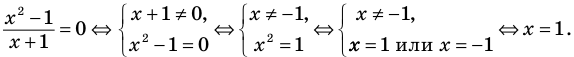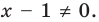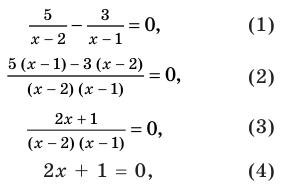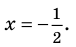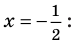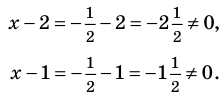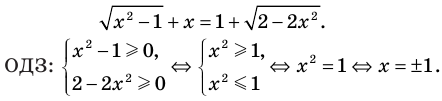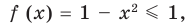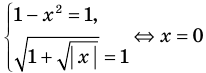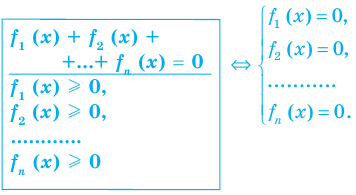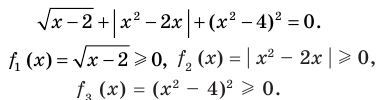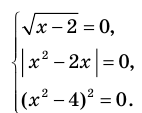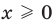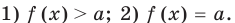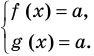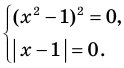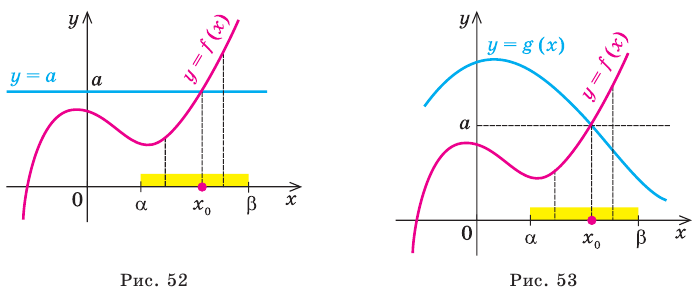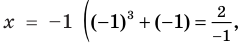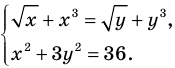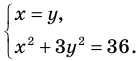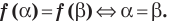О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
- Понятие области определения функции
- Материал со звездочкой
- Области определения основных элементарных функций
- Область определения постоянной функции
- Область определения функции с корнем
- Пример
- Область определения степенной функции
- Область определения показательной функции
- Область определения логарифмической функции
- Пример
- Область определения тригонометрических функций
- Пример
- Область определения обратных тригонометрических функций
- Таблица областей определения функций
- Уравнение — определение и вычисление с примерами решения
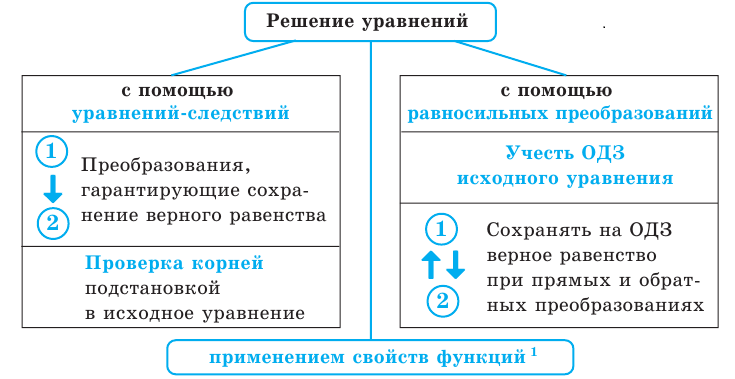
- Уравнения
- Уравнения-следствия и равносильные преобразования уравнений
- Понятие уравнения и его корней
- Область допустимых значений (ОДЗ) уравнения
- Методы решения уравнений
- Уравнения-следствия
- Равносильные уравнения
- Причины появления посторонних корней и потери корней при решении уравнений
- Применение свойств функций к решению уравнений
- Конечная ОДЗ
- Оценка левой и правой частей уравнения
- Использование возрастания и убывания функций к решению уравнений
- Как найти область определения функции?
- Что значит найти область определения
- Ограничение области определения
- Правила нахождения области определения
- Область определения суммы, разности и произведения функций
- Область определения сложной функции
- Область определения дроби
- Область определения логарифма с переменной в основании
- Область определения показательно-степенной функции
- В общем случае
- Таблицы основных результатов
Видео:Область определения функцийСкачать

Понятие области определения функции
Впервые школьники знакомятся с термином «функция» на алгебре в 7 классе, и с каждой четвертью, с каждой новой темой это понятие раскрывается с новых сторон. И, конечно же, усложняются задачки. Сейчас дадим определения ключевым словам и будем находить область определения функции заданной формулой и по графику.
Если каждому значению x из некоторого множества соответствует число y, значит, на этом множестве задана функция. При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Зависимость переменной у от переменной х называют функциональной зависимостью. Записывают так: y = f(x).
Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества.
Из понятия функции сформулируем определение области определения функции.
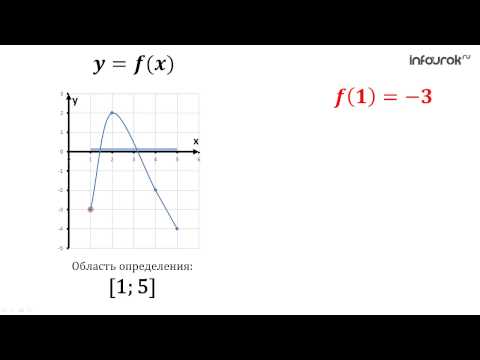
Область определения функции — это множество всех значений аргумента (переменной x). Геометрически — это проекция графика функции на ось Ох. Чтобы обозначить область определения некоторой функции y, используют запись D(y).
Множество значений функции — множество всех значений, которые функция принимает на области определения. Геометрически — это проекция графика функции на ось Оy.
- Например, область значений функции y = x2 — это все числа больше либо равные нулю. Это можно записать так: Е (у): у ≥ 0.
Материал со звездочкой
Старшеклассникам нужно помнить, что у некоторых функций есть собственные обозначения. Например, у тригонометрических. Поэтому в учебниках можно встретить такие записи: D(sin) — область определения функции синус, D(arcsin) — область определения функции арксинус.
Можно также записать D(f), где f — функция синуса или арксинуса. Если функция f определена на множестве значений x, то можно использовать формулировку D(f) = X. Так, например, для того же арксинуса запись будет выглядеть так: D (arcsin) = [-1, 1].
Область определения можно описывать словами, но часто ответ получается громоздким. Поэтому используют специальные обозначения.
Если мы хотим указать на множество чисел, которые лежат в некотором промежутке, то делаем так:
- Через точку с запятой указываем два числа: левую и правую границы промежутка.
- Если граница входит в промежуток, ставим возле нее квадратную скобку, если не входит — круглую.
- Если у промежутка нет правой границы, записываем так: ∞ или +∞. Если нет левой границы, пишем -∞.
- Если нужно описать множество, состоящее из нескольких промежутков, ставим между ними знак объединения: ∪.
Например, все действительные числа от 2 до 5 включительно можно записать так:
Все положительные числа можно описать так:
Ноль не положительное число, поэтому скобка возле него круглая.
Видео:Функция. Область определения функции. Практическая часть. 10 класс.Скачать

Области определения основных элементарных функций
Область определения функции — неотъемлемая часть самой функции. Когда мы вводим какую-либо функцию, то сразу указываем ее область определения.
На уроках алгебры мы последовательно знакомимся с каждой функцией: прямая пропорциональность, линейная функция, функция y = x2 и другие. А области их определения изучаем, как свойства.
Рассмотрим области определения основных элементарных функций.
Видео:9 класс, 15 урок, Определение числовой функции. Область определения, область значения функцииСкачать

Область определения постоянной функции
Постоянная функция задается формулой y = C, то есть f(x) = C, где C — некоторое действительное число. Ее еще называют константа.
Смысл функции — в том, что каждому значению аргумента соответствует значение функции, которое равно C. Поэтому, область определения этой функции — множество всех действительных чисел R.
- Область определения постоянной функции y = -3 — это множество всех действительных чисел: D(y) = (−∞, +∞) или D(y) = R.
- Областью определения функции y = 3 √9 является множество R.
Еще больше наглядных примеров и практики — на курсах по математике в онлайн-школе Skysmart!
Видео:Алгебра 9 класс. Область определения функцииСкачать

Область определения функции с корнем
Функцию с корнем можно определить так: y = n √x, где n — натуральное число больше единицы.
Рассмотрим две вариации такой функции.
Область определения корня зависит от четности или нечетности показателя:
- Если n — четное число, то есть, n = 2m, где m ∈ N, то ее область определения есть множество всех неотрицательных действительных чисел:
- Если показатель корня нечетное число больше единицы, то есть n = 2m+1, при этом m принадлежит к N, то область определения корня — множество всех действительных чисел:
Значит, область определения каждой из функций y = √x, y = 4 √x, y = 6 √x,… есть числовое множество [0, +∞). А область определения функций y = 3 √x, y = 5 √x, y = 7 √x,… — множество (−∞, +∞).
Видео:Что такое аргумент функции, значение функции, область определения функции, область значений функции?Скачать

Пример
Найти область определения функции:
Подкоренное выражение должно быть неотрицательным, но поскольку оно стоит в знаменателе, то равняться нулю не может. Следовательно, для нахождения области определения необходимо решить неравенство x 2 + 4x + 3 > 0.
Для этого решим квадратное уравнение x 2 + 4x + 3 = 0. Находим дискриминант:
D = 16 — 12 = 4 > 0
Дискриминант положительный. Ищем корни:
Значит парабола f(x) = x 2 + 4x + 3 пересекает ось абсцисс в двух точках. Часть параболы расположена ниже оси (неравенство x 2 + 4x + 3 2 + 4x + 3 > 0).
Поскольку коэффициент a = 1 > 0, то ветви параболы смотрят вверх. Можно сделать вывод, что на интервалах (−∞, -3) ∪ (−1, +∞) выполнено неравенство x 2 + 4x + 3 > 0 (ветви параболы уходят вверх на бесконечность), а вершина параболы расположена на промежутке (-3; -1) ниже оси абсцисс, что соответствует неравенству x 2 + 4x + 3
Видео:Область определения функции - 25 функций в одном видеоСкачать

Область определения степенной функции
Степенная функция выглядит так: y = x a , то есть, f(x) = x a , где x — переменная в основании степени, a — некоторое число в показателе степени.
Область определения степенной функции зависит от значения показателя степени.
Перечислим возможные случаи:
- Если a — положительное целое число, то область определения функции есть множество действительных чисел: (−∞, +∞).
- Для нецелых действительных положительных показателей степени: D(f) = [0, +∞).
- Если a — отрицательное целое число, то область определения функции представляет собой множество (−∞, 0) ∪ (0, +∞).
- Для остальных действительных отрицательных a область определения степенной функции — числовой промежуток (0, +∞).
При a = 0 степенная функция y = x a определена для всех действительных значений x, кроме x = 0. Это связано с тем, что мы не определяли 0 0 . А любое отличное от нуля число в нулевой степени равно единице. То есть, при a = 0 функция приобретает вид y = x 0 = 1 на области определения (−∞, 0) ∪ (0, +∞).
Рассмотрим несколько примеров.
- Область определения функций y = x 5 , y = x 12 — множество R, так как показатели степени целые положительные.
- Степенные функции
определены на интервале [0, +∞), так как их показатели положительные, но не целые.
- Область определения функции y = x −2 , как и функции y = x −5 — это множество (−∞, 0) ∪ (0, +∞), так как показатели степени целые отрицательные.
- Область определения степенных функций y = x -√19 , y = x -3e ,
— открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.
Видео:Функция. Область определения и область значений функцииСкачать
Область определения показательной функции
Показательную функцию можно задать формулой y = a x , где переменная x — показатель степени, а — больше нуля и не равно единице.
Область определения показательной функции — это множество R.
Примеры показательных функций:
- y = e x
- y = (√15) x
- y = 13 x .
Область определения каждой из них (−∞, +∞).
Видео:ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ - Алгебра 7 класс - Теория функцийСкачать

Область определения логарифмической функции
Логарифмическая функция выглядит так: y = logax, где где число a > 0 и a ≠ 1. Она определена на множестве всех положительных действительных чисел.
Область определения логарифмической функции или область определения логарифма — это множество всех положительных действительных чисел. То есть, D (loga) = (0, +∞).
Например:
Рассмотрим примеры логарифмических функций:
- y = log7x
- y = lnx
Область определения этих функций есть множество (0, +∞).
Видео:Найти область определения функции #math #егэ #огэ #школа #мгу #алгебра #неравенстваСкачать

Пример
Укажите, какова область определения функции:
Составим и решим систему:
Ответ: область определения: D(f) = (−3, -2) ∪ (−2, +∞).
Видео:Функция. Область определения и область значения функции. Алгебра, 9 классСкачать

Область определения тригонометрических функций
Сначала вспомним, как задавать тригонометрические функции и как увидеть их области определения.
- Функция, которая задается формулой y = sinx, называется синусом, обозначается sin и определяется на множестве всех действительных чисел. Область определения синуса — это множество всех действительных чисел, то есть, D(sin) = R.
- Функция, которая задана формулой y = cosx, называется косинусом, обозначается cos и определяется на множестве R. Область определения функции косинус — множество всех действительных чисел: D(cos) = R.
- Функции, которые заданы формулами y = tgx и y = ctgx, называются тангенсом и котангенсом и обозначаются tg и ctg. Область определения тангенса — это множество всех действительных чисел, кроме чисел
. Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.
Поэтому, если x — аргумент функций тангенс и котангенс, то области определения тангенса и котангенса состоят из всех таких чисел x, что 
Видео:СПОРИМ ты поймешь Математику — Функция и ее свойства, Область определения, Нули ФункцииСкачать

Пример
Найдите область определения функции f(x) = tg2x.
Так как a(x) = 2x, то в область определения не войдут следующие точки:
Перенесем 2 из левой части в знаменатель правой части:
В результате 
Ответ: область определения: 
Видео:Алгебра 9. Урок 10 - Функция. Область определения.Скачать

Область определения обратных тригонометрических функций
Вспомним обратные тригонометрические функции: арксинус, арккосинус, арктангенс и арккотангенс.
- Функция, которая задается формулой y = arcsinx и рассматривается на отрезке [−1, 1], называется арксинусом и обозначается arcsin.
Область определения арксинуса — это множество [−1, 1], то есть, D(arcsin) = [−1, 1].
Функция, которая задается формулой y = arccosx и рассматривается на отрезке [−1, 1], называется арккосинусом и обозначается arccos.
Область определения функции арккосинус — отрезок [−1, 1], то есть, D(arccos) = [−1, 1].
Функции, которые задаются формулами вида y = arctgx и y = arcctgx и рассматриваются на множестве всех действительных чисел, называются арктангенсом и арккотангенсом и обозначаются arctg и arcctg.
Область определения арктангенса и арккотангенса — все множество действительных чисел R. То есть, D(arctg) = R и D(arcctg) = R.
Видео:Найти область определения функции. #ShortsСкачать

Таблица областей определения функций
Области определения основных функций в табличном виде можно распечатать и использовать на уроках, чтобы быстрее решать задачки.
И, помните: чем чаще вы практикуетесь в решении задач — тем быстрее все запомните.
Функция
Область определения функции
Видео:Как найти нули функции? #shortsСкачать

Уравнение — определение и вычисление с примерами решения
Содержание:
Видео:№354 Найти область определения логарифмической функции (АНА 10-11 кл., Алимов Ш.А.)Скачать

Уравнения
Уравнения-следствия и равносильные преобразования уравнений
1. Понятие уравнения и его корней
Определение:
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны
Пример:
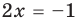
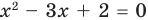
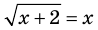
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни или доказать, что их нет
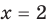
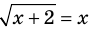
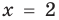
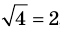
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций 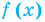
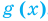
Для уравнения 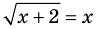
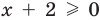
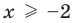
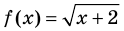

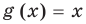
3. Уравнения-следствия
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения.
Пример:
Решение:
► Возведем обе части уравнения в квадрат:
Проверка, 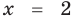
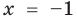
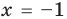
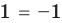
4. Равносильные уравнения
Определение:
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни.
То есть каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого. (Схема решения уравнений с помощью равносильных преобразований приведена в пункте 5 этой таблицы)
Простейшие теоремы
- Если из одной части уравнения перенести в другую слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве)
- Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получим уравнение, равносильное заданному (на ОДЗ заданного уравнения)
5. Схема поиска плана решения уравнений



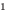
Объяснение и обоснование:
Понятие уравнения и его корней
Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной 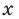
Часто уравнения определяют короче — как равенство с переменной.
Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
Например, уравнение 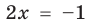
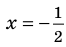
а уравнение 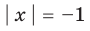
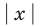
Область допустимых значений (ОДЗ) уравнения
Если задано уравнение 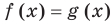
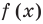
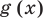
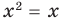
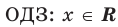
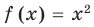
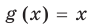
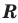
Понятно, что каждый корень данного уравнения принадлежит как области определения функции 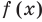
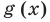
Например, в уравнении 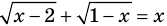
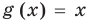
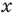
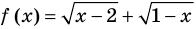
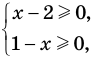
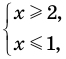
Заметим, что нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.
Методы решения уравнений
Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5-6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств; в курсе алгебры 7-9 классов — равносильные преобразования уравнений, а для приближенного решения уравнений — графический метод.
Графический метод решения уравнений не дает высокой точности нахождения корней уравнения, и с его помощью чаще всего можно получить только грубые приближения корней. Иногда удобно графически определить количество корней уравнения или найти границы, в которых находятся эти корни. В некоторых случаях можно графически доказать, что уравнение не имеет корней. По указанным причинам в школьном курсе алгебры и начал анализа под требованием «решить уравнение» понимается требование «используя методы точного решения, найти корни данного уравнения». Приближенными методами решения уравнений можно пользоваться только тогда, когда об этом говорится в условии задачи (например, если ставится задача решить уравнение графически).
В основном при решении уравнений разных видов нам придется применять один из двух методов решения. Первый из них состоит в том, что данное уравнение заменяется более простым уравнением, имеющим те же корни,— равносильным уравнением. В свою очередь, полученное уравнение заменяется еще более простым, равносильным ему, и т. д. В результате получаем простейшее уравнение, которое равносильно заданному и корни которого легко находятся. Эти корни и только они являются корнями данного уравнения.
Второй метод решения уравнений состоит в том, что данное уравнение заменяется более простым уравнением, среди корней которого находятся все корни данного, то есть так называемым уравнением-следствием. В свою очередь, полученное уравнение заменяется еще более простым уравнением-следствием, и так далее до тех пор, пока не получим простейшее уравнение, корни которого легко находятся. Тогда все корни данного уравнения находятся среди корней последнего уравнения. Поэтому, чтобы найти корни данного уравнения, достаточно корни последнего уравнения подставить в данное и с помощью такой проверки получить корни данного уравнения (и исключить так называемые посторонние корни — те корни последнего уравнения, которые не удовлетворяют заданному).
В следующем пункте будет также показано применение свойств функций к решению уравнений определенного вида.
Уравнения-следствия
Рассмотрим более детально, как можно решать уравнения с помощью уравнений-следствий. При решении уравнений главное — не потерять корни данного уравнения, и поэтому в первую очередь мы должны следить за тем, чтобы каждый корень исходного уравнения оставался корнем следующего. Фактически это и является определением уравнения-следствия:
в том случае, когда каждый корень первого уравнения является корнем второго, второе уравнение называется следствием первого.
Это определение позволяет обосновать такой ориентир: для получения уравнения-следствия достаточно рассмотреть данное уравнение как верное числовое равенство и гарантировать (то есть иметь возможность обосновать), что каждое следующее уравнение мы можем получить как верное числовое равенство.
Действительно, если придерживаться этого ориентира, то каждый корень первого уравнения обращает это уравнение в верное числовое равенство, но тогда и второе уравнение будет верным числовым равенством, то есть рассматриваемое значение переменной является корнем и второго уравнения, а это и означает, что второе уравнение является следствием первого.
Применим приведенный ориентир к уравнению 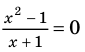
Если правильно то, что дробь равна нулю, то обязательно ее числитель равен нулю. Таким образом, из заданного уравнения получаем уравнение-следствие 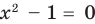
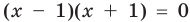
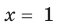
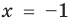
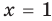
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 9.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один ориентир: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 8. В пункте 3 этой таблицы приведено решение уравнения
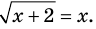
Для решения этого уравнения с помощью уравнений-следствий достаточно данное уравнение рассмотреть как верное числовое равенство и учесть, что в случае когда два числа равны, то и их квадраты также будут равны:
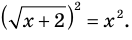
То есть мы гарантируем, что если равенство (1) верно, то и равенство (2) также будет верным, а это и означает (как было показано выше), что уравнение (2) является следствием уравнения (1). Если мы хотя бы один раз использовали уравнения-следствия (а не равносильные преобразования), то можем получить посторонние корни, и тогда в решение обязательно входит проверка полученных корней подстановкой их в заданное уравнение.
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком 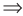
Равносильные уравнения
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 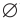
В курсе алгебры и начал анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни, то есть каждый корень первого уравнения является корнем второго и, наоборот, каждый корень второго уравнения является корнем первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения 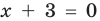
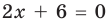
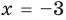
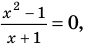
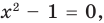
то, как было показано выше, уравнение (3) имеет единственный корень 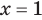
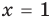
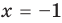
всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень 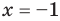
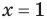
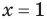
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы).
Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Например, для уравнения 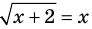
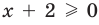

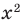
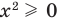
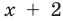


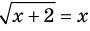
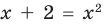
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий. Как указывалось выше, выполняя равносильные преобразования уравнений, необходимо учесть ОДЗ данного уравнения — это и есть первый ориентир для выполнения равносильных преобразований уравнений. По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и, наоборот, каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму.
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при выполнении равносильных преобразований мы должны гарантировать сохранение правильности равенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях — это и является вторым ориентиром для решения уравнений с помощью равносильных преобразований. (Соответствующие ориентиры схематически представлены в пункте 5 табл. 8.)
Например, чтобы решить с помощью равносильных преобразований уравнение 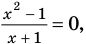
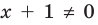
Запись решения в этом случае может быть такой:
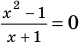
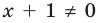
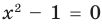
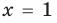
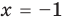
Для выполнения равносильных преобразований уравнений можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности уравнений обобщим также формулировки простейших теорем о равносильности, известных из курса алгебры 7 класса.
Теорема 1. Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований данного уравнения.
Замечание. Для обозначения перехода от данного уравнения к равносильному ему уравнению можно применять специальный значок 
Пример №423
Решите уравнение 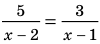
Решение:
► ОДЗ: 
На этой ОДЗ данное уравнение равносильно уравнениям:
то есть
Учтем ОДЗ. При
Таким образом, 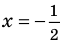
Ответ:
Используем равносильные преобразования для решения данного уравнения. Для этого необходимо учесть ОДЗ, поэтому зафиксируем ее ограничения в начале решения.
Укажем, что в уравнениях ограничения ОДЗ можно только зафиксировать, но не решать, а в конце проверить, выполняются ли эти ограничения для найденных корней.
При переносе члена данного уравнения из одной части уравнения в другую с противоположным знаком получаем уравнение (1), равносильное заданному.
Приводя к общему знаменателю, раскрывая скобки и приводя подобные члены, снова получаем верное равенство и можем обосновать, что при выполнении обратных действий равенство также не нарушается, таким образом, полученные уравнения (1)-(3) равносильны заданному (на его ОДЗ).
Дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю. Но второе условие уже учтено в ограничениях ОДЗ, таким образом, получаем уравнение (4), равносильное заданному уравнению на его ОДЗ. Поскольку все преобразования были равносильными только с учетом ОДЗ, то мы должны проверить, удовлетворяет ли полученное число ограничениям ОДЗ.
Причины появления посторонних корней и потери корней при решении уравнений
Наиболее типичные случаи появления посторонних корней и потери корней приведены в таблице 9. Там же указано, как в каждом из этих случаев получить правильное (или полное) решение.
Применение свойств функций к решению уравнений
1. Конечная ОДЗ
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
Пример:
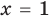
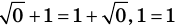
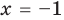
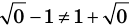
2. Оценка левой и правой частей уравнения
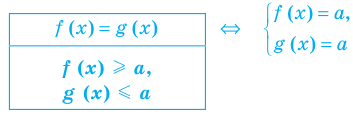
Если надо решить уравнение вида 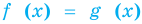


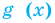
Пример:
►
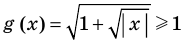
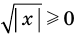
Итак, заданное уравнение равносильно системе
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю
Пример:
►
Итак, заданное уравнение равносильно системе
Из первого уравнения получаем 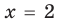
3. Использование возрастания и убывания функций
Схема решения уравнения
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку левой и правой частей уравнения)
Теоремы о корнях уравнения
Если в уравнении 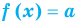
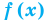
Пример:
Уравнение 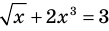
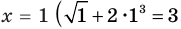
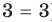
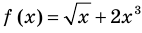
Если в уравнении 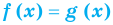
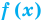
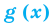
Пример:
Уравнение 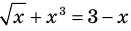
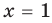
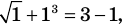
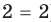
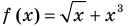

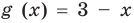
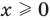
Объяснение и обоснование:
Конечная ОДЗ
Напомним, что в случае, когда дано уравнение 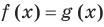
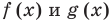
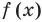
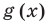
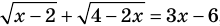
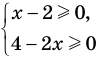
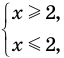


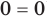


Рассмотренный пример позволяет выделить ориентир для решения аналогичных уравнений:
если ОДЗ уравнения (а также неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Замечание. В том случае, когда ОДЗ — пустое множество (не содержит ни одного числа), мы можем сразу дать ответ, что данное уравнение не имеет корней.
Например, если необходимо решить уравнение 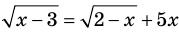
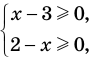
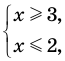
Оценка левой и правой частей уравнения
Некоторые уравнения можно решить с помощью оценки левой и правой частей уравнения.
Пусть дано уравнение 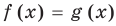
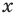
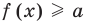
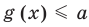
Рассмотрим два случая:
Если 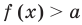
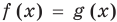
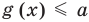
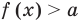
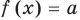
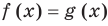
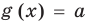
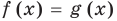
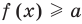
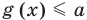
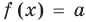
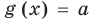
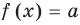
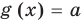
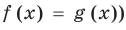
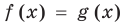
Коротко это можно записать так:
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 10.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения 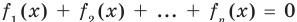
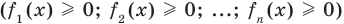
Если предположить, что 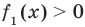

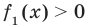
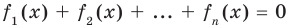
Например, чтобы решить уравнение 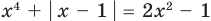
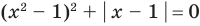
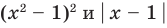
Из второго уравнения получаем 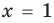
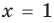
Использование возрастания и убывания функций к решению уравнений
Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения.
Полезно помнить специальные теоремы о корнях уравнения.
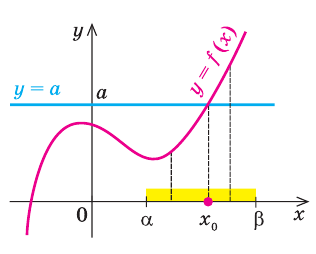
Теорема 1. Если в уравнении 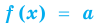
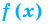
Графически утверждение теоремы проиллюстрировано на рисунке 52. Прямая 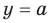
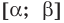
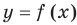
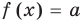
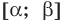
• Если на промежутке 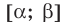
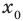
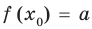
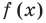
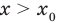
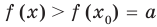
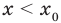
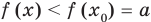
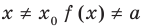
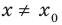
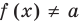
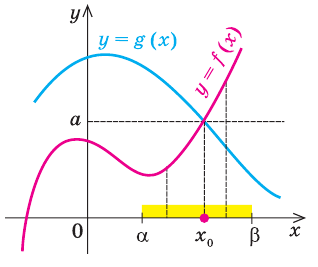
Теорема 2. Если в уравнении 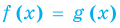
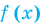
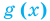
Графически утверждение теоремы проиллюстрировано на рисунке 53.
• Если на промежутке 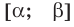
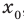
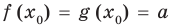
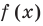
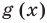
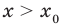
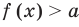
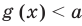
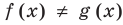
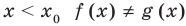
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение 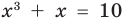
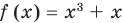

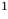
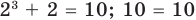
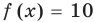
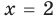
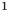

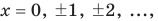
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Пример:
Решим с помощью теоремы 2 уравнение 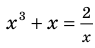
► Сначала следует учесть его ОДЗ: 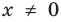
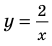
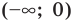
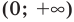
1) При 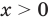
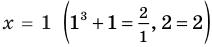
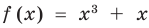

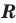
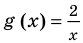

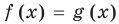
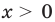
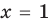
2) При 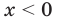
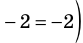
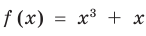
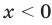
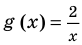
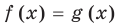
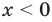
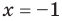
Примеры решения задач:
Пример №424
Решите уравнение 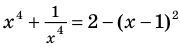
Решение:
► ОДЗ: 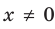
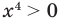
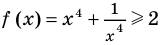
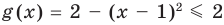
Таким образом, данное уравнение равносильно системе 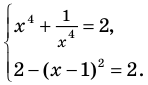


Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ 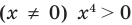
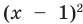
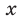
Пример №425
Решите систему уравнений
Решение:
► ОДЗ: 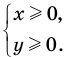
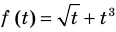
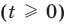
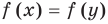
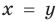
Подставляя 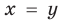
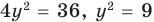
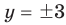

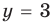
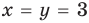
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство 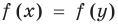
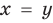
Замечание. Утверждение, обоснованное в комментарии к задаче 2, может быть использовано при решении аналогичных задач. Коротко его можно сформулировать так: если функция 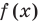
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:ОБЛАСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ 9 и 8 класс ООФСкачать

Как найти область определения функции?
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно углубить знания данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y = x + x — 2 или y = 5 · x 2 + 1 · x 3 , y = x x — 5 или y = x — 1 5 — 3 . Рассмотрим теорию и решим несколько примеров с подобными заданиями.
Видео:Область определения (корня) функции #2. Алгебра 10 класс.Скачать

Что значит найти область определения
После того, как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y = f ( x ) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Видео:Область определения тригонометрических функцийСкачать

Ограничение области определения
Область определения рассматривается еще в школьной курсе. у действительных чисел она может быть ( 0 , + ∞ ) или такой [ − 3 , 1 ) ∪ [ 5 , 7 ) . Еще по виду функции можно визуально определить ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y = x + 2 · x x 4 — 1 ;
- при наличии переменной под знаком корня необходимо обращать внимание на корень четной степени типа y = x + 1 или y = 2 3 · x + 3 x ;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y = 5 · ( x + 1 ) — 3 , y = — 1 + x 1 1 3 , y = ( x 3 — x + 1 ) 2 , которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y = ln x 2 + x 4 или y = 1 + log x — 1 ( x + 1 ) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y = x 3 + t g 2 · x + 5 или y = c t g ( 3 · x 3 — 1 ) , так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y = a r c sin ( x + 2 ) + 2 · x 2 , y = a r c cos x — 1 + x , область определения которых определяется ни интервале от — 1 до 1 .
При отсутствии хотя бы одного признака, область определения приходится искать другим образом. Рассмотрим пример функции вида y = x 4 + 2 · x 2 — x + 1 2 + 2 2 3 · x . Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Видео:ГРАФИК ФУНКЦИИ 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать
Правила нахождения области определения
Для примера рассмотрим функцию типа y = 2 · x + 1 . Для вычисления ее значения можем определить x . Из выражения 2 · x + 1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y = 3 x — 1 , а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3 x — 1 знаменатель равняется нулю при х = 1 , поэтому искомая область определения данной функции примет вид ( − ∞ , 1 ) ∪ ( 1 , + ∞ ) и считается числовым множеством.
На рассмотрении примера y = x 2 — 5 · x + 6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x 2 − 5 · x + 6 ≥ 0 . После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как ( − ∞ , 2 ] ∪ [ 3 , + ∞ ) .
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Видео:Найти область определения функции - bezbotvyСкачать

Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно, чтобы имело место следующее утверждение:
Когда функция f f считается суммой n функций f 1 , f 2 , … , f n , иначе говоря, эта функция задается при помощи формулы y = f 1 ( x ) + f 2 ( x ) + … + f n ( x ) , тогда ее область определения считается пересечением областей определения функций f 1 , f 2 , … , f n . Данное утверждение можно записать как:
D ( f ) = D ( f 1 ) D ( f 2 ) . . . D ( f n )
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом для понимания перечисления числовых множеств.
Найти область определения функции вида y = x 7 + x + 5 + t g x .
Заданная функция представляется как сумма четырех: степенной с показателем 7 ,степенной с показателем 1 , постоянной, функции тангенса.
По таблице определения видим, что D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = ( − ∞ , + ∞ ) , D ( f 3 ) = ( − ∞ , + ∞ ) , причем область определения тангенса включает в себя все действительные числа, кроме π 2 + π · k , k ∈ Z .
Областью определения заданной функции f является пересечение областей определения f 1 , f 2 , f 3 и f 4 . То есть для функции существует такое количество действительных чисел, куда не входит π 2 + π · k , k ∈ Z .
Ответ: все действительные числа кроме π 2 + π · k , k ∈ Z .
Для нахождения области определения произведения функций необходимо применять правило:
Когда функция f считается произведением n функций f 1 , f 2 , f 3 и f n , тогда существует такая функция f , которую можно задать при помощи формулы y = f 1 ( x ) · f 2 ( x ) · … · f n ( x ) , тогда ее область определения считается областью определения для всех функций.
Запишется D ( f ) = D ( f 1 ) D ( f 2 ) . . . D ( f n )
Найти область определения функции y = 3 · a r c t g x · ln x .
Правая часть формулы рассматривается как f 1 ( x ) · f 2 ( x ) · f 3 ( x ) , где за f 1 является постоянной функцией, f 2 является арктангенсом, f 3 – логарифмической функцией с основанием e . По условию имеем, что D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = ( − ∞ , + ∞ ) и D ( f 3 ) = ( 0 , + ∞ ) . Мы получаем, что
D ( f ) = D ( f 1 ) D ( f 2 ) D ( f n ) = ( — ∞ , + ∞ ) ( — ∞ , + ∞ ) D ( 0 , + ∞ ) = ( 0 , + ∞ )
Ответ: область определения y = 3 · a r c t g x · ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y = C · f ( x ) , где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y = C · f ( x ) – произведение постоянной функции и f . Область определения – это все действительные числа области определения D ( f ) . Отсюда видим, что область определения функции y = C · f ( x ) является — ∞ , + ∞ D ( f ) = D ( f ) .
Получили, что область определения y = f ( x ) и y = C · f ( x ) , где C является некоторое действительное число, совпадают. Это видно на примере определения корня y = x считается [ 0 , + ∞ ) , потому как область определения функции y = — 5 · x — [ 0 , + ∞ ) .
Области определения y = f ( x ) и y = − f ( x ) совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Найти область определения функции y = log 3 x − 3 · 2 x .
Необходимо рассмотреть как разность двух функций f 1 и f 2 .
f 1 ( x ) = log 3 x и f 2 ( x ) = 3 · 2 x . Тогда получим, что D ( f ) = D ( f 1 ) D ( f 2 ) .
Область определения записывается как D ( f 1 ) = ( 0 , + ∞ ) . Приступим к области определения f 2 . в данном случае она совпадает с областью определения показательной, тогда получаем, что D ( f 2 ) = ( − ∞ , + ∞ ) .
Для нахождения области определения функции y = log 3 x − 3 · 2 x получим, что
D ( f ) = D ( f 1 ) D ( f 2 ) = ( 0 , + ∞ ) — ∞ , + ∞
Необходимо озвучить утверждение о том, что областью определения y = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 является множество действительных чисел.
Рассмотрим y = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 , где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы ( n + 1 ) -ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R .
Найти область определения f 1 ( x ) = x 5 + 7 x 3 — 2 x 2 + 1 2 .
Примем обозначение f за разность двух функций, тогда получим, что f 1 ( x ) = x 5 + 7 x 3 — 2 x 2 + 1 2 и f 2 ( x ) = 3 · x — ln 5 . Выше было показано, что D ( f 1 ) = R . Область определения для f 2 является совпадающей со степенной при показателе – ln 5 , иначе говоря, что D ( f 2 ) = ( 0 , + ∞ ) .
Получаем, что D ( f ) = D ( f 1 ) D ( f 2 ) = — ∞ , + ∞ ( 0 , + ∞ ) = ( 0 , + ∞ ) .
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y = f 1 ( f 2 ( x ) ) . Известно, что D ( f ) является множеством всех x из определения функции f 2 , где область определения f 2 ( x ) принадлежит области определения f 1 .
Видно, что область определения сложной функции вида y = f 1 ( f 2 ( x ) ) находится на пересечении двух множеств таких, где x ∈ D ( f 2 ) и f 2 ( x ) ∈ D ( f 1 ) . В стандартном обозначении это примет вид
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 )
Рассмотрим решение нескольких примеров.
Найти область определения y = ln x 2 .
Данную функцию представляем в виде y = f 1 ( f 2 ( x ) ) , где имеем, что f 1 является логарифмом с основанием e , а f 2 – степенная функция с показателем 2 .
Для решения необходимо использовать известные области определения D ( f 1 ) = ( 0 , + ∞ ) и D ( f 2 ) = ( − ∞ , + ∞ ) .
Тогда получим систему неравенств вида
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 ) ⇔ x ∈ — ∞ , + ∞ x 2 ∈ ( 0 , + ∞ ) ⇔ ⇔ x ∈ ( — ∞ , + ∞ ) x 2 > 0 ⇔ x ∈ ( — ∞ , + ∞ ) x ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ ⇔ x ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ )
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Найти область определения функции y = ( a r c sin x ) — 1 2 .
Так как дана сложная функция, необходимо рассматривать ее как y = f 1 ( f 2 ( x ) ) , где f 1 является степенной функцией с показателем — 1 2 , а f 2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D ( f 1 ) = ( 0 , + ∞ ) и D ( f 2 ) = [ − 1 , 1 ] . Теперь найдем все множества значений x , где x ∈ D ( f 2 ) и f 2 ( x ) ∈ D ( f 1 ) . Получаем систему неравенств вида
x ∈ D ( f 2 ) f 2 ( x ) ∈ D ( f 1 ) ⇔ x ∈ — 1 , 1 a r c sin x ∈ ( 0 , + ∞ ) ⇔ ⇔ x ∈ — 1 , 1 a r c sin x > 0
Для решения a r c sin x > 0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [ − 1 , 1 ] , причем обращается в ноль при х = 0 , значит, что a r c sin x > 0 из определения x принадлежит промежутку ( 0 , 1 ] .
Преобразуем систему вида
x ∈ — 1 , 1 a r c sin x > 0 ⇔ x ∈ — 1 , 1 x ∈ ( 0 , 1 ] ⇔ x ∈ ( 0 , 1 ]
Область определения искомой функции имеет интервал равный ( 0 , 1 ] .
Ответ: ( 0 , 1 ] .
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y = f 1 ( f 2 ( … f n ( x ) ) ) ) . Область определения такой функции ищется из x ∈ D ( f n ) f n ( x ) ∈ D ( f n — 1 ) f n — 1 ( f n ( x ) ) ∈ D ( f n — 2 ) . . . f 2 ( f 3 ( . . . ( f n ( x ) ) ) ∈ D ( f 1 ) .
Найти область определения y = sin ( l g x 4 ) .
Заданная функция может быть расписана, как y = f 1 ( f 2 ( f 3 ( x ) ) ) , где имеем f 1 – функция синуса, f 2 – функция с корнем 4 степени, f 3 – логарифмическая функция.
Имеем, что по условию D ( f 1 ) = ( − ∞ , + ∞ ) , D ( f 2 ) = [ 0 , + ∞ ) , D ( f 3 ) = ( 0 , + ∞ ) . Тогда областью определения функции – это пересечение множеств таких значений, где x ∈ D ( f 3 ) , f 3 ( x ) ∈ D ( f 2 ) , f 2 ( f 3 ( x ) ) ∈ D ( f 1 ) . Получаем, что
x ∈ D ( f 3 ) f 3 ( x ) ∈ D ( f 2 ) f 2 ( f 3 ( x ) ) ∈ D ( f 1 ) ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x 4 ∈ — ∞ , + ∞
Условие lg x 4 ∈ — ∞ , + ∞ аналогично условию l g x ∈ [ 0 , + ∞ ) , значит
x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x 4 ∈ — ∞ , + ∞ ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) ⇔ ⇔ x ∈ ( 0 , + ∞ ) lg x ∈ [ 0 , + ∞ ) ⇔ x ∈ ( 0 , + ∞ ) lg x ≥ 0 ⇔ ⇔ x ∈ ( 0 , + ∞ ) lg x ≥ lg 1 ⇔ x ∈ ( 0 , + ∞ ) x ≥ 1 ⇔ ⇔ x ∈ [ 1 , + ∞ )
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f 1 ( x ) f 2 ( x ) . Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f 2 ( х ) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Запишем функцию y = f 1 ( x ) f 2 ( x ) в виде y = f 1 ( x ) · ( f 2 ( x ) ) — 1 . Тогда получим произведение функций вида y = f 1 ( x ) с y = ( f 2 ( x ) ) — 1 . Областью определения функции y = f 1 ( x ) является множество D ( f 1 ) , а для сложной y = ( f 2 ( x ) ) — 1 определим из системы вида x ∈ D ( f 2 ) f 2 ( x ) ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Значит, x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ∈ ( — ∞ , 0 ) ∪ ( 0 , + ∞ ) ⇔ x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 .
Найти область определения y = t g ( 2 · x + 1 ) x 2 — x — 6 .
Заданная функция дробная, поэтому f 1 – сложная функция, где y = t g ( 2 · x + 1 ) и f 2 – целая рациональная функция, где y = x 2 − x − 6 , а область определения считается множеством всех чисел. Можно записать это в виде
x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0
Представление сложной функции y = f 3 ( f 4 ( x ) ) , где f 3 –это функция тангенс, где в область определения включены все числа, кроме π 2 + π · k , k ∈ Z , а f 4 – это целая рациональная функция y = 2 · x + 1 с областью определения D ( f 4 ) = ( − ∞ , + ∞ ) . После чего приступаем к нахождению области определения f 1 :
x ∈ D ( f 4 ) 2 · x + 1 ∈ D ( f 3 ) ⇔ x ∈ ( — ∞ , + ∞ ) 2 x + 1 ≠ π 2 + π · k , k ∈ Z ⇔ x ≠ π 4 — 1 2 + π 2 · k , k ∈ Z
Еще необходимо рассмотреть нижнюю область определения y = t g ( 2 · x + 1 ) x 2 — x — 6 . Тогда получаем, что
x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 2 ( x ) ≠ 0 ⇔ x ≠ π 4 — 1 2 + π 2 · k , k ∈ Z x ∈ — ∞ , + ∞ x 2 — x — 6 ≠ 0 ⇔ ⇔ x ≠ π 4 — 1 2 + π 2 · k , k ∈ Z x ≠ — 2 x ≠ 3
Ответ: множество действительных чисел, кроме — 2 , 3 и π 4 — 1 2 + π 2 · k , k ∈ Z .
Область определения логарифма с переменной в основании
Определение логарифма существует для положительных оснований не равных 1 . Отсюда видно, что функция y = log f 2 ( x ) f 1 ( x ) имеет область определения, которая выглядит так:
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
А аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y = log a f 1 ( x ) log a f 2 ( x ) , a > 0 , a ≠ 1 . После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y = log a f 1 ( x ) и y = log a f 2 ( x ) можно определить из получившейся системы вида x ∈ D ( f 1 ) f 1 ( x ) > 0 и x ∈ D ( f 2 ) f 2 ( x ) > 0 . Иначе эту область можно записать в виде y = log a f 1 ( x ) log a f 2 ( x ) , a > 0 , a ≠ 1 , что означает нахождение y = log f 2 ( x ) f 1 ( x ) из самой системы вида
x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 log a f 2 ( x ) ≠ 0 = x ∈ D ( f 1 ) f 1 ( x ) > 0 x ∈ D ( f 2 ) f 2 ( x ) > 0 f 2 ( x ) ≠ 1
Обозначить область определения функции y = log 2 · x ( x 2 — 6 x + 5 ) .
Следует принять обозначения f 1 ( x ) = x 2 − 6 · x + 5 и f 2 ( x ) = 2 · x , отсюда D ( f 1 ) = ( − ∞ , + ∞ ) и D ( f 2 ) = ( − ∞ , + ∞ ) . Необходимо приступить к поиску множества x , где выполняется условие x ∈ D ( f 1 ) , f 1 ( x ) > 0 , x ∈ D ( f 2 ) , f 2 ( x ) > 0 , f 2 ( x ) ≠ 1 . Тогда получаем систему вида
x ∈ ( — ∞ , + ∞ ) x 2 — 6 x + 5 > 0 x ∈ ( — ∞ , + ∞ ) 2 · x > 0 2 · x ≠ 1 ⇔ x ∈ ( — ∞ , + ∞ ) x ∈ ( — ∞ , 1 ) ∪ ( 5 , + ∞ ) x ∈ ( — ∞ , + ∞ ) x > 0 x ≠ 1 2 ⇔ ⇔ x ∈ 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ )
Отсюда видим, что искомой областью функции y = log 2 · x ( x 2 — 6 x + 5 ) считается множнство, удовлетворяющее условию 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ ) .
Ответ: 0 , 1 2 ∪ 1 2 , 1 ∪ ( 5 , + ∞ ) .
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y = ( f 1 ( x ) ) f 2 ( x ) . Ее область определения включает в себя такие значения x , которые удовлетворяют системе x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 1 ( x ) > 0 .
Эта область позволяет переходить от показательно-степенной к сложной вида y = a log a ( f 1 ( x ) ) f 2 ( x ) = a f 2 ( x ) · log a f 1 ( x ) , где где a > 0 , a ≠ 1 .
Найти область определения показательно-степенной функции y = ( x 2 — 1 ) x 3 — 9 · x .
Примем за обозначение f 1 ( x ) = x 2 − 1 и f 2 ( x ) = x 3 — 9 · x .
Функция f 1 определена на множестве действительных чисел, тогда получаем область определения вида D ( f 1 ) = ( − ∞ , + ∞ ) . Функция f 2 является сложной, поэтому ее представление примет вид y = f 3 ( f 4 ( x ) ) , а f 3 – квадратным корнем с областью определения D ( f 3 ) = [ 0 , + ∞ ) , а функция f 4 – целой рациональной, D ( f 4 ) = ( − ∞ , + ∞ ) . Получаем систему вида
x ∈ D ( f 4 ) f 4 ( x ) ∈ D ( f 3 ) ⇔ x ∈ ( — ∞ , + ∞ ) x 3 — 9 · x ≥ 0 ⇔ ⇔ x ∈ ( — ∞ , + ∞ ) x ∈ — 3 , 0 ∪ [ 3 , + ∞ ) ⇔ x ∈ — 3 , 0 ∪ [ 3 , + ∞ )
Значит, область определения для функции f 2 имеет вид D ( f 2 ) = [ − 3 , 0 ] ∪ [ 3 , + ∞ ) . После чего необходимо найти область определения показательно-степенной функции по условию x ∈ D ( f 1 ) x ∈ D ( f 2 ) f 1 ( x ) > 0 .
Получаем систему вида x ∈ — ∞ , + ∞ x ∈ — 3 , 0 ∪ [ 3 , + ∞ ) x 2 — 1 > 0 ⇔ x ∈ — ∞ , + ∞ x ∈ — 3 , 0 ∪ [ 3 , + ∞ ) x ∈ ( — ∞ , — 1 ) ∪ ( 1 , + ∞ ) ⇔ ⇔ x ∈ — 3 , — 1 ∪ [ 3 , + ∞ )
Ответ: [ − 3 , − 1 ) ∪ [ 3 , + ∞ )
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.Ф
| Функция | Ее область определения | ||||||||||||||||
| Функция | Ее область определения |
| R | |
| Линейная y = k · x + b | R |
| — ∞ , 0 ∪ 0 , + ∞ | |
| Квадратичная y = a · x 2 + b · x + c | R |
| y = a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 | R |
| Целая рациональная | R |
| y = C · f ( x ) , где C — число | D ( f ) |
| y = f ( x ) n , где n — четное | x ∈ D ( f 1 ) , f ( x ) ≥ 0 |
| Показательно-степенная y = ( f 1 ( x ) ) f 2 ( x ) | x ∈ D ( f 1 ) , x ∈ D ( f 2 ) , f 1 ( x ) > 0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y = x 2 — 4 x — 2 и y = x + 2 являются разными функциями, так как первая определяется на ( − ∞ , 2 ) ∪ ( 2 , + ∞ ) , а вторая из множества действительных чисел. Из преобразования y = x 2 — 4 x — 2 = x — 2 x + 2 x — 2 = x + 2 видно, что функция имеет смысл при x ≠ 2 .

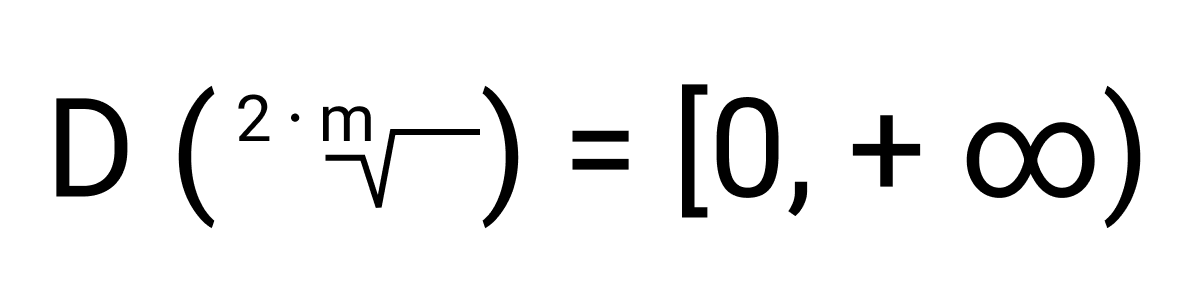
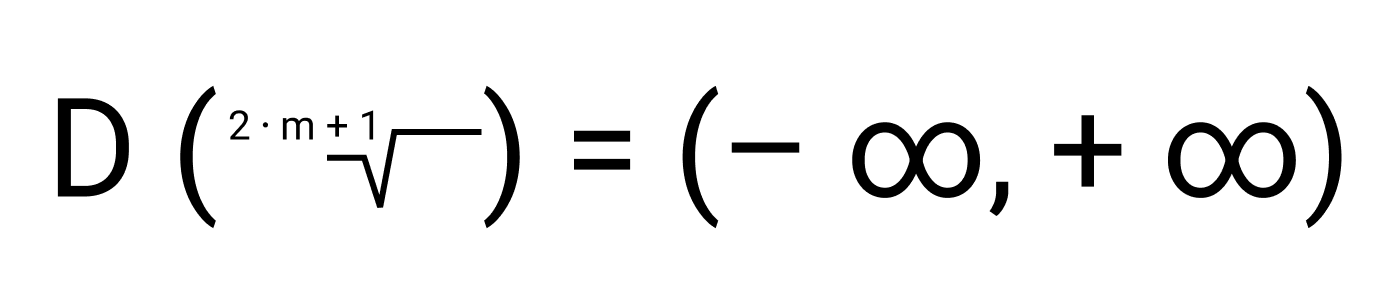


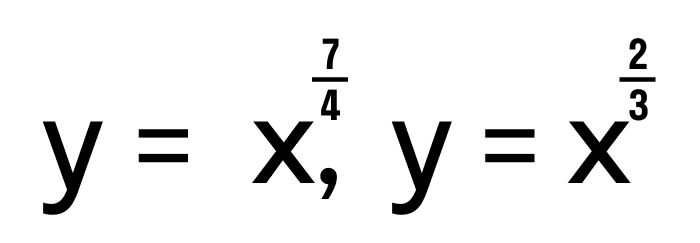 определены на интервале [0, +∞), так как их показатели положительные, но не целые.
определены на интервале [0, +∞), так как их показатели положительные, но не целые.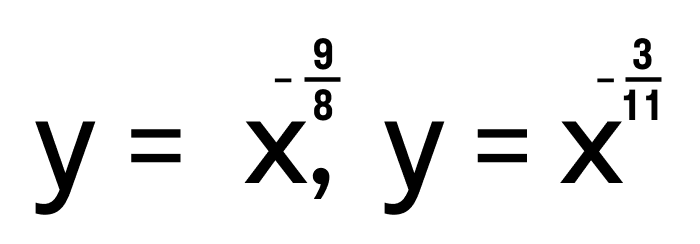 — открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.
— открытый числовой луч (0, +∞), так как их показатели не целые и отрицательные.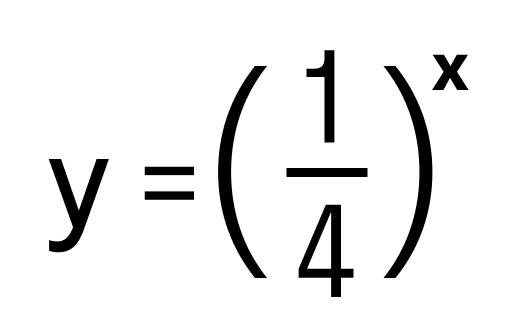
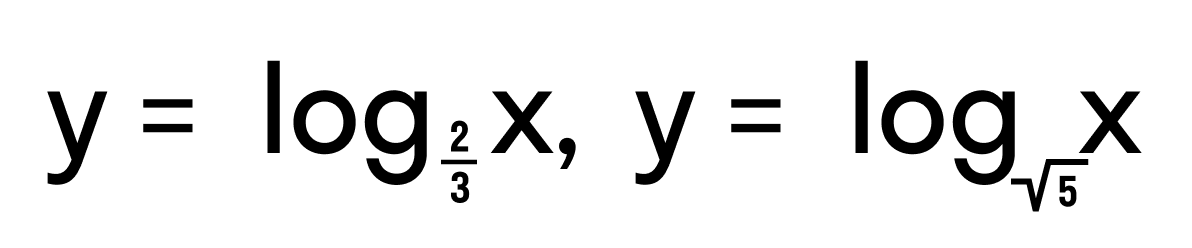



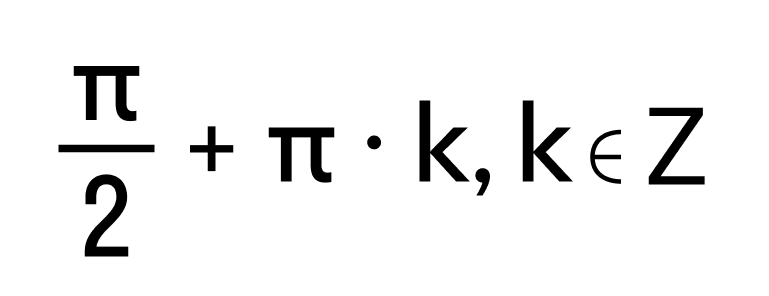 . Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.
. Область определения котангенса — это множество всех действительных чисел, кроме чисел πk, k ∈ Z.