- Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
- Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
- Выражения и уравнения — определение и вычисление с примерами решения
- Выражения и уравнения
- Правила раскрытия скобок
- Уравнения. Основные свойства уравнений
- Основные свойства уравнений
- Применение уравнений к решению задач
- Перпендикулярные и параллельные прямые
- Перпендикулярные прямые
- Параллельные прямые
- Координатная плоскость
- Графики зависимостей между величинами
- Алгоритм расчёта вещественных корней полиномов
- Литература
- 🎬 Видео
Видео:6.3 Квадратное уравнение. "Поколение Python": курс для начинающих. Курс StepikСкачать

Решения кубических уравнений с вещественными коэффициентами. Универсальные методы. Дискриминант кубического уравнения. Формула Виета для кубического уравнения.
Кубическим уравнением называется уравнение вида
- ax 3 + bx 2 + cx +d = 0 , (1)
- где a, b,c ,d — постоянные коэффициенты, а х — переменная.
Мы рассмотрим случай, когда коэффициенты являются веществеными числами.
Корни кубического уравнения. Нахождение корней (решение) кубического уравнения.
Число х называется корнем кубического уравнения (1), если при его подстановке уравнение (1) обращается в верное равенство.
Кубическое уравнение имеет не более трех корней (над комплексным полем всегда три корня, с учетом кратности) . И всегда имеет хотя бы 1 (вещественный) корень. Все возможные случаи состава корней легко определить с помощью знака дискриминанта кубического уравнения, т.е.:
Δ= -4b 3 d + b 2 c 2 — 4ac 3 + 18abcd — 27a 2 d 2 (Да, это дискриминант кубического уравнения)
Итак, возможны только 3 следующих случая:
- Δ > 0 — тогда уравнение имеет 3 различных корня. (Для продвинутых — три различных вещественных корня)
- Δ 3 + py + q = 0 (2)
К такому виду можно привести любое кубическое уравнение вида (1) с помощью следующей замены:
- x= y — b/3a (3)
- p= — b 2 /3a 2 + c/a
- q= 2b 3 /27a 3 — bc/3a 2 + d/a
Итак, приступим к вычислению корней. Найдем следующие величины:
Дискриминант уравнения (2) в этом случае равен
Дискриминант исходного уравнения (1) будет иметь тот же знак , что и вышеуказанный дискриминант. Корни уравнения (2) выражаются следующим образом:
Соответственно, если Q>0, то уравнения (2) и (1) будут иметь лишь 1 (вещественный) корень, y1. Подставим его в (3) и найдем х для уравнения (1). (если вас интересуют также мнимые корни, то просто вычислите еще и y2, y3 и подставьте их в (3).
Если Q 3 + ax 2 + bx +c = 0 (4)
Очевидно, любое уравнение вида (1) можно привести к виду (4), просто поделив его на коэффициент а.
Итак, алгоритм применения этой формулы:
3. a) Если S>0, то вычисляем
И наше уравнение имеет 3 корня (вещественных):
Тогда единственный корень (вещественный): x1= -2sgn(R)*|Q| 1/2 *ch(φ) — a/3
Для тех, кого интересуют также и мнимые корни:
- ch(x)=(e x +e -x )/2
- Arch(x) = ln(x + (x 2 -1) 1/2 )
- sh(x)=(e x -e -x )/2
- sgn(x) — знак х
в) Если S=0,то уравнение имеет меньше трех различных решений:
Консультации и техническая
поддержка сайта: Zavarka Team
Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Выражения и уравнения — определение и вычисление с примерами решения
Содержание:
Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Выражения и уравнения
Вы уже знаете, что такое буквенные выражения, и умеете их упрощать с помощью законов сложения и умножения. Например,
Пример:
Есть ли коэффициент в выражении 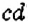
Вспомним, что преобразование выражения со скобками в выражение без скобок называется раскрытием скобок. Например:
Обратным действием в этом примере является вынесение общего множителя за скобки.
Слагаемые, содержащие одинаковые буквенные множители, называют подобными слагаемыми. С помощью вынесения общего множителя за скобки сводят подобные слагаемые:
Правила раскрытия скобок
Правила раскрытия скобок
- Если перед скобками стоит знак
, то при раскрытии скобок знаки слагаемых в скобках сохраняют;
- Если перед скобками стоит знак
, то при раскрытии скобок знаки слагаемых в скобках изменяют на противоположные.
Пример:
Упростите выражение: 1) 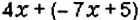
Решение:
1. Перед скобками стоит знак 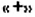
2. Перед скобками стоит знак 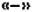
Для раскрытия скобок используют распределительное свойство умножения: 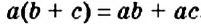
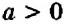
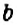
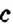
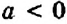
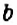
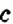
Пример:
Упростите выражение: 1) 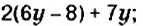
Решение:
1. Множитель 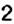
2. Множитель 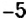
- Слово «сумма» происходит от латинского summа, что значит «итог», «общее количество».
- Слово «плюс» происходит от латинского plus, что значит «больше», а слово «минус» — от латинского minus, что значит «меньше». Знаки
и
используют для обозначения действий сложения и вычитания. Эти знаки ввёл чешский учёный И. Видман в 1489 г в книге «Быстрый и приятный счёт для всех торговцев»(рис. 138).
Уравнения. Основные свойства уравнений
Вы уже знаете, что такое уравнение, корень уравнения. Вспомним основные формулировки.
Определение:
Уравнением называется равенство, содержащее неизвестное, значение которого нужно найти.
Неизвестное число в уравнении обозначают буквой 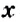
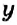
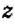
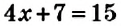
уравнением, где 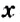
Определение:
Значение неизвестного, обращающее уравнение в верное числовое равенство, называется корнем уравнения.
Так, корнем уравнения 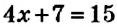
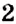
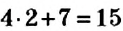
Уравнение может иметь больше одного корня. Например, уравнение 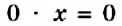
Уравнение может не иметь корней. Например, уравнение 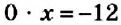
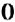
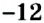
Определение:
Решить уравнение — значит найти все его корни или установить, что уравнение не имеет ни одного корня.
В 5 классе вы находили корень уравнения как неизвестный компонент арифметического действия. При решении более сложных уравнений опираются на свойства равенств. Рассмотрим основные из них.
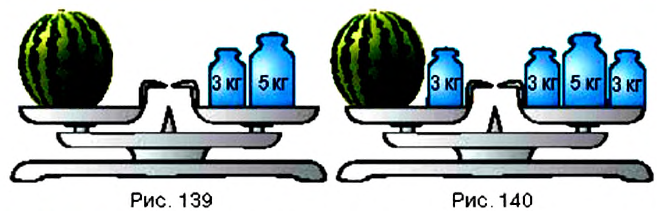
Посмотрите на рисунок 139. Вы видите, что на левой чаше весов находится арбуз неизвестной массы, а на правой — гири массой 5 кг и 3 кг. Если на обе чаши весов положить по гире массой 3 кг, то весы останутся в равновесии (рис. 140). Понятно, что, сняв эти гири или поставив навесы одинаковые гири другой массы, снова получим равновесие на весах. Этот пример иллюстрирует следующее свойство равенств.
Определение: Если к обеим частям равенства прибавить (из обеих частей равенства вычесть) одно и то же число, то равенство не изменится.
Пример:
Решите уравнение: 1) 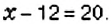
Решение:
К левой и правой частям уравнения прибавим число 12 и упростим полученное равенство:
Решая уравнение, в левой его части «уединили неизвестное». Такой же результат получим, если число 12 перенесём из левой части в правую, изменив при этом его знак.
Определение:
Слагаемое можно переносить из одной части уравнения в другую, изменяя знак этого слагаемого на противоположный.
Пример:
Можно ли переносить в другую часть уравнения слагаемое, содержащее неизвестное? Да.
Посмотрите на рисунок 141. Вы видите, что масса пакета муки равна 2 кг. Понятно, что масса трёх таких пакетов втрое больше (рис. 142). Этот пример иллюстрирует другое свойство равенств.
Определение: Если обе части равенства умножить (разделить) на одно и то же число, отличное от нуля, то равенство не изменится. 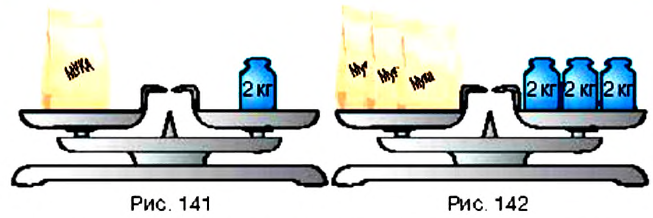
Пример:
Решите уравнение
Решение:
Чтобы избавиться от дробного коэффициента, умножим на 3 обе части уравнения:
Основные свойства уравнений
Основные свойства уравнений
- Корни уравнения не изменятся, если к обеим частям уравнения прибавить (из обеих частей уравнения вычесть) одно и то же число.
- Корни уравнения не изменятся, если обе части уравнения умножить (разделить) на одно и то же число, отличное от нуля.
Считают, что язык алгебры — это уравнения. «Чтобы решить вопросы. относящиеся к числам или к абстрактным отношениям величин, нужно лишь перевести задачу с родного языка на язык алгебраический», — писал великий И. Ньютон (1643-1727) в своём учебнике по алгебре, названном «Общая арифметика».
Применение уравнений к решению задач
В 5 классе с помощью уравнений вы решали задачи на нахождение суммы двух величин или их разности.
В 6 классе будем рассматривать особый вид задач — на равенство двух величин. В таких задачах тоже сравнивают две величины, например, количество книг на первой и второй полках. Значения же выражений с этими двумя величинами приравнивают.
Пример:
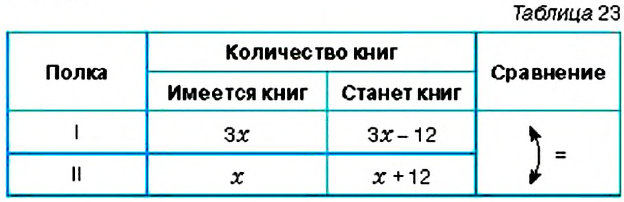
На первой полке книг в 3 раза больше, чем на второй. Если с первой полки переставить на вторую 12 книг, то на обеих полках их станет поровну. Сколько книг на каждой полке?
Решение:
Составим краткую запись задачи в виде таблицы 23
Пусть 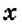
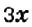
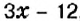
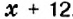
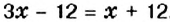
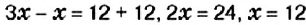

Первым произведением, содержащим исследование алгебраических вопросов, считают трактат «Арифметика» Диофанта (середина IV в.). Из 13 книг, составляющих полное собрание трудов Диофанта, до нас дошло только 6. В них предложено решение сложных алгебраических задач. Основная часть трактата — сборник задач (в первых шести книгах их 189) с решениями и удачно подобранными иллюстрациями к способам решения.
Перпендикулярные и параллельные прямые
Вы знаете, что прямая — это геометрическая фигура. Две прямые могут по-разному размещаться на плоскости. В 6 классе вы узнаете о перпендикулярных и параллельных прямых.
Перпендикулярные прямые
Посмотрите па перекрёсток дорог на рисунке 143. Вы видите, что дороги напоминают пересекающиеся прямые, которые образуют четыре прямых угла. В этом случае говорят, что прямые пересекаются под прямым углом. В тетради по математике клеточки образуются перпендикулярными прямыми.
Определение:
Две прямые на плоскости называются перпендикулярными, если они пересекаются под прямым углом.
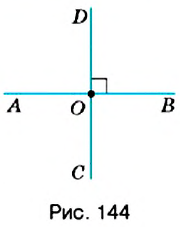
На рисунке 144 изображены прямые 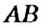
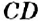

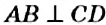
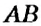
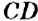
Если прямая 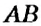
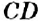

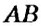
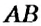
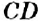
Пример:
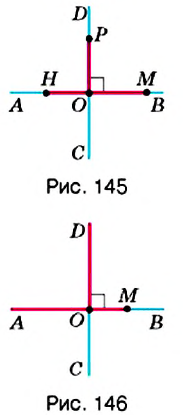
Бывают ли перпендикулярными отрезки? лучи? Да, если они являются частями соответствующих перпендикулярных прямых (рис. 145—146).
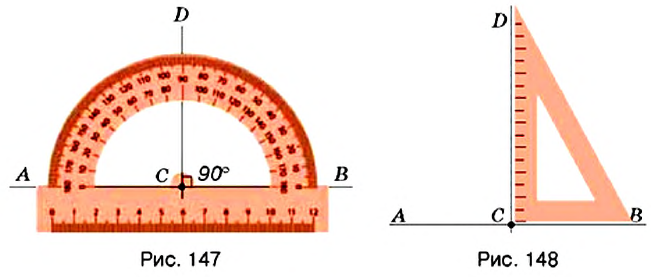
Для построения перпендикулярных прямых используют транспортир или угольник. На рисунке 147 вы видите, как строили прямую 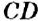

Параллельные прямые
Посмотрите на рисунок 149. Вы видите рельсы трамвайных путей, напоминающие прямые, которые лежат в одной плоскости и не пересекаются. Это пример параллельных прямых. Вокруг нас много других примеров параллельных прямых. Так, в тетради в клеточку горизонтальные линии параллельны. То же самое можно сказать и про вертикальные линии. Противоположные края парты, противоположные стороны оконной рамы, троллейбусные штанги также параллельны.
Определение:
Две прямые на плоскости называются параллельными, если они не пересекаются.
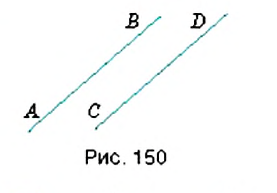
На рисунке 150 изображены параллельные прямые 


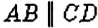


Если прямая 



Пример:
Бывают ли параллельными лучи? отрезки? Да, если они являются частями соответствующих параллельных прямых.
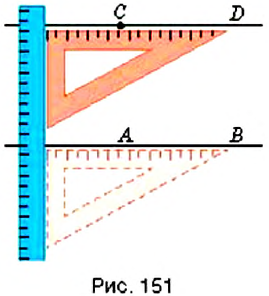
На рисунке 151 вы видите, как с помощью линейки и угольника через точку 


Название «перпендикулярный» происходит от латинского слова «perpendicufaris», которое означает «отвесный». Знак 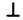
Название «параллельный» происходит от греческого слова «раralelos» — «идущий рядом». Символ параллельности 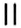
Координатная плоскость
Вы уже знаете, что такое координатная прямая (рис. 162). На ней точка 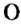
Однако на практике часто приходится пользоваться ориентирами не только вдоль прямой, но и на плоскости.
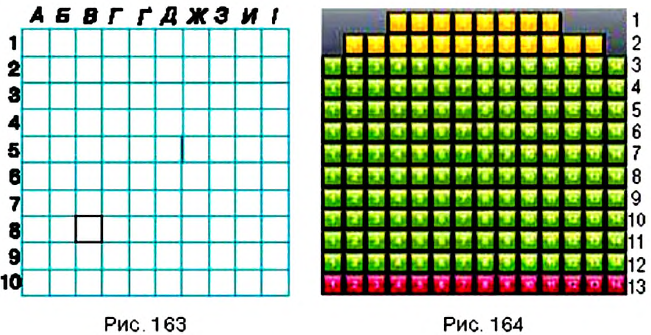
Вы знаете, что в игре «Морской бой» положение корабля определяют с помощью «координат» из цифр и «координат» из букв (рис. 163). В зависимости от выбранной буквы передвигаются на определённое количество клеточек вправо или влево, а цифра указывает, на сколько клеточек нужно сместиться вверх или вниз. Итак, место корабля на поле боя определяют двумя « координатами».
Чтобы определить место в зале кинотеатра, также нужно знать две «координаты»: номер ряда и номер кресла в этом ряду (рис. 164). Причём порядок «координат» в такой паре является строго определённым. Действительно, например, пары чисел 3 и 12 и 12 и 3 направят нас в совершенно разные места зала: в 3-й ряд на 12-е место или в 12-й ряд на 3-е место. В отличие от предыдущего примера, для ориентирования в зале кинотеатра порядок координат не меняют, поскольку неудобно сначала искать номер места в ряду, а лишь затем — сам ряд.
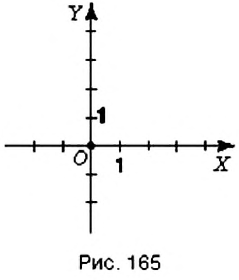
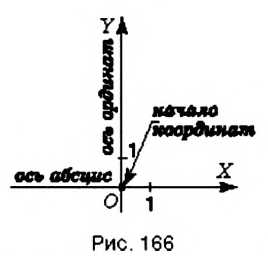
Итак, чтобы охарактеризовать размещение точки на плоскости, нужно задать две координатные прямые с равными единичными отрезками, одна из которых задаёт направление вправо-влево, а вторая — вверх-вниз. Для этого координатные прямые изображают перпендикулярно друг к другу и так, чтобы начала отсчёта на них совпадали (рис. 165). Одну из этих прямых (как правило, горизонтальную) считают первой, а другую — второй. Такая пара координатных прямых образует прямоугольную систему координат.
Первую координатную прямую называют осью абсцисс. Её обозначают 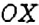
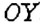
Плоскость с заданной на ней системой координат называют координатной плоскостью.
Каждой точке на плоскости можно поставить в соответствие пару чисел, взятых в определённом порядке, и наоборот, каждой паре чисел соответствует единственная точка координатной плоскости. Такая упорядоченная пара чисел называется координатами точки в данной системе координат. Координату по оси абсцисс называется абсциссой точки, а координату по оси ординат — ординатой точки.

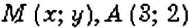
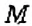
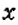
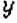
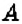
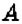
Пример:
На координатной плоскости постройте точку: 1) 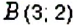
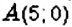
Решение:
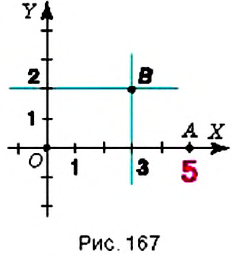
Введём прямоугольную систему координат на плоскости (рис. 167).
1. У точки 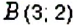
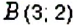
2. Поскольку ордината точки 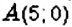
Обратите внимание:
- точка лежит на оси абсцисс, если её ордината равна нулю, и наоборот;
- точка лежит на оси ординат, если её абсцисса равна нулю, и наоборот;
- начало координат — точка
, имеет координаты
.
Пример:
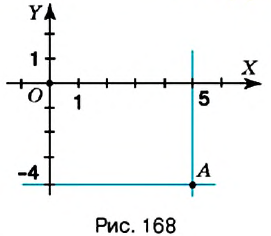
Как определить координаты точки, построенной на координатной плоскости, например, точки 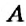
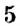
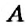
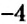
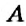
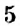
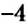
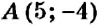
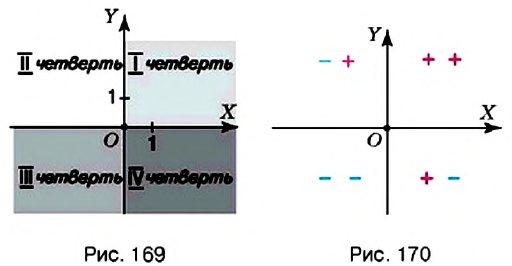
Координатные оси разбивают координатную плоскость на четыре части. Их называют координатными четвертями и обозначают так: I четверть, II четверть, III четверть, IV четверть (рис. 169).
Точки I четверти имеют положительную абсциссу и положительную ординату. И наоборот, если абсцисса и ордината точки положительные, то она лежит в I четверти, как, например, точка 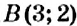
На рисунке 170 показаны знаки координат точек, лежащих в соответствующих четвертях.
Положение любой точки на поверхности Земли определяется двумя координатами: географической широтой и географической долготой.
Географические координаты ввёл древнегреческий учёный Гиппарх во И в. до н.э. Географические координаты применяют для определения положения точек земной поверхности относительно экватора и начального (нулевого) меридиана. Например, Киев имеет следующие географические координаты: 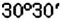
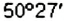
Графики зависимостей между величинами
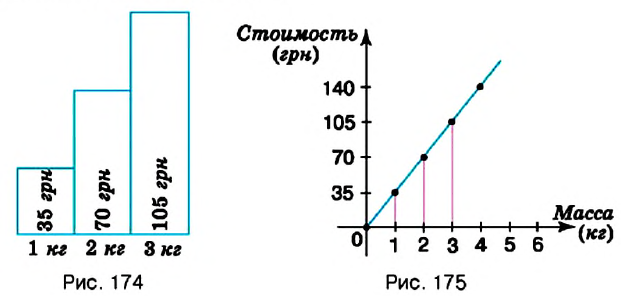
Вы знаете, что стоимость товара зависит от его количества: чем большее количество товара покупают, тем большей будет его стоимость. Например, если цена одного килограмма конфет составляет 35 грн, то за 2 кг нужно заплатить 70 грн, за 3 кг — 105 грн и т.п. Вы знаете, что такое соответствие можно наглядно отобразить на диаграмме (рис. 174). Однако по диаграмме трудно определить, сколько стоит 2,5 кг конфет или иное их количество. Изобразим данные о стоимости конфет не в виде столбиков, а вертикальными отрезками в системе координат (рис. 175). Поскольку величины «масса конфет» и «стоимость покупки» являются прямо пропорциональными, то верхние концы столбиков диаграммы можно соединить отрезками. Получим линию, показывающую, как изменяется стоимость покупки в зависимости от массы конфет. Такая линия называется графиком зависимости величины «стоимость покупки» от величины «масса конфет».
Обратите внимание:
все точки графика зависимости прямо пропорциональных величин лежат на одной прямой.
Вы знаете, что расстояние и время на его преодоление являются прямо пропорциональными величинами. Поэтому все точки графика движения лежат на одной прямой.
Пример:
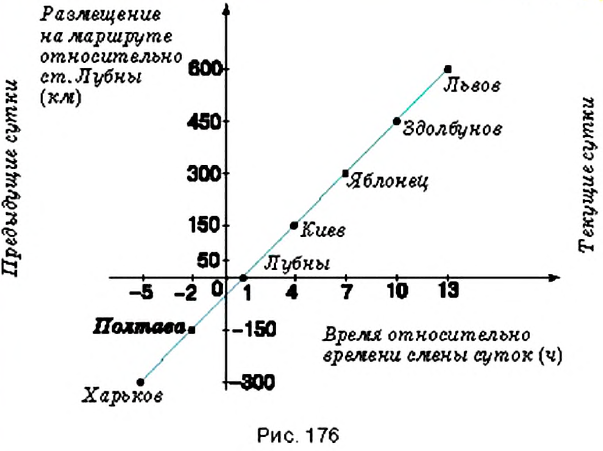
Поезд Харьков — Львов выходит из Харькова около 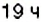
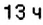
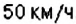
1) В котором часу новых суток поезд делает первую остановку? Какая это станция?
2) Что показывает число 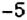
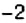
3) На каких расстояниях от первой остановки поезд останавливается на других станциях?
4) Что показывает число 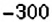
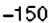
5) Каковы координаты конечных точек маршрута?
Решение:
По условию задачи, движение поезда начинается в 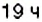
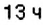
1. Начало новых суток поезд встречает недалеко от станции Лубны, а первую остановку делает в 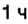
2. Поскольку движение поезда началось в предыдущие сутки, то по оси абсцисс время его отправления из Харькова можно выразить отрицательным числом 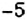
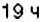
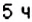
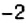
3. Остановки запланированы через каждые 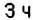
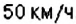
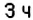
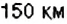
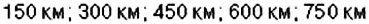
4. При помощи отрицательных чисел 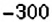
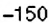
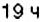
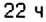
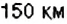
5. Конечные результаты точки маршрута поезда имеют координаты 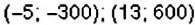
Пример:
Обязательно ли выбирать конечные точки маршрута для построения графика движения? Нет. График можно построить по любым двум его точкам. Но концы маршрута нужно отметить обязательно.
Обратите внимание:
график движения является прямой (или её частью), поэтому такой график можно построить по любым двум его точкам.
С помощью графиков можно решать целый класс задач. Рассмотрим задачу.
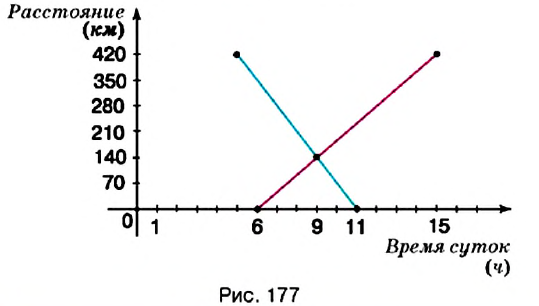
Пример:
Из пунктов 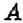
Решение:
Построим в прямоугольной системе координат графики движения автомобилей (рис. 177). Красный отрезок — график движения красного автомобиля, синий — синего автомобиля. Точке пересечения этих отрезков соответствует время — 9 ч. Итак, автомобили встречаются в 9 ч.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Линейное уравнение с одной переменной
- Целые выражения
- Одночлены
- Многочлены
- Обыкновенные дроби
- Отношения и пропорции
- Рациональные числа и действия над ними
- Делимость натуральных чисел
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Как решать квадратные уравнения без дискриминантаСкачать

Алгоритм расчёта вещественных корней полиномов
Основополагающая идея этого алгоритма очень проста и может быть изложена двумя предложениями. Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома. Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.
А теперь по порядку.
Проблема нахождения корней алгебраических полиномов известна давно, по крайней мере со средневековья. В школе учат решать квадратные уравнения. В википедии можно найти формулы Кардано для решения кубических уравнений и описание метода Феррари для решения в радикалах уравнения четвёртой степени. Там же описан метод Лобачевского для решения алгебраических уравнений произвольной степени. Суть метода Лобачевского вкратце сводится к следующему.
Нетрудно, имея некоторый исходный полином, построить полином2, имеющий те же по модулю корни, что и исходный полином, но с противоположным знаком. Перемножая исходный полином и полином2, получаем полином, корни которого равны квадратам корней исходного полинома.
Это преобразование (квадрирование) полезно повторить несколько раз. В результате, если корни исходного полинома не были равны друг другу, их многократно квадрированные значения оказываются далеко разнесёнными по величине, а их приближенные значения очень просто выражаются через коэффициенты соответствующего квадрированного полинома.
В частности, если коэффициент при старшей степени аргумента полинома равен единице, то следующий по старшинству коэффициент равен (с обратным знаком) сумме корней уравнения, а поскольку значения этих корней сильно разнесены, то приближенно можно считать эту сумму равной наибольшему по модулю корню.
Для конкретности сообщим, что для полинома 4-й степени с корнями 1, 2, 3, 4 метод Лобачевского уже после четвёртого квадрирования даёт правильные до второго знака после запятой значения корней. При этом для представления коэффициентов полиномов достаточно формата long double.
Бесспорно, этот метод является ценным инструментом в руках исследователя, наделённого интеллектом. Однако, его программирование для современной вычислительной техники вызывает серьёзные затруднения при необходимости строгой гарантии достоверности результата при всевозможных особых случаях расположения корней.
Теперь я начну описывать иной метод. В общедоступной печати упоминание о нём начинается с работы [1]. Какие-либо независимые публикации о применении такого метода мне неизвестны. Этот алгоритм сводится к последовательному исследованию интервалов монотонного изменения исходного полинома. Если на границах этого интервала монотонности значения полинома имеют разные знаки, то запускается процедура деления отрезка пополам для расчёта точного значения очередного корня. Границами интервалов монотонности являются точки, в которых значение производной полинома обращается в нуль, т.е. это корни производного полинома. Производный полином имеет степень на единицу меньшую, чем исходный полином, и процесс расчёта коэффициентов производных полиномов следует продолжить до полинома первой степени, корень которого находится непосредственно, без привлечения процедуры деления отрезка пополам. В результате этого шага получим два интервала монотонного изменения для производного полинома второй степени.
Теперь можно найти два вещественных корня производного полинома второй степени (если они существуют) и далее по лестнице из производных полиномов подниматься до корней исходного полинома. Остаётся пояснить, как технически реализуются границы «плюс, минус бесконечность» интервалов монотонности исходного и производных полиномов.
Нормируем полином так, чтобы коэффициент при старшей степени аргумента стал равным единице. Пусть M — наибольшее по модулю значение среди его остальных коэффициентов. Тогда значение полинома больше единицы для всех значений аргумента, больших, чем M+1.
Для доказательства рассмотрим расчёт полинома p(x)=x^n+k[n-1]*x^(n-1)+. +k[1]*x+k[0] по схеме Горнера.
На первом шаге вычисляется p[1]=k[n-1]+x и очевидно, что p[1]>1.
На втором шаге вычисляется p[2]=k[n-2]+x*p[1] и вновь очевидно, что p[2]>1.
Аналогичное имеет место на последующих шагах.
На последнем шаге вычисляется p(x)=k[0]+x*p[n-1] и окончательно получим p(x)>1.
Таким образом, если нужно определить знак полинома при бесконечном значении аргумента, следует взять аргумент равным M+1.
Прилагаемый текст соответствующей программы вполне заменяет занудное изложение отдельных технических подробностей описанного тут алгоритма.
Прокомментирую, наконец, не вполне очевидную особенность реализации алгоритма деления отрезка пополам.
Пробная точка pt, расположенная посередине между текущими концами ng и vg отрезка, вычисляется оператором pt=0.5*(ng+vg); а цикл делений пополам прерывается оператором if(pt =vg)break;.
В силу конечной точности представления вещественных чисел в машине рано или поздно наступает состояние, при котором операция деления пополам вместо нового числа даёт значение одной из исходных границ. Именно в этом состоянии следует прекратить цикл делений пополам. Это состояние соответствует максимально достижимой точности результата.
Недавно мне удалось использовать этот алгоритм для решения задачи вычисления комплексного корня полинома, не имеющего вещественных корней. Но об этом я планирую рассказать на Хабре в следующей статье.
Ниже, как приложение, приведен полный текст файла polynomRealRoots.cpp, реализующего описанныйалгоритм.
Примите также текст заголовочного файла polynomRealRoots.h, позволяющего легко организовать ссылку на приведенный выше программный модуль.
Литература
1. Костин И.К. Семейство алгоритмов расчета интервалов прохождения космического аппарата над круговым наземным объектом с учетом продольной ошибки определения параметров орбиты
Вопросы радиоэлектроники, сер. РЛТ, 2004г., вып. 1
Эту ссылку можно найти в Яндексе поиском по закавыченной фразе «семейство алгоритмов расчета», но текст этой статьи в электронном виде, кажется, недоступен. Поэтому приведу здесь цитату из двух предложений этой статьи:
Вещественный корень полинома всегда находится на участке монотонного изменения полинома, т.е. между корнями производной полинома.
Но производная полинома — это тоже полином, однако, меньшей степени и, найдя его вещественные корни, надо искать корни исходного полинома между корнями производной методом деления пополам.
🎬 Видео
11 класс, 27 урок, Общие методы решения уравненийСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Решение биквадратных уравнений. 8 класс.Скачать

Как решают уравнения в России и СШАСкачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Одно уравнение и два метода решения #shortsСкачать

Математика | Решение уравненийСкачать

Как решают уравнения в России и США!?Скачать

Решение уравнений - математика 6 классСкачать

Как решать уравнения с дробью? #shortsСкачать

9 класс, 11 урок, Методы решения систем уравненийСкачать

Решение уравнений сводящихся к квадратным уравнениям. Биквадратные уравнения – 8 класс алгебраСкачать

Как решить уравнение #россия #сша #америка #уравненияСкачать

Квадратные уравнения от «А» до «Я». Классификация, решение и теорема Виета | МатематикаСкачать

Решение матричных уравненийСкачать

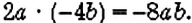
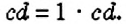
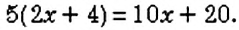
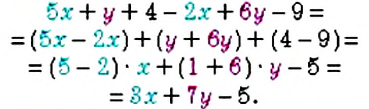
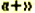 , то при раскрытии скобок знаки слагаемых в скобках сохраняют;
, то при раскрытии скобок знаки слагаемых в скобках сохраняют; , то при раскрытии скобок знаки слагаемых в скобках изменяют на противоположные.
, то при раскрытии скобок знаки слагаемых в скобках изменяют на противоположные.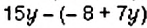
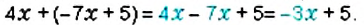
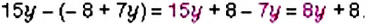
 и
и  используют для обозначения действий сложения и вычитания. Эти знаки ввёл чешский учёный И. Видман в 1489 г в книге «Быстрый и приятный счёт для всех торговцев»(рис. 138).
используют для обозначения действий сложения и вычитания. Эти знаки ввёл чешский учёный И. Видман в 1489 г в книге «Быстрый и приятный счёт для всех торговцев»(рис. 138).
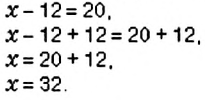
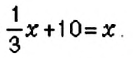
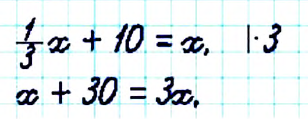
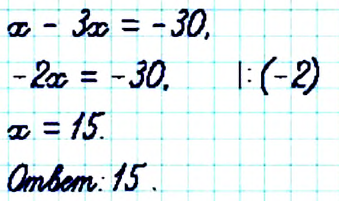




 , имеет координаты
, имеет координаты 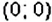 .
.