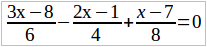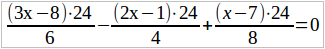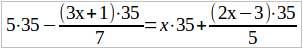Что такое свойства равенств 4 класс уравнения

Два числовых или буквенных выражения, соединённых знаком = (равно), составляют равенство. Выражение, стоящее слева от знака = , называется левой или первой частью равенства, а стоящее справа от него — правой или второй частью равенства:

Части равенства можно менять местами. Например, если

Равенства делятся на два типа: тождества и уравнения.

Свойства равенств

Все равенства имеют два свойства, на которых основано преобразование и решение уравнений:

1) Обе части равенства можно увеличить или уменьшить на одно и то же число или алгебраическое выражение – равенство от этого не нарушится.

2) Обе части равенства можно умножить или разделить на одно и то же число или алгебраическое выражение (не равное нулю) – равенство от этого не нарушится.

Математика

50. Свойства равенств, на которых основывается решение уравнений . Возьмем какое-нибудь уравнение, не очень сложное, например:

x/2 – (x – 3)/3 – (x – 5)/6 = 1

Мы видим в каждом уравнении знак равенства: все то, что написано слева от знака равенства, называется левою или первою частью уравнения (в первом уравнении 7x – 24 является левою или первою частью, а во втором x/2 – (x – 3)/3 – (x – 5)/6 есть первая, или левая, часть); все то, что написано справа от знака равенства, называется правою или второю частью уравнения (15 – 3x есть правая часть первого уравнения, 1 является правою, или вторю, частью 2-го уравнения).

Каждая часть любого уравнения выражает собою некоторое число. Числа, выражаемые левою и правою частью уравнения, должны быть равны между собою. Нам ясно: если мы к каждому из этих чисел прибавим по одинаковому числу, либо вычтем из них по одинаковому числу, либо каждое из них умножим на одинаковое число, либо, наконец, разделим на одно и то же число, то результаты этих действий должны также быть равными между собою. Другими словами: если a = b, то a + c = b + c, a – c = b – c, ac = bc и a/c = b/c. По поводу деления следует, однако, иметь в виду, что в арифметике не имеется деления на нуль — мы не умеем, например, число 5 разделить на нуль. Поэтому в равенстве a/c = b/c число c не может быть равным нулю.

1. К обеим частям уравнения можно прибавить или из них вычесть по одинаковому числу.
2. Обе части уравнения можно умножить или разделить на одно и то же число, исключая случай, когда это число может оказаться равным нулю.

Пользуясь этими свойствами уравнения, мы можем найти удобный способ решать уравнения. Выясним этот случай на примерах.

Пример 1. Пусть надо решить уравнение

Мы видим, что первая часть уравнения содержит два члена; один из них 5x, содержащий неизвестный множитель x, можно назвать неизвестным членом, а другой –7 – известным. Во второй части уравнения также 2 члена: неизвестный 4x и известный +15. Сделаем так, чтобы в левой части уравнения оказались только неизвестные члены (а известный член –7 уничтожился бы), а в правой части оказались бы только известные члены (а неизвестный член +4x уничтожился бы). Для этой цели прибавим к обеим частям уравнения одинаковые числа: 1) прибавим по +7 (чтобы уничтожился член –7) и 2) прибавим по –4x (чтобы уничтожился член +4x). Тогда получим:

5x – 7 + 7 – 4x = 4x + 15 + 7 – 4x

Сделав в каждой части уравнения приведение подобных членов, получим

Это равенство и является решением уравнения, так как оно указывает, что для x надо взять число 22.

Пример 2. Решить уравнение:

Опять прибавим к обеим частям уравнения по –11 и по +4x, получим:

8x + 11 – 11 + 4x = 7 – 4x – 11 + 4x

Выполнив приведение подобных членов, получим:

Разделим теперь обе части уравнения на +12, получим:

x = –4/12 или x = –1/3

(первую часть уравнения 12x разделить на 12 – получим 12x/12 или просто x; вторую часть уравнения –4 разделить на +12 – получим –4/12 или –1/3).

Последнее равенство и является решением уравнения, так как оно указывает, что для x надо взять число –1/3.

Пример 3. Решить уравнением

x – 23 = 3 · (2x – 3)

Раскроем сначала скобки, получим:
x – 23 = 6x – 9

Прибавим к обеим частям уравнения по +23 и по –6x, – получим:

x – 23 + 23 – 6x = 6x – 9 + 23 – 6x.

Теперь, для того, чтобы впоследствии ускорить процесс решения уравнения, не будем сразу выполнять приведение всех подобных членов, а только заметим, что члены –23 и +23 в левой части уравнения взаимно уничтожаются, также члены +6x и –6x в первой части взаимно уничтожаются – получим:

Сравним это уравнение с начальным: вначале было уравнение:

Теперь получили уравнение:

Мы видим, что в конце концов оказалось, что член –23, находившийся сначала в левой части уравнения, теперь как бы перешел в правую часть уравнения, причем у него переменился знак (в левой части начального уравнения был член –23, теперь его там нет, но зато в правой части уравнения имеется член + 23, которого там раньше не было). Так же точно в правой части уравнения был член +6x, теперь его там нет, но появился зато в левой части уравнения член –6x, которого раньше там не было. Рассматривая с этой точки зрения примеры 1 и 2, мы придем к общему заключению:

Можно любой член уравнения перенести из одной части в другую, меняя знак у этого члена (в дальнейших примерах мы будем этим пользоваться).

Итак, возвращаясь к нашему примеру, мы получили уравнение

Выполним приведение подобных членов:

Разделим обе части уравнения на –5. Тогда получим:

[–5x : (–5) получим x] – это и есть решение нашего уравнения.

Пример 4. Решить уравнение:

Сделаем так, чтобы в уравнении не было дробей. Для этой цели найдем общего знаменателя для наших дробей – общим знаменателем служит число 24 – и умножим на него обе части нашего уравнения (можно, ведь, чтобы равенство не нарушалось, умножить на одно и то же число только обе части уравнения). В первой части 3 члена, причем каждый член является дробью — надо, следовательно, каждую дробь умножить на 24: вторая часть уравнения есть 0, а нуль умножить на 24 — получим нуль. Итак,

Мы видим, что каждая из наших трех дробей, благодаря тому, что она умножена на общее наименьшее кратное знаменателей этих дробей, сократится и сделается целым выражением, а именно получим:

(3x – 8) · 4 – (2x – 1) · 6 + (x – 7) · 3 = 0

Конечно, желательно все это выполнить в уме: надо вообразить, что, например, числитель первой дроби заключается в скобки и умножается на 24, после чего воображение поможет нам увидеть сокращение это дроби (на 6) и конечный результат, т. е. (3x – 8) · 4. Тоже имеет место и для остальных дробей. Раскроем теперь в полученном уравнении (в его левой части) скобки:

12x – 32 – 12x + 6 + 3x – 21 = 0

(обратим внимание, что здесь понадобилось двучлен 2x – 1 умножить на 6 и полученное произведение 12x – 6 вычесть из предыдущего, благодаря чему знаки членов этого произведения должны перемениться — выше и написано –12x + 6). Перенесем известные члены (т. е. –32, +6 и –21) из левой части уравнения в его правую часть, причем (как мы уже знаем) знаки этих членов должны перемениться — получим:

12x – 12x + 3x = 32 – 6 + 21.

Выполним приведение подобных членов:

(при навыке должно сразу выполняться и перенесение нужных членов из одной части уравнения в другую и приведение подобных членов), разделим, наконец, обе части уравнения на 3 — получим:

x = 15(2/3) — это и есть решение уравнения.

Пример 5. Решить уравнение:

5 – (3x + 1)/7 = x + (2x – 3)/5

Здесь две дроби, и их общий знаменатель равен 35. Умножим, чтобы освободить уравнение от дробей, обе части уравнения на общего знаменателя 35. В каждой части нашего уравнения 2 члена. При умножении каждой части на 35 должно каждый член умножить на 35 — получим:

Дроби сократятся — получим:

175 – (3x + 1) · 5 = 35x + (2x – 3) · 7

(конечно, можно было бы при навыке написать сразу это уравнение).

Выполним все действия:

175 – 15x – 5 = 35x + 14x – 21.

Перенесем все неизвестные члены из правой части (т. е. члены +35x и +14x) в левую, а все известные члены из левой части (т. е. члены +175 и –5) в правую — следует при этом не забывать у переносимых членов менять знак:

–15x – 35x – 14x = –21 – 175 + 5

(член –15x, как раньше был в левой части, так и теперь в ней остался — у него поэтому отнюдь не следует менять знака; аналогичное имеет место и для члена –21). Сделав приведение подобных членов, получим:

[Возможно сделать так, чтобы не было знака минус в обеих частях уравнения; для этого умножим обе части уравнения на (–1), получим 64x = 191, но этого можно и не делать.]
Разделим затем обе части уравнения на (–64), получим решение нашего уравнения

[Если умножили обе части уравнения на (–1) и получили уравнение 64x = 191, то теперь надо обе части уравнения разделить на 64.]

На основании того, что пришлось выполнять в примерах 4 и 5, мы можем установить: можно освободить уравнение от дробей — для этого надо найти общего знаменателя для всех дробей, входящих в уравнение (или наименьшее общее кратное знаменателей всех дробей) и на него умножить обе части уравнения — тогда дроби должны исчезнуть.

Пример 6. Решить уравнение:

Перенеся член 4x из правой части уравнения в левую, получим:

5x – 4x = 0 или x = 0.

Итак, решение найдено: для x надо взять число нуль. Если мы заменим в данном уравнении x нулем, получим 5 · 0 = 4 · 0 или 0 = 0, что указывает на выполнение требования, выражаемого данным уравнением: найти такое число для x, чтобы одночлен 5x оказался равен тому же самому числу, как и одночлен 4x.

Если кто-либо подметит с самого начала, что обе части уравнения 5x = 4x можно разделить на x и выполнит это деление, то получится явная несообразность 5 = 4! Причиною этого является то обстоятельство, что деление 5x/x в данном случае выполнить нельзя, так как, мы видели выше, вопрос, выражаемый нашим уравнением, требует, чтобы x = 0, а деление на нуль не выполнимо.

Заметим еще, что и умножение на нуль требует некоторой внимательности: умножая на нуль и два неравных числа, мы получим в результате этих умножений равные произведения, а именно — нули.

Если, например, мы имеем уравнение

x – 3 = 7 – x (его решение: x = 5)

и если кто-либо захочет к нему применить свойство «обе части уравнения можно умножить на одно и тоже число» и умножить обе части на x, то получит:

x 2 – 3x = 7x – x 2 .

После этого может обратить на себя внимание, что все члены уравнения содержат множителя x, из чего можно сделать заключение, что для решения этого уравнения можно взять число нуль, т. е. положить x = 0. И в самом деле, тогда получим:
0 2 – 3 · 0 = 7 · 0 – 0 2 или 0 = 0.

Однако, это решение x = 0, очевидно, не годится для данного уравнения x – 3 = 7 – x; заменяя в нем x нулем, получим явную несообразность: 3 = 7!

Урок математики в 4-м классе по теме «Первое свойство равенства». Система РО Л.В. Занкова

Основание: развитие ума, воли, чувств.

Идея: самостоятельный выход на свойство равенств.

1. Установление закономерности.
2. На основе закономерности формулирование правила.
3. Формирование умения оценивать действия по критериям: правильность; осознанность.

Тип урока: объяснение нового материала.

Оборудование: таблица a = b; a + c = b + c; a – c = b – c.

Этапы урока

Цель этапа

Содержание урока

Способ взаимодействия1. Организационный момент.Проверка готовности к уроку.Слово учителя.Фронтальная работа.2. Подготовительная работа к усвоению нового.

Математический диктант.Выход на тему урока.

Самооценка.1. Запишите результаты устных вычислений в строчку:

• разность чисел 500 и 20 уменьшить в 8 раз;
• произведение 30 и 10 уменьшить в 50 раз.
• частное 300 и 50 увеличить на 14;
• произведение 90 и 4 уменьшить на 60;
• частное 640 и 8 уменьшить в 10 раз;
• 140 уменьшить на 50 и увеличить в 3 раза;
• 280 разделить на 40 и увеличить на 23;
• разность 540 и 40 уменьшить в 5 раз;
• произведение 5 и 90 увеличить на 3 десятка;
• 200 уменьшить на 140 и уменьшить в 20 раз.

2. Проверка выполнения по ответам на доске:

60,5, 20, 300, 8,270, 30,100, 480, 3.

3. Оцените свою работу.

— По какому критерию оценивали? (За правильность вычислений.)

4. Придумать задания к этим числам.

(Найти числа, связанные между собой и записать с ними равенства.)

5. Проверка выполнения.

— Прочитайте, какие равенства у вас получились.

300 – 30 =270

Обсуждение в парах.3. Изучение нового.-Увеличьте части равенства на одно и то же число и найдите значения выражений.

-Что заметили? (Значение равенства не изменилось.)

-Уменьшите части равенства на одно и то же число.

— Проверьте закономерность на равенстве:

— Что заметили? (Не получилось равенство.)

— Почему не получилось верное равенство? (Потому, что неверно вычислили, должно быть 104, а не 14. Это была «ловушка».)4. Обобщение.Сравнение своего понимания с другим «Я».— Сделайте вывод по вашим наблюдениям.

— Сравните свой вывод с правилом в учебнике (стр.71).

— Назовите тему урока. (Свойства равенств.)5. Закрепление.— Как записать это свойство в общем виде?

(а = в, то а + с = в + с и а – с = в – с)

— Что обозначают буквы а, в, с?

— Для чего нужно это свойство? (Чтобы осознанно решать.)

— Что значит «осознанно»?

— Проверим, как работает это свойство равенства в сложных выражениях.

— Обсудите в парах, как, используя знаки действий, получить верные равенства.

— Обе части каждого равенства сначала увеличь, а потом уменьши на одно и то же число.

— Какую заметили закономерность?

— Зачем выполняли это задание? (Чтобы понять закономерность.)

— Можно ли сказать, что мы работали осознанно?

— Значит, теперь мы можем оценивать себя по новому критерию-осознанности.

Работа в парах.6. Итог урока.Рефлексия.— Все ли задания выполняли правильно?

— Что должны делать, чтобы работать осознанно? (Знать правила, закономерности.)

📽️ Видео