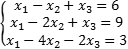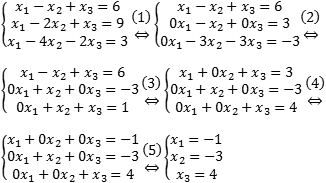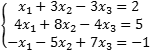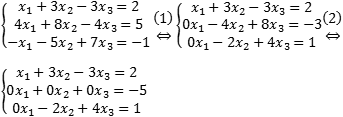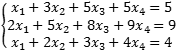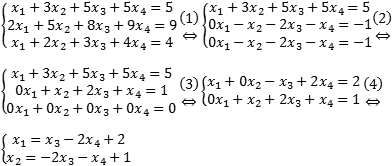Что такое противоречивая система уравнений (8 видео)

Содержание

Как вы знаете, когда система уравнений противоречива? — Алгебра — 2022
Метод Гаусса
04. Метод Гаусса
📽️ Видео

Видео:Решение систем уравнений методом подстановкиСкачать

Как вы знаете, когда система уравнений противоречива? — Алгебра — 2022

Когда вы пытаетесь решить систему, вы получаете невозможное.
Вы получаете что-то вроде #3=8# или же # х + 5 = х-2 # (что привело бы к #5=-2#

Если вы работаете с действительными числами с нелинейными системами, вы можете вместо этого получить воображаемое решение.

(Например: # У = х ^ 2 + 5 # а также # У = х + 1 # , По замене: # Х ^ 2-х + 4 = 0 # но # Б ^ 2-4ac = (- 1) ^ 2-4 (1) (4)) # отрицательно.)

Система несовместна, если решение одного уравнения является несовместимо с являясь решением другого уравнения в системе.

Быть «несовместимым» означает, что они не могут произойти.
Например: быть отрицательным несовместимо с быть позитивным
Быть меньше 4 непоследовательный с быть больше, чем 9.

Быть решением для # У = 3x + 1 # несовместимо с тем, чтобы быть решением # У = 3x-6 # .
( # У # быть более чем # 3x # несовместимо с # У # будучи на 6 меньше, чем # 3x #

Система:
# У = 3x + 1 #
# У = 3x-6 # .
противоречиво

Видео:Система уравнений. Метод алгебраического сложенияСкачать

Метод Гаусса

Две системы линейных уравнений называются , если множество всех их решений совпадает.

системы уравнений — это:

Вычеркивание из системы тривиальных уравнений, т.е. таких, у которых все коэффициенты равны нулю;
Умножение любого уравнения на число, отличное от нуля;
Прибавление к любому i -му уравнению любого j -то уравнения, умноженного на любое число.

Переменная x_i называется , если эта переменная не является разрешенной, а вся система уравнений — является разрешенной.

Теорема. Элементарные преобразования переводят систему уравнений в равносильную.

Смысл метода Гаусса заключается в том, чтобы преобразовать исходную систему уравнений и получить равносильную разрешенную или равносильную несовместную систему.

Итак, метод Гаусса состоит из следующих шагов:

Рассмотрим первое уравнение. Выберем первый ненулевой коэффициент и разделим все уравнение на него. Получим уравнение, в которое некоторая переменная x_i входит с коэффициентом 1;
Вычтем это уравнение из всех остальных, умножая его на такие числа, чтобы коэффициенты при переменной x_i в остальных уравнениях обнулились. Получим систему, разрешенную относительно переменной x_i , и равносильную исходной;
Если возникают тривиальные уравнения (редко, но бывает; например, 0 = 0), вычеркиваем их из системы. В результате уравнений становится на одно меньше;
Повторяем предыдущие шаги не более n раз, где n — число уравнений в системе. Каждый раз выбираем для «обработки» новую переменную. Если возникают противоречивые уравнения (например, 0 = 8), система несовместна.

В результате через несколько шагов получим либо разрешенную систему (возможно, со свободными переменными), либо несовместную. Разрешенные системы распадаются на два случая:

Число переменных равно числу уравнений. Значит, система определена;
Число переменных больше числа уравнений. Собираем все свободные переменные справа — получаем формулы для разрешенных переменных. Эти формулы так и записываются в ответ.

Вот и все! Система линейных уравнений решена! Это довольно простой алгоритм, и для его освоения вам не обязательно обращаться к репетитору высшей по математике. Рассмотрим пример:

Задача. Решить систему уравнений:

Вычитаем первое уравнение из второго и третьего — получим разрешенную переменную x ₁;
Умножаем второе уравнение на (−1), а третье уравнение делим на (−3) — получим два уравнения, в которых переменная x ₂ входит с коэффициентом 1;
Прибавляем второе уравнение к первому, а из третьего — вычитаем. Получим разрешенную переменную x ₂;
Наконец, вычитаем третье уравнение из первого — получаем разрешенную переменную x ₃;
Получили разрешенную систему, записываем ответ.

совместной системы линейных уравнений — это новая система, равносильная исходной, в которой все разрешенные переменные выражены через свободные.

Когда может понадобиться общее решение? Если приходится делать меньше шагов, чем k ( k — это сколько всего уравнений). Однако причин, по которым процесс заканчивается на некотором шаге l k , может быть две:

После l -го шага получилась система, которая не содержит уравнения с номером ( l + 1). На самом деле это хорошо, т.к. разрешенная система все равно получена — даже на несколько шагов раньше.
После l -го шага получили уравнение, в котором все коэффициенты при переменных равны нулю, а свободный коэффициент отличен от нуля. Это противоречивое уравнение, а, следовательно, система несовместна.

Важно понимать, что возникновение противоречивого уравнения по методу Гаусса — это достаточное основание несовместности. При этом заметим, что в результате l -го шага не может остаться тривиальных уравнений — все они вычеркиваются прямо в процессе.

Задача. Исследовать совместность и найти общее решение системы:

Вычитаем первое уравнение, умноженное на 4, из второго. А также прибавляем первое уравнение к третьему — получим разрешенную переменную x ₁;
Вычитаем третье уравнение, умноженное на 2, из второго — получим противоречивое уравнение 0 = −5.

Итак, система несовместна, поскольку обнаружено противоречивое уравнение.

Задача. Исследовать совместность и найти общее решение системы:

Вычитаем первое уравнение из второго (предварительно умножив на два) и третьего — получим разрешенную переменную x ₁;
Вычитаем второе уравнение из третьего. Поскольку все коэффициенты в этих уравнениях совпадают, третье уравнение превратится в тривиальное. Заодно умножим второе уравнение на (−1);
Вычитаем из первого уравнения второе — получим разрешенную переменную x ₂. Вся система уравнений теперь тоже разрешенная;
Поскольку переменные x ₃ и x ₄ — свободные, переносим их вправо, чтобы выразить разрешенные переменные. Это и есть ответ.

Итак, система совместная и неопределенная, поскольку есть две разрешенных переменных ( x ₁ и x ₂) и две свободных ( x ₃ и x ₄).

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

04. Метод Гаусса

СИстеме линейных уравнений (1) соответствуют три матриц

, .

Первая матрица называется Матрицей системы, вторая — Расширенной или Присойдиненной матрицей системы, третья — Столбцом свободных членов.

Система линейных уравнений называется Системой ступенчатого вида, если расширенная матрица системы есть матрица ступенчатого вида. Неизвестные с коэффициентами неравными нулю, которые стоят первыми в уравнениях системы ступенчатого вида называются Главными неизвестными, а остальные неизвестные называются Свободными.

Линейное уравнение, в котором все коэффициенты равны нулю, а свободный член не равен нулю, т. е. уравнение вида:

Не имеет решений. Действительно, если — решение этого уравнения, то получим противоречие с условием. Такое уравнение называем Противоречивым.

Пусть не все уравнения системы (1) нулевые. Тогда и расширенная матрица системы (1) ненулевая. По теореме 2 ее можно конечным числом элементарных преобразований и преобразований выбрасывания нулевой строки можно привести к матрице ступенчатого вида. Полученной матрице соответствует система линейных уравнений ступенчатого вида. Этим преобразованиям расширенной матрицы системы (1) соответствуют такие же преобразования системы линейных уравнений (1). По теореме 1 они переводят систему (1) в равносильную систему линейных уравнений, которая будет являются системой ступенчатого вида.

Таким образом мы доказали первую часть следующей теоремы.

Теорема 3. Любую систему линейных уравнений, содержащую ненулевое уравнение конечным числом элементарных преобразований и преобразований вычеркивания нулевого уравнения можно привести к равносильной ей системе ступенчатого вида. При этом возможны следующие три случая.

1. Если в полученной системе линейных уравнений ступенчатого вида есть противоречивое уравнение, то данная система не имеет решений.

2. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе равно числу неизвестных, то данная система имеет единственное решение.

3. Если в полученной системе линейных уравнений ступенчатого вида нет противоречивого уравнения и число уравнений в полученной системе меньше числа неизвестных, то данная система имеет бесконечно много решение.

Доказательство. Пусть дана система (1), содержащая ненулевое уравнение. По выше доказанному, она конечным числом элементарных преобразований она может быть преобразована к равносильной ей системе уравнений ступенчатого вида. Возможны случаи.

В полученной системе ступенчатого вида есть противоречивое уравнение. Тогда ни один набор чисел Не удовлетворяет системе, и система (1) не имеет решений.

В полученной системе ступенчатого вида нет противоречивого уравнения. Тогда в каждом из уравнений системы ступенчатого вида содержится главное неизвестное. Отсюда получаем, что число главных неизвестных, а тем более число всех неизвестных, не менее числа уравнений в системе ступенчатого вида. Тогда возможны под случаи:

В системе ступенчатого вида число уравнений равно числу неизвестных, т. е. система имеет вид:

(12)

Где Все неизвестные в системе являются главными. Из последнего уравнения находим единственное значение для неизвестного : . Подставляя найденное значение в предпоследнее уравнение, находим для неизвестного единственное значение и т. д. Наконец из первого уравнения по найденным значениям неизвестных из первого уравнения находим единственное значение неизвестного . Таким образом, система (12), а поэтому и система (1) имеет единственное решение.

В системе ступенчатого вида число уравнений меньше числа неизвестных. В этом случае матрица полученной системы имеет вид (11), а

Систему можно записать в виде:

(13)

Где В этой системе R главных неизвестных , все остальные Свободные (в системе они обзначены точками. Возьмем для свободных неизвестных произвольные значения. Тогда значения главных неизвестных найдутся однозначно из системы (13). Так как главные неизвестные можно выбрать бесконечным числом способов, то получим, что система (13), а поэтому и система (1) имеет бесконечно много решений.

Следствие. Если в системе однородных уравнений число неизвестных больше числа уравнений, то система имеет бесконечно много решений.

Действительно, система однородных уравнений всегда имеет нулевое решение , и при приведении ее к ступенчатому виду всегда получим систему, в которой число неизвестных больше числа уравнений.

Метод исследования и решения систем линейных уравнений, изложенный в доказательстве теорем 3 называется методом Гаусса.

Пример 1. Решить систему

Составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Составим по полученной матрице ступенчатого вида систему линейных уравнений ступенчатого вида:

В полученной системе число уравнений равно числу неизвестных и полученная система имеет единственное решение, которое двигаясь вверх последовательно находим: