Что такое перекрестное правило в уравнениях

Видео:Как решать уравнения с дробью? #shortsСкачать

Love Soft

Инструменты пользователя

Инструменты сайта

Боковая панель

Навигация

Загрузки всякие

Связь

Содержание

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Отношение. Пропорция

Этап подготовки учащихся к сознательному усвоению нового материала

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Отношение

Отношение — частное двух чисел. Отношение показывает во сколько раз одно число больше другого или какую часть составляет одно число от другого.

Слова отношение и частное — математические синонимы. Разница в том, что члены отношения не могут быть нулями. Частное — термин из математики, отношение — слово из обычной жизни.

$$ 90 : 60 = frac = frac = 1,5$$

Первый способ записи более компактный, особенно он удобен, когда нужно записать отношение двух дробей: $$ frac <frac> <frac> = frac : frac $$

Многоэтажные дроби — отношения между дробями.

Два вида сравнения величин — абсолютное приращение и относительное — на сколько, во сколько.

Если две величины измерены одной и той же единицей измерения, то отношением этих величин называется отношение их числовых значений.

Основное свойство отношения:

отношение не изменится, если каждый из членов отношения умножить или разделить на одно и то же, отличное от 0, число.

Практические примеры

Видео:Как решают уравнения в России и США!?Скачать

Пропорция

Пропорция — равенство двух отношений.

Читается так: «отношение a к b равно отношению c к d» или — «a, деленное на b, равно c, деленному на d» или — «a относится к b, как c относится к d»

a и d называются крайними членами. c и d называются средними членами пропорции.

Основное свойство пропорции:

В верной пропорции произведение крайних членов равно произведению средних членов (перекрестное правило).

Гармония (от греч — связь, стройность) — соразмерность отдельных частей, слияние объектов в единое целое. В математике слово соразмерность определяется таким понятием как пропорция.

Правило

Если члены какой-нибудь пропорции поместить в квадрат, то любое отношение чисел, стоящих по одной стороны квадрата, равно отношению стоящих против них чисел по другой стороне. $$40 qquad 50 \ 16 qquad 20$$ Таким образом, получается ряд пропорций из одних и тех же чисел: $$ frac = frac qquad frac = frac \ frac = frac qquad frac = frac \ frac = frac qquad frac = frac \ frac = frac qquad frac = frac $$

Упражнение. Составьте всевозможные пропорции из чисел 4, 12, 10 и 30.

Упражнение. Составьте пропорции, у которых средними членами были бы 1) 6 и 9; 2) 15 и 7; 3) 0,5 и 1,1. Сколько решений имеет каждая из этих задач?

Тройное Правило. Даны три числа, чтобы найти четвёртое, умножают второе на третье и делят на первое.

Задача на пропорциональные части

Чтобы приготовить тесто для блинчиков, надо взять 8 мерок муки, 5 таких же мерок молока и 1 мерку масла.

Говорят, что продукты нужно взять в частях пропорционально числам 8, 5 и 1.

Сколько г муки надо взять, чтобы получилось 840 г теста.

Видео:Система уравнений. Метод алгебраического сложенияСкачать

Парадокс Арно

Данная пропорция носит название «парадокс Арно». Подумай, что в ней сомнительного?

Давай рассуждать вместе «1» больше, чем «−1» верно? Таким образом, согласно логике, левая часть пропорции должна быть больше, чем правая, но они равны… Вот он и парадокс

Видео:МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Где используется пропорция

Видео:ОГЭ по математике. Решаем уравнения | МатематикаСкачать

Прямая пропорциональность

Зависимость двух величин наз. прямой пропорциональностью, если при увеличении (уменьшении) одной величины в несколько раз во столько же раз увеличивается (уменьшается) другая величина. Если две величины являются прямо пропорциональными, то отношение значений одной величины равно отношению соответствующих значений другой величины.

Пример. 3 м ткани стоят 60 рублей, 6 м ткани стоят 120 рублей и т.д.

Коэффициент пропорциональности

Неизменное отношение пропорциональных величин называется коэффициентом пропорциональности. Коэффициент пропорциональности показывает, сколько единиц одной величины приходится на единицу другой. Обычно обозначают буквой k. Связь между пропорциональными величинами можно записать так: x = k * y.

Контрпример: площадь квадрата не пропорциональна длине его стороны.

Обратно пропорциональные величины — скорость и время. Пропорциональные и прямо пропорциональные величины — одно и тоже понятие. Слово «прямо» используется, чтобы подчеркнуть, что бывают другие виды пропорциональности.

Вопрос. Одна величина пропорциональна другой. Пропорциональна ли вторая величина первой? Приведите пример.

Задача

Пропорциональны ли величины, указанные в таблице?

Задача

Подбери четвертое слово так, чтобы оно «относилось» к третьему, как второе к первому:

Труд — награда, лень — …

Дружба — любовь, вражда — …

Кино — экран, театр — …

Человек — туловище, дерево — …

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Тройная пропорция

$$20 : 10 : 3 = 60 : 30 : 9$$

Тройную пропорцию можно разбить на три обычные пропорции:

$$20 : 10 = 60 : 30$$ $$10 : 3 = 30 : 9$$ $$20 : 3 = 60 : 9$$

Периметр треугольника равен 48 см, а длины его сторон относятся как 7:9:8. Найдите стороны треугольника.

Подсказка 1: Периметр треугольника — это сумма всех сторон треугольника.

Подсказка 2: Запиши тройную пропорцию и разбей ее на три обычные пропорции.

Подсказка 3: Обозначь одну сторону треугольника через x, а остальные стороны найди из пропорций.

Подсказка 4: Запиши выражение для периметра и приравняй 48.

Подсказка 5: Реши полученное уравнение.

Видео:Решить уравнение с дробями - Математика - 6 классСкачать

Пропорциональное деление на несколько частей

Пусть требуется число 414 разделить на 4 части пропорционально числам 7, 3, 4 и 9. Обозначим неизвестные части через $x_1, x_2, x_3, x_4$, зависимость записывается так: $$x_1 : x_2 : x_3 : x_4 = 7 : 3 : 4 : 9$$

Надо, чтобы в $x_1$ содержалось 7 некоторых долей, в $x_2$ — 3 доли, в $x_3$ — 4 доли и в $x_4$ — 9 таких же долей. Тогда во всем числе будет $7 + 3 + 4 + 9 = 23$ таких доли, одна доля окажется равной $414:23 = 18$, вслед за чем можно найти все неизвестные части.

Если числа, пропорционально которым надо разделить данное число, дробные, то их можно заменить пропорциональными им целыми. Так, если надо, чтобы

$$x_1 : x_2 : x_3 : x_4 = frac23 : 1frac12 : frac34 : 4$$,

множим все данные числа на 12:

$$x_1 : x_2 : x_3 : x_4 = 8: 18: 9 : 36$$

Отношения между числами от этого не изменятся, а все числа станут целыми.

Задача

Для приготовления фарфора берут 25 частей белой глины, 2 части песка и 1 часть гипса. Сколько каждого из этих материалов в чашке, весящей 92 г?

Задача

Разверстайте оплату счета за воду: 6 руб 40 коп — между семействами из 4, 7, 5, 3 и 4 человека.

Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Обьясните простыми словами «Перекрёстное правило»?

Математика | 5 — 9 классы

Обьясните простыми словами «Перекрёстное правило».

Если у двух равных пропорционально дробей( например 1 / 2 и 2 / 4) если умножить числитель первой дроби и знаменатель второй, то это произведение будет равно произведению числитель второй дроби на знаменатель первой.

а теперь применяем правило креста

х * 25, 2 = 6, 3 * 1

Видео:Решение уравнений, 6 классСкачать

Сформулируйте правило?

Разложение на простые множители это представление.

Видео:Как решают уравнения в России и СШАСкачать

Что такое взаимно простые числа?

Что такое взаимно простые числа?

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Признак делимости на четыре просто напишите правило или алгоритм?

Признак делимости на четыре просто напишите правило или алгоритм.

Видео:Уравнение. 5 класс.Скачать

Правила простой дроби?

Правила простой дроби.

Видео:Решение уравнений - математика 6 классСкачать

Обьясните мне пожалуйста, что такое метод подбора в данной задаче, тут наверное не так все просто?

Обьясните мне пожалуйста, что такое метод подбора в данной задаче, тут наверное не так все просто.

Видео:Решение уравнений. Как переносить слагаемые из одной части уравнения в другую. Математика 6 классСкачать

1 / 8 от 960 = ?

Обьясните пожалуйста такие примеры, я просто не понимаю.

Что нужно делать, что — бы найти ответ?

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Как обьяснить слово смежные ?

Как обьяснить слово смежные .

Видео:Решение систем уравнений методом подстановкиСкачать

Как сократить дробь?

Как сократить дробь?

Напишите пож))) например : дробь 6 / 10 и обьясните как вы решили пож.

Просто завтро контролька.

Видео:Как сравнить 2 дроби?Скачать

Пожалуйста помогите?

И если можно немного тему обьясните.

Я непоняла просто.

Видео:Уравнения с дробями. Алгебра 7 класс.Скачать

Объясните пожалуйста, что в данной таблице первая колонка N?

Объясните пожалуйста, что в данной таблице первая колонка N?

Перед вами страница с вопросом Обьясните простыми словами «Перекрёстное правило»?, который относится к категории Математика. Уровень сложности соответствует учебной программе для учащихся 5 — 9 классов. Здесь вы найдете не только правильный ответ, но и сможете ознакомиться с вариантами пользователей, а также обсудить тему и выбрать подходящую версию. Если среди найденных ответов не окажется варианта, полностью раскрывающего тему, воспользуйтесь «умным поиском», который откроет все похожие ответы, или создайте собственный вопрос, нажав кнопку в верхней части страницы.

Ответ : 1 / 5 = 0, 2 тонныПошаговое объяснение : 1 день — продали 2 / 15 тонны овощей. 2 день — продали на 1 / 21 тонны больше, то есть 2 / 15 + 1 / 21 = = 2 / (3 * 5) + 1 / (3 * 7) = (2 * 7) / (3 * 5 * 7) + 5 / (3 * 5 * 7) = (14 + 5) / 105 = 19 / 1..

3 * 4 + 1 * 3 + 1 * 2 = 17 — различных способов.

Основные приемы решения уравнений.

1. Перенос слагаемых из одной части уравнения в другую.

Переход от уравнения

f(x) = g(x) + m(x) (1)
к уравнению

f(x) — m(x) = g(x) (2)
называют переносом слагаемых из одной части уравнения в другую.

Перенос слагаемых из одной части уравнения в другую — это преобразование уравнения всегда приводит к равносильному уравнению, т. е., каковы бы ни были функции f(х), m(х), g(x), мы имеем (1)(2).

В самом деле, пусть a — корень уравнения (1), т. е. соотношение

f(a) + m(a) = g(a) = g(a) + m(a) (3)
представляет собой верное числовое равенство. Это означает, что ринадлежит области определения каждой из функций f<x), m(x), g(x), т. е. определены числа f(a), m(a), g(a), и
2) эти числа связаны соотношением (3).

Прибавляя к обеим частям равенства (3) число -m(a), получаем
f(a) — m(a)+ m(a) = g(a) — m(a),
или
f(a) = g(a) — m(a) — m(a) = g(a) (4)
(поскольку для любого числа b = m(a) верно b — b = 0). Таким образом, (4) есть верное числовое равенство. Но это означает, что a есть корень уравнения (2). Итак, каждый корень уравнения (1) является также корнем уравнения (2), т. е. (1)(2). Аналогично доказывается, что (2)(1). Итак, мы доказали, что при переносе любого слагаемого из одной части уравнения в другую с противоположным знаком получается равносильное уравнение.

В частности, мы можем, если нужно, перенести все слагаемые в одну часть уравнения. Иначе говоря,

f(x) = g(x) f(x) — g(x) = 0

что является частным случаем эквивалентности (1)(2). Мы видим, что любое уравнение с одним неизвестным можно заменить эквивалентным уравнением вида h(х) = 0, т. е. уравнением, в левой части которого стоит некоторая функция, а правая часть равна нулю. Указанное преобразование (перенос членов из одной части уравнения в другую) применяется при решении уравнений чрезвычайно часто. Например, при решении иррациональных уравнений применяется «уединение радикала», т. е. перенос всех членов, кроме одного, имеющего радикал (корень n-ой степени), в другую часть уравнения.

Подчеркнем, что в этом пункте шла речь только о перенесении членов из одной части уравнения в другую без последующего приведения подобных членов (если таковые имеются).

Приведение подобных членов является новым преобразованием (которое может вызвать появление посторонних корней).

2. Приведение подобных членов.

Переход от уравнения

f(x) + m(x) — m(x) = g(x) (5)
к уравнению

f(x) = g(x) (6),
называют приведением подобных слагаемых.

Прежде чем рассматривать переход от уравнения (5) к уравнению (6), сделаем следующее замечание. Согласно сказанному в предыдущем пункте уравнеПрежде чем рассматривать переход от уравнения (5) к уравнению (6), сделаем следующее замечание. Согласно сказанному в предыдущем пункте уравнение (5) равносильно уравнению

f(x) + m(x) = g(x) + m(x) (7).

Поэтому переход от уравнения (1) к уравнению (2) означает то же самое, что и переход от уравнения ( 7 ) к уравнению (2), т. е. во всех рассуждениях уравнение (1) можно заменять равносильным ему уравнением (7). Таким образом, сказанное в этом пункте будет относиться не только к приведению подобных членов в одной части уравнения, но и к вычеркиванию (взаимному уничтожению) одинаковых слагаемых в левой и правой частях. Прежде чем сформулировать общее утверждение, относящееся к переходу от уравнения (1) к уравнению (2) или, что то же самое, от уравнения (7) к уравнению (2), рассмотрим следующие примеры.

Пример 1.. слагаемого — х и — 2 получается равносильное уравнение х 4 = х 2 .

Пример 2.
x 2 + lgx = x + lgx х 2 = х. Уравнение x 2 = х имеет корня х₁ = 1, х₂ = 0, тогда как уравнение x 2 + lgx = x + lgx имеет единственный корень х = 1 (число х = 0 не является корнем уравнения x 2 + lgx = x + lgx, так при х = 0 левая и правая части этого уравнения не определены). Таким образом, уравнение х 2 = х не равносильно уравнению х 2 + lgx = x + lgx, а лишь является следствием этого уравнения. Появление постороннего корня х = 0 при переходе от уравнения x 2 + lgx = x + lgx к уравнению х 2 = х связано с тем, что при этом переходе расширяются множества на которых были определены функции, стоящие в левой и правой частях первого уравнения: в уравнении x 2 + lgx = x + lgx левая и правая части определены при х > 0, а в уравнении х 2 = х,при всех х. Очевидно, обратный переход, т. е. переход от уравнения х 2 = х к уравнению х 2 + lg х = х + lgx вообще недопустим, так как этот переход ведет к потере корня х = 0.

Обозначим через М множество, на котором определены функции f(х) и g(x), стоящие в левой и правой частях уравнения f(x) = g(x) (т.е. пересечение областей определения функций f (х) и g(x). Тогда, если множество М содержится в области определения функции m(х), то уравнение f(x) + m(x) — m(x) = g(x) равносильно уравнению f(x) =g(x). При этих условиях f(x) + m(x) = g(x) + m(x)f(x) = g(x).

3. Умножение обеих частей уравнения на одно и то же выражение.

Переход от уравнения

f(x) = g(x) (8)
к уравнению

f(x)p(x) = g(x)p(x). (9)
называют умножением обеих частей уравнения на одно и тоже выражение.

По поводу этого перехода можно высказать следующие утверждения:

1) Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x) (иначе говоря, Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x)), то уравнение (9) является следствием уравнения (8) или (8)(9)

2) Если в каждой точке, где определены обе функции f(x), g(x) определена также и функция p(x) и в каждой точке указанного множества функция p(x) отлична от нуля, то уравнения (8) и (9) равносильны, т. е. (8)(9).

Заметим, что в общем случае переход от уравнения (9) к уравнению (8) может привести как к появлению посторонних корней, так и к потере корней.

Рассмотрим уравнение x 2 — x = 0. Умножив обе части этого уравнения на, мы получим уравнение= 0, которое не является следствием исходного. В самом деле, исходное уравнение имеет корни х₁ = 0, х₂ = 1, а уравнение= 0 — лишь корень х = 1. Потеря корня связана с тем, что функция — не определена при. х = 0, а как раз это значение х является корнем заданного уравнения.

Такой переход применяется довольно часто при решении уравнений. Естественно, возникает вопрос: можно ли утверждать, что уравнение (*) равносильно дизъюнкции уравнений (**)

Иными словами, можно ли получить «множество всех корней уравнения (*), решив все уравнения (**) и объединив их корни? Ответ на этот вопрос дает следующая теорема.

Эта теорема лежит в основе часто применяемого метода разложения уравнения на множители.

Пример 4. x 6 + 3x 5 — x 4 — 3x 3 = 0,

x 3 (x 3 + 3x 2 — x — 3) =0,

x 3 ((x 3 + 3x 2 ) — (x + 3)) =0,

x 3 (x 2 (x + 3) — (x + 3)) =0,

x 3 (x + 3)(x 2 — 1) =0,

x 3 (x + 3)(x — 1)(x + 1) =0.

Уравнение x 6 +3x 5 — x 4 — 3x 3 = 0 равносильно дизъюнкции уравнений x 3 = 0, x + 3 =0, x + 1 = 0, x — 1 = 0 и имеет следующие корни:

Следующий пример показывает, что в общем случае уравнение (*) не равносильно дизъюнкции уравнений (**).

Пример 5. Пусть f₁(х) = х 2 — 1, f₂(х) =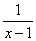. Тогда уравнение f₂(х) = 0 не имеет корней, уравнение f₁(х) = 0 имеет два корня х₁ = 1, х₂ = — 1, а уравнение f₁(х) f₂(х) = 0 имеет только один корень х₁ = -1, так как при х = 1 левая часть этого уравнения не определена.

Теорема 2. Каждый корень уравнения f₁(x)·f₂(x)·. ·f_n(x) = 0 является корнем одного из уравнений f₁(x) = 0, f₂(x) = 0. f_n(x) = 0.

Иначе говоря, дизъюнкция уравнений (**) есть следствие уравнения (*). Из этой теоремы вытекает, что если мы найдем все корни уравнений (**), то среди этих корней будут содержаться все корни уравнения (*) и, быть может, некоторые числа, не являющиеся корнями уравнения (*). Посторонними для уравнения (*) будут те значения х, полученные при решении уравнений (**), для которых хотя бы одна из функций f₁(х), f₂(x), . f_n(x) не определена.

3 а м е ч а н и е. Выше было отмечено, что переход от уравнения
f(x)p(x) = g(x)p(x) к уравнению f(x) = g(x) в общем случае недопустим.

При решении уравнения обычно поступают так. Вместо уравнения
f(x)p(x) = g(x)p(x) рассматривают уравнение (f(x)-g(x))p(x)=0, которое эквивалентно исходному уравнению, т. е. уравнению f(x)p(x) = g(x)p(x).

В свою очередь дизъюнкция уравнений f(x) — g(x) = 0, p(x) = 0 является следствием уравнения (f(x) — g(x))p(x) = 0. Таким образом, если мы решим уравнения f(x) — g(x) = 0, p(x) = 0, а звтем объединим их корни, и проверкой (подстановкой в уравнение (f(x)p(x) = g(x)p(x) отсеем лишние корни, то тем самым мы найдем все корни искомого уравнения.

Пример 6. sinx·ctg2x·arcsin(x — 1)·lg(x — 1) = 0.

Решая каждое уравнение в отдельности, имеем следующее:

sinx = 0, корни этого уравнения x =k, где kZ;

ctg2x = 0, корни этого уравнения: x =+pn, где nZ;

arcsin(x — 1) = 0, корни этого уравнения: x = 1;

lg(x — 1) = 0, корни этого уравнения: x = 2

Те из этих корней, которые принадлежат области определения левой части исходного уравнения, являются корнями исходного урапвнения.

Запишем области определения функций:

M₁ = D(sinx) = (-; +),

M₂ = D(ctg2x) = (-; +), x+m, mZ,

M₄ = D(lg(x — 1)) = (1; +).

Область определения M левой части исходного уравнения является пересечение множеств M₁, M₂, M₃, M₄.
M = (1; )(; 2]. Из всех найденных корней множеству М, т. е. области определения левой части исходного уравнения, принадлежит корень 2. Корнем исходного уравнения является число 2.

5. Переход от уравнения f(x)= g(x) к уравнению [f(х)] n = [g(х)] n . Такой переход нередко используется при решении уравнений, особенно при решении иррациональных уравнений.

Пусть функции f(х) и g(x) определены на множестве М (т. е. множество М содержится в области определения каждой из функций f(x), g(x)) и n — произвольное натуральное число. Будем предполагать, что М — некоторое множество действительных чисел и что на этом множестве функции f (х) и g(x) принимают действительные значения. Мы можем утверждать следующее:

В общем случае переход от уравнения [f(x>] n = [g(x)] n к уравнению f(x) = g(x) не допустим, так как такой переход может привести к потере корней.

Пример 7. Решите уравнение= x + 1.

Решение. Возводя обе части уравнения в квадрат, получим уравнение

2x 2 + 5x — 3 = x 2 + 2x + 1, являющееся следствием уравнения. Полученное уравнение равносильно уравнению х 2 + 3х — 4 = 0, корнями которого являются числа х₁ = -4, х₂ = 1. Проверка показывает, что корень x₁ = — 4 является посторонним для уравнения исходного иррационального уравнения, а корень х₂= 1 удовлетворяет уравнению обоим уравнениям. Таким образом, уравнение исходное заданное уравнение имеет единственный корень х = 1.

Более общим, чем рассмотренный в пятом примере, является переход от уравнения f(x) = g(x) к уравнению m(f(x)) = m(g(x)), где m(t) — некоторая заданная функция. Заметим сразу, что в общем случае такой переход недопустим. В самом деле, пусть Е₁ и Е₂,—множества значений соответственно функций f(x) и g(x) и Е — общая часть (т. е. пересечение) множеств E₁ и Е₂. Если функция m(t) не определена на множестве Е, то уравнение m(f(x)) = m(g(x))не имеет решений, в то время как исходное уравнение могло иметь решения. Если же множество Е содержится в области определения функции m(t), то, как легко доказать, f(x) = g(x)m(f(x)) = m(g(x)). Если же, кроме того, функция m(t) монотонна, то f(x) = g(x) m(f(x) = m(g(x)).

Пример 8. Уравнение — x 4 = — x 2 имеет корни х₁ = 0, x₂ = 1, х₃ = — 1, а уравнение
lg(-х 2 ) = lg(-х 4 ) не имеет решений. Произошло это потому, что обе функции
f<x)= -x 2 , g(x) = — x 4 принимают значения, принадлежащие множеству Е = (-; 0], а на этом множестве функция lgx не определена.

6. Метод замены неизвестного. Метод замены неизвестного применяется при решении уравнений вида f(g(x)) = 0.

Он основывается на следующей теореме.

Теорема 3. Рассмотрим уравнение f(t) = 0, где t — вспомогательное неизвестное, и пусть t₁, t₂,₃. t_k — все корни уравнения. Тогда для решения уравнения f(g(x)) = 0 достаточно найти все корни каждого из уравнений g(x) = t_m (m = l, 2, . k) и объединить множества корней этих уравнений.

Иначе говоря, f(g(x)) = 0g(x) = t₁, g(x) = t₂, . g(x) = t_k.

Эта теорема позволяет свести решение уравнения вида f(g(x))= 0 к решению нескольких более простых уравнений f(t) = 0, g(x) = t_k, где k = 1, 2. m.

Обычно эта теорема применяется следующим образом.

Дано некоторое уравнение f(x) = 0. Задача заключается в том, чтобы умело подобрать функцию g(x), позволяющую ввести новое неизвестное t = g(x), и затем выразить функцию f(х) через t, т. е. представить ее в виде f(x) = h(g(x)). В результате данное уравнение запишется в виде h(g(x))= 0, и для его решения можно будет применить доказанную теорему. Такой прием решения уравнений и называется методом замены неизвестного (поскольку вначале решается уравнение f(t) = 0, в котором неизвестное х заменено новым, вспомогательным неизвестным t.

Пример 9. Решить уравнение х 2 += х —+ 4.

Введем новое неизвестное t = х —.

Тогда заданное уравнение примет вид t 2 — t = 0.

Уравнение t 2 — t = 0 имеет корни t₁ = 0, t₂ = 1. Следовательно, х 2 += х —+ 4х —= 0, х —= 1.

Решив теперь уравнения

х —= 0, x₁ =, x₂ = —.

х —= 1, x₃ = — 1, x₄ = 2.

Исходное уравнение имеет четыре корня: — 1, —,, 2.