Результирующая (зависимая, эндогенная) переменная Y
Она характеризует результат или эффективность функционирования экономической системы. Значения ее формируются в процессе и внутри функционирования этой системы под воздействием ряда других переменных и факторов, часть из которых поддается регистрации, управлению и планированию. В регрессионном анализе результирующая переменная играет роль функции, значение которой определяется значениями объясняющих переменных, выполняющих роль аргументов. По своей природе результирующая переменная всегда случайна (стохастична).
Объясняющие (экзогенные, независимые) переменные X
Это — переменные, которые поддаются регистрации и описывают условия функционирования реальной экономической системы. Они в значительной мере определяют значения результирующих переменных. Обычно часть из них поддается регулированию и управлению. Значение этих переменных могут задаваться вне анализируемой системы. Поэтому их называют экзогенными. Еще их называют факторными признаками. В регрессионном анализе это аргументы результирующей функции Y. По своей природе они могут быть как случайными, так и неслучайными.
Любая эконометрическая модель предназначена для объяснения значений текущих эндогенных переменных (одной или нескольких) в зависимости от значений заранее определенных переменных.
Переменные, выступающие в системе в роли факторов-аргументов, или объясняющих переменных называют предопределенными. Множество предопределенных переменных формируется из всех экзогенных переменных и так называемых лаговых эндогенныхпеременных, т. е. таких эндогенных переменных, значения которых входят в уравнения анализируемой эконометрической системы измеренными в прошлые моменты времени, а, следовательно, являются уже известными, заданными.
Типы эконометрических моделей
Можно выделить три основных класса моделей, которые применяются для анализа и прогнозирования экономических систем
· модели временных рядов;
· регрессионные модели с одним уравнением;
· системы одновременных уравнений.
Модели временных рядов
Модели временных рядов представляют собой модели зависимости результативного признака от времени.
К ним относятся
· модели кривых роста (трендовые модели),
· модели авторегрессии и скользящего среднего.
С помощью таких моделей можно решать задачи прогнозирования объема продаж, спроса на продукцию, краткосрочного прогноза процентных ставок и др.
Регрессионные модели с одним уравнением
В регрессионных моделях зависимая (объясняемая) переменная Y может быть представлена в виде функции f (X1, X2, X3, … Xk), где 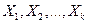
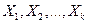
Примеры задач,решаемых с помощьюрегрессионных моделей.
- Исследование зависимости заработной платы (Y) от возраста (X1), уровня образования (X2), пола (X3), стажа работы (X4) (
).
- Прогноз и планирование выпускаемой продукции по факторам производства (производственная функция Кобба – Дугласа
означает, что объем выпуска продукции (Y), является функцией количества капитала ( K ) и количества (L) труда).
- Прогноз объемов потребления продукции или услуг определенного вида (кривая Энгеля
, где Y —удельная величина спроса, Х — среднедушевой доход).
Системы эконометрических уравнений
Сложные социально-экономические явления иногда невозможно адекватно описать с помощью только одного соотношения (уравнения). Модели с одним уравнением не отражают взаимосвязей между объясняющими переменными или их связей с другими переменными. Кроме того, некоторые переменные могут оказывать взаимные воздействия и трудно однозначно определить, какая из них является зависимой, а какая независимой переменной. Поэтому при построении эконометрической модели прибегают к системам уравнений.
Для оценивания систем одновременных уравнений используются специальные методы.
Эконометрические методы используются в экономических и технико-экономических исследованиях, работах по управлению (менеджменту).
Каждой области экономических исследований, связанной с анализом эмпирических данных, как правило, соответствуют свои эконометрические модели.
Дата добавления: 2016-06-15 ; просмотров: 3324 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Что такое объясняющая переменная в уравнении
Рассмотрим модели, в которых зависимая переменная выражается в виде фиктивной (двоичной) переменной. Объясняющие переменные могут быть как количественными, так и качественными. [c.268]
На рис. 16.7 видно, что, во-первых, даже внутри группы с одним доходом расходы людей различны, что объясняется различием вкусов, потребностей, количеством членов в семье и другими факторами, которые не входят в число переменных, объясняющих расходы, и представляемыми в виде случайного (по отношению к доходам) компонента расходов. Во-вторых, можно заметить, что, в среднем, расходы растут с увеличением доходов. [c.305]
Сравнение с включением в уравнение в число объясняющих переменных объясняемой переменной, взятой с лагом, требует корректировки коэффициентов на величину соответствующего мультипликатора. [c.161]
Если мы можем рассчитать, хотя бы приблизительно, кривые предложения и спроса на определенный товар, мы можем вычислить равновесную цену, приравнивая предложение и спрос. Если мы также знаем, насколько предложение и спрос зависят от других экономических переменных величин (таких, как доход или цены на другие товары), мы можем вычислить, как будут меняться равновесные цена и объем продаж при изменении других переменных. Это одно из средств, объясняющих или прогнозирующих поведение на рынке. [c.64]
В рыночной экономике ситуация существенным образом меняется. Появляются предприятия, которые вынуждены самостоятельно планировать свои действия в условиях конкурентной среды. Роль планово-аналитической функции в системе управления предприятием коренным образом преобразуется — контрольно-аналитический и объясняющий аспекты теряют свою исключительную значимость, более важными становятся коммуникативный и прогнозно-ориентирующий аспекты. Логика перемен достаточно очевидна. [c.331]
При построении моделей необходимо учитывать наличие авторегрессии, т.е. тот факт, что объясняющими переменными являются не только те, что мы включаем в модель, но и время (обозначим t), причем в значительной степени. Поэтому следует включать в уравнение регрессии и фактор t. [c.672]
На основе F-критерия принимаются решения о форме уравнения регрессии, о статистической значимости той или иной объясняющей переменной при построении многофакторного уравнения регрессии (см. гл. 8) и др. [c.217]
Заметим, что в принципе, как уже отмечалось, круг факторов для х и w может частично совпадать. В случае непосредственной связи между х и w, та из переменных, которая является независимой, может включаться в регрессию другой (зависимой) переменной. Положим, что круг объясняющих переменных для х и w остался неизменным в отчетном периоде по сравнению с базисным. Принимая регрессии линейными, имеем по две регрессии для х и w, описывающих базисное и отчетное состояние дг и w. [c.410]
По данным отчетного и базисного периодов можно построить регрессии — обязательно с одним и тем же набором объясняющих переменных [c.422]
Средняя величина, у, может изменяться, во-первых, за счет изменений средних значений объясняющих переменных Зсх- в отчетном [c.422]
Мы ставим задачу определить цену — величину, формируемую под воздействием некоторых факторов (года выпуска, пробега и т. д.). Такие зависимые величины обычно называются зависимыми (объясняемыми) переменными, а факторы, от которых они зависят, — объясняющими. [c.9]
Формируя общее мнение о состоянии рынка, мы обращаемся к интересующему нас объекту и получаем ожидаемое значение зависимой переменной при заданных значениях объясняющих переменных. [c.9]
Каково практическое применение полученного результата Очевидно, во-первых, он позволяет понять как именно формируется рассматриваемая экономическая переменная — цена на автомобиль. Во-вторых, он дает возможность выявить влияние каждой из объясняющих переменных на цену автомобиля (так, в данном случае цена нового автомобиля (при J i=0, X2=0) 18000 у.е., при этом только за счет увеличения срока эксплуатации на 1 год цена автомобиля уменьшается в среднем на 1000 у.е., а только за счет увеличения пробега на 1 тыс. км — на 0,5 у.е.). В третьих, что, пожалуй, наиболее важно, этот результат позволяет прогнозировать цену на автомобиль, [c.10]
Пусть имеется р объясняющих переменных Х, . Хри зависимая переменная Y. Переменная Y является случайной величиной, имеющей при заданных значениях факторов некоторое распределение. Если случайная величина Y непрерывна, то можно считать, что ее распределение при каждом допустимом наборе значений факторов (х, х . хр) имеет условную плотность [c.11]
Объясняющие переменные Xj(j = . />) могут считаться как случайными, так и детерминированными, т. е. принимающими определенные значения. Проиллюстрируем этот тезис на уже рассмотренном примере продажи автомобилей. Мы можем заранее определить для себя параметры автомобиля и искать объявления о продаже автомобиля с такими параметрами. В этом случае неуправляемой, случайной величиной остается только зависимая переменная — цена. Но мы можем также случайным образом выбирать объявления о продаже, в этом случае параметры автомобиля — объясняющие переменные — также оказываются случайными величинами. [c.11]
Классическая эконометрическая модель рассматривает объясняющие переменные Xj как детерминированные, однако, как мы увидим в дальнейшем, основные результаты статистического исследования модели остаются в значительной степени теми же, что и в случае, если считать X/ случайными переменными. [c.11]
Объясненная часть — обозначим ее Ye — в любом случае представляет собой функцию от значений факторов — объясняющих переменных [c.12]
Однако может оказаться, что данные о доходе, полученные в результате опроса, на самом деле являются искаженными, — например, в среднем заниженными, т.е. объясняющие переменные измеряются с систематическими ошибками. В этом случае люди, действительно обладающие доходом X, будут на самом деле тратить на исследуемый товар в среднем величину, меньшую, чем ДА), т.е. в рассмотренном примере объ- [c.12]
Систематические ошибки измерения объясняющих переменных — одна из возможных причин того, что эконометрическая модель не является регрессионной. В экономических исследованиях подобная ситуация встречается достаточно часто. Одним из возможных путей устранения этого, как правило, довольно неприятного обстоятельства, является выбор других объясняющих переменных (эти вопросы рассматриваются в гл. 8 настоящего учебника). [c.13]
Рассмотрим равенство Y = Мх (Y) + Е и возьмем от обеих частей математическое ожидание при заданном наборе значений объясняющих переменных X. В этом случае Мх (Y) есть числовая величина, равная своему математическому ожиданию, и мы получаем равенство [c.13]
Чтобы получить достаточно достоверные и информативные данные о распределении какой-либо случайной величины, необходимо иметь выборку ее наблюдений достаточно большого объема. Выборка наблюдений зависимой переменной 7 и объясняющих переменных Xj (j = 1. р) является отправной точкой любого эконометрического исследования. [c.13]
Такие выборки представляют собой наборы значений (хц,. , Xjp, У,), где / = 1. л р — количество объясняющих переменных, и — число наблюдений. [c.13]
Как правило, число наблюдений п достаточно велико (десятки, сотни) и значительно превышает число р объясняющих переменных. Проблема, однако, заключается в том, что наблюдения yi, рассматриваемые в разных выборках как случайные величины YJ и получаемые при различных наборах значений объясняющих переменных X/, имеют, вообще говоря, различное распределение. А это означает, что для каждой случайной величины YI мы имеем всего лишь одно наблюдение. Разумеется, на основании одного наблюдения никакого адекватного вывода о распределении случайной величины сделать нельзя, и нужны дополнительные предположения. [c.14]
Пусть определен характер экспериментальных данных и выделен определенный набор объясняющих переменных. [c.17]
Особенностью этих систем является то, что каждое из уравнений системы, кроме своих объясняющих переменных, может включать объясняемые переменные из других уравнений. Таким [c.19]
В другой модели спроса и предложения в качестве объясняющей предложение Qf переменной может быть не только цена товара Р в данный момент времени t, т.е. Р но и цена товара в предыдущий момент времени Р,- ь т.е. лаговая эндогенная переменная [c.20]
В регрессионном анализе рассматриваются односторонняя зависимость случайной переменной Y от одной (или нескольких) неслучайной независимой переменной X. Такая зависимость может возникнуть, например, в случае, когда при каждом фиксированном значении X соответствующие значения Y подвержены случайному разбросу за счет действия ряда неконтролируемых факторов. Такая зависимость Гот X (иногда ее называют регрессионной) может быть также представлена в виде модельного уравнения регрессии 7 по X (3.1). При этом зависимую переменную У называют также функцией отклика, объясняемой, выходной, результирующей, эндогенной переменной, результативным признаком, а независимую переменную X — объясняющей, входной, [c.51]
В модели (3.22) возмущение е/ (или зависимая переменная yi) есть величина случайная, а объясняющая переменная xt — величина неслучайная . [c.61]
Очевидно, что при заданных значениях jq, X2. х объясняющей переменной X и постоянной дисперсии ст2 функция правдоподобия L достигает максимума, когда показатель степени при е будет минимальным по абсолютной величине, т. е. при условии минимума функции [c.63]
Из формул (3.33) и (3.34) видно, что величина (длина) доверительного интервала зависит от значения объясняющей переменной х». при х = х она минимальна, а по мере удаления х от х величина доверительного интервала увеличивается (рис. 3.6). Таким образом, прогноз значений (определение неизвестных значений) зависимой переменной Y по уравнению регрессии оправдан, если [c.66]
Проверить значимость уравнения регрессии — значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. [c.70]
Средние квадраты s и s2 (табл. 3.3) представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессий или объясняющей переменной X и воздействием неучтенных случайных факторов и ошибок т — число оцениваемых параметров уравнения регрессии п — число наблюдений. [c.72]
При отсутствии линейной зависимости между зависимой и объясняющими(ей) переменными случайные величины SR — QR l(m 1) и s2=Qe/(n-m) имеют х2-распределение соответственно с т—1 и п—т степенями свободы, а их отношение — -распределение с теми же степенями свободы (см. 2.3). Поэтому уравнение регрессии значимо на уровне а, если фактически наблюдаемое значение статистики [c.72]
Величина R2 показывает, какая часть (доля) вариации зависимой переменной обусловлена вариацией объясняющей переменной. [c.75]
Это означает, что вариация зависимой переменной Y — сменной добычи угля на одного рабочего — на 75,0% объясняется изменчивостью объясняющей переменной X— мощностью пласта. Р> [c.76]
Для оценки параметров всей системы уравнений в целом используется трехшаговый МНК. К его применению прибегают в тех случаях, когда переменные, объясняемые в одном уравнении, в другом выступают в роли объясняющих. Так было в нашем примере с моделью спроса и предложения, где спрос и предложение, с одной стороны, определяются рыночной ценой, а с другой стороны, предложение должно быть равно спросу. При расчете параметров таких моделей необходимо учитывать всю систему соотношений. В трех-шаговом методе это реализуется в три этапа. Первые два из них похожи надвухшаговый метод, т.е. производится оценка параметров в уравнениях с лаговыми переменными. В нашем примере лаго- [c.358]
Верхняя строка корректированный / -квадрат = 0,872390 вторая строка / -квадрат = 0,897912 третья строка множественный R = 0,947582. Затем приводится таблица дисперсионного анализа, в которой указываются источники вариации объясненная сумма квадратов отклонений значений, рассчитанных по уравнению регрессии, от среднего значения DlfnM il = Z(p/ — у)2 = 662 772,98 при числе степеней свободы, равном числу объясняющих переменных dfk = 3 остаточная — отклонения фактических значений от расчетных Dwm Z(y/ — у)2 = 75353,96 при числе степеней свободы, равном df=n-k-, df= 2 общая — ZO/ — У = 738 126,94, при числе степеней свободы df = п — 1, df = 15. Затем приводится средний квадрат отклонений s = Д , с//)6ы, , = 662772,98 3 = 220924,3 s г = D,Km dfwm, = 75353,96 12 = 6279,5. Далее указано их отношение, т. е. 5, /г2 = F-критерию. Наконец, указывается вероятность ошибочного решения, т. е. нулевого / 2, равная 0,000003171. [c.277]
До сих пор мы рассматривали эконометрические модели, задаваемые уравнениями, выражающими зависимую (объясняемую) переменную через объясняющие переменные. Однако реальные экономические объекты, исследуемые с помощью эко-нометрических методов, приводят к расширению понятия эко-нометрической модели, описываемой системой регрессионных уравнений и тождеств1. [c.19]
При выборе экономических переменных необходимо теоретическое обоснование каждой переменной (при этом рекомендуется, чтобы число их было не очень большим и, как минимум, в несколько раз меньше числа наблюдений). Объясняющие переменные не должны быть связаны функциональной или тесной корреляционной зависимостью, так как это может привести к невозможности оценки параметров модели или к получению неустойчивых, не имеющим реального смысла оценок,- т. е. к явлению мулътиколлинеарности (см. об этом гл. 5). [c.21]
Смотреть страницы где упоминается термин Переменная объясняемая
Эконометрика начальный курс (2004) — [ c.29 ]
Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Введение в множественную регрессию
Рассматривая простую регрессию, мы сосредоточили внимание на модели, в которой для предсказания значения зависимой переменной, или отклика Y, использовалась лишь одна независимая, или объясняющая, переменная X. Однако во многих случаях можно разработать более точную модель, если учесть не одну, а несколько объясняющих переменных. По этой причине мы рассмотрим в этой заметке модели множественной регрессии, в которых для предсказания значения зависимой переменной используется несколько независимых переменных. [1]
Материал будет проиллюстрирован сквозным примером: прогнозирование объемов продаж компании OmniPower. Представьте себе, что вы — менеджер по маркетингу в крупной национальной сети бакалейных магазинов. В последние годы на рынке появились питательные батончики, содержащие большое количество жиров, углеводов и калорий. Они позволяют быстро восстановить запасы энергии, потраченной бегунами, альпинистами и другими спортсменами на изнурительных тренировках и соревнованиях. За последние годы объем продаж питательных батончиков резко вырос, и руководство компании OmniPower пришло к выводу, что этот сегмент рынка весьма перспективен. Прежде чем предлагать новый вид батончика на общенациональном рынке, компания хотела бы оценить влияние его стоимости и рекламных затрат на объем продаж. Для маркетингового исследования были отобраны 34 магазина. Вам необходимо создать регрессионную модель, позволяющую проанализировать данные, полученные в ходе исследования. Можно ли применить для этого модель простой линейной регрессии, рассмотренную в предыдущей заметке? Как ее следует изменить?
Модель множественной регрессии
Для маркетингового исследования в компании OmniPower была создана выборка, состоящая из 34 магазинов с приблизительно одинаковыми объемами продаж. Рассмотрим две независимые переменные — цена батончика OmniPower в центах (Х1) и месячный бюджет рекламной кампании, проводимой в магазине, выраженный в долларах (Х2). В этот бюджет входят расходы на оформление вывесок и витрин, а также на раздачу купонов и бесплатных образцов. Зависимая переменная Y представляет собой количество батончиков OmniPower, проданных за месяц (рис. 1).
Рис. 1. Месячный объем продажа батончиков OmniPower, их цена и расходы на рекламу
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Интерпретация регрессионных коэффициентов. Если в задаче исследуются несколько объясняющих переменных, модель простой линейной регрессии можно расширить, предполагая, что между откликом и каждой из независимых переменных существует линейная зависимость. Например, при наличии k объясняющих переменных модель множественной линейной регрессии принимает вид:
где β0 — сдвиг, β1 — наклон прямой Y, зависящей от переменной Х1, если переменные Х2, Х3, … , Хk являются константами, β2 — наклон прямой Y, зависящей от переменной Х2, если переменные Х1, Х3, … , Хk являются константами, βk — наклон прямой Y, зависящей от переменной Хk, если переменные Х1, Х2, … , Хk-1 являются константами, εi — случайная ошибка переменной Y в i-м наблюдении.
В частности, модель множественной регрессии с двумя объясняющими переменными:
где β0 — сдвиг, β1 — наклон прямой Y, зависящей от переменной Х1, если переменная Х2 является константой, β2 — наклон прямой Y, зависящей от переменной Х2, если переменная Х1 является константой, εi — случайная ошибка переменной Y в i-м наблюдении.
Сравним эту модель множественной линейной регрессии и модель простой линейной регрессии: Yi = β0 + β1Xi + εi. В модели простой линейной регрессии наклон β1 представляет собой изменение среднего значения переменной Y при изменении значения переменной X на единицу и не учитывает влияние других факторов. В модели множественной регрессии с двумя независимыми переменными (2) наклон β1 представляет собой изменение среднего значения переменной Y при изменении значения переменной X1 на единицу с учетом влияния переменной Х2. Эта величина называется коэффициентом чистой регрессии (или частной регрессии).
Как и в модели простой линейной регрессии, выборочные регрессионные коэффициенты b0, b1, и b2 представляют собой оценки параметров соответствующей генеральной совокупности β0, β1 и β2.
Уравнение множественной регрессии с двумя независимыми переменными:
(3) 
Для вычисления коэффициентов регрессии используется метод наименьших квадратов. В Excel можно воспользоваться Пакетом анализа, опцией Регрессия. В отличие от построения линейной регрессии, просто задайте в качестве Входного интервала Х область, включающую все независимые переменные (рис. 2). В нашем примере это $C$1:$D$35.
Рис. 2. Окно Регрессия Пакета анализа Excel
Результаты работы Пакета анализа представлены на рис. 3. Как видим, b0 = 5 837,52, b1 = –53,217 и b2 = 3,163. Следовательно, 
Рис. 3. Множественная регрессия исследования объем продажа батончиков OmniPower
Выборочный наклон b0 равен 5 837,52 и является оценкой среднего количества батончиков OmniPower, проданных за месяц при нулевой цене и отсутствии затрат на рекламу. Поскольку эти условия лишены смысла, в данной ситуации величина наклона b0 не имеет разумной интерпретации.
Выборочный наклон b1 равен –53,217. Это значит, что при заданном ежемесячном объеме затрат на рекламу увеличение цены батончика на один цент приведет к снижению ожидаемого объема продаж на 53,217 штук. Аналогично выборочный наклон b2, равный 3,613, означает, что при фиксированной цене увеличение ежемесячных рекламных затрат на один доллар сопровождается увеличением ожидаемого объема продаж батончиков на 3,613 шт. Эти оценки позволяют лучше понять влияние цены и рекламы на объем продаж. Например, при фиксированном объеме затрат на рекламу уменьшение цены батончика на 10 центов увеличит объем продаж на 532,173 шт., а при фиксированной цене батончика увеличение рекламных затрат на 100 долл. увеличит объем продаж на 361,31 шт.
Интерпретация наклонов в модели множественной регрессии. Коэффициенты в модели множественной регрессии называются коэффициентами чистой регрессии. Они оценивают среднее изменение отклика Y при изменении величины X на единицу, если все остальные объясняющие переменные «заморожены». Например, в задаче о батончиках OmniPower магазин с фиксированным объемом рекламных затрат за месяц продаст на 53,217 батончика меньше, если увеличит их стоимость на один цент. Возможна еще одна интерпретация этих коэффициентов. Представьте себе одинаковые магазины с одинаковым объемом затрат на рекламу. При уменьшении цены батончика на один цент объем продаж в этих магазинах увеличится на 53,217 батончика. Рассмотрим теперь два магазина, в которых батончики стоят одинаково, но затраты на рекламу отличаются. При увеличении этих затрат на один доллар объем продаж в этих магазинах увеличится на 3,613 штук. Как видим, разумная интерпретация наклонов возможна лишь при определенных ограничениях, наложенных на объясняющие переменные.
Предсказание значений зависимой переменной Y. Выяснив, что накопленные данные позволяют использовать модель множественной регрессии, мы можем прогнозировать ежемесячный объем продаж батончиков OmniPower и построить доверительные интервалы для среднего и предсказанного объемов продаж. Для того чтобы предсказать средний ежемесячный объем продаж батончиков OmniPower по цене 79 центов в магазине, расходующем на рекламу 400 долл. в месяц, следует применить уравнение множественной регрессии: Y = 5 837,53 – 53,2173*79 + 3,6131*400 = 3 079. Следовательно, ожидаемый объем продаж в магазинах, торгующих батончиками OmniPower по цене 79 центов и расходующих на рекламу 400 долл. в месяц, равен 3 079 шт.
Вычислив величину Y и оценив остатки, можно построить доверительные интервалы, содержащие математическое ожидание и предсказанное значение отклика. Ранее мы рассмотрели эту процедуру в рамках модели простой линейной регрессии. Однако построение аналогичных оценок для модели множественной регрессии сопряжено с большими вычислительными трудностями и здесь не приводится.
Коэффициент множественной смешанной корреляции. Напомним, что модель регрессии позволяет вычислить коэффициент смешанной корреляции r 2 . Поскольку в модели множественной регрессии существуют по крайней мере две объясняющие переменные, коэффициент множественной смешанной корреляции представляет собой долю вариации переменной Y, объясняемой заданным набором объясняющих переменных:
где SSR – сумма квадратов регрессии, SST – полная сумма квадратов.
Например, в задаче о продажах батончика OmniPower SSR = 39 472 731, SST = 52 093 677 и k = 2. Таким образом,
Это означает, что 75,8% вариации объемов продаж объясняется изменениями цен и колебаниями объемов затрат на рекламу.
Анализ остатков для модели множественной регрессии
Анализ остатков позволяет определить, можно ли применять модель множественной регрессии с двумя (или более) объясняющими переменными. Как правило, проводят следующие виды анализа остатков:
- Распределение остатков по
(рис. 4).
- Распределение остатков по Х1i (рис. 5).
- Распределение остатков по Х2i (рис. 5).
- Распределение остатков по времени.
Первый график (рис. 4а) позволяет проанализировать распределение остатков в зависимости от предсказанных значений 

Рис. 4. Зависимость остатков от предсказанного значения
Второй и третий график демонстрируют зависимость остатков от объясняющих переменных. Эти графики могут выявить квадратичный эффект. В этой ситуации необходимо добавить в модель множественной регрессии квадрат объясняющей переменной. Эти графики выводятся Пакетом анализа (см. рис. 2), если включить опцию График остатков (рис. 5).
Рис. 5. Зависимость остатков от цены и затрат на рекламу
Четвертый график применяется для проверки независимости данных, собранных в течение определенного времени. Для этого надо наблюдения расположить по времени, и построить зависимость предсказанного значения 
Проверка значимости модели множественной регрессии.
Убедившись с помощью анализа остатков, что модель линейной множественной регрессии является адекватной, можно определить, существует ли статистически значимая взаимосвязь между зависимой переменной и набором объясняющих переменных. Поскольку в модель входит несколько объясняющих переменных, нулевая и альтернативная гипотезы формулируются следующим образом: Н0: β1 = β2 = … = βk = 0 (между откликом и объясняющими переменными нет линейной зависимости), Н1: существует по крайней мере одно значение βj ≠ 0 (мжду откликом и хотя бы одной объясняющей переменной существует линейная зависимость).
Для проверки нулевой гипотезы применяется F-критерий – тестовая F-статистика равна среднему квадрату, обусловленному регрессией (MSR), деленному на дисперсию ошибок (MSE):
где F – тестовая статистика, имеющая F-распределение с k и n – k – 1 степенями свободы, k – количество независимых переменных в регрессионной модели.
Решающее правило выглядит следующим образом: при уровне значимости α нулевая гипотеза Н0 отклоняется, если F > FU(k,n – k – 1), в противном случае гипотеза Н0 не отклоняется (рис. 6).
Рис. 6. Сводная таблица дисперсионного анализа для проверки гипотезы о статистической значимости коэффициентов множественной регрессии
Сводная таблица дисперсионного анализа, заполненная с использованием Пакета анализа Excel при решении задачи о продажах батончиков OmniPower, показана на рис. 3 (см. область А10:F14). Если уровень значимости равен 0,05, критическое значение F-распределения с двумя и 31 степенями свободы FU(2,31) = F.ОБР(1-0,05;2;31) = равно 3,305 (рис. 7).
Рис. 7. Проверка гипотезы о значимости коэффициентов регрессии при уровне значимости α = 0,05, с 2 и 31 степенями свободы
Как показано на рис. 3, F-статистика равна 48,477 > FU(2,31) = 3,305, а p-значение близко к 0,000 2,0395 или р = 0,0000 4,17), гипотеза Н0 отклоняется, следовательно, учет переменной Х1 (цены) значительно улучшает модель регрессии, в которую уже включена переменная Х2 (затраты на рекламу).
Аналогично можно оценить влияние переменной Х2 (затраты на рекламу) на модель, в которую уже включена переменная Х1 (цена). Проведите вычисления самостоятельно. Решающее условие приводит к тому, что 27,8 > 4,17, и следовательно, включение переменной Х2 также приводит к значительному увеличению точности модели, в которой учитывается переменная Х1. Итак, включение каждой из переменных повышает точность модели. Следовательно, в модель множественной регрессии необходимо включить обе переменные: и цену, и затраты на рекламу.
Любопытно, что значение t-статистики, вычисленное по формуле (6), и значение частной F-статистики, заданной формулой (9), однозначно взаимосвязаны:
где а — количество степеней свободы.
Регрессионные модели с фиктивной переменной и эффекты взаимодействия
Обсуждая модели множественной регрессии, мы предполагали, что каждая независимая переменная является числовой. Однако во многих ситуациях в модель необходимо включать категорийные переменные. Например, в задаче о продажах батончиков OmniPower для предсказания среднемесячного объема продаж использовались цена и затраты на рекламу. Кроме этих числовых переменных, можно попытаться учесть в модели расположение товара внутри магазина (например, на витрине или нет). Для того чтобы учесть в регрессионной модели категорийные переменные, следует включить в нее фиктивные переменные. Например, если некая категорийная объясняющая переменная имеет две категории, для их представления достаточно одной фиктивной переменной Xd: Xd = 0, если наблюдение принадлежит первой категории, Xd = 1, если наблюдение принадлежит второй категории.
Для иллюстрации фиктивных переменных рассмотрим модель для предсказания средней оценочной стоимости недвижимости на основе выборки, состоящей из 15 домов. В качестве объясняющих переменных выберем жилую площадь дома (тыс. кв. футов) и наличие камина (рис. 11). Фиктивная переменная Х2 (наличие камина) определена следующим образом: Х2 = 0, если камина в доме нет, Х2 = 1, если в доме есть камин.
Рис. 11. Оценочная стоимость, предсказанная по жилой площади и наличию камина
Предположим, что наклон оценочной стоимости, зависящей от жилой площади, одинаков у домов, имеющих камин и не имеющих его. Тогда модель множественной регрессии выглядит следующим образом:
где Yi — оценочная стоимость i-гo дома, измеренная в тысячах долларов, β0 — сдвиг отклика, X1i,— жилая площадь i-гo дома, измеренная в тыс. кв. футов, β1 — наклон оценочной стоимости, зависящей от жилой площади дома при постоянном значении фиктивной переменной, X1i,— фиктивная переменная, означающая наличие или отсутствие камина, β1 — наклон оценочной стоимости, зависящей от жилой площади дома при постоянном значении фиктивной переменной β2 — эффект увеличения оценочной стоимости дома в зависимости от наличия камина при постоянной величине жилой площади, εi – случайная ошибка оценочной стоимости i-гo дома. Результаты вычисления регрессионой модели представлены на рис. 12.
Рис. 12. Результаты вычисления регрессионой модели для оценочной стоимости домов; получены с помощью Пакета анализа в Excel; для расчета использована таблица, аналогичная рис. 11, с единственным изменением: «Да» заменены единицами, а «Нет» – нулями
В этой модели коэффициенты регрессии интерпретируются следующим образом:
- Если фиктивная переменная имеет постоянное значение, увеличение жилой площади на 1000 кв. футов приводит к увеличению предсказанной средней оценочной стоимости на 16,2 тыс. долл.
- Если жилая площадь постоянна, наличие камина увеличивает среднюю оценочную стоимость дома на 3,9 тыс. долл.
Обратите внимание (рис. 12), t-статистика, соответствующая жилой площади, равна 6,29, а р-значение почти равно нулю. В то же время t-статистика, соответствующая фиктивной переменной, равна 3,1, а p-значение – 0,009. Таким образом, каждая из этих двух переменных вносит существенный вклад в модель, если уровень значимости равен 0,01. Кроме того, коэффициент множественной смешанной корреляции означает, что 81,1% вариации оценочной стоимости объясняется изменчивостью жилой площади дома и наличием камина.
Эффект взаимодействия. Во всех регрессионных моделях, рассмотренных выше, считалось, что влияние отклика на объясняющую переменную является статистически независимым от влияния отклика на другие объясняющие переменные. Если это условие не выполняется, возникает взаимодействие между зависимыми переменными. Например, вполне вероятно, что реклама оказывает большое влияние на объем продаж товаров, имеющих низкую цену. Однако, если цена товара слишком высока, увеличение расходов на рекламу не может существенно повысить объем продаж. В этом случае наблюдается взаимодействие между ценой товара и затратами на его рекламу. Иначе говоря, нельзя делать общих утверждений о зависимости объема продаж от затрат на рекламу. Влияние рекламных расходов на объем продаж зависит от цены. Это влияние учитывается в модели множественной регрессии с помощью эффекта взаимодействия. Для иллюстрации этого понятия вернемся к задаче о стоимости домов.
В разработанной нами регрессионной модели предполагалось, что влияние размера дома на его стоимость не зависит от того, есть ли в доме камин. Иначе говоря, считалось, что наклон оценочной стоимости, зависящей от жилой площади дома, одинаков у домов, имеющих камин и не имеющих его. Если эти наклоны отличаются друг от друга, между размером дома и наличием камина существует взаимодействие.
Проверка гипотезы о равенстве наклонов сводится к оценке вклада, который вносит в модель регрессии произведение объясняющей переменной X1 и фиктивной переменной Х2. Если этот вклад является статистически значимым, исходную модель регрессии применять нельзя. Результаты регрессионного анализа, включающего переменные Х1, Х2 и Х3 = Х1*Х2 приведены на рис. 13.
Рис. 13. Результаты, полученные с помощью Пакета анализа Excel для регрессионной модели, учитывающей жилую площадь, наличие камина и их взаимодействие
Для того чтобы проверить нулевую гипотезу Н0: β3 = 0 и альтернативную гипотезу Н1: β3 ≠ 0, используя результаты, приведенные на рис. 13, обратим внимание на то, что t-статистика, соответствующая эффекту взаимодействия переменных, равна 1,48. Поскольку р-значение равно 0,166 > 0,05, нулевая гипотеза не отклоняется. Следовательно, взаимодействие переменных не имеет существенного влияния на модель регрессии, учитывающую жилую площадь и наличие камина.
Резюме. В заметке показано, как менеджер по маркетингу может применять множественный линейный анализ для предсказания объема продаж, зависящего от цены и затрат на рекламу. Рассмотрены различные модели множественной регрессии, включая квадратичные модели, модели с фиктивными переменными и модели с эффектами взаимодействия (рис. 14).
Рис. 14. Структурная схема заметки
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 873–936
🌟 Видео
Решение уравнения методом замены переменнойСкачать

Линейное уравнение с двумя переменными. 7 класс.Скачать

Алгебра 7 Линейное уравнение с одной переменнойСкачать

Алгебра Система уравнений Метод замены переменной № 6.22 9 классСкачать

Решение биквадратных уравнений. 8 класс.Скачать

7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

Линейные уравнения с одной переменной, содержащие переменную под знаком модуля. 6 класс.Скачать

Линейное уравнение с одной переменнойСкачать

Задание 9 на ОГЭ по математике 2023 / Разбираем все типы уравнений за 5 минут!Скачать

Линейное уравнение с одной переменной. Практическая часть. 6 класс.Скачать

Переменные и уравнения. ВведениеСкачать

Линейное уравнение с одной переменнойСкачать

решение уравнения с заменой переменнойСкачать
РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

Решение систем уравнений методом подстановкиСкачать

Уравнение с двумя переменными и его график. Алгебра, 9 классСкачать

1203.Метод разделения переменныхСкачать

ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать

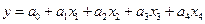 ).
).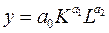 означает, что объем выпуска продукции (Y), является функцией количества капитала ( K ) и количества (L) труда).
означает, что объем выпуска продукции (Y), является функцией количества капитала ( K ) и количества (L) труда).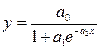 , где Y —удельная величина спроса, Х — среднедушевой доход).
, где Y —удельная величина спроса, Х — среднедушевой доход).