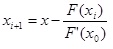Цель: дать представление о нелинейных уравнениях с двумя переменными.
Планируемые результаты: научиться решать простейшие нелинейные уравнения с двумя переменными.
Тип урока: урок общеметодологической направленности.
I. Сообщение темы и цели урока
II. Работа по теме урока
В курсе алгебры, помимо линейных уравнений с двумя переменными, рассматриваются и нелинейные уравнения с двумя переменными. К таким уравнениям относят те, в которых хотя бы одна из переменных входит в степени выше первой. Уравнения, содержащие знаки модуля, также будем относить к нелинейным уравнениям.
Нелинейным является уравнение:
а) 2х + |у — 1| = 3, так как содержит модуль величины у — 1;
б) х 2 + 3х — 7у = 1, так как содержит квадрат величины х;
в) х + у — ху = 5, так как содержит произведение ху — одночлен второй степени.
Количество решений нелинейного уравнения с двумя переменными может быть различным.
Рассмотрим уравнение 2(х — 1) 2 + 3(у + 2) 2 = -5. Очевидно, что при любых значениях переменных х и у квадраты величин х — 1 и у + 2 будут неотрицательными. При умножении их на положительные числа 2 и 3 произведения также неотрицательные. Сумма таких неотрицательных величин тоже неотрицательна. Поэтому левая часть данного уравнения при всех значениях переменных х и у неотрицательна и не может равняться отрицательному числу -5, стоящему в правой части. Следовательно, это уравнение решений не имеет.
Рассмотрим уравнение |2х — 3| + |4у — 5| = 0. В соответствии со свойством модуля величины он имеет только неотрицательные значения. Сумма двух неотрицательных выражений также неотрицательна и будет равняться нулю, если каждое из них равно нулю. Получаем уравнения |2х — 3| = 0 и |4у — 5| = 0.
Если модуль величины равен нулю, то и сама величина равна нулю. Получаем два линейных уравнения 2х — 3 = 0 (откуда х = 3/2) и 4у — 5 = 0 (откуда у = 5/4). Итак, данное уравнение имеет единственное решение
Рассмотрим уравнение х 4 — 2х 2 + |у — 2| + 1 = 0. Выделим квадрат разности и получим (х 4 — 2х 2 + 1) + |у — 2| = 0 или (х 2 — 1) 2 + |у — 2| = 0. Выражения (х 2 — 1) 2 и |у — 2| неотрицательны. Сумма этих неотрицательных величин будет равняться нулю, если каждое из них равно нулю. Получаем уравнения (х 2 — 1) 2 = 0 и |у — 2| = 0 или х 2 — 1 = 0 и у – 2 = 0 (откуда у = 2).
Для решения первого уравнения разложим его левую часть на множители, используя формулу разности квадратов: (х — 1)(х + 1) = 0. Произведение множителей равно нулю, если хотя бы один из них равен нулю, т. е. х — 1 = 0 (откуда х = 1) и х + 1 = 0 (тогда х = -1). Таким образом, данное уравнение имеет два решения: (1; 2) и (-1; 2).
Рассмотрим уравнение 3у + 2х 2 = 5. Выразим из него неизвестное у и получим 3у = 5 — 2х 2 или
Очевидно, что для любого выбранного значения х по этой формуле можно найти значение у. Например:
при х = 1 получаем
при х = 2 получаем и т. д.
Итак, мы нашли решения (1; 1), (2; -1). Очевидно, что данное уравнение имеет бесконечно много решений.
Достаточно часто встречаются нелинейные уравнения с параметрами.
При каком значении параметра а уравнение 3ах 2 + 2у 3 + ах + ау = 17 имеет решение (2; 1)?
Так как решение данного уравнения известно, то при его подстановке в уравнение получаем верное равенство 3а ∙ 2 2 + 2 ∙ 1 3 + а ∙ 2 + а ∙ 1 = 17 или 12а + 2 + 2а + а = 17.
Приведем подобные члены и получим 15а + 2 = 17, или 15а = 17 — 2, или 15а = 15, откуда а = 1.
Определим значение параметра а, при котором уравнение 3х 2 + х — 4у + 6 = 0 имеет решение (а — 1; а + 2), и найдем это решение.
Подставим заданное решение в данное уравнение и получим верное равенство 3(а — 1) 2 + (а — 1) — 4(а + 2) + 6 = 0, или 3а 2 — 6а + 3 + а — 1 — 4а — 8 + 6 = 0, или 3а 2 — 9а = 0.
Разложим левую часть уравнения на множители: 3а(а — 3) = 0. Произведение множителей равно нулю, если хотя бы один из них равен нулю, т. е. а = 0 или а — 3 = 0 (тогда а = 3). Для каждого из двух найденных значений а определим решение данного уравнения, подставив а в решение (а — 1; а + 2). При а = 0 получаем (-1; 2), при а = 3 получаем (2; 5).
При каком значении параметра а решением уравнения 2ах 2 — 3х 2 -9у + бау + 6х — 4ах = 0 будет любая пара чисел? Задачу можно решить двумя способами.
По условию решением данного уравнения будет любая пара чисел. Пусть этим решением будет, например, пара чисел (1; 1). Подставим эти числа в уравнение и получим 2а ∙ 1 2 — 3 ∙ 1 2 — 9 ∙ 1 + 6а ∙ 1 + 6 ∙ 1 — 4а ∙ 1 = 0, или 2а — 3 — 9 + 6а + 6 — 4а = 0, или 4а — 6 = 0, откуда а = 1,5.
Подставим это значение в уравнение и получим 2 ∙ 1,5х 2 — 3х 2 — 9у + 6 ∙ 1,5у + 6х — 4 ∙ 1,5 ∙ х = 0 или 0 ∙ х 2 + 0 ∙ у + 0 ∙ х = 0.
Очевидно, что любые числа х и у являются решением этого уравнения.
Сгруппируем члены данного уравнения и вынесем общий множитель за скобки. Получаем (2ах 2 + бау — 4ах) + (-3х 2 -9у + 6х) = 0, или 2а(х 2 + 3у — 2х) — 3(х 2 + 3у — 2х) — 0, или (х 2 + 3у — 2х)(2а — 3) = 0.
Очевидно, что это произведение будет равно нулю при всех значениях х и у, если второй множитель равен нулю, т. е. 2а — 3 = 0, откуда а = 1,5.
III. Задания на уроке и на дом
1. Решите уравнение с двумя неизвестными:
2. Определите значение параметра а, при котором данное уравнение имеет заданное решение. Найдите это решение.
3. Найдите значение параметра а, при котором данное уравнение имеет заданное решение:
4. Найдите значение параметра а, при котором решением данного уравнения будет любая пара чисел:
IV. Контрольные вопросы
— Какое уравнение называется нелинейным? Приведите примеры.
— Что называется решением нелинейного уравнения с двумя переменными?
— Сколько решений может иметь нелинейное уравнение с двумя переменными?
V. Подведение итогов урока
Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.
Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.
Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.
Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.
© 2014-2022 Все права на дизайн сайта принадлежат С.Є.А.
Видео:Линейное уравнение с двумя переменными. 7 класс.Скачать
Разница между линейным уравнением и нелинейным уравнением
Разница между линейным уравнением и нелинейным уравнением — Наука
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать
Содержание:
Линейное уравнение против нелинейного уравнения
В математике алгебраические уравнения — это уравнения, которые составлены с использованием полиномов. В явном виде уравнения будут иметь вид P (Икс) = 0, где Икс вектор из n неизвестных переменных, а P — многочлен. Например, P (x, y) = 4x 5 + ху 3 + y + 10 = 0 — алгебраическое уравнение с двумя переменными, записанное явно. Также (x + y) 3 = 3x 2 у — 3zy 4 является алгебраическим уравнением, но в неявной форме и примет вид Q (x, y, z) = x 3 + y 3 + 3xy 2 + 3zy 4 = 0, когда-то написано явно.
Важной характеристикой алгебраического уравнения является его степень. Он определяется как наивысшая степень членов уравнения. Если терм состоит из двух или более переменных, сумма показателей каждой переменной будет считаться мощностью члена. Заметим, что согласно этому определению P (x, y) = 0 имеет степень 5, а Q (x, y, z) = 0 — степень 5.
Линейные уравнения и нелинейные уравнения представляют собой два раздела, определенные на системе алгебраических уравнений. Степень уравнения — это фактор, который отличает их друг от друга.
Что такое линейное уравнение?
Линейное уравнение — это алгебраическое уравнение степени 1. Например, 4x + 5 = 0 — это линейное уравнение одной переменной. x + y + 5z = 0 и 4x = 3w + 5y + 7z — линейные уравнения с 3 и 4 переменными соответственно. В общем случае линейное уравнение от n переменных будет иметь вид m1Икс1 + м2Икс2 +… + Мп-1Иксп-1 + мпИксп = б. Здесь xяS — неизвестные переменные, mяS и b — действительные числа, где каждое из mя не равно нулю.
Такое уравнение представляет собой гиперплоскость в n-мерном евклидовом пространстве. В частности, линейное уравнение с двумя переменными представляет собой прямую линию в декартовой плоскости, а линейное уравнение с тремя переменными представляет собой плоскость в трехмерном евклидовом пространстве.
Что такое нелинейное уравнение?
Квадратное уравнение — это алгебраическое уравнение, которое не является линейным. Другими словами, нелинейное уравнение — это алгебраическое уравнение степени 2 или выше. Икс 2 + 3x + 2 = 0 — нелинейное уравнение с одной переменной. Икс 2 + y 3 + 3xy = 4 и 8yzx 2 + y 2 + 2z 2 + x + y + z = 4 — примеры нелинейных уравнений от 3 и 4 переменных соответственно.
Нелинейное уравнение второй степени называется квадратным уравнением. Если степень равна 3, то это называется кубическим уравнением. Уравнения степени 4 и степени 5 называются уравнениями четвертой и пятой степени соответственно. Было доказано, что не существует аналитического метода для решения любого нелинейного уравнения степени 5, и это верно и для любой более высокой степени. Решаемые нелинейные уравнения представляют собой гиперповерхности, которые не являются гиперплоскостями.
В чем разница между линейным уравнением и нелинейным уравнением?
• Линейное уравнение — это алгебраическое уравнение степени 1, а нелинейное уравнение — это алгебраическое уравнение степени 2 или выше.
• Несмотря на то, что любое линейное уравнение разрешимо аналитически, в нелинейных уравнениях это не так.
• В n-мерном евклидовом пространстве пространство решений линейного уравнения с n переменными является гиперплоскостью, а пространство решений нелинейного уравнения с n переменными — гиперповерхностью, которая не является гиперплоскостью. (Квадрики, кубические поверхности и др.)
Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать
Решение нелинейных уравнений
Уравнения, в которых содержатся неизвестные функции, произведенные в степень больше единицы, называются нелинейными.
Например, y=ax+b – линейное уравнение, х^3 – 0,2x^2 + 0,5x + 1,5 = 0 – нелинейное (в общем виде записывается как F(x)=0).
Системой нелинейных уравнений считается одновременное решение нескольких нелинейных уравнений с одной или несколькими переменными.
Существует множество методов решения нелинейных уравнений и систем нелинейных уравнений, которые принято относить в 3 группы: численные, графические и аналитические. Аналитические методы позволяют определить точные значения решения уравнений. Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений. Численное решение нелинейных уравнений предполагает прохождения двух этапов: отделение корня и его уточнение до определенно заданной точности.
Отделение корней осуществляется различными способами: графически, при помощи различных специализированных компьютерных программ и др.
Рассмотрим несколько методов уточнения корней с определенно заданной точностью.
Методы численного решения нелинейных уравнений
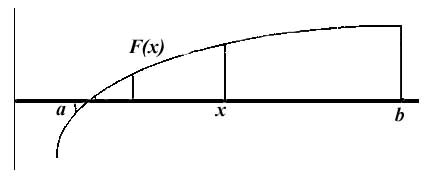
Метод половинного деления.
Суть метода половинного деления заключается в делении интервала [a,b] пополам (с=(a+b)/2) и отбрасывании той части интервала, в которой отсутствует корень, т.е. условие F(a)xF(b) 
Рис.1. Использование метода половинного деления при решении нелинейных уравнений.
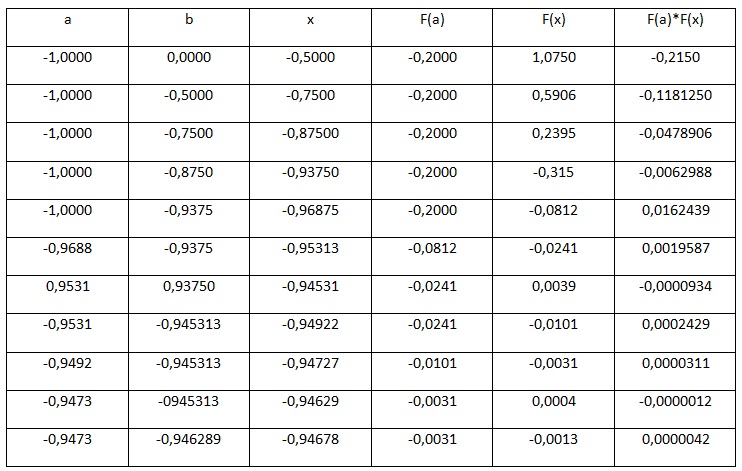
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0, то начала отрезка a переносится в x (a=x), иначе, конец отрезка b переносится в точку x (b=x). Полученный отрезок делим опять пополам и т.д. Весь произведенный расчет отражен ниже в таблице.
Рис.2. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
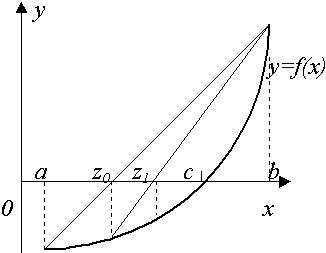
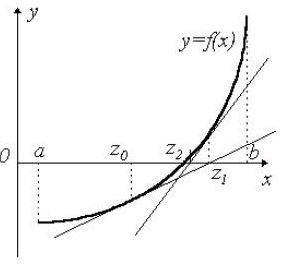
При использовании метода хорд, задается отрезок [a,b], в котором есть только один корень с установленной точностью e. Через точки в отрезке a и b, которые имеют координаты (x(F(a);y(F(b)), проводится линия (хорда). Далее определяются точки пересечения этой линии с осью абсцисс (точка z).
Если F(a)xF(z) 
Рис.3. Использование метода хорд при решении нелинейных уравнений.
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0;
Определим вторую производную F’’(x) = 6x-0,4.
F’’(-1)=-6,4 0 соблюдается, поэтому для определения корня уравнения воспользуемся формулой:
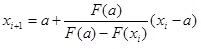
, где x0=b, F(a)=F(-1)=-0,2
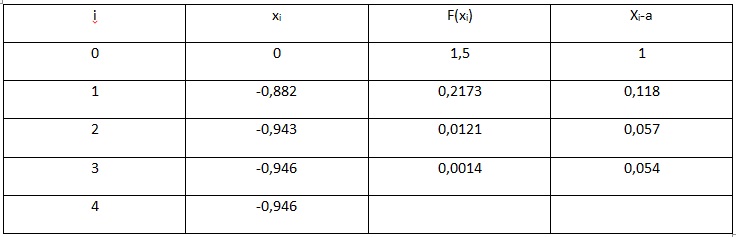
Весь произведенный расчет отражен ниже в таблице.
Рис.4. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
Метод касательных (Ньютона)
Данный метод основывается на построении касательных к графику, которые проводятся на одном из концов интервала [a,b]. В точке пересечения с осью X (z1) строится новая касательная. Данная процедура продолжается до тех пор, пока полученное значение не будет сравним с нужным параметром точности e (F(zi) 
Рис.5. Использование метода касательных (Ньютона) при решении нелинейных уравнений.
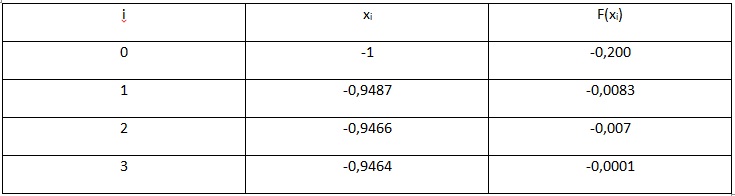
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0 выполняется, поэтому расчеты производим по формуле:
Весь произведенный расчет отражен ниже в таблице.
Рис.6. Таблица результатов вычислений
В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
📽️ Видео
ЛИНЕЙНОЕ УРАНЕНИЕ С ДВУМЯ ПЕРЕМЕННЫМИ — Как решать линейное уравнение // Алгебра 7 классСкачать
Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать
Нелинейные уравнения с двумя переменными и их геометрический смысл. 9 класс.Скачать
Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать
Как решать уравнения? уравнение 7 класс. Линейное уравнениеСкачать
Алгебра 7 Линейное уравнение с одной переменнойСкачать
Способы решения систем нелинейных уравнений. 9 класс.Скачать
Алгебра 7 класс. 11 сентября. Решение линейных уравнений #1Скачать
Решение системы линейных уравнений с двумя переменными способом подстановки. 6 класс.Скачать
После этого видео, ТЫ РЕШИШЬ ЛЮБУЮ Систему Нелинейных УравненийСкачать
7 класс, 39 урок, Метод алгебраического сложенияСкачать
Алгебра 7 класс (Урок№47 - Равносильность уравнений и систем уравнений.)Скачать
Урок по теме СПОСОБ ПОДСТАНОВКИ 7 классСкачать
Как решить уравнение #россия #сша #америка #уравненияСкачать
Решение систем уравнений методом подстановкиСкачать
Способы решения систем нелинейных уравнений. Практическая часть. 9 класс.Скачать
Видеоурок. 7 класс. Решение линейных уравнений с одним неизвестнымСкачать
