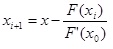Что такое нелинейное уравнение с одной переменной (8 видео)

Решение нелинейных уравнений с одной переменной

Раздел 2. Численные методы

Содержание

Тема 1. Решение нелинейных уравнений с одной переменной
Решение нелинейных уравнений
Методы численного решения нелинейных уравнений
Численное решение нелинейных уравнений с одной переменной
Учащимся 10-11 классов
доцент кафедры информатики и информационных технологий ГОУ ВПО ДВГГУ
Численное решение нелинейных уравнений с одной переменной
💡 Видео

Тема 1. Решение нелинейных уравнений с одной переменной

При решении ряда задач физики, механики и техники возникает необходимость решения уравнений с одной переменной. В общем случае нелинейное уравнение можно записать в виде: F(x)=0, где функция F(x) определена и непрерывна на промежутке . Корнем уравнения F(x)=0, является такое число c из области определения функции y=F(x), для которого справедливо равенство F(c)=0.

Поскольку подавляющее большинство нелинейных уравнений не решается путем аналитических преобразований (точными методами), на практике их решают численными методами. Решить такое уравнение численными методами значит установить, имеет ли оно корни, сколько корней, и найти все его корни с заданной точностью.

Задача численного решения уравнений состоит из двух этапов:

1. Отделение корней, т. е. нахождение достаточно малых окрестностей рассматриваемой области, в которых содержится единственный корень.

2. Уточнение корней, т. е. вычисление корней с заданной степенью точности в некоторой окрестности.

Во многих случаях отделение корней можно произвести графически. Для этого необходимо построить график функции y=F(x) и найти достаточно малые отрезки, содержащие по одной точке пересечения графика с осью ОХ. Иногда построение значительно упрощается, если функцию y=F(x) представить в виде f₁ (x)=f₂ (x) и найти отрезки оси ОХ, содержащие координаты х точек пересечения.

Отделение корней можно также произвести с помощью соответствующей компьютерной программы.

Пусть имеется уравнение F(x)=0, причем все интересующие вычислителя корни находятся на отрезке [A, B], на котором функция определена и непрерывна. Требуется отделить корни уравнения, т.е. найти отрезки [a, b] [A, B], содержащие по одному корню. Очевидно, что если на отрезке [a, b] функция меняет знак, то на этом отрезке находится, по крайней мере, один корень уравнения F(x)=0. Если длина отрезка [a, b] очень мала и F(a)*F(b) 0

Выбирая в каждом случае тот из отрезков, на котором функция меняет знак, и продолжая процесс половинного деления дальше, можно дойти до сколь угодно малого отрезка, содержащего корень уравнения.

Данный метод позволяет находить корни уравнения с заданной точностью е. Действительно, если на каком-то этапе процесса деления получен отрезок [a’, b’], содержащий корень, то приняв x≈(a’+b’)/2, мы найдем корень с точностью е (b’-a’)/2.

1.4. Уточнение корней методом итерации

Заменим уравнение F(x)=0 равносильным уравнением x=f(x). Пусть x* — искомый корень уравнения, а x₀ – полученное каким-либо способом грубо приближенное значение корня. Подставим x₀ в правую часть уравнения x=f(x), получим x₁ =f(x₀ ). Продолжая процесс подстановки, получим последовательность чисел: x₂ =f(x₁ ), x₃ =f(x₂ ),…, x_n =f(x_n-1 ). Такая последовательность называется последовательностью приближений или итерационной последовательностью.

Достаточное условие сходимости итерационного процесса

Пусть на отрезке [ a, b] уравнение x= f( x) имеет единственный корень и выполняются условия:

2. [ a, b] для всех х из [ a, b];

3. Существует такое действительное число q, что , для всех х из [ a, b];

Тогда итерационная последовательность x_n = f( x_n-1 ) сходится при любом начальном значении x₀ [ a, b].

Это условие не является необходимым, т.е. итерационная последовательность может сходиться и в том случае, если условия теоремы не выполняются.

Оценка погрешности метода итерации

Пусть , тогда или . Это значит, что процесс итерации надо продолжать до тех пор, пока модуль разности двух соседних приближений не станет меньше .

1.5. Уточнение корней методом хорд

Пусть уравнение F(x)=0 имеет единственный корень на отрезке [a, b]. Если отрезок [a, b] достаточно мал, то можно считать, что функция y=F(x) монотонна на этом отрезке и не меняет направление выпуклости. Значит на отрезке [a, b] нет точек максимума и минимума, т.е. . Т.к. направление выпуклости не меняется то и . Получаем четыре вида графиков, которые объединяются в два типа.

I. тип. Условие: , где x- любая точка [a, b].

Что такое нелинейное уравнение с одной переменной

II. тип. Условие: , где x- любая точка [a, b].

Пусть x* — искомый корень уравнения F(x)=0. Заменим кривую графика на хорду АВ. Уравнение прямой, проходящей через точки А (а, F(а)) и В(b, F(b)) имеет вид: , где (x, y) – любая точка прямой АВ. В качестве этой точки возмем точку пересечения хорды с осью ОХ, т.е.

(x₁ , 0). Получим или .

Рассмотрим случай, когда кривая графика функции y= F( x) относится к I типу. Через точки А₁ и В проводим следующую хорду. Она пересекает ось ОХ в точке х_2. Аналогично получаем

(1)

Полученная таким образом формула (1) называется формулой метода хорд для кривых I-го типа.

Очевидно, что последовательность значений х₁ , х₂ , х₃ , …,х_n стремится к корню уравнения х * , а значит этот корень можно найти с заданной точностью.

В рассмотренном выше случае для кривых I-го типа, правым концом всех проведенных хорд была точка В. Если, кривая относится ко II-му типу, то неизменным концом хорд будет точка А. Значит в формуле (1) b поменяется на а. Формула будет иметь вид:

Если на n-ом шаге , то считается, что необходимая точность е достигнута.

1.6. Уточнение корней методом касательных

При уточнении корней методом касательных все функции делятся на два типа, как и в методе хорд. Рассмотрим кривую I-го типа.

Проведем касательную к графику функции в точке В. Она пересечет ось ОХ в точке х_1. Через эту точку проведем прямую перпендикулярную оси ОХ до пересечения с графиком функции. Получим точку А₁ . Через неё опять проведем касательную. Получим точку х₂ . Продолжая этот процесс, получим последовательность х₁ , х₂ , х₃ , …,х_n, сходящуюся к х * .

Уравнение касательной к графику функции F(x)=0 в точке х=b имеет вид . Т.к. эта касательная пересекает ось ОХ в точке (х₁ , 0), то . Значит

Если, кривая относится ко II-му типу, то первую касательную к графику функции надо проводить в точке А и

Дальнейший расчет значений х₂ , х₃ , …,х_n не зависит от типа кривой и в обоих случаях вычисляется по формуле

Если на n-ом шаге , то считается, что необходимая точность е достигнута.

1.7. Уточнение корней комбинированным методом хорд и касательных

Методы хорд и касательных дают приближение корня с разных сторон. Поэтому их часто применяют в сочетании друг с другом. В этом случае процесс уточнения корня идет быстрее.

Метод реализуется по следующей схеме:

1. По методу хорд находят первое приближение корня .

2. По методу касательных находят . Если кривая относится к I-му типу, то . Если ко II-му типу, то .

3. По методу хорд .

4. По методу касательных .

Шаги 3 и 4 повторяются до тех пор, пока . Как только можно считать корень найденным .

Лабораторная работа №1. Решение нелинейных уравнений с одной переменной.

1. Сделать программу отделения корней уравнения F(x)=0 на [a, b] с шагом 0,5.

2. Сделать программы уточнения корней уравнения F(x)=0 на одном из отрезков, полученных в первой программе с точностью 0,001.

a) Методом половинного деления;

a) Методом итерации;

c) Методом касательных;

d) Комбинированным методом хорд и касательных.

Видео:Алгебра 7 Линейное уравнение с одной переменной Скачать

Решение нелинейных уравнений

Уравнения, в которых содержатся неизвестные функции, произведенные в степень больше единицы, называются нелинейными.
Например, y=ax+b – линейное уравнение, х^3 – 0,2x^2 + 0,5x + 1,5 = 0 – нелинейное (в общем виде записывается как F(x)=0).

Системой нелинейных уравнений считается одновременное решение нескольких нелинейных уравнений с одной или несколькими переменными.

Существует множество методов решения нелинейных уравнений и систем нелинейных уравнений, которые принято относить в 3 группы: численные, графические и аналитические. Аналитические методы позволяют определить точные значения решения уравнений. Графические методы наименее точны, но позволяют в сложных уравнениях определить наиболее приближенные значения, с которых в дальнейшем можно начинать находить более точные решения уравнений. Численное решение нелинейных уравнений предполагает прохождения двух этапов: отделение корня и его уточнение до определенно заданной точности.
Отделение корней осуществляется различными способами: графически, при помощи различных специализированных компьютерных программ и др.

Рассмотрим несколько методов уточнения корней с определенно заданной точностью.

Методы численного решения нелинейных уравнений

Метод половинного деления.

Суть метода половинного деления заключается в делении интервала [a,b] пополам (с=(a+b)/2) и отбрасывании той части интервала, в которой отсутствует корень, т.е. условие F(a)xF(b)

Рис.1. Использование метода половинного деления при решении нелинейных уравнений.

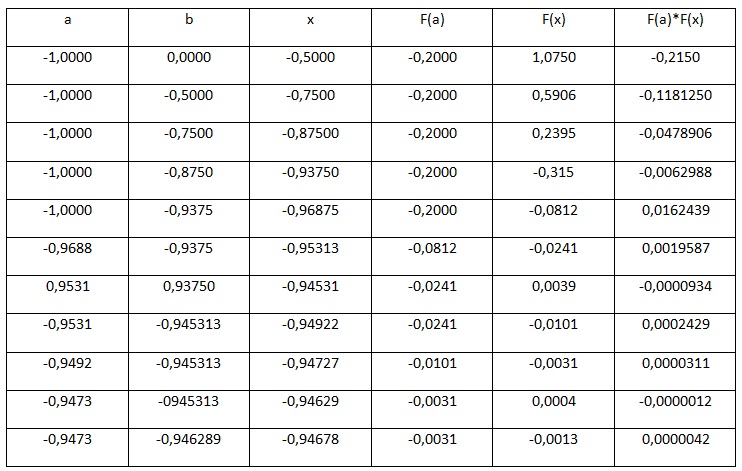
Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0, то начала отрезка a переносится в x (a=x), иначе, конец отрезка b переносится в точку x (b=x). Полученный отрезок делим опять пополам и т.д. Весь произведенный расчет отражен ниже в таблице.

Рис.2. Таблица результатов вычислений

В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946

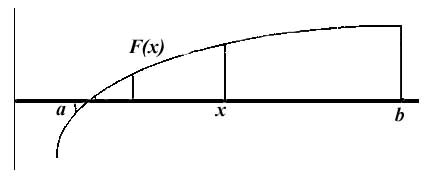
При использовании метода хорд, задается отрезок [a,b], в котором есть только один корень с установленной точностью e. Через точки в отрезке a и b, которые имеют координаты (x(F(a);y(F(b)), проводится линия (хорда). Далее определяются точки пересечения этой линии с осью абсцисс (точка z).
Если F(a)xF(z)

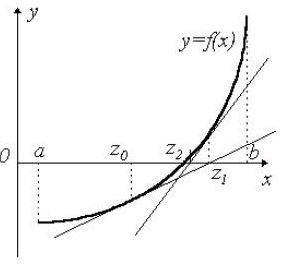
Рис.3. Использование метода хорд при решении нелинейных уравнений.

Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0;

Определим вторую производную F’’(x) = 6x-0,4.

F’’(-1)=-6,4 0 соблюдается, поэтому для определения корня уравнения воспользуемся формулой:

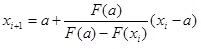
, где x0=b, F(a)=F(-1)=-0,2

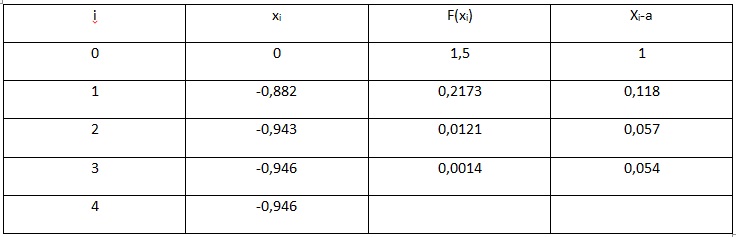
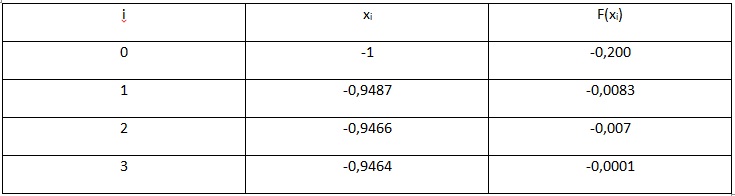
Весь произведенный расчет отражен ниже в таблице.

Рис.4. Таблица результатов вычислений

В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946

Метод касательных (Ньютона)

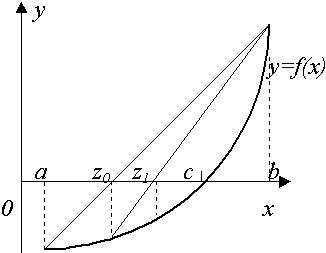
Данный метод основывается на построении касательных к графику, которые проводятся на одном из концов интервала [a,b]. В точке пересечения с осью X (z1) строится новая касательная. Данная процедура продолжается до тех пор, пока полученное значение не будет сравним с нужным параметром точности e (F(zi)

Рис.5. Использование метода касательных (Ньютона) при решении нелинейных уравнений.

Рассмотрим пример. Необходимо решить уравнение х^3 – 0,2x^2 + 0,5x + 1,5 = 0 с точностью до e 0 выполняется, поэтому расчеты производим по формуле:

Весь произведенный расчет отражен ниже в таблице.

Рис.6. Таблица результатов вычислений

В результате вычислений получаем значение с учетом требуемой точности, равной x=-0,946

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Численное решение нелинейных уравнений с одной переменной

Видео:Урок 7 ЛИНЕЙНОЕ УРАВНЕНИЕ С ОДНОЙ ПЕРЕМЕННОЙСкачать

Учащимся 10-11 классов

Видео:7 класс, 4 урок, Линейное уравнение с одной переменнойСкачать

доцент кафедры информатики и информационных технологий ГОУ ВПО ДВГГУ

Видео:Линейное уравнение с одной переменнойСкачать

Численное решение нелинейных уравнений с одной переменной

При решении задач прикладного характера в разнообразных разделах физики, механики, техники и других областях возникает необходимость решения нелинейных уравнений с одной переменной. При этом многие уравнения не имеют аналитических решений. Это относится к большинству трансцендентных уравнений. Также доказано, что нельзя построить формулу, по которой можно было бы решить произвольное алгебраические уравнение выше четвертой степени.

Уравнение будем называть линейным[1], алгебраическим или трансцендентным в зависимости от того, имеет ли оно одно решение, n решений или неопределенное число решений.

Нелинейные уравнения можно разделить на два класса – алгебраические и трансцендентные. Алгебраическими уравнениями называют уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). Например, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и другие) называются трансцендентными.[2]

Методы решения нелинейных уравнений делятся на две группы:

Точные методы позволяют записать корни в виде некоторого конечного соотношения (формулы). Из школьного курса алгебры известны такие методы для решения тригонометрических, логарифмических, показательных, а также простейших алгебраических уравнений.

Если алгебраическое или трансцендентное уравнение достаточно сложное, то его корни сравнительно редко удается найти точно. Поэтому большое значение приобретают способы приближенного нахождения корней уравнения и оценки степени их точности. Если точно определить корни уравнения не представляется возможным, для их решения используют численные итерационные (iteration — повторение) методы с заданной степенью точности.

Далее будут рассмотрены несколько численных методов и приведены алгоритмы нахождения корней уравнений.

В общем случае нелинейное уравнение можно записать в виде:

(1)

где функция F(x) — определена и непрерывна на некотором конечном или бесконечном интервале

(2)

где функции f(x) и g(x) также определены и непрерывны на интервале .

Всякое число обращающее уравнения (1) или (2) в верные числовые равенства называется корнем этого уравнения.

Корни уравнения могут быть действительными и комплексными. В дальнейшем будет идти речь только о вычислении действительных корней.

Решить уравнение численно значит:

1) установить имеет ли оно действительные корни;

2) отделить эти корни (то есть на числовой оси найти достаточно тесные промежутки, называемые интервалами изоляции корня[3], содержащие только один корень данного уравнения);

3) уточнить отделенные корни, т. е. найти значения корней с заданной степенью точности .

Последнее означает следующее.

Пусть x* — точный корень уравнения и x* , то есть x* . Если , тогда числа и могут рассматриваться как приближенные значения корня x* соответственно с недостатком и с избытком с точностью до , так как и .

Любое число, содержащееся между и , можно принять за приближенное значение корня x* с точностью до .

Графические методы решения уравнений[4]

Пусть дано уравнение F (х) = 0. Построим график функции F (х). Абсциссы точек пересечения графика с осью Ох и являются корнями уравнения.

Иногда для графического решения уравнения удобнее записать его в виде и построить графики функций: и Абсциссы точек пересечения этих графиков и являются корнями уравнения F (х) = 0 (рис. 1).

Однако этот метод позволяет получить лишь грубо приближенные значения корней уравнения. Для получения значений корней с большей точностью применяются численные методы. Однако, графический метод очень удобен, так как он позволяет найти корни с точностью, достаточной для решения многих практических задач, а также достаточно нагляден, прост и доступен.

Численные методы решения уравнений

Наиболее распространенными на практике численными методами решения уравнения (1) являются: метод половинного деления, метод хорд, метод касательных, метод простой итерации и т. д.[5]

Процесс численного решения уравнений разбивается на три этапа:

1. Отделение корней уравнения. Этот процесс можно сделать как графически, так и аналитически. Важно найти такие отрезки, которые бы содержали по одному корню уравнения (1).

2. Выбор метода решения и преобразование уравнения к виду, удобному для применения данного метода.

3. Уточнение корней с заданной точностью при помощи выбранного численного метода.

Говорят, что корень x* уравнения отделен на отрезке , если он содержится в данном отрезке, и если на этом отрезке других корней нет.

Провести полное отделение всех корней уравнения – значит разбить всю область допустимых значений на интервалы (или на отрезки), в каждом из которых содержится ровно по одному корню (или не содержится ни одного корня).

Отделение корней обычно начинают проводить графически. Для этого строят графики функций, получают интервалы, в которых находятся корни уравнения. Это предположение затем проверяют аналитически, пользуясь следующим свойством непрерывной функции F(x): если функция непрерывна на интервале и на его концах имеет разные знаки (), то между точками a и b имеется хотя бы один корень уравнения .

При этом корней может оказаться и несколько, как показано на рис. 2. Рис.2

Для того, чтобы на интервале существовал только один корень, должно выполняться следующее свойство: если функция непрерывна и монотонна на отрезке и принимает на концах отрезка значения разных знаков, то внутри отрезка содержится корень уравнения и этот корень единственный (рис. 3, а, b).

Пример 1: Отделить графически положительные корни уравнения

Решение: Найдем приближенные значения корней уравнения графически. Для этого удобно представить уравнение в следующем виде: e0,3x = 2 sin(2x).

Решением данного уравнения будет являться абсцисса x точки пересечения графиков следующих функций:

На рисунке видно, что графики функций y1(x) и y2(x) пересекаются в двух точках A и B, абсциссы которых положительны и лежат соответственно в промежутках и. Следовательно, уравнение имеет два положительных корня x1 и x2, которые лежат в промежутках и.

Примечание: Графики функций можно строить с помощью компьютера, например, в электронных таблицах Excel или в свободно распространяемой системе компьютерной математики Scilab.[7]

Пример 2: Отделить аналитически корни уравнения

Решение: Для аналитического отделения корней найдем производную функции

Производная этой функции

ни в одной точке не обращается в нуль, т. к. D = 36 -4*3*11 0, следовательно, функция f везде возрастает, и уравнение (4) может иметь один корень.

[3] Методы определения интервала изоляции корня основаны на следующем свойстве: если непрерывная функция f(x) на интервале [a, b] поменяла знак, т. е. f(a)*f(b)