Что такое начальные и граничные условия при решении дифференциальных уравнений

Приведенные уравнения (10)-(12) являются частными случаями общего дифференциального уравнения с частными производными второго порядка. Эти уравнения описывают различные физические явления и процессы. Так уравнение гиперболического вида

описывает процессы, связанные с механическими, электрическими, акустическими и другими видами колебаний. Поэтому это уравнение называют волновым уравнением. В этом уравнении независимые переменные t и x характеризуют временную и пространственную координаты.

Уравнение параболического вида

описывает процессы тепло- и массопереноса, диффузию и другие процессы переноса. В случае изучения процесса теплопереноса его называют уравнением теплопроводности.

Уравнение эллиптического вида

,

называемое уравнением Пуассона, описывает стационарные (установившиеся, т. е не зависящие от времени) процессы, например стационарное температурное поле, потенциальное течение жидкости т. п.

Как и любые дифференциальные уравнения, приведенные уравнения имеют бесконечное множество решений, которые отличаются произвольными функциями (решения обыкновенных дифференциальных уравнений различаются значениями констант). Поэтому для получения единственного решения задают дополнительные условия, которые принято называть условиями однозначности. Они могут содержать в себе информацию о геометрических и физических свойствах исследуемого объекта, его исходном состоянии, о характеристиках воздействия на него объектов внешней среды и т. п.

Задание условий однозначности позволяет выделить конкретный рассматриваемый объект, конкретный процесс из общей группы подобных объектов и процессов. Например, распространение теплоты в заготовке при ее обработке точением, шлифованием или при сварке и других видах обработки, сопровождающихся передачей тепловой энергии, будет описываться одним и тем же уравнением теплопроводности. Однако является очевидным, что при шлифовании или при сварке температура и ее изменение в одних и тех же точках заготовки будет разной и зависеть от многих причин, в частности, какой источник теплоты воздействует на заготовку, какая была температура в точках заготовки до начала обработки и других факторов.

В условиях однозначности выделяют начальные и граничные условия. Начальные условия отражают состояние объекта, процесса или явления на исходный (начальный) момент времени наблюдения t₀ в виде значения искомого решения во всех точках x, y рассматриваемой области объекта, например

или , (13)

где θ(x, y, t₀) – температура в точке x, y рассматриваемой области объекта в момент времени t₀. Обычно принимают t₀ = 0; f(x, y) – известная функция.

В отдельных задачах начальные условия могут содержать в себе также значения производных искомого решения по времени, например, скорость изменения температуры в момент времени t₀ или скорость перемещения рассматриваемого тела в точке x, y.

Граничные условия отражают взаимодействие исследуемого объекта с объектами внешней среды, которое имеет место на ограничивающих его поверхностях. С физической точки зрения это взаимодействие может быть выражено в виде приложения к той или иной части поверхности исследуемого объекта внешней нагрузки (сосредоточенных или распределенных сил), подведения или отводе теплоты и т. п.

Математически вид или признак взаимодействия описывается в форме констант, функциональных зависимостей и т. д., определяющих значения искомого решения на граничных поверхностях объекта, а также нормальных к граничным поверхностям производных искомого решения.

Условия однозначности совместно с дифференциальным уравнением позволяют математически полностью и однозначно отразить конкретный рассматриваемый процесс или явление.

В зависимости от того, какие условия однозначности заданы в математической постановке задачи выделяют три типа задач.

Задача первого типа – это задача Коши, в которой дифференциальное уравнение дополнено только начальными условиями, задающими состояние объекта, процесса или явления на исходный (начальный) момент времени наблюдения. Граничные условия в задаче Коши отсутствуют. Отсутствие граничных условий определено тем, что рассматривается либо неограниченное пространство, либо весьма малый начальный промежуток времени t, при котором влияние границ еще пренебрежимо мало.

Задача Коши формулируется при решении дифференциальных уравнений гиперболического и параболического видов.

Задача второго типа – это задача, в которой нет начальных условий, а заданы только граничные условия. Это условия, в свою очередь, подразделяются обычно на три вида (рода).

Граничным условием первого рода является условие, при котором в точках x, y на границе Г рассматриваемой области искомая функция u(x, y) принимает заданные значения, например

.

Граничным условием второго рода является условие, при котором в точках x, y рассматриваемой области производная по нормали n к граничной поверхности Г (нормальная производная) искомой функции u(x, y) принимает заданные значения, например

.

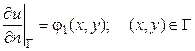
Граничным условием третьего рода является условие, при котором в точках x, y на границе Г рассматриваемой области задана линейная комбинация искомой функции и ее нормальной производной. Например, при решении задачи определения температурного поля в твердом теле это условие может иметь вид

,

где θ(x, y) – температура в точке x, y на границе Г поверхности рассматриваемого твердого тела; λ – коэффициент теплопроводности материала тела;

α – коэффициент теплоотдачи от поверхности тела; θ_о – температура окружающей среды.

В теплофизике технологических процессов механической обработки деталей часто используются граничные условия четвертого рода. Эти условия возникают тогда, когда рассматриваемое твердое тело находится в беззазорном контакте с другим твердым телом и между ними происходит теплообмен. При граничных условиях четвертого рода, когда контакт между телами идеален, температура в любой точке поверхности соприкосновения как со стороны одного, так ИСО стороны другого тела одна и та же, т. е.

.

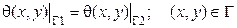
Задачи второго типа имеют место тогда, когда состояние объекта исследования рассматривается в моменты времени, достаточно удаленных от начального момента и влиянием начальных условий можно пренебречь. В этих случаях процесс, протекающий в объекте, считается установившимся, стационарным. Постановка задач этого типа может содержать дифференциальное уравнение любого типа.

Задача третьего типа – это так называемая смешанная задача, в которой задаются и начальные и граничные условия. Смешанная задача формулируется для гиперболических и параболических типов уравнений.

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Начальные и граничные условия

Здравствуйте, продолжаем нашу рубрику по дифференциальным уравнениям, это уже 2 статья, если вы хотите начать сначала и ознакомиться с видами дифференциальных уравнений, то вам в первую статью.

Введение

Итак, для использования численных методов при решении дифференциального уравнения необходимо дополнительные условия. Если искомая функция(концентрация, температура и т.д) является функцией времени u=u(t), то требуются начальные условия, которые являются значением этой функции в момент времени, принятый за начальный:

Если начальная функция также зависит и от пространственных координат u=u(t,x), то начальное условие характеризуют ее распределение в пространстве в начальный момент времени:

В последнем случае помимо начальных условий требуются еще и граничные условия, которые имеют значения функции u(t,x) на границе изучаемой системы для любого момента времени. Причем, если искомая функция зависит от нескольких пространственных координат, то необходимо задавать граничные условия по каждой из них.

Небольшой пример

Например для следующего уравнения:

• начальное условие
• 2 граничных условия по координате
• 1 граничное условие по координате
• 2 граничных условия по координате

Сразу же возникает вопрос, почему именно так? Так вот, порядок производной определяет количество граничных условий для переменной. Как вы заметили, по y присутствует только первая производная, поэтому и одно граничное условие.

Классификация граничных условий

Для лучшего понимания рассмотрим классификацию на примере уравнения:

будет изменятся от до , соответственно при , будет левая граница, а при , будет правая.

Граничные условия 1-ого рода

Записываются следующим образом:

— функции, зависящие от , как пример:

Граничные условия 2-ого рода

Здесь вместо самих функций используются их первые производные.

Граничные условия 3-ого рода

Смешанные граничные условия

В этом случае левое и правое граничные условия могут быть разных родов:

Заключение

На этом мы подходим к концу нашей статьи. Сегодня мы с вами изучили начальные и граничные условия в дифференциальных уравнениях. Если вам что то осталось непонятным, то это нормально, не пугайтесь. В будущих статьях мы будем еще подробнее разбираться с этими и другими тонкостями, ну а на сегодня это все.

Спасибо, что прочитали статью, если у вас остались вопросы, то задавайте их в комментариях.
И, буду вам очень признателен, если вы вступите в нашу группу вконтакте, ссылка на которую размещена слева вверху под названием сайта.

Видео:Дифференциальные уравнения. 11 класс.Скачать

Определения и понятия теории дифференциальных уравнений

С этой темы мы рекомендуем начинать изучение теории дифференциальных уравнений. В одном разделе мы собрали все основные термины и определения, которые будут применяться при рассмотрении теоретической части. Для того, чтобы облегчить усвоение материала, мы приводим многочисленные примеры.

Видео:Общее и частное решение дифференциального уравненияСкачать

Дифференциальное уравнение

Дифференциальное уравнение – это уравнение, которое содержит неизвестную функцию под знаком производной или дифференциала.

Обыкновенное дифференциальное уравнение содержит неизвестную функцию, которая является функцией одной переменной. Если же переменных несколько, то мы имеем дело с уравнением в частных производных.

Имеет значение также порядок дифференциального уравнения, за который принимают максимальный порядок производной неизвестной функции дифференциального уравнения.

Обыкновенные дифференциальные уравнения 1 -го, 2 -го и 5 -го порядков:

1 ) y ‘ + 1 = 0 ; 2 ) d 2 y d x 2 + y = x · sin x ; 3 ) y ( 5 ) + y ( 3 ) = a · y , α ∈ R

Уравнения в частных производных 2 -го порядка:

1 ) ∂ 2 u ∂ t 2 = v 2 · ∂ 2 u ∂ x 2 + ∂ 2 u ∂ y 2 + ∂ 2 u ∂ z 2 , u = u ( x , y , z , t ) , v ∈ R ; 2 ) ∂ 2 u ∂ x 2 — ∂ 2 u ∂ y 2 = 0 , u = u ( x , y )

С порядками ДУ разобрались. Далее мы будем в основном рассматривать обыкновенные дифференциальные уравнения n -ого порядка вида F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 или F x , y , d y d x , d 2 y d x 2 , . . . , d n y d x n = 0 , в которых Ф ( x , y ) = 0 — это заданная неявно функция. В тех случаях, когда это будет возможно, неявную функцию мы будем записывать в ее явном представлении y = f ( x ) .

Видео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Интегрирование дифференциального уравнения

Интегрирование дифференциального уравнения – это процесс решения этого уравнения.

Решением дифференциального уравнения является функция Ф ( x , y ) = 0 , которая задана неявно и которая обращает данное уравнение в тождество. В некоторых случаях нам нужно будет неявно заданную функцию у выражать через аргумент х явно.

Искать решение дифференциального уравнения мы всегда будем на интервале Х , который задается заранее.

В каких случаях мы будем учитывать интервал Х ? Обычно в условии задач он не упоминается. В этих случаях мы буде искать решение уравнения F ( x , y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) для всех х , при которых искомая функция у и исходное уравнение будут иметь смысл.

Интеграл дифференциального уравнения – это название решения дифференциального уравнения.

Функции y = ∫ x d x или y = x 2 2 + 1 можно назвать решением дифференциального уравнения y ‘ = x .

У одного дифференциального уравнения может быть множество решений.

Функция y = x 3 3 является решением ДУ y ‘ = x 2 . Если мы подставим полученную функцию в исходное выражение, то получим тождество y ‘ = x 3 3 = 1 3 · 3 x 2 = x 2 .

Вторым решением данного дифференциального уравнения является y = x 3 3 + 1 . Подстановка полученной функции в уравнение также превращает его в тождество.

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Общее решение ДУ

Общее решение ДУ – это все множество решений данного дифференциального уравнения.

Также общее решение часто носит название общего интеграла ДУ.

Общее решение дифференциального уравнения y ‘ = x 2 имеет вид y = ∫ x 2 d x или y = x 3 3 + C , где C – произвольная постоянная. Из общего интеграла ДУ y = x 3 3 + C мы можем прийти к двум решениям, которые мы привели в прошлом примере. Для этого нам нужно подставить значения С = 0 и C = 1 .

Видео:Работа с MathCad Prime. Решение дифференциальных уравнений.Скачать

Частное решение ДУ

Частное решение ДУ – это такое решение, которое удовлетворяет условиям, заданным изначально.

Для ДУ y ‘ = x 2 частным решением, которое будет удовлетворять условию y ( 1 ) = 1 , будет y = x 3 3 + 2 3 . Действительно, y ‘ = x 3 3 + 2 3 ‘ = x 2 и y ( 1 ) = 1 3 3 + 2 3 = 1 .

К числу основных задач из теории дифференциальных уравнений относятся:

• задачи Коши;
• задачи нахождения общего решения ДУ при заданном интервале Х ;
• краевые задачи.

Особенностью задач Коши является наличие начальных условий, которым должно удовлетворять полученное частное решение ДУ. Начальные условия задаются следующим образом:

f ( x 0 ) = f 0 ; f ‘ ( x 0 ) = f 1 ; f ‘ ‘ ( x 0 ) = f 2 ; . . . ; f ( n — 1 ) ( x 0 ) = f n — 1

где f 0 ; f 1 ; f 2 ; . . . ; f n — 1 — это некоторые числа.

Особенностью краевых задач является наличие дополнительных условий в граничных точках x 0 и x 1 , которым должно удовлетворять решение ДУ второго порядка: f ( x 0 ) = f 0 , f ( x 1 ) = f 1 , где f 0 и f 1 — заданные числа. Такие задачи также часто называют граничными задачами.

Линейное обыкновенное ДУ n -ого порядка имеет вид:

f n ( x ) · y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )

При этом коэффициенты f 0 ( x ) ; f 1 ( x ) ; f 2 ( x ) ; . . . ; f n ( x ) — это непрерывные функции аргумента х на интервале интегрирования.

Уравнение f n ( x ) · y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x ) будет называться линейным однородным дифференциальным уравнением в том случае, если f ( x ) ≡ 0 . Если нет, то мы будем иметь дело с линейным неоднородным ДУ.

В линейных однородных ДУ коэффициенты f 0 ( x ) = f 0 ; f 1 ( x ) = f 1 ; f 2 ( x ) = f 2 ; . . . ; f n ( x ) = f n могут быть постоянными функциями (некоторыми числами), то мы будем говорить о ЛОДУ с постоянными коэффициентами или ЛНДУ с постоянными коэффициентами. В ЛОДУ с постоянными коэффициентами f ( x ) ≡ 0 , в ЛНДУ с постоянными коэффициентами f ( x ) ненулевая.

Видео:Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами

Характеристическое уравнение ЛНДУ n -ой степени с постоянными коэффициентами – это уравнение n -ой степени вида f n · k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 .

Остальные определения мы будем разбирать в других темах по мере изучения теории.

🌟 Видео

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Дифференциальные уравнения: пример 5Скачать

Решение физических задач с помощью дифференциальных уравненийСкачать

Решение линейных дифференциальных уравненийСкачать

7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать

6.1 Решение ОДУ аппроксимация начальных условийСкачать

Линейное дифференциальное уравнение первого порядка (1-x^2)*y'-xy=1Скачать

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Простейшие дифференциальные уравненияСкачать

Задача Коши для дифференциальных уравненийСкачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать