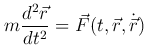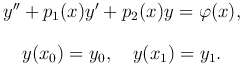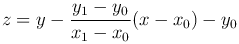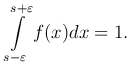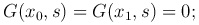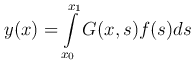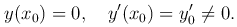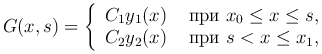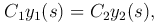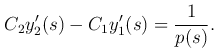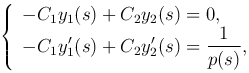Что такое краевые условия дифференциального уравнения

Видео:Задача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать

Лекция 4. Краевые задачи для дифференциальных уравнений. Задача Штурма-Лиувилля.

Будем рассматривать однородное линейное уравнение второго порядка

Ly ≡ a₂(x)y» + a₁(x)y’ + a₀(x)y = 0. Его можно записать по-другому:

(15)

Однородное уравнение Ly = 0 и неоднородное Ly = f, как известно, имеют бесконечное множество решений. На практике часто бывает нужно из множества решений выделить только одно. Для этого задают некоторые дополнительные условия. Если это начальные условия у(х₀) = у_o, y'(x_o) = y₁, то получают задачу Коши. Если задают дополнительные условия на концах некоторого отрезка, то получают задачу, которая называется краевой задачей. Условия, которые задаются на концах отрезка, называются краевыми условиями. Краевые условия иногда именуют также граничными условиями и тогда говорят о граничной задаче.
Мы будем задавать линейные краевые условия вида

(16)

где α₁, α₂, β₁, β₂, A, B — заданные числа, причем по крайней мере одно из чисел α₁, α₂, и одно из чисел β₁, β₂, отличны от нуля. Если в (16) хотя бы одно из чисел А и В не равно нулю, то краевые условия называют неоднородными. Если А = В = 0, то условия (16) называются однородными. Краевая задача называется однородной, если рассматривается однородное уравнение (15) Ly = 0 и однородные краевые условия (16). Решением краевой задачи называется такое решение дифференциального уравнения, которое удовлетворяет заданным краевым условиям. Заметим сразу, что однородная краевая задача всегда имеет решение у ≡ 0 (тривиальное решение).

Наряду с уравнением (15) рассмотрим уравнение

(17)

содержащее некоторый числовой параметр λ. Здесь функции р(х), q(x), r(x) действительные, а число λ может быть, вообще говоря, и комплексным. Краевая задача (17), (16) при А = В = 0 является однородной. Поэтому при любых λ она имеет тривиальное решение. Нас будут интересовать такие значения λ, при которых эта задача обладает не только тривиальными решениями.

Задача Штурма-Лиувилля. Найти те значения параметра λ, при которых уравнение (17) имеет нетривиальное решение, удовлетворяюшее однородным краевым условиям (16). В дальнейшем будем ее записывать в виде

<L_λy = 0, l₁y = 0, l₂y = 0>.
Те значения параметра λ, при которых задача Штурма-Лиувилля имеет ненулевое решение, называются собственными значениями (собственными числами) задачи, а сами эти решения — собственными функциями. Задачу Штурма-Лиувилля называют также задачей на собственные значения. В силу однородности уравнения и краевых условий собственные функции задачи Штурма-Лиувилля определены с точностью до постоянного множителя. Это означает, что если y(х) -собственная функция при некотором значении λ, то произведение Cy(x), где С — произвольная постоянная, также является собственной функцией при том же значении параметра λ. В связи с этим часто в качестве собственной функции рассматривают нормированную функцию у <х), у которой ||у(х)|| = 1. Такая собственная функция определена, по существу, однозначно (с точностью до знака ±). Далее мы подробно изучим наиболее простой случай задачи Штурма-Лиувилля, когда уравнение имеет вид

Из множества краевых условий вида (16) ограничимся тремя частными случаями:

1) краевые условия первого рода

2) краевые условия второго рода

3) краевые условия третьего рода

(21)

Общая задача Штурма-Лиувилля будет обладать свойствами, очень похожими на свойства в этих простых случаях, если на коэффициенты уравнения (17) наложить дополнительные условия: р(х), q(x), f(x) -непрерывные функции, причем р(х) имеет, кроме того, непрерывную производную на [а, b], р(х) > 0, q(x) ≥ 0.

Основные свойства собственных значений и собственных функций задачи Штурма-Лиувилля.

Лемма. Определитель Вронского двух собственных функций задачи Штурма-Лиувилля на концах отрезка [а, b] равен нулю.

Доказательство. Напомним, что определителем Вронского функций у = y₁(x) и у = у₂(x) называется определитель вида

Рассмотрим однородные краевые условия общего вида (16). Пусть у₁(x) и у₂(x) — две любые собственные функции. Это означает, что в точке x = а выполняются равенства

Числа α₁, и α₂ не могут одновременно равняться нулю. Значит, алгебраическая система двух однородных уравнений с двумя неизвестными имеет ненулевое решение. Это возможно только в том случае, когда определитель этой системы равен нулю:

Этот определитель совпадает с определителем Вронского в точке x = а, то есть W(a) = 0.

Аналогичные рассуждения, проведенные для точки x = b, показывают, что W(b) = 0.

Свойство 1. Две собственные функции задачи Штурма-Лиувилля, соответствующие одному и тому же собственному значению λ, линейно зависимые.

Доказательство. Так как собственные функции являются решениями одного и того же однородного уравнения (17) (по условию число λ одно), то в случае их линейной независимости определитель Вронского не равен нулю ни в одной точке отрезка [а, b]. Это противоречит только что доказанной лемме. Следовательно, y₁(x) и у₂(x) — линейно зависимые функции.

Свойство 2. Две собственные функции у₁(x) и у₂(x), соответствующие различным собственным значениям λ₁ и λ₂ (λ₁ ≠ λ₂), на отрезке [а, b] ортогональны.

Доказательство этого свойства проведем для собственных функций такой задачи, в которой уравнение имеет вид (18). Составим определитель Вронского функций у₁ и у₂ и продифференцируем его:

Так как у₁ и у₂ — решения уравнения (18) при λ = λ₁ и λ = λ₂, соответственно, то получим

Проинтегрируем по отрезку [а, b] левую и правую части полученного равенства. С учетом леммы будем иметь

По условию λ₁ — λ₂ ≠0, следовательно
Функции y₁(x) 0 и у₂(х) 0, поэтому
Значит, y₁(x) и у₂(х) на отрезке [а, b] ортогональны.

Если уравнение, входящее в задачу Штурма-Лиувилля, имеет вид (17), где r(х) > 0 и r(x) 1, то под ортогональностью функций в этом случае подразумевают ортогональность с весом r(х): две функции y₁(x) и у₂(х) ортогональны на отрезке [а, b] с весом r(x), если

Под нормой функции ||у(x)|| в этом случае также подразумевают весовую норму:

Свойство 3. Собственные функции, соответствующие различным собственным значениям, образуют линейно независимую систему функций.

Это утверждение вытекает из попарной ортогональности собственных функций, соответствующих различным собственным значениям (см. свойство 2).

Свойство 4. Собственные значения задачи Штурма-Лиувилля действительные.

Доказательство. Предположим, что задача Штурма-Лиувилля <L_λy = 0, l₁y = 0, l₂y = 0> имеет комплексное собственное значение λ = α + βi,β ≠ 0. Пусть ему соответствует собственная функция у(х) (вообще говоря, тоже комплекснозначная). Так как все коэффициенты уравнения и краевых условий имеют действительные значения, то

Здесь черта означает переход к комплексно сопряженному выражению. В нашем случае

Значит число также является собственным значением той же задачи Штурма-Лиувилля и ему соответствует собственная функция . Так как в силу свойства 2 функции y(x) и ортогональны на [а, b], то

Отсюда следует, что у(x) ≡ 0 на [а, b]. Значит ни одно комплексное число λ не может быть собственным значением.

Свойство 5. Пусть коэффициенты уравнения (17) удовлетворяют условиям: р(х), q(x), r(x) — непрерывные функции и, кроме того, р(х) имеет непрерывную производную на [а, b], р(х) > 0, q(x) > 0, r(х) > 0. Тогда задача Штурма-Лиувилля <L_λ y = 0, l₁ y = 0, l₂ y = 0> имеет бесконечное число собственных значений λ ₁, λ₂, . λ_n, . Если краевые условия имеют вид (19) или (20), или (21), то собственные значения соответствующей задачи Штурма-Лиувилля удовлетворяют неравенствам

Теорема Стеклова.Всякая непрерывная функция f(x), удовлетворяющая однородным краевым условиям : l₁f = 0 и l₂f = 0 , и имеющая непрерывные производные до второго порядка на отрезке [а, b], разлагается на этом отрезке в сходящийся ряд Фурье по собственным функциям y_n(х) задачи Штурма-Лиувилля <L_λ y = 0, l₁ y = 0, l₂ y = 0> :

где коэффициенты Фурье С_n вычисляются по формулам:

Эта теорема применяется при решении уравнений математической физики методом Фурье.

Решение задач Штурма-Лиувилля

Вначале рассмотрим уравнение (18) y» + λy = 0. и краевые условия первого рода (19) y(a) = y(b) = 0. Для удобства будем считать, что a = 0 и b = l > 0. К такой задаче можно всегда свести данную задачу, если сделать замену переменной x’ = x — a, при этом вид уравнения не изменится.

Вид общего решения уравнения (18) зависит от значений параметра λ. Разберем три случая: 1) λ 0. В первом случае обозначим λ = — k 2 . Тогда характеристическое уравнение r 2 — k 2 = 0 будет иметь действительные различные корни r₁ = k, r₂ = — k: Поэтому, общее решение дифференциального уравнения запишется в виде y = C₁e kx + C₂e -kx . Подставим краевые условия в общее решение и получим

Определитель этой системы равен

Следовательно, система имеет только нулевое (тривиальное) решение C₁ = C₂ = 0. Значит, при λ 2 и получим характеристическое уравнение r 2 + k 2 = 0. Оно имеет комплексные корни r₁ = ki и r₂ = -ki и общее решение дифференциального уравнения в этом случае запишется в виде y = C₁cos kx + C₂sin kx. Подставим краевые условия в общее решение:

(22)

Для того, чтобы эта система имела нетривиальные решения, необходимо и достаточно, чтобы sin kl = 0. Следовательно kl = πn, то есть Так как то можно ограничиться только положительными значениями n = 1, 2, . . Таким образом, собственные значения данной задачи имеют вид При этих значениях алгебраическая система (22) имеет решения:C₁ = 0, C₂ — любое действительное число. Подставим эти значения в общее решение дифференциального уравнения и получим собственные функции задачи

Обычно постоянный множитель выбирают либо равным единице, либо из условия нормировки:

По тому же алгоритму решаются задачи Штурма-Лиувилля следующего вида:

(23)

и

(24)

Эти задачи так же, как и предыдущая, при λ 0 не имеют собственных значений. В случае λ > 0 общее решение уравнения записывается в виде y = C₁cos kx +C₂sin kx, где После подстановки у в краевые условия, получим:

а) для задачи (23)

Для того, чтобы эти системы уравнений имели нетривиальные решения, необходимо и достаточно, чтобы coskl = 0. Следовательно, то есть Отрицательные значения n можно не рассматривать, так как Таким образом, собственные значения у этих задач одинаковые

Собственные функции задачи (23) имеют вид А у задачи (24) они другие:

Некоторые отличия возникают при решении задачи Штурма-Лиувилля в случае краевых условий второго рода

Рассуждениями, аналогичными тем, которые проводились для краевых условий первого рода, можно показать, что задача (25) при λ 0. В этом случае, общее решение уравнения имеет вид y = C₁cos kx + C₂sin kx, Найдем производную этой функции и подставим в нее краевые условия (25):

Эта алгебраическая система имеет нетривиальные решения тогда и только тогда, когда, sinkl = 0 то есть kl = πn или Таким образом, числа также являются собственными значениями задачи. Собственные функции при этих значениях имеют вид . Окончательно, задача (25) имеет собственные значения и собственные функции

Для задачи Штурма-Лиувилля с краевыми условиями третьего рода (21) уже не удается получить собственные значения в явном виде. В качестве примера рассмотрим одну такую задачу, когда

При задача (26) не имеет собственных значений и собственных функций. Доказательство этого проводится так же, как и для краевых условий первого рода. При λ > 0 общее решение уравнения записывается в виде y = C₁coskx + C₂sinkx, где . После дифференцирования этой функции и подстановки её производной и самой функции в краевые условия (26) будем иметь:

или

(27)

Получившаяся алгебраическая система будет иметь нетривиальные решения только в том случае, когда

coskl — ksinkl = 0 или

Уравнение (28) является трансцендентным уравнением относительно k. Оно не решается в явном виде. Однако, построив графики левой и правой частей уравнения (28), видно, что оно имеет бесконечно много решений (см. рис.13). Обозначим корни уравнения (28) через r_n, n = 1,2, . . Тогда при

Рис.13

Численными методами можно найти приближенные значения r_n. Из системы (27) при k = r_n получим C_1n = r_nC_2n , где C_2n -произвольные постоянные. При этих значениях постоянных решения дифференциального уравнения будут иметь вид

Они являются собственными функциями краевой задачи (26) с собственными значениями

Видео:Частное решение дифференциального уравнения. 11 класс.Скачать

Понятие о краевых задачах для дифференциальных уравнений

Помимо задачи с начальными условиями или задачи Коши в приложениях встречается и другая постановка задачи — значение искомой функции задается не в одной, а в двух точках, ограничивающих отрезок, на котором требуется определить решение. Такая задача называется краевой или граничной.

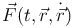
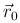
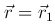
Например, в задаче о движении материальной точки массы m под действием заданной силы часто требуется найти закон движения, если в начальный момент t = t₀ точка находилась в положении, характеризуемом радиус-вектором , а в момент t = t₁ должна попасть в точку . Задача сводится к интегрированию дифференциального уравнения движения

с краевыми условиями .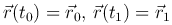

Заметим, что эта задача имеет, вообще говоря, не единственное решение. Если речь идет о баллистической задаче и о точках земной поверхности, то в одну и ту же точку тело может попасть по разным траекториям.

Рассмотрим краевые задачи для линейных уравнений второго порядка

краевые условия сводятся к нулевым условиям z(x₀)=z(x₁)=0, причем линейность дифференциального уравнения не нарушается. Умножим это уравнение на exp(∫p₁(x)dx), получим

где p(x)=exp(∫p₁(x)dx). Без ограничения общности изучение исходной краевой задачи можем заменить изучением следующей краевой задачи:

(1)

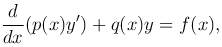
с граничными условиями

(2)

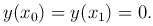
Пусть функция f(x) равна нулю на всем отрезке [x₀, x₁], за исключением ε-окрестности точки x=s, s — ε < x < s + ε, причем

Обозначим эту функцию f(x)=f_{ε(x, s)}.

Определение. Функцией Грина G(x, s) краевой задачи (1), (2) называется функция, удовлетворяющая следующим условиям:

• 1) G(x, s) непрерывна по x при фиксированном s при x₀ ≤ x ≤ x₁, x₀ ≤ s ≤ x₁;
• 2) G(x, s) является решением соответствующего однородного уравнения

на всем отрезке [x₀, x₁], за исключением точки x = s;
3) G(x, s) удовлетворяет граничным условиям:

является решением уравнения (1). Краевые условия (2) удовлетворяются по 2 свойству. Метод построения функции Грина. Рассмотрим решение y₁(x) уравнения

определяемое начальными условиями

Это решение, вообще говоря, не удовлетворяет второму граничному условию y(x₁)=0. Предполагаем, что не существует нетривиального решения y(x) этого однородного уравнения, удовлетворяющего нулевым граничным условиям y(x₀)=y(x₁)=0.

Очевидно, что решения C₁y₁(x), где C₁ — произвольная постоянная, также удовлетворяет граничному условию y(x₀)=0. Аналогично находим нетривиальное решение y₂(x) однородного уравнения, удовлетворяющее второму граничному условию y₂(x₁)=0. Этому же условию удовлетворяют все решения C₂y₂(x), где C₂ — произвольная постоянная.

Функцию Грина ищем в виде

причем постоянные C₁, C₂ выберем так, чтобы были выполнены свойства 1) и 4), то есть, чтобы функция G(x, s) была непрерывна по x при фиксированном s, и, в частности, непрерывна в точке x=s:

и чтобы G′_x(x, s) в точке x=s имела скачок l/p(s):

В силу предположения, что y₁(x₁) ≤ 0, решения y₁(x) и y₂(x) линейно независимы, так как все линейно зависимые от y₁(x) решения имеют вид C₁y₁(x) и, следовательно, при C₁ ≠ 0 не обращаются в нуль в точке x₁, в которой обращается в нуль решение y₂(x). Следовательно, определитель системы

являющийся определителем Вронского: W(y₁(x), y₂(x))=W(x) в точке x=s, отличен от нуля и постоянные C₁ и C₂, удовлетворяющие этой системе, легко определяются:

Видео:Дифференциальные уравнения | задача Штурма - Лиувилля | классические краевые задачи | 1Скачать

Начальные и граничные условия

Здравствуйте, продолжаем нашу рубрику по дифференциальным уравнениям, это уже 2 статья, если вы хотите начать сначала и ознакомиться с видами дифференциальных уравнений, то вам в первую статью.

Введение

Итак, для использования численных методов при решении дифференциального уравнения необходимо дополнительные условия. Если искомая функция(концентрация, температура и т.д) является функцией времени u=u(t), то требуются начальные условия, которые являются значением этой функции в момент времени, принятый за начальный:

Если начальная функция также зависит и от пространственных координат u=u(t,x), то начальное условие характеризуют ее распределение в пространстве в начальный момент времени:

В последнем случае помимо начальных условий требуются еще и граничные условия, которые имеют значения функции u(t,x) на границе изучаемой системы для любого момента времени. Причем, если искомая функция зависит от нескольких пространственных координат, то необходимо задавать граничные условия по каждой из них.

Небольшой пример

Например для следующего уравнения:

• начальное условие
• 2 граничных условия по координате
• 1 граничное условие по координате
• 2 граничных условия по координате

Сразу же возникает вопрос, почему именно так? Так вот, порядок производной определяет количество граничных условий для переменной. Как вы заметили, по y присутствует только первая производная, поэтому и одно граничное условие.

Классификация граничных условий

Для лучшего понимания рассмотрим классификацию на примере уравнения:

будет изменятся от до , соответственно при , будет левая граница, а при , будет правая.

Граничные условия 1-ого рода

Записываются следующим образом:

— функции, зависящие от , как пример:

Граничные условия 2-ого рода

Здесь вместо самих функций используются их первые производные.

Граничные условия 3-ого рода

Смешанные граничные условия

В этом случае левое и правое граничные условия могут быть разных родов:

Заключение

На этом мы подходим к концу нашей статьи. Сегодня мы с вами изучили начальные и граничные условия в дифференциальных уравнениях. Если вам что то осталось непонятным, то это нормально, не пугайтесь. В будущих статьях мы будем еще подробнее разбираться с этими и другими тонкостями, ну а на сегодня это все.

Спасибо, что прочитали статью, если у вас остались вопросы, то задавайте их в комментариях.
И, буду вам очень признателен, если вы вступите в нашу группу вконтакте, ссылка на которую размещена слева вверху под названием сайта.

📽️ Видео

Дифференциальные уравнения. 11 класс.Скачать

Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать

Общее и частное решение дифференциального уравненияСкачать

1. Что такое дифференциальное уравнение?Скачать

Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать

Краевая задача.Функция Грина.Дифференциальное ур.Скачать

Геометрический смысл дифференциального уравненияСкачать

Откуда появляются дифференциальные уравнения и как их решатьСкачать

18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать

Краевые Задачи для Обыкновенных Дифференциальных УравненийСкачать

Основные понятия дифференциальных уравнений от bezbotvyСкачать

Операционное исчисление. Решить неоднородное дифференциальное уравнение 2 порядкаСкачать

Задача Коши для дифференциальных уравненийСкачать

Решение физических задач с помощью дифференциальных уравненийСкачать

13. Как решить дифференциальное уравнение первого порядка?Скачать