МЕТОДЫ ПОЛУЧЕНИЯ ДИСКРЕТНЫХ АНАЛОГОВ
Дискретизацию дифференциального уравнения можно осуществить множеством способов.
Использование рядов Тейлора. Обычная процедура получения конечно-разностных уравнений заключается в аппроксимации производных в дифференциальном уравнении обрезанными рядами Тейлора.
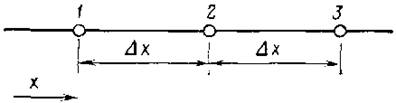
Рис. 2.1. Три последовательные узловые точки, используемые при разложении в ряд Тэйлора
Рассмотрим узловые точки, показанные на рис. 2.1. Разложение в ряд Тэйлора около узловой точки 2, расположенной посередине между точками 1 и 3 (так что 
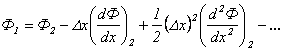 ; ; | (2.2) |
|---|
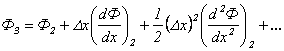 ; ; | (2.3) |
|---|
Отбрасывая члены обоих рядов, начиная с четвертого, вычитая и складывая уравнения, получаем
 | (2.4) |
|---|
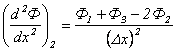 . . | (2.5) |
|---|
Подставляя эти выражения в дифференциальное уравнение, можно получить конечно-разностное уравнение.
В данном методе предполагается, что изменение 


Вариационный метод. Другой метод получения дискретных аналогов основывается на вариационном исчислении.
В вариационном исчислении показано, что решение данных дифференциальных уравнений эквивалентно минимизации соответствующей величины — функционала. Эта эквивалентность называется вариационным принципом. Искомый дискретный аналог получается из условий минимума функционала относительно значений зависимой переменной в узловых точках. Вариационный метод очень часто используется в конечно-элементных методах исследования напряжений, где его можно связать с принципом виртуальных перемещений. Кроме математической сложности и трудности понимания основным недостатком метода является его ограниченная применимость, связанная с тем, что вариационный принцип существует не для всех представляющих интерес дифференциальных уравнений.
Метод взвешенных невязок. Эффективным методом решения дифференциальных уравнений является метод взвешенных невязок. Основной подход прост и интересен. Представим дифференциальное уравнение в виде
 . . | (2.6) |
|---|
Предположим, что приближенное решение 
 ; ; | (2.7) |
|---|
где 


 . . | (2.8) |
|---|
Мы хотим сделать этот остаток в известном смысле малым. Предположим, что
 , , | (2.9) |
|---|
где 
Данный метод широко использовался для решения уравнений пограничного слоя, пока его почти не вытеснил метод конечных разностей. Однако можно установить его связь с конечно-разностным методом, или, точнее, с методом дискретизации, если рассматривать приближенное решение 

Простейшей весовой функцией является 
Метод контрольного объема. Часто в элементарных учебниках по теплообмену приводят вывод конечно-разностного уравнения с помощью метода рядов Тэйлора, а затем показывают, что результирующее уравнение соответствует условию теплового баланса в небольшой области, содержащей узловую точку. Мы также видели, что метод контрольного объема можно рассматривать как частный случай метода взвешенных невязок. Основная идея метода контрольного объема легко понятна и поддается прямой физической интерпретации. Расчетную область разбивают на некоторое число непересекающихся контрольных объемов таким образом, что каждая узловая точка содержится в одном контрольном объеме. Дифференциальное уравнение интегрируют по каждому контрольному объему. Для вычисления интегралов используют кусочные профили, которые описывают изменение 

Полученный подобным образом дискретный аналог выражает закон сохранения 
Результат решения дискретных уравнений относительно значений в узловых точках можно рассматривать двояко. В методе конечных элементов и большинстве методов взвешенных невязок в качестве приближенного решения берется предполагаемое изменение 


Для большей ясности применим метод контрольного объема к простой задаче.
Рассмотрим стационарную одномерную задачу теплопроводности, описываемую уравнением
 , , | (2.10) |
|---|
где 


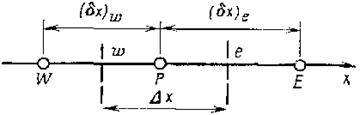
Подготовка. Для получения дискретного аналога будет использовано показанное па рис. 2.2 расположение узловых точек.
Рис 2.2. Шаблон узловых точек для одномерной задачи
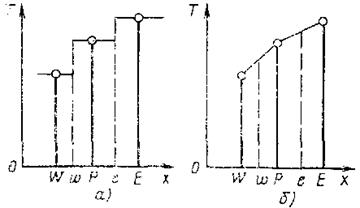
Рис. 2.3. Простые аппроксимации профилей:
а — ступенчатый профиль; б — кусочно-линейный профиль
В центре нашего внимания оказывается точка Р, окруженная точками Е и W (Е— восточная сторона, т. е. направление вдоль оси 




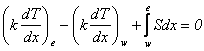 . . | (2.11) |
|---|
Предположение о виде профиля. Сделаем теперь предположение о виде профиля или интерполяционной формулы. На рис. 2.3 показаны два простых профиля. В простейшем случае предполагается, что значение 


Дискретный аналог. Использовав для определения 
 , , | (2.12) |
|---|
где 

 , , | (2.13) |
|---|
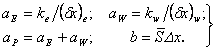 | (2.14) |
|---|
Необходимо сделать следующие примечания:
1. Уравнение (2.13) записано в стандартном виде. В левой части этого уравнения находится температура 

 , , | (2.15) |
|---|
где индекс 
2. При выводе уравнения (2.13) использовалось простейшее приближение для профиля, позволившее рассчитать 
3. Важно также понимать, что для различных величин можно использовать разные профили. Например, для вычисления 




4. Нет необходимости использовать одинаковые профили для всех членов одного уравнения. Например, если бы в уравнение (2.10) входил дополнительный член, включающий 

Основные принципы выбора интерполяционных функций и профилей. Указанная выше свобода выбора интерполяционных функций и профилей ведет к существованию множества способов получения дискретных аналогов уравнения. Предполагается, что при увеличении числа узловых точек решения всех дискретных аналогов исходного уравнения совпадают. Однако наложим дополнительное требование, которое приведет к сужению числа подходящих формул. Потребуем, чтобы решение, полученное даже на грубой сетке, во-первых, всегда имело физически правдоподобный характер и, во-вторых, сохраняло полный баланс.
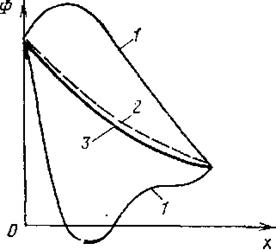
Рис. 2.4. Физически неправдоподобные (1), правдоподобное (2) и точное (3) решения
Понять, насколько физично полученное решение, легко, по крайней мере, в простых случаях (рис. 2.4). Правдоподобное решение должно иметь такой же качественный характер, что и точное решение. В задаче теплопроводности без источников никакой профиль температуры не может выходить за пределы температур границ тела. При охлаждении нагретого твердого тела окружающей его жидкостью температура тела не может стать ниже температуры жидкости.
Условие полного баланса предполагает интегральное сохранение рассматриваемой величины во всей расчетной области. Мы будет утверждать, что тепловые потоки, массовые расходы и потоки количества движения должны правильно отражать баланс с соответствующими источниками и стоками, причем для любого числа узловых точек, а не только в пределе при очень большом числе точек.
Такую возможность сохранения полного баланса дает метод контрольного объема, но при этом необходимо обеспечить, как вскоре увидим, правильный расчет потоков на границах контрольного объема.
Аппроксимация источникового члена. Прежде чем перейти к определению основных правил, рассмотрим источниковый член 


 , , | (2.16) |
|---|
где 




Наличие 




Дискретный аналог уравнения теплопроводности с линеаризованным источниковым членом будет иметь такой же вид, как и (2.13), но с другими выражениями для коэффициентов:
- Дискретизация дифференциальных уравнений
- О дискретизации линейных дифференциальных уравнений Текст научной статьи по специальности « Математика»
- Аннотация научной статьи по математике, автор научной работы — Егоршин Алексей Олегович
- Похожие темы научных работ по математике , автор научной работы — Егоршин Алексей Олегович
- ON LINEAR DIFFERENTIAL EQUATION DISCRETIZATION
- Текст научной работы на тему «О дискретизации линейных дифференциальных уравнений»
- 🎦 Видео
Видео:1. Что такое дифференциальное уравнение?Скачать

Дискретизация дифференциальных уравнений
В частных производных
Решением дифференциального уравнения называется функция непрерывного аргумента, обращающая это уравнение в тождество при заданных граничных и начальных условиях. При численном решении исходное дифференциальное уравнение (вместе с граничными и начальными условиями) заменяется эквивалентной системой алгебраических уравнений, а численным решением называется сеточная функция, обращающая указанную систему алгебраических уравнений в тождество.
Процесс замены дифференциального уравнения системой алгебраических уравнений называется дискретизацией, а сама алгебраическая система – дискретным аналогом дифференциального уравнения. Цель наших дальнейших действий заключается в изучении широко распространенных способов получения (построения) дискретных аналогов дифференциальных уравнений в частных производных.
4.1 Метод конечных разностей
Введенное в предыдущем параграфе определение сеточной функции естественным образом распространяется на случай двух и более аргументов. Простейшую двумерную сетку <xi,j, yi,j> можно построить как набор из J одномерных сеток, каждая из которых содержит I узлов, при этом должно выполняться условие:
xi-1, j
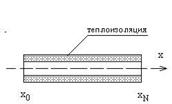
где Т – температура (подлежащая определению в результате решения), t – время, α – коэффициент теплопроводности, х – координата. С точки зрения физики, уравнение (21) описывает нестационарный процесс распространения тепла в стержне с теплоизолированной боковой поверхностью и возможностью подвода (отвода) теплоты на его торцах (рис. 6). С математической точки зрения, решением уравнения (21) является функция, зависящая от двух переменных (координата х и время t). Рис. 6. Стержень с теплоизолированной боковой поверхностью Для решения задачи должно быть заданы: § граничное условие на левом торце стержня – либо зависимость температуры от времени T0=T(x0,t) (условие Дирихле) либо пространственная производная § граничное условие на правом конце стержня – TN=T(xN,t) либо § начальное условие – закон распределения температуры по всей длине стержня в начальный момент времени Т(х, 0), где x0 Алгебраическое уравнение (21) позволяет методом «последовательного обхода» узлов расчетной сетки найти все неизвестные значения сеточной функции Ti, j:
Как следует из рассмотрения рис. 8а, в правой части уравнения (22a) упоминаются лишь те узлы расчетной сетки, значения температуры в которых уже известны. Расчетные схемы, обладающие указанным свойством, называются явными. Данное обстоятельство, с одной стороны, существенно упрощает решение задачи об отыскании значений сеточной функции Тi, j, с другой стороны, анализ формулы (22a), показывает, что температура в узле xi в момент времени tj+1, зависит только от температуры в узлах xi-1, xi, xi+1 в момент времени tj, и не зависит от распределения температур внутри стержня в момент времени tj+1, что не вполне соответствует физическому смыслу задачи. Для устранения этого противоречия, несколько видоизменим аппроксимацию производной
Правая часть уравнения (23a) содержит неизвестные величины Ti-1,j+1 и Ti+1,j+1, поэтому оно не может быть непосредственно (без увеличения объема вычислительной работы) использовано для нахождения температуры Ti,j+1. Расчетный шаблон для неявной расчетной схемы (23a) приведен на рис. 8б. Как показывают оценки [Флетчер], объем вычислений, при применении неявной схемы вместо явной схемы (22a), возрастает, ориентировочно, в два раза. Однако лучшая физическая обоснованность неявной схемы позволяет нам рассчитывать на более высокое качество результатов расчета. В качестве примера, обсудим решение неявного уравнения (23а) методом итераций(Гаусса-Зейделя). Первый этап метода заключается в выборе начального приближения для искомых значений функции. В данном случае, хорошей идеей представляется использование в качестве начального приближения значений температуры, взятых с предыдущего временного слоя, т.е.
где верхний индекс означает номер итерации. Тогда, с учетом (23а), в первом приближении температура в момент времени tj+1 может быть определена как
Скорее всего, значения температуры, определенные в первом приближении, не будут удовлетворять исходному уравнению (23). Поэтому процесс придется продолжать до тех пор, пока для каждого узла сетки различие между результатами, полученными на очередной и предыдущей итерациях, не станет меньше некоторой наперед заданной величины (точности решения) ε, т.е. пока не будет выполнено условие:
Следует также предусмотреть прекращение расчета в том случае, если решения не удастся достигнуть (решение не сойдется) после некоторого «разумного» числа итераций К. Причиной отсутствия сходимости, в частности, могут стать завышенные требования к точности решения ε, чрезмерно большие шаги расчетной сетки Δx и Δt, неудачный выбор начального приближения, а также некоторые физические эффекты[23]. В некоторых случаях, добиться сходимости решения удается за счет использования метода релаксации. Преобразуем последнюю из формул (25) к виду:
где r – коэффициент релаксации (r>0). Очевидно, что, при r=1, формула (25а) совпадает с последней из формул (25). При значениях 0 1 (верхняя релаксация), может привести к сокращению продолжительности расчета, а может вызвать полный «развал» численной схемы. Следует подчеркнуть, что выбор метода дискретизации дифференциальных уравнений и оптимальной величины коэффициента релаксации возлагается на исследователя[25]. Дополнительные сведения по этому вопросу содержатся в главе, посвященной свойствам разностных схем. 4.2 Метод конечных элементов В основе метода конечных элементов (МКЭ) лежит предположение о характере поведения функции Очевидно, что значение кусочно-линейной функции Ф*=Ф(х*) в некоторой точке х*, лежащей внутри отрезка [xi-1, xi] может быть найдено по формуле: Рис. 9. Кусочно-линейная интерполяция решения дифференциального уравнения
График функции формы (пробной функции) Рис. 10. Линейная функция формы Отметим также, что производная кусочно-линейной функции Ф(х) в пределах элемента [xi-1, xi] совпадает с конечно-разностным отношением назад (9а), а в пределах элемента [xi, xi+1] – с конечно-разностным отношением вперед (9b). Продемонстрируем применение метода конечных элементов на примере рассмотренного нами ранее обыкновенного дифференциального уравнения (13). Для сокращения записи будем использовать обозначение F(x)= Подстановка в уравнение (13) вместо точного решения
где R(х) – невязка решения, в общем случае являющаяся функцией независимой переменной х. Очевидно, что кусочно-линейная функция Ф(х) будет хорошим приближением к точному решению Второй принципиальный этап МКЭ заключается в выборе способа определения неизвестных узловых значений Фi. Для решения этой задачи потребуем, чтобы взвешенные интегралы невязки по всей области задания функции
Вследствие локальности функций формы
Все интегралы, входящие в (30а), могут быть сравнительно легко определены, а сами соотношения (30а), совместно с начальным условием Ф0=
Следует обратить внимание на то, что матрица системы линейных алгебраических уравнений (30b) имеет специфическую диагональную (ленточную) структуру. Для решения систем уравнений с ленточными матрицами, в вычислительной математике разработан ряд специальных методов, позволяющих существенно уменьшить объем вычислительной работы, самый распространенный из этих методов, называется методом прогонки. Результаты решения дифференциального уравнения (13) методом конечных элементов приведены на рис. 11. Как можно видеть из этого рисунка, уже при шаге сетки Δх=0,08 численное решение, полученное с помощью МКЭ, гораздо лучше соответствует точному решению, чем численное решение, полученное с помощью метода Эйлера при шаге сетки Δх=0,025 (см. рис. 4). Следует, однако, отметить, что объем вычислительной работы, связанный с определением интегралов, входящих в (30), и последующее решение полученной системы алгебраических уравнений, на порядок превосходит объем вычислительной работы, выполненной по методу Эйлера. Метод конечных элементов естественным образом распространяется на случай функций нескольких переменных. При этом, как правило, оказывается удобнее задавать каждую из функций формы в локальной системе координат, связанной с рассматриваемым узлом расчетной сетки. В качестве примера, на рис. 12 приведен график полилинейной функции формы Рис. 11. Решение дифференциального уравнения (13) методом конечных элементов Рис. 12. Полилинейная функция формы содержащей треугольные конечные элементы 4.3 Метод конечных объемов Использование метода конечных (контрольных) объемов продемонстрируем на примере двумерного стационарного уравнения теплопроводности:
где α – коэффициент теплопроводности, S – скорость выделения теплоты в единице объема. Решение задачи начнем с построения разностной сетки и разбиения расчетной области на непересекающиеся ячейки (объемы), каждая из которых содержит лишь один узел сетки (рис. 13). Проинтегрируем уравнение (31) по объему ячейки А:
Рис. 13. Расчетная сетка, используемая для решения уравнения (31) методом конечных объемов Используя теорему о среднем можно записать
где Δх, Δу – длины граней ячейки, xW – абсцисса левой («западной») границы ячейки А, xЕ – абсцисса правой («восточной») границы, уN – ордината верхней («северной») границы, уS – ордината нижней («южной») границы, S* – средняя по ячейке скорость тепловыделения. Индекс у производных (*), в левой части (32), указывает на то, что их следует рассматривать как средние значения, определенные таким образом, чтобы правильно представить тепловые потоки на каждой из границ. С учетом данного обстоятельства, дискретный аналог (32) может быть получен без затруднений [Патанкар]. Таким образом, уравнение (32) описывает баланс тепла (закон сохранения энергии) в пределах ячейки А. При условии правильного описания тепловых потоков между ячейками, система, составленная из уравнений вида (32), примененных к каждому контрольному объему, будет верно описывать баланс тепла во всей расчетной области. В завершение параграфа следует отметить, что в частных случаях расчетные формулы, полученные описанными выше способами, могут совпадать, а наиболее существенные отличия проявляются при использовании криволинейных неортогональных расчетных сеток. Видео:18+ Математика без Ху!ни. Дифференциальные уравнения.Скачать  О дискретизации линейных дифференциальных уравнений Текст научной статьи по специальности « Математика»Видео:Дифференциальные уравнения. 11 класс.Скачать  Аннотация научной статьи по математике, автор научной работы — Егоршин Алексей ОлеговичРассмотрены некоторые вопросы получения дискретного описания дифференциальной системы (ДС) на равномерной сетке. Рассматриваются ДС в виде системы n линейных обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами или одно уравнение n-го порядка для наблюдаемого функционала состояния ДС. Изучаемые вопросы дискретизации важны для задач вариационной идентификации и аппроксимации динамических процессов моделями этого типа в конечном интервале. Дано сравнение аналитического равномерного (на основе теоремы Гамильтона-Кэли ) и локальных методов дискретизации: на основе разделенных разностей и с помощью интерполяции выборок из n +1 отсчетов многочленами Тейлора степени n. Получена общая формула локальной дискретизации , прозволяющая сравнивать ее разностный и интерполяционные методы. Показано с использованием свойств обратных матриц Вандермонда , что в полученной общей формуле локальной дискретизации ее интерполяционному методу соответствуют (n + 1)-матрицы Тейлора (из коэффициентов многочленов Тейлора), а разностному — (n + 1)-матрицы Паскаля (из чисел треугольников Паскаля ). Показано, что невырожденность матрицы наблюдаемости ДС на сетке есть необходимое и достаточное условие как для аналитической дискретизируемости, так и для приведения дискретной системы (описания ДС сетке) к каноническому фробениусовскому виду. Он эквивалентен одному обыкновенному разностному уравнению для наблюдаемой переменной с постоянными коэффициентами. Это уравнение есть основа известного вариационного метода идентификации. Показано, что интерполяционный метод локальной дискретизации есть первое (линейное) приближение формулы равномерной аналитической дискретизации . Показано, что нулевое приближение ее не зависит от коэфффициентов ДС и есть вектор коэффициентов n-й разности. Показано также, что нулевое приближение матрицы наблюдаемости ДС н и матрицы наблюдамости полиномиальной системы y (n) =0 на сетке есть n-матрица Тейлора. Видео:Частное решение дифференциального уравнения. 11 класс.Скачать  Похожие темы научных работ по математике , автор научной работы — Егоршин Алексей ОлеговичВидео:Дифференциальные уравнения, 1 урок, Дифференциальные уравнения. Основные понятияСкачать  ON LINEAR DIFFERENTIAL EQUATION DISCRETIZATIONSome problems of obtaining the discrete description of the first order differential system (DS) on the uniform lattice have been considered. These DS are regarded in the form of system n of the first order ordinary linear differential equations with constant coefficients or as one n-order equation for the observed functional of the DS state. The problems under consideration are of some importance for the problems of the variational identification and approximation of the dynamic processes by means of that type models on the finite interval. There are compared the analytic uniform method of discretization (based on Cayley Hamilton theorem ) and that of the local one on the basis of the interpolation of the samples of n + 1 counting by Taylor polynomials to the power n. There have been obtained the general formula of the local discretization that makes it possible to compare its difference and interpolarization methods. It has been shown by using Vandermond inverse matrices that in the obtained general formula of the local discretization n +1 Taylor matrices (from Taylor polynomial coefficients) correspond to its interpolational method while n+1 Pascal matrices (from Pascal triangle numbers) correspond to the difference method. It has been shown that matrix nondegeneracy of the DS observability on the lattice is a necessary and sufficient condition both for analytic discretizability and for reducing the discete system (of the DS description of the lattice) to Frobenius canonical form. It is equivalent to one ordinary difference equation for the observed variable with constant coefficients. This equation is a basis of the well-known variational method of identification. It has been shown that interpolation method of the local discretization is the first order linear approximation of the uniform analytic discretization formula. It has been demonstrated that its zero order approximation does not depend on the DS coefficients and is a vector of the coefficients of the n-th difference. We conclude that zero order approximation of the observability matrix of DS and of the observability matrix of the polynomial system y( n) =0 on the lattice is Taylor n-matrix. Видео:Откуда появляются дифференциальные уравнения и как их решатьСкачать  Текст научной работы на тему «О дискретизации линейных дифференциальных уравнений»О ДИСКРЕТИЗАЦИИ ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Рассмотрены некоторые вопросы получения дискретного описания дифференциальной системы (ДС) на равномерной сетке. Рассматриваются ДС в виде системы п линейных обыкновенных дифференциальных уравнений первого порядка с постоянными коэффициентами или одно уравнение п-го порядка для наблюдаемого функционала состояния ДС. Изучаемые вопросы дискретизации важны для задач вариационной идентификации и аппроксимации динамических процессов моделями этого типа в конечном интервале. Дано сравнение аналитического равномерного (на основе теоремы Гамильтона-Кэли) и локальных методов дискретизации: на основе разделенных разностей и с помощью интерполяции выборок из п +1 отсчетов многочленами Тейлора степени п. Получена общая формула локальной дискретизации, прозволяющая сравнивать ее разностный и интерполяционные методы. Показано с использованием свойств обратных матриц Вандермонда, что в полученной общей формуле локальной дискретизации ее интерполяционному методу соответствуют (п + 1)-матрицы Тейлора (из коэффициентов многочленов Тейлора), а разностному — (п + 1)-матрицы Паскаля (из чисел треугольников Паскаля). Показано, что невырожденность матрицы наблюдаемости ДС на сетке есть необходимое и достаточное условие как для аналитической дискретизируемости, так и для приведения дискретной системы (описания ДС сетке) к каноническому фробениусов-скому виду. Он эквивалентен одному обыкновенному разностному уравнению для наблюдаемой переменной с постоянными коэффициентами. Это уравнение есть основа известного вариационного метода идентификации. Показано, что интерполяционный метод локальной дискретизации есть первое (линейное) приближение формулы равномерной аналитической дискретизации. Показано, что нулевое приближение ее не зависит от коэфффициентов ДС и есть вектор коэффициентов п-й разности. Показано также, что нулевое приближение матрицы наблюдаемости ДС н и матрицы наблюда-мости полиномиальной системы у(п) =0 на сетке есть п-матрица Тейлора. Ключевые слова: вариационная аппроксимация и идентификация, дискретизация дифферециальных уравнений, аналитическая дискретизация, линейное приближение, теорема Гамильтона-Кэли, локальная дискретизация, многочлены Тейлора, матрица Вандермонда, треугольник Паскаля. Дискретизацией дифференциального уравнения называем получение разностного уравнения, описывающее отсчеты решения дифференциального уравнения на заданной Л,-сетке. Мы говорим об однородных уравнениях. Вопрос о дискретизации становится актуальным при решении некоторых задач идентификации (оценки коэффициентов) дифференциальных уравнений, для которых удовлетворительные методы решений существуют лишь для их разностных аналогов. К таким задачам относятся, в частности, вариационные задачи идентификации [1]. Отметим два подхода к дискретизации дифференциальных уравнений: локальной — с помощью конечных разностей (он в некоторых случаях применим и для уравнений с переменными коэффициентами) и равномерной. Один из них — аналитический метод дискретизации на основе теоремы Гамильтона-Кэли [2]. Он дает разностное уравнение для отсчетов на Л,-сетке любого решения ДУ на любом интервале. И дифференциальные уравнения (ДУ), дискретизации которых посвящена статья (обыкновенные линейные уравнения с постоянными коэффициентами), и получаемые разностные уравнения (РУ) есть, с точки зрения идентификации и математического моделирования, некоторые (наиболее простые в нашем случае) модели реальных динамических процессов. Поэтому для обозначения исходных данных (идентифицируемых реальных процессов) используются обычные латинские буквы (например, y(t)), а их описания с помощью моделей отмечаем надсимвольным знаком, в данном случае, y(t). Условимся и о других обозначениях. Конструкции вида m будут обозначать вектор-столбец, | Xj |П или |xi, . xn| — вектор-строку, а m]n — матрицу (i — номера строк) множества элементов вида x. Они могут быть и скалярами, и строками, и столбцами, и матрицами. Если элементы xi в <x^^ — (n — l + 1)-векторы-строки, а xj в |xjЩ или в |xi. xn| — (m — k+1)-векторы-столбцы, то эти конструкции определяют матрицу m]n-Верхний индекс * у скаляров обозначает комплексное сопряжение. У векторов и матриц, в том числе и действительных — он обозначает еще и транспонирование. Нумерация L + 1 узлов ti, i = 0, L, h-сетки с L ячейками интервале наблюдения Ту, T = Lh ведется с нуля. Поэтому нумерация и отсчетов y*, i = 0, L решетчатой функции y* — строки y* = |y*|o, и компонент (L + 1)-вектора y = ° € E = E0+1 ведется также с нуля. Последовательность длины L + 1 из l2 [L] компонент вектора y называется далее реализацией (отсчетов yi, i = 0, L). С нуля ведется и нумерация других элементов в используемых евклидовых пространствах E = E0+1, En+1, En. Первая позиция этих и других векторов считается нулевой. Это согласуется с нумерацией компонент в векторах производных — векторах состояний дифференциальных уравнений. С нуля нумеруются и орты (столбцы) в евклидовых пространствах. Канонические орты обозначаются так: в E — это ej = e.j/L+1 = №,j>о, j = 0, L, в En+1 — это ej/n+1, j = 0,n ив En — это e j/n, j = 0,n — 1. В частности, eo/n = |1, 0^.-11* и en_1/n = |0^-1, 1|* — есть соответственно первый и последний n-й орты в En. Здесь и далее 0^ — нулевой к-вектор-столбец, а 0^ — нулевой k-вектор-строка. Аналогичные орты ej = (•, ej ), ej/n+1 = ( ‘, ej/n+) , ej/n = ( ■, ej/n) в сопряженных пространствах — E1 = E/0+1, E/n+1, E/n — будут обозначаться как e*, e* . ,, e* соответственно. 1. Аналитическая равномерная дискретизация 1.1. Модели вариационной идентификации Для получения аппроксимации функций y(t) € L2 минимизируется выпуклый функционал метода наименьших квадратов (МНК) — Jc = ||y(t) — y(t) ||0,2, где L2 = L2[It ], It = [0,T ]. (1) Здесь y(t) € C(n)[Iy] — переходные процессы линейных обыкновенных ДУ с постоянными коэффициентами — Задача аппроксимации (1), (2) при неизвестных коэффициентах a уравнения (2) является задачей их вариационного оценивания (идентификации) [1]. Такая постановка задачи аппроксимации (функционал (1) и ДУ (2) в качестве условий его минимизации) есть обобщение задачи МНК-аппроксимации функций полиномом степени n — 1 на конечном интервале. Это легко увидеть, если указанную известную задачу сформулировать аналогичным образом: минимизировать Jc из (1) при условии, что y(n) = 0. Для аппроксимации решетчатых функций у = о £ Е^1 = Е на Л,-сетке мы используем функционал МНК в Е (или, что то же, в 12[Ь]) а в качестве условий его минимизации — РУ вида, аналогичного (2) (линейное, однородное с постоянными коэффициентами) для реализации у £ Е. Пусть к = 0,Ж, N = Ь — п, у = у(^), ^ £ 4, г = 0,Ь, тогда ^=0 ук+г«* =0 = (у ,а)Еп+1 , где у = [у]; = о и а„ = 0. Векторы вида V подряд следующих отсчетов из их последовательности у £ Е = Ео+1 называются далее выборками. Векторы V;, к = 0, N из (4) являются (п + 1)-выборками — (п + 1)-векторами из Ео+1. Для вычисления и прогнозирования решения РУ (5) важна его рекуррентная форма: у;+п = — ^ у;+га* = —(у;, а>Еп, где ^ = [У]; = о—1 (6) — вектор состояния модели динамической системы, описываемой уравнением (5). Вектор а * назван прогнозирующим вектором коэффициентов РУ (5), (6). Уточним эти обозначения для коэффициентов РУ (5) и ДУ (2): а * = | а0. а**—1,а0|, если ао = 1, то >к >к >к >к 1 а = 1 а0. ап—1, ап|, если ао = 1, то Запишем ДУ (2) в эквивалентной канонической форме линейной системы п уравнений первого порядка с фробениусовской матрицей перехода — еп— 1/оа*. Здесь /^ = 0— 1 — матрица сдвига, частично изометрический оператор в Ео. Вектором состояния динамической системы с матрицей перехода является «укороченный> п-вектор го производных наблюдаемого функционала у = (го*, в0/га)еп: го* = о— 1 • Пусть в ДУ (2) ао = 1. Тогда, если а = | а0. ап _ 1,11 = | а , 11, a = I a0. an _ 1, 11 = I a , 11. AF (a) In era_1/raa , то на It : wt = Afwt, yt = e0/nwt = (гоt,eo/n)E„ Вследствие теоремы Гамильтона-Кэли, для переходной матрицы B = exp (Af h) дискретной системы го^+1 = Bw& имеем равенство ^П a*e0/nB = 0, из которого и вычисляется вектор а * = |а0. а**_1,1| = |а*, 1| коэффициентов РУ (5), (6), если положить an = 1. 1.2. Матрица наблюдаемости на равномерной сетке Пусть имеется система п дифференциальных уравнений с наблюдаемым значением у(£) линейного функционала в * = в! = (•,^)Ёп € Е/га на п-векторе состояния ж(£): ж(і) = Аж(і), у(£) = й*ж(£) = (ж(і), й)Еп , і Є /т = [0, ЬЛ,]. Дискретный аналог системы (9) на сетке /^ (3) для Ск = зс(кН), к = 0, Ь: Ок+1 — ФхСк, ук+п — й ОСк+п — (З’к+Ъ Ф Определим операторы наблюдаемости ^к = П—о1, к = 0, N. Эти операторы определяют связь между состояниями систем (10) и (6). Образуем линейную функцию , к = 0, N значений у(^), г = 0, £ наблюдаемого функционала (•, в) в (9) на сетке : — матрицы наблюдаемости дискретной системы (10) или, точнее, матрица наблюдаемости дифференциальной системы (9) на Л,-сетке интервала /у. Выборки Ук есть п-векторы состояния эквивалентной уравнению (6) следующей дискретной системы с канонической матрицей Фу фробениусовского типа (см. (8)). тогда ^к+1 = ФуСк, Ук+п = еП—1/п^к+1 = ^Ск+1, вп—1/п 1.3. Равномерная аналитическая дискретизация Рассмотрим две задачи анализа системы (9) на сетке /^ с помощью матрицы ^ наблюдаемости дифференциальной системы (9) на этой сетке. Обе эти задачи приводят к формуле равномерной аналитической равномерной дискретизации любого решения системы (9). Первая — на основе теоремы Гамильтона-Кэли, вторая — с помощью преобразования системы (10) к каноническому виду (13). Теорема 1. Обратимость матриц ^к, к = —п, N наблюдаемости системы (9) на сетке /^ есть необходимое и достаточное условие для решения следующих задач. я. Равномерная аналитическая дискретизация: получение коэффициентов РУ (6) для вычисления отсчетов любого решения ДУ (1) на сетке /^ интервала /у. Ь. Получение любого решения системы (9) на сетке /^ для наблюдаемой переменной с помощью РУ (6) или дискретной системы (13) с фробениусовской матрицей Фу. Доказательство. Во-первых, отметим, что невырожденности матриц наблюдаемости ^к, к = —п, N необходима невырожденность матрицы Ф дискретной системы (10). а. Пусть а * — характеристические числа матрицы Ф системы (10). Тогда, по теореме Гамильтона-Кэли, Фг+ка* = 0 для всех к = 0, N. Это тождество, во-первых, дает из (11) разностное уравнение (5). Во-вторых, поскольку вектор ж° произволен, то, положив а« = 1, из тождества Гамильтона-Кэли получаем, для прогнозирующего вектора а* алгебраические уравнения при любом конечном к. Для их решения необходима и достаточна невырожденность матрицы V: Ь. От системы (10) с переходной матрицей Ф общего вида не трудно заменой переменных V = ^°ж перейти к каноническому описанию (13) системы (10). Эти описания неразличимы с точки зрения наблюдаемой переменной — значений функционала у = ^*Ж. Определим: В * = кфч«-1, ь* = ^*ф° = ¿*, ь« = ^*Фга. Делая теперь в (10) указанную замену переменных ж = V, получим систему с вектором состояния 5к = [V] к = (Уг+к>о-1, к = 0, Ж, с матрицей перехода ФЕ и с наблюдателем ^: Ф^ = V Ф^-1, Ук+п = 41 ук+1 = ¿*^Г-1гаг;к+1 = ¿*^Т«г;к = -а*^- (16) Последнее равенство показывает, что рекуррентное уравнение (6) может рассматриваться и как наблюдатель, и как предсказатель. Покажем, что Ф^ в (16) есть матрица Фробениуса, а наблюдатель = е«_1/га из (13). С учетом определений (15) можем записать: Из последнего равенства в (17) очевидны тождества: В*В( 1) = /«_1 — единичная п — 1-матрица, а В*Ь° 1) = 0. Отсюда видим, что матрица Ф^ в (17) — матрица Фробениуса из (13), если обозначить Ь«^0-1 = —а*. Учет (15) приводит к формуле —а* = ^*^_« из (14). О каноническом наблюдателе. Пусть В* = (^*Фг_п+1>П_2. Тогда из (16) имеем: что и требовалось. Необходимость и достаточность обратимости матрицы V очевидна. □ 2. Локальная дискретизация и конечные разности 2.1. Дискретизация уравнения для полиномов Широко используемая альтернатива равномерной аналитической (точной) дискретизации — локальная приближенная дискретизация. Она осуществляется при помощи операторов = Дг/Лг, г = 0,п, конечных разделенных разностей ук, к = 0, N в пределах г + 1 ближайших к текущей точке к отсчетов ук реализации у. Такая локальная дискретизация основана на приближении решения полиномами порядка г = 1,п (п — порядок уравнения) на интервалах длины гЛ. В п. 1.1 было отмечено, что модель (2) для аппроксимации функций (сигналов) есть обобщение модели полиномиальной аппроксимации у](”) = 0, где £ € /у. Модель (5) есть аналогичное обобщение модели: ДгаУк = 0 = [ДТ?к, где [Д«]* = |(—1)»_’ С«|«, С« = п/ !(п — ;)! (19) для полиномиальной аппроксимации отсчетов на сетке /^ для к = 0, N. Здесь через Д« обозначен оператор разности порядка п, а через [Д«]* — (п + 1)-вектор-строка его коэффициентов С«. Это вектор-строка коэффициентов РУ (19). Прогнозирующую часть вектора коэффициентов рекуррентной формы РУ (19) отмечаем, как и ранее (см. (3),(5)) надсимвольной чертой: [Дга] = |(—1)”_гС«|« . Это значит, что отсчеты ук, к = 0, N полинома порядка п определяются рекуррентной формулой, аналогичной формуле (6): ук+1 = —[Дга] ««к = —(^к, [Дга])еп . (20) Далее мы опишем способ локальной дискретизации на основе интерполяции выборок отсчетов заданной функции на интервалах длины пЛ полиномами порядка п. Этот метод локальной дискретизации основан на интерполяции многочленами Тейлора и поэтому назван тейлоровским. В п. 2.4 мы покажем его связь с упомянутым выше методом и операторами разделеных разностей. Будет также показано, что локальная тейлоровская дискретизация есть линейное приближение к равномерной аналитической на основе теоремы Гамильтона-Кэли. 2.2. Матрицы Тейлора и Вандермонда Обозначим через /т(^) минимальный интервал (длины Лт), содержащий выборку -и(т) из т + 1 подряд следующих отсчетов реализации у. Если индекс и аргумент т опущены, то т = п, то есть длина выборки есть п + 1 или п как определено ранее для стандартных выборок V и V в уравнениях (5) и (6). Запишем для отсчетов выборки Vk(т) = ™, где к = 0, Ь — т представление с помощью их интерполяции многочленами Тейлора порядка т. Пусть ¿к+т = кЛ+г°Л — некоторая точка в окрестности точки ¿к выборки 5к В этой точке значение т производных полинома, интерполирующего отсчеты выборки, и аппроксимируемой по этим отсчетам функции совпадают. Представление для отсчетов ук+г, г = 0, т с помощью такого интерполирующего полинома может быть записано так: Vk(т) = Т« (г°) ■ ад(т) (¿к + т), где Т™ (г°) = (Т*«>т = < (к (г — г°))/^. (21) В формуле (21) через -ш(т)(£к + т) = (у(«) (¿к + т)>т° обозначен (т + 1)-вектор производных функции у(£) € С(га) в точке ¿к + т, а Тт(г°) — квадратная (т + 1)-матрица коэффициентов т-степенной интерполяции т + 1 отсчетов выборки Vk(т). Матрицы Т вида (21) мы называем матрицами Тейлора или тейлоровскими матрицами. Если индекс т = п, то он опускается. Если т = п — 1, то используется надсимвольная черта: Тга_1 = Т. Опускается и аргумент г°, если его значение не существенно. Основные его значения будут 0, п и матрицы Т(0), Т(п) для граничных точек интервала /«(V). Пусть для простоты т = п и пусть д = «. Матрица Тейлора Т из (21) может быть представлена в виде: Так определенную матрицу Ж = Ж(д) назовем матрицей Вандермонда. Ее компоненты: п + 1 степеней ; (строки) п + 1 чисел д = « (столбцы). Лемма 1. Последняя строка т” 1)+ обратной матрицы Тейлора T 1 есть [Д”]*/h” — коэффициенты оператора D” = Дга/Л° разделенной разности порядка n, где [Д”]* = |(—1)0-jCj|”_0 (19), а Cj = n!/(n — j)!j! — коэффициенты бинома (s — 1)” = 5^0 Cj( —1)”-j sJ в порядке степеней s — оператора сдвига: syi = Уг+1- Доказательство. Этот факт следует из свойств матрицы Вандермонда и ее обращения, поскольку TT-1 = WDD-1W-1 = WW-1 = I. Из последнего следует, что столбец W-обратной матрицы W-1 Вандермонда W есть коэффициенты полинома n / n / n p(j)(A) = Y1 p(j)rAV= П(A — q^/^ , где ^ = П (qj— q^ j = 0>™ в порядке степеней Л. Поскольку коэффициент P(j)” = 1, то нормирующие множители 1/^j есть компоненты последней строки г,! 1)+ обратной матрицы Тейлора T-1, так как в соответствии с равенством WW-1 = I должно выполняться для всех i,j равенство ki |0_0 • ”_0 • Я-1 = Æij, где Æÿ — символ Кронекера. Далее. Из определений (21), (22) и выборок Vk, k = О, N следует, что числа qi + ¿0 = 0, n, то есть они есть отрезок натурального ряда. Следовательно, сомножители qj — qi в формуле для множителя ^j — две части указанного отрезка, разделенные числом j = 0, n. Поэтому Учтем снова представление (22), а именно, что T-1 = diag ” • W-1(q) (22). Последнее дает в последнню строку числа n!/(^jh”). Это и требовалось доказать. □ Следствие 1. Последняя (n + 1)-строка т(-1)* матрицы Тейлора T-1(i0) не зависит от точки ¿0. Число т(-1)*v есть оценка n-й производной в разложении Тейлора функции y(t) относительно средней точки интервала In. Тогда в (21): т = т0 = hî0n = hn/2 ^ ¿0 = n/2. Доказательство. Первое утверждение вытекает из леммы 1. Второе следует из того, что у n-полинома n-я производная — число т(-1)*v — постоянна. Это число — в силу симметричности коэффициентов вектора |( —1)”-jC”|” естественно считать оценкой производной y(n) (tk + т0) функции y(t) в средней точке т0 = hn/2 интервала In(vk) по ее разложению Тейлора на этом интервале относительно средней его точки т0. □ 2.3. Локальная тейлоровская дискретизация Лемма 2. Общая формула локальной дискретизации имеет вид где с — множитель, зависящий от вида матрицы T-1 (матрицы разностей) и нормировки вектора коэффициентов РУ (например, к единичной длине [3, 4] или к значению а0 = 1). Доказательство. Из (23) следует, что матрица Тейлора невырождена, если не вырождена соответствующая матрица Вандермонда. Как известно, определитель последней отличен от нуля, если все числа q различны. Пусть в (21) т = п. Тогда из полученной в (21) невырожденной системы алгебраических уравнений, получим выражения вида ад = Т-1^ для (п + 1)-векторов производных ад, определяющих ДУ (2). Подставляя эти выражения в уравнение(2) для значений £ на сетке , получим формулу локальной тейлоровской дискретизации: (ад^, а)£п + 1 = (Т % , а^> Еп+1 = ,Т а) Еп + ! = (Ук, а)йп + 1 что и требовалось. □ Представим матрицу Т в окаймленном виде с учетом ее общего представления (21): т* = |т*, $| , где $ = (Л(п — ¿0))7п! ^ $(п) = 0, Следствие 2. Если в лемме 2 матрица Т есть матрица Тейлора из (21), а нормировка вектора коэфффициентов а РУ (5) осуществляется к значению ап = 1 (как в уравнении (6)), то нормирующий множитель в формуле (23) леммы 2 равен: с = є ■ є 1, где є = $ — т*Т % є = 1 — а*Т «*• Доказательство. Используем формулу Фробениуса [2, 5] г = — _ 1—Т 1* , )* = — _1 —т*Т 1,1 и є = (т *) = ()* *) = $ — т *Т 1*. Умножая это слева на а*, получим требуемый результат. є = $ — т *Т 1* = $ + [Д”] Доказательство. Эти равенства следуют из представления последней строки матрицы Т 1 в формулах (26), (27) и из леммы 1. В соответствии с этими результатами є-1)* = є-11 — т*Т 11 = [Д”]*/Лга = |[Д™] , • Следствие 3. В формуле (23) тейлоровской дискретизации множитель с = Л”/є. Теорема 2. При тейлоровской локальной дискретизации формула для прогнозирующих коэффициентов имеет вид: = а * (єТ) 1 Л” + [Д”] *, где є = 1 — а*Т 1*, а * = Доказательство. Этот факт следует из леммы 2, из ее следствия, а также из равенств, установленных в лемме 3. □ 2.4. Конечные разделенные разности Наиболее известен метод дискретизации с помощью замены производных конечными разделенными разностями порядка от 0 до п. Лемма 4. Разностная дискретизация эквивалентна использованию в общей формуле локальной дискретизации (23) нижнетреугольной матрицы разностей Т-1. Строка г, г = 0, п ее треугольника с точностью до множителя К есть строка г знакопеременного треугольника Паскаля. В этом случае ап = 1, если в (23) множитель с = с д = Л”. Доказательство. По лемме 1 последние строки обратных матриц Тейлора Т* (21) размерности г + 1 есть (г + 1)-векторы коэффициентов разделенных разностей порядка г и эти векторы не зависят от точки т = Ыо разложения (21) выборок отсчетов V. Отсюда следует, во-первых, что метод конечных разностей означает использование в лемме 2 вместо матрицы Т-1 — обратной матрицы Тейлора вида (21) — нижнетреугольной матрицы Т- . Во-вторых, г-я строка ее треугольника есть вектор [Дг]*/К г-й разделенной разности. Матрица конечных разностей Т-1, следовательно, имеет вид: P_ij = 0 при j > i и P_ij = (—1)i-j при i ^ j. Если an = 1, то формула (23) примет вид а* = а* ■ T—1 ■ с д, где с д = hn. □ Нижнетреугольные матрицы вида P можно назвать матрицами Паскаля. Они имеют интересную особенность, используемую в доказательстве теоремы 3. Эта теорема отвечает на вопрос: какому представлению (виду интерполяции) отсчетов выборок v через производные (вместо тейлоровского v = Tw из (21)) соответствует их выражение v = Тд-w, вытекающее из способа дискретизации в лемме 4? Каков вид нижнетреугольной матрицы Тд? Теорема 3. Дискретизация ДУ разделенными разностями по формуле а* = а*Т_1hn эквивалентна, вместо их тейлоровского разложения (21), следующему представлению отсчетов выборок % с помощью нижнетреугольной матрицы Тд и чисел треугольника Паскаля: ¿0+ hj/2)j , = (i -ij.),j,. (29) Доказательство. При тейлоровском приближении Wk = Т-1ik производных на основе разложения (21), все n + 1 отсчетов выборки % интерполируются одним полиномом порядка n, и именно его производные в заданной точке т = hio принимаются в качестве оценок производных аппроксимируемой им функции. Ими заменяются производные в ДУ (лемма 4). Разностное приближение производных Wk = Т_1 % означает, что для оценки j-й производной используется «свой> полином j-го порядка. Как было показано в следствии леммы 1 (на примере полинома порядка n — n-полинома), j-я производная j-полинома, постоянная на минимальном интервале Р/(vk), содержащего эту (j + 1)-выборку, есть оценка j-й производной аппроксимируемой им функции y(t) в центре этого интервала, то есть в точке hj/2. Это и указано в формуле (29) теоремы 3. Определим оператор dT = sTd = (s — 1)/h, 0 ^ т ^ h разностного дифференцирования функции y(t) в точке tk + т: dTyk = sTd ■ yk = y;(tk + т). Здесь d = d/dt —оператор дифференцирования, а sT — символ сдвига sTy(tk) = y(tk + т) на величину т ^ h. Он указывает какой точке tk + т на интервале длины h значению производной y;(tk + т) приписывается значение разделенной разности ((в — 1)/Н)у^ . Наконец, в в операторе разности (в — 1) — «:обычный> оператор сдвига из леммы 3: ву^ = у^+ь Обратим оператор разностного дифференцирования йт = (в — 1)/Н, то есть выразим оператор сдвига в через оператор йт. Получим: в = йтН +1 и вУк = Ук+1 = (1 + Н^т )ук = (1 + Нвт ^)уй = ук + Ну'(¿й + т). Степени (йт)г = ((в — 1)/Н)г оператора йт (их коэффициенты) определяют строки матрицы Т-1 (28) и преобразование w = Тд1^, используемое для разностной дискретизации в лемме 4. Обратное нижнетреугольное преобразование (29) V = Т^, представлено в теореме 3. Его строки есть коэффициенты степеней вг = (йтН + 1)г оператора в. Представление (29) есть альтернатива тейлоровскому представлению (21). Докажем теперь формулу (29). Можно показать, что Р+Р_ = I, то есть Р—1 = Р+. Здесь Р+ — это матрица, аналогичная матрице Р_ из (28), но со знакопостоянными (положительными) числами треугольника Паскаля (без множителя ( — 1)г_ в компонентах Р^). В соответствии с леммой 4 матрица Тд = Р_1^_1 заменяет тейлоровскую матрицу Т в системе уравнений (21) для отсчетов: V = Tдw. Это означает использование для интерполяции отсчетов выборки % из РУ (5) вместо интерполяционного полинома (21) следующего формального разложения Отсюда получаем результат (29) — альтернативу разложения Тейлора (21): і-й отсчет выборки V есть сумма производных у(^(’’Н/2), j = 0, і с весами бинома і-й степени. □ 3. Линейное приближение равномерной дискретизации 3.1. Основной результат В этом разделе будет доказан следующий результат. Теорема 4. Линейным по а приближением к формуле (14) аналитической дискретизации а* = -^Р-Щ = -^*ФгаР-1, где Р = Р(А) = ^»1 = п_1, (30) является формула локальной тейлоровской дискретизации (23) леммы 2. Докажем вспомогательные и представляющие самостоятельный интерес утверждения. Лемма 5. Результат аналитической дискретизации по формулам (30) инвариантен к преобразованию фазовых координат в исходной системе (9). Доказательство. Пусть Ф = ехр(АуЛ) и Ф = ехр(АЛ) есть матрицы перехода дискретной системы (10) в случаях, когда исходная континуальная система (9) представлена в каноническом (8) и общем виде (9) соответственно. Матрицы наблюдаемости этих систем на сетке есть соответственно Р = Р(а) = Р(Ау) = Р(Ау(а)) = П и Р из (30). Заменой переменных ад = Рдх, где Рд = Щ 1 в (9) придем к равенству Ау = РдАРД-1. Отсюда выводим: Ф = РД 1фРд ^ Ф* = Рд1фгРд. Из замены переменных в (9) следует также, что е0/п = ¿*Рд1 = й*|й, В| 1*, где В* = Щ 1 и, кроме того, F = Ігі*Р-1Ф^ Рд ^ F-1 = Р-1і?_1. Используем эти результаты в (30): Получили требуемое: результат дискретизации динамических систем, связанных преобразованием фазовых координат, одинаков. В частности, он одинаков для общего (9) и канонического (8) описаний. Этот результат (31) и необходим для доказательства теоремы 4. □ 3.2. Полиномиальная система и нулевое приближение Лемма 6. Первая строка т0 1) + (п) обратной матрицы Тейлора Т 1(п) на (п — 1)-выборке с точкой разложения п, следующей за правой граничной точкой /га_1^) интервала интерполяции выборки V (п — 1)-полиномом, есть — [Дп] — прогнозирующий вектор п-й конечной разности с обратным знаком. Доказательство. Формула ад = Т 1(п) ■ V выражает п-вектор ад оценок производных (от 0-й до (п — 1)-й) через п-вектор отсчетов — п-выборку V. Поэтому, первая строка т0 ^*(п) матрицы Т (п) должна быть — со знаком «минуо — прогнозирущим вектором [Дп] коэффициентов разности Дп для прогноза значения нулевой производной (то есть отсчета самой функции) на точку п. Эта точка находится вне интервала /га_1(^), но в интервале РУ вида (5) для (п — 1)-полинома есть [Дга]* ■ V = 0. Прогнозирующий вектор его коэффициентов есть [Дп] , а рекуррентная формула прогноза (п — 1)-полинома, подобная уравнению (6) для РУ общего вида, есть у^+1 = — [Дп] ^. Коэффициенты правой части этого уравнения и есть компоненты первой строки матрицы Т (п). □ ___і __________^ _______і Следствие 4. е0/пТ (п) = — [Дп] = —т*Т . Доказательство. В результате леммы 6 нужно учесть первое равенство леммы 3. □ Полиномиальной системой мы называем систему п уравнений (8), если а = 0. Тогда в (8): Ау(а) = Ау(0) = /П — матрица сдвига. Эта система эквивалентна уравнению у(п) (¿) = 0, степенного полинома порядка п — 1 в заданном интервале /у. Лемма 7. Пусть дискретная система (10) описывает отсчеты полинома (п — 1)-й степени, то есть является реализацией полиномиальной (при а = 0, то есть Ау = Ау(0)) системы (8) на сетке /^. Матрица наблюдаемости (12) такой системы (8) на Н-сетке — ф = |e*/nфг j фk, где фг = фг(0) = exp (Ay(0)hi) — есть матрица Тейлора T(—k). Доказательство. Вычислим матрицу наблюдаемости F = F(0) = Fo (12) для этого случая: F = ie0/n Ф lo-1 = ie0/n eXP (JКак известно [2L exp (/lh) = En-1(h)j(11)У.Л- Следовательно, ф(i+k)(0) — верхнетреугольная теплицева матрица с числами (h(i + k))j/j! на j-й наддиагонали (на главной — j = 0). Ее первая строка e0/o Фг(0) = e0/o exp (/ 1h^ — есть |(hi)YjllO^o1- Это не что иное как i-я строка матрицы Тейлора T(—k) (21). Из выписанной выше формулы для матрицы наблюдаемости F следует, что ее i-я строка и есть i-я строка этой матрицы Тейлора. Лемма доказана. □ Доказательство. Для получения нулевого приближения надо положить а = 0 в формуле (31) для матрицы наблюдаемости F системы (8) на сетке □ Теорема 5. Нулевое по a приближение к аналитической дискретизации (30) есть оэффи-циенты уравнения для полинома (n — 1)-го порядка: а* = — [Дп] . Доказательство. Учтем, во-первых, лемму 5. Во-вторых, учтем в формуле (31) следствие 5, а именно, что F—n(0) = T (n). Результат леммы 6 и формула (31) для а* приводят к доказываемому утверждению. □ 3.3. Линейное приближение Доказательство теоремы 4. Для доказательства необходимо убедиться, что линейные приближения по a компонент формулы дискретизации (30) дают результат леммы 2 и теоремы 2. С учетом результата леммы 5 достаточно провести доказательство для дискретизации канонического описания (8). Будем исходить из первой формулы в (31): а* = —ео/п 1П ‘ F1-1 (Af(a)). Она доказывается несколько сложнее, но соответствует более общему случаю, когда угловая компонента $ = 0 в представлении (25) матрицы T. Получим сначала разложение Тейлора по степеням h до степени n включительно векторной функции — строки /* = /n(â) = e0/n Фп = e*/n exp (Af(â)hn), где Af(a) — матрица фробениуса из (8). Воспользуемся результатом леммы 7, где это разложение было получено до степени n — 1. Эти n членов ряда Тейлора функции e*/n Фn от вектора a не зависят, поскольку, как можно увидеть из формулы для матрицы Af в (8), e0/nAF р-1 = т » + т ^ 1 -ат ^ 1 ат «= т «+ т ч■ е_1■ ат Подставляем результат (32) и последнее выражение для Р-1 в первую формулу в (31): а* = — (т* — $а*) (т-1 + Т-1£ ■ е-1 ■ а*Т-1) = а*Т “V + а*Т-1£ ■ е-1 ■ а*Т-1$ — т*Т-1 — т*Т-1£ ■ е-1 ■ а*Т-1 = —*т^—1^ ,-1—*т^-Ча I гдп* ^*гг-^ ,-1 а*Т-1 = (е + â*T 1^Є—1â*T V + [Дга]* — т*T 1t ■ є — т*Т — 1^ е—1â*T—1 + [ДП]*. Это совпадает с результатом лемм 2, 3 и теоремы 2, с учетом формул (23) и (26). Теорема 4 доказана. □ Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 10-01-00035) и Сибирского отделения Российской академии наук (междисциплинарный проект № 80). 1. Егоршин, А.О. Идентификация стационарных моделей в унитарном пространстве / А.О. Егоршин // Автоматика и телемеханика. — 2004. — Т. 65(12). — С. 29-48. 2. Гантмахер, Ф.Р. Теория матриц / Ф.Р. Гантмахер. — М.: Наука, 1966. 3. Егоршин, А.О. Об отслеживании параметров экстремума в вариационной задаче идентификации / А.О. Егоршин // Вестник НГУ. Серия: Математика, механика, информатика. — 2011. — Т. 11, вып. 3. — С. 95-114. 4. Егоршин, А.О. Об одном способе оценки коэффициентов моделирующих уравнений для последовательностей / А.О. Егоршин // Сиб. журн. индустр. матем. — 2000. — Т. 3, № 2. 5. Эльясберг, П.Е. Определение движения по результатам измерений / П.Е. Эльясберг. -М.: Либроком, 2011. Алексей Олегович Егоршин, кандидат физико-математических наук, старший научный сотрудник, Институт математики им. С.Л. Соболева СО РАН, egorshin@math.nsc.ru. MSC 65F25; 15A03 On Linear Differential Equation Discretization A.O. Egorshin, Sobolev Institute of Mathematics, Siberian Branch of the Russian Academy of Sciences (Novosibirsk, Russian Federation) Some problems of obtaining the discrete description of the first order differential system (DS) on the uniform lattice have been considered. These DS are regarded in the form of system n of the first order ordinary linear differential equations with constant coefficients or as one n-order equation for the observed functional of the DS state. The problems under consideration are of some importance for the problems of the variational identification and approximation of the dynamic processes by means of that type models on the finite interval. There are compared the analytic uniform method of discretization (based on Cayley — Hamilton theorem) and that of the local one on the basis of the interpolation of the samples of n +1 counting by Taylor polynomials to the power n. There have been obtained the general formula of the local discretization that makes it possible to compare its difference and interpolarization methods. It has been shown by using Vandermond inverse matrices that in the obtained general formula of the local discretization n +1 Taylor matrices (from Taylor polynomial coefficients) correspond to its interpolational method while n+1 Pascal matrices (from Pascal triangle numbers) correspond to the difference method. It has been shown that matrix nondegeneracy of the DS observability on the lattice is a necessary and sufficient condition both for analytic discretizability and for reducing the discete system (of the DS description of the lattice) to Frobenius canonical form. It is equivalent to one ordinary difference equation for the observed variable with constant coefficients. This equation is a basis of the well-known variational method of identification. It has been shown that interpolation method of the local discretization is the first order linear approximation of the uniform analytic discretization formula. It has been demonstrated that its zero order approximation does not depend on the DS coefficients and is a vector of the coefficients of the n-th difference. We conclude that zero order approximation of the observability matrix of DS and of the observability matrix of the polynomial system y(n) =0 on the lattice is Taylor n-matrix. Keywords: variational approximation and identification, discretization of differential equation, analytical discretization, linear approximation, Cayley — Hamilton theorem, local discretization, Teylor polynomial, Vandermond matrices, Pascal triangle. 🎦 ВидеоЗадача Коши ➜ Частное решение линейного однородного дифференциального уравненияСкачать  13. Как решить дифференциальное уравнение первого порядка?Скачать  Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентамиСкачать  Лукьяненко Д. В. - Дифференциальные уравнения - Лекция 1Скачать  Основные понятия дифференциальных уравнений от bezbotvyСкачать  Проверить, является ли функция решением дифференциального уравнения #calculus #differentialequationСкачать  Однородные дифференциальные уравнения первого порядка #calculus #differentialequation #maths #Скачать  7. Линейные дифференциальные уравнения первого порядка. Метод Бернулли.Скачать  2. Дифференциальные уравнения с разделяющимися переменными. Часть 1.Скачать  Решение дифференциальных уравнений. Практическая часть. 11 класс.Скачать  Простейшие дифференциальные уравненияСкачать  |
 ,
,
 (условие Неймана);
(условие Неймана); ;
; ,
, в уравнении (21):
в уравнении (21): ,
, .
. , для всех[22] i=1 … N-1
, для всех[22] i=1 … N-1 ,
,  , …,
, …, 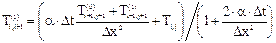 .
. , для всех i=1 … N-1.
, для всех i=1 … N-1. ,
, , являющейся точным решением дифференциального уравнения. Для демонстрации основных идей МКЭ, предположим, что с достаточной точностью искомое решение
, являющейся точным решением дифференциального уравнения. Для демонстрации основных идей МКЭ, предположим, что с достаточной точностью искомое решение 
 ,
,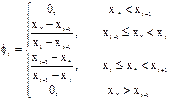 .
. , приведен на рис. 10. Необходимо отметить, что функция формы, является локальной, т.е. она отлична от нуля лишь в некоторой области, непосредственно прилегающей к рассматриваемому узлу xi. В частности, в случае кусочно-линейной интерполяции функции одной переменной
, приведен на рис. 10. Необходимо отметить, что функция формы, является локальной, т.е. она отлична от нуля лишь в некоторой области, непосредственно прилегающей к рассматриваемому узлу xi. В частности, в случае кусочно-линейной интерполяции функции одной переменной 
 .
. , хÎ[х0; хN].
, хÎ[х0; хN].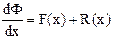 , хÎ[ х0; хN],
, хÎ[ х0; хN], , для всех i=1…N
, для всех i=1…N для всех i=1…N
для всех i=1…N


 , определенной на плоской сетке, содержащей треугольные конечные элементы.
, определенной на плоской сетке, содержащей треугольные конечные элементы.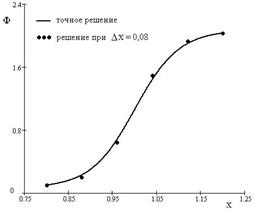

 ,
,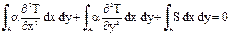

 ,
,