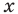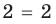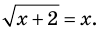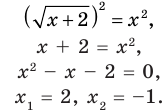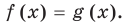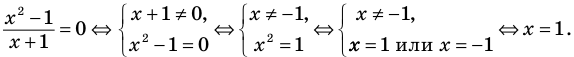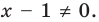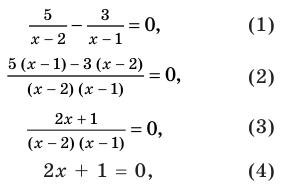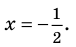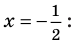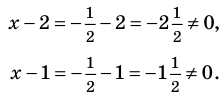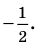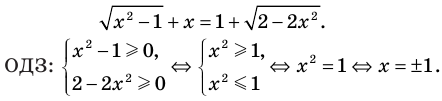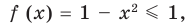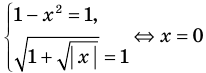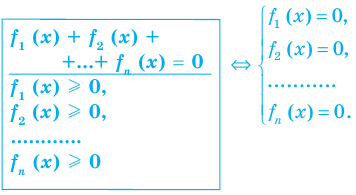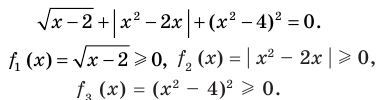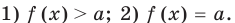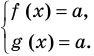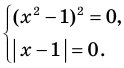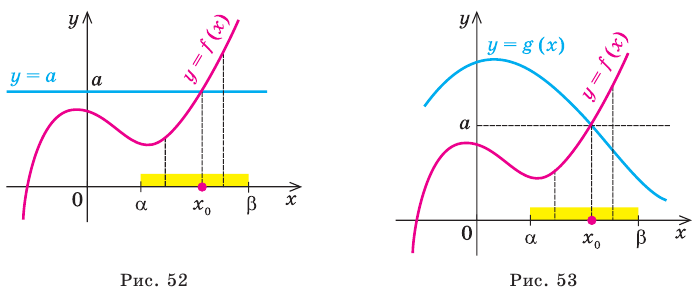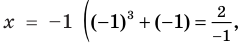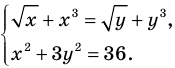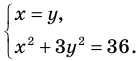Содержание:
- Уравнения
- Уравнения-следствия и равносильные преобразования уравнений
- Понятие уравнения и его корней
- Область допустимых значений (ОДЗ) уравнения
- Методы решения уравнений
- Уравнения-следствия
- Равносильные уравнения
- Причины появления посторонних корней и потери корней при решении уравнений
- Применение свойств функций к решению уравнений
- Конечная ОДЗ
- Оценка левой и правой частей уравнения
- Использование возрастания и убывания функций к решению уравнений
- Квадратные уравнения (способы решения)
- Уравнения с одной переменной
- Определение уравнения. Корни уравнения
- Пример 1.
- Пример 2.
- Пример 3.
- Равносильность уравнений
- Линейные уравнения
- Пример 1.
- Пример 2.
- Квадратные уравнения
- Пример 1.
- Пример 2.
- Пример 3.
- Рациональные уравнения
- Пример:
- Решение уравнения р(х) = 0 методом разложения его левой части на множители
- Пример 1.
- Пример 2.
- Решение уравнений методом введения новой переменной
- Пример 1.
- Пример 2.
- Биквадратные уравнения
- Пример:
- Решение задач с помощью составления уравнений
- Иррациональные уравнения
- Пример 1.
- Пример 2.
- Пример 3.
- Показательные уравнения
- Пример 1.
- Пример 2.
- Пример 3.
- Логарифмические уравнения
- Пример 1.
- Пример 2.
- Пример 3.
- Примеры решения показательно-логарифмических уравнений
- Пример 1.
- Пример 2.
- Пример 3.
- 💡 Видео
Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Уравнения
Уравнения-следствия и равносильные преобразования уравнений
1. Понятие уравнения и его корней
Определение:
Равенство с переменной называется уравнением. В общем виде уравнение с одной переменной
Под этой краткой записью понимают математическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны
Пример:
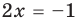
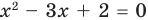
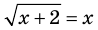
Корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство.
Решить уравнение — значит найти все его корни или доказать, что их нет
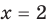
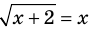
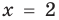
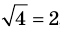
2. Область допустимых значений (ОДЗ)
Областью допустимых значений (или областью определения) уравнения называется общая область определения для функций 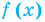
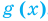
Для уравнения 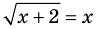
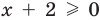
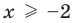
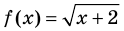

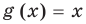
3. Уравнения-следствия
Если каждый корень первого уравнения является корнем второго, то второе уравнение называется следствием первого уравнения.
Если из правильности первого равенства следует правильность каждого последующего, то получаем уравнения-следствия.
При использовании уравнений-следствий не происходит потери корней исходного уравнения, но возможно появление посторонних корней. Поэтому при использовании уравнений-следствий проверка полученных корней подстановкой их в исходное уравнение является составной частью решения.
Пример:
Решение:
► Возведем обе части уравнения в квадрат:
Проверка, 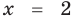
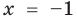
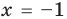
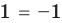
4. Равносильные уравнения
Определение:
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни.
То есть каждый корень первого уравнения является корнем второго уравнения и, наоборот, каждый корень второго уравнения является корнем первого. (Схема решения уравнений с помощью равносильных преобразований приведена в пункте 5 этой таблицы)
Простейшие теоремы
- Если из одной части уравнения перенести в другую слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве)
- Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получим уравнение, равносильное заданному (на ОДЗ заданного уравнения)
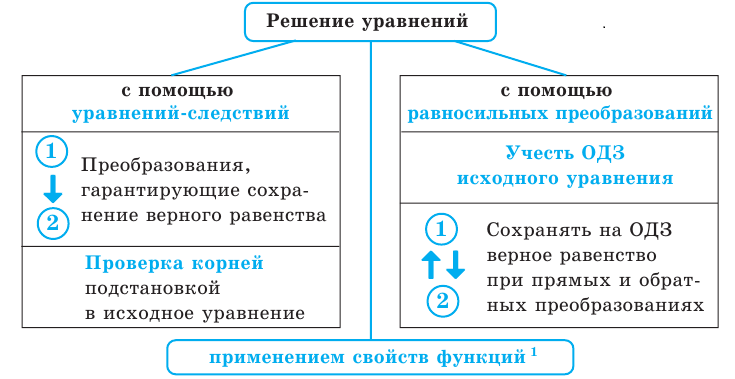
5. Схема поиска плана решения уравнений



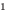
Объяснение и обоснование:
Понятие уравнения и его корней
Уравнение в математике чаще всего понимают как аналитическую запись задачи о нахождении значений аргумента, при которых значения двух данных функций равны. Поэтому в общем виде уравнения с одной переменной 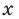
Часто уравнения определяют короче — как равенство с переменной.
Напомним, что корнем (или решением) уравнения с одной переменной называется значение переменной, при подстановке которого в уравнение получается верное равенство. Решить уравнение — значит найти все его корни или доказать, что их нет.
Например, уравнение 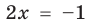
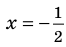
а уравнение 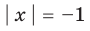
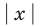
Область допустимых значений (ОДЗ) уравнения
Если задано уравнение 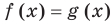
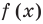
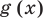
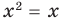
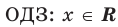
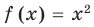
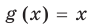
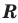
Понятно, что каждый корень данного уравнения принадлежит как области определения функции 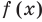
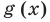
Например, в уравнении 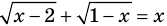
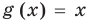
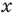
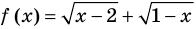
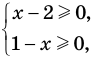
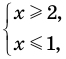
Заметим, что нахождение ОДЗ данного уравнения может быть полезным для его решения, но не всегда является обязательным элементом решения уравнения.
Методы решения уравнений
Для решения уравнений используют методы точного и приближенного решений. А именно, для точного решения уравнений в курсе математики 5-6 классов использовались зависимости между компонентами и результатами действий и свойства числовых равенств; в курсе алгебры 7-9 классов — равносильные преобразования уравнений, а для приближенного решения уравнений — графический метод.
Графический метод решения уравнений не дает высокой точности нахождения корней уравнения, и с его помощью чаще всего можно получить только грубые приближения корней. Иногда удобно графически определить количество корней уравнения или найти границы, в которых находятся эти корни. В некоторых случаях можно графически доказать, что уравнение не имеет корней. По указанным причинам в школьном курсе алгебры и начал анализа под требованием «решить уравнение» понимается требование «используя методы точного решения, найти корни данного уравнения». Приближенными методами решения уравнений можно пользоваться только тогда, когда об этом говорится в условии задачи (например, если ставится задача решить уравнение графически).
В основном при решении уравнений разных видов нам придется применять один из двух методов решения. Первый из них состоит в том, что данное уравнение заменяется более простым уравнением, имеющим те же корни,— равносильным уравнением. В свою очередь, полученное уравнение заменяется еще более простым, равносильным ему, и т. д. В результате получаем простейшее уравнение, которое равносильно заданному и корни которого легко находятся. Эти корни и только они являются корнями данного уравнения.
Второй метод решения уравнений состоит в том, что данное уравнение заменяется более простым уравнением, среди корней которого находятся все корни данного, то есть так называемым уравнением-следствием. В свою очередь, полученное уравнение заменяется еще более простым уравнением-следствием, и так далее до тех пор, пока не получим простейшее уравнение, корни которого легко находятся. Тогда все корни данного уравнения находятся среди корней последнего уравнения. Поэтому, чтобы найти корни данного уравнения, достаточно корни последнего уравнения подставить в данное и с помощью такой проверки получить корни данного уравнения (и исключить так называемые посторонние корни — те корни последнего уравнения, которые не удовлетворяют заданному).
В следующем пункте будет также показано применение свойств функций к решению уравнений определенного вида.
Уравнения-следствия
Рассмотрим более детально, как можно решать уравнения с помощью уравнений-следствий. При решении уравнений главное — не потерять корни данного уравнения, и поэтому в первую очередь мы должны следить за тем, чтобы каждый корень исходного уравнения оставался корнем следующего. Фактически это и является определением уравнения-следствия:
в том случае, когда каждый корень первого уравнения является корнем второго, второе уравнение называется следствием первого.
Это определение позволяет обосновать такой ориентир: для получения уравнения-следствия достаточно рассмотреть данное уравнение как верное числовое равенство и гарантировать (то есть иметь возможность обосновать), что каждое следующее уравнение мы можем получить как верное числовое равенство.
Действительно, если придерживаться этого ориентира, то каждый корень первого уравнения обращает это уравнение в верное числовое равенство, но тогда и второе уравнение будет верным числовым равенством, то есть рассматриваемое значение переменной является корнем и второго уравнения, а это и означает, что второе уравнение является следствием первого.
Применим приведенный ориентир к уравнению 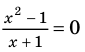
Если правильно то, что дробь равна нулю, то обязательно ее числитель равен нулю. Таким образом, из заданного уравнения получаем уравнение-следствие 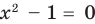
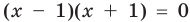
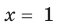
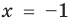
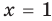
Это происходит поэтому, что, используя уравнения-следствия, мы гарантируем только то, что корни заданного уравнения не теряются (каждый корень первого уравнения является корнем второго). Но второе уравнение, кроме корней первого уравнения, имеет еще и другой корень, который не является корнем первого уравнения. Для первого уравнения этот корень является посторонним, и, чтобы его отсеять, выполняется проверка подстановкой корней в исходное уравнение. (Более полно причины появления посторонних корней рассмотрены в таблице 9.) Таким образом, чтобы правильно применять уравнения-следствия для решения уравнений, необходимо помнить еще один ориентир: при использовании уравнений-следствий возможно появление посторонних корней, и поэтому проверка подстановкой корней в исходное уравнение является составной частью решения.
Схема применения этих ориентиров дана в таблице 8. В пункте 3 этой таблицы приведено решение уравнения
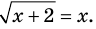
Для решения этого уравнения с помощью уравнений-следствий достаточно данное уравнение рассмотреть как верное числовое равенство и учесть, что в случае когда два числа равны, то и их квадраты также будут равны:
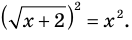
То есть мы гарантируем, что если равенство (1) верно, то и равенство (2) также будет верным, а это и означает (как было показано выше), что уравнение (2) является следствием уравнения (1). Если мы хотя бы один раз использовали уравнения-следствия (а не равносильные преобразования), то можем получить посторонние корни, и тогда в решение обязательно входит проверка полученных корней подстановкой их в заданное уравнение.
Замечание. Переход от данного уравнения к уравнению-следствию можно обозначить специальным значком 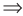
Равносильные уравнения
С понятием равносильности вы знакомы еще из курса алгебры 7 класса, где равносильными назывались те уравнения, которые имели одни и те же корни. Заметим, что равносильными считались и такие два уравнения, которые не имели корней. Формально будем считать, что и в этом случае уравнения имеют одни и те же корни, поскольку ответы к таким уравнениям одинаковы: «уравнения не имеют корней» (точнее: одинаковыми являются множества корней таких уравнений — они оба пустые, что обозначается символом 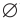
В курсе алгебры и начал анализа мы будем рассматривать более общее понятие равносильности, а именно: равносильность на определенном множестве.
Два уравнения называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же корни, то есть каждый корень первого уравнения является корнем второго и, наоборот, каждый корень второго уравнения является корнем первого.
Для уравнений, заданных на множестве всех действительных чисел (например, для линейных), мы можем однозначно дать ответ на вопрос: «Равносильны ли данные уравнения?» Например, уравнения 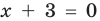
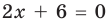
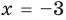
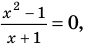
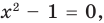
то, как было показано выше, уравнение (3) имеет единственный корень 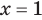
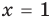
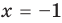
всех действительных чисел эти уравнения не являются равносильными, поскольку у уравнения (4) есть корень 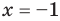
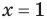
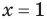
Укажем, что множество, на котором рассматривается равносильность уравнений, как правило, не задается искусственно (как в последнем случае), а чаще всего таким множеством является ОДЗ исходного уравнения. Договоримся, что далее
все равносильные преобразования уравнений (а также неравенств и систем уравнений и неравенств) мы будем выполнять на ОДЗ исходного уравнения (неравенства или системы).
Отметим, что в том случае, когда ОДЗ заданного уравнения является множество всех действительных чисел, мы не всегда будем ее записывать (как не записывали ОДЗ при решении линейных или квадратных уравнений). И в других случаях главное — не записать ОДЗ в решение уравнения, а реально учесть ее при выполнении равносильных преобразований данного уравнения.
Например, для уравнения 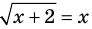
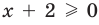

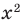
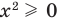
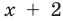


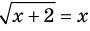
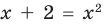
Для выполнения равносильных преобразований попробуем выделить общие ориентиры, аналогичные соответствующим ориентирам получения уравнений-следствий. Как указывалось выше, выполняя равносильные преобразования уравнений, необходимо учесть ОДЗ данного уравнения — это и есть первый ориентир для выполнения равносильных преобразований уравнений. По определению равносильности уравнений необходимо гарантировать, чтобы каждый корень первого уравнения был корнем второго и, наоборот, каждый корень второго уравнения был корнем первого. Для первой части этого требования мы уже выделили общий ориентир: достаточно гарантировать сохранение правильности равенства при переходе от первого уравнения ко второму.
Но тогда, чтобы выполнить вторую часть этого требования, достаточно второе уравнение рассмотреть как верное равенство (то есть взять такое значение переменной, которое является корнем второго уравнения) и гарантировать, что при переходе к первому верное равенство сохраняется (этот корень остается и корнем первого уравнения). Фактически из определения равносильности уравнений получаем, что каждое из равносильных уравнений является следствием другого уравнения). Таким образом, при выполнении равносильных преобразований мы должны гарантировать сохранение правильности равенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях — это и является вторым ориентиром для решения уравнений с помощью равносильных преобразований. (Соответствующие ориентиры схематически представлены в пункте 5 табл. 8.)
Например, чтобы решить с помощью равносильных преобразований уравнение 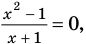
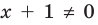
Запись решения в этом случае может быть такой:
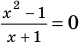
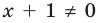
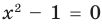
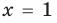
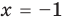
Для выполнения равносильных преобразований уравнений можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности уравнений обобщим также формулировки простейших теорем о равносильности, известных из курса алгебры 7 класса.
Теорема 1. Если из одной части уравнения перенести в другую часть слагаемые с противоположным знаком, то получим уравнение, равносильное заданному (на любом множестве).
Теорема 2. Если обе части уравнения умножить или разделить на одно и то же число, не равное нулю (или на одну и ту же функцию, которая определена и не равна нулю на ОДЗ заданного уравнения), то получаем уравнение, равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований данного уравнения.
Замечание. Для обозначения перехода от данного уравнения к равносильному ему уравнению можно применять специальный значок 
Пример №423
Решите уравнение 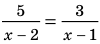
Решение:
► ОДЗ: 
На этой ОДЗ данное уравнение равносильно уравнениям:
то есть
Учтем ОДЗ. При
Таким образом, 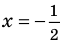
Ответ:
Используем равносильные преобразования для решения данного уравнения. Для этого необходимо учесть ОДЗ, поэтому зафиксируем ее ограничения в начале решения.
Укажем, что в уравнениях ограничения ОДЗ можно только зафиксировать, но не решать, а в конце проверить, выполняются ли эти ограничения для найденных корней.
При переносе члена данного уравнения из одной части уравнения в другую с противоположным знаком получаем уравнение (1), равносильное заданному.
Приводя к общему знаменателю, раскрывая скобки и приводя подобные члены, снова получаем верное равенство и можем обосновать, что при выполнении обратных действий равенство также не нарушается, таким образом, полученные уравнения (1)-(3) равносильны заданному (на его ОДЗ).
Дробь равна нулю тогда и только тогда, когда числитель дроби равен нулю, а знаменатель не равен нулю. Но второе условие уже учтено в ограничениях ОДЗ, таким образом, получаем уравнение (4), равносильное заданному уравнению на его ОДЗ. Поскольку все преобразования были равносильными только с учетом ОДЗ, то мы должны проверить, удовлетворяет ли полученное число ограничениям ОДЗ.
Причины появления посторонних корней и потери корней при решении уравнений
Наиболее типичные случаи появления посторонних корней и потери корней приведены в таблице 9. Там же указано, как в каждом из этих случаев получить правильное (или полное) решение.
Применение свойств функций к решению уравнений
1. Конечная ОДЗ
Если область допустимых значений (ОДЗ) уравнения (неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения
Пример:
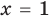
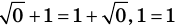
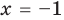
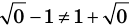
2. Оценка левой и правой частей уравнения
Если надо решить уравнение вида 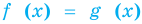


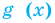
Пример:
►
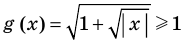
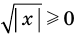
Итак, заданное уравнение равносильно системе
Сумма нескольких неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю
Пример:
►
Итак, заданное уравнение равносильно системе
Из первого уравнения получаем 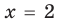
3. Использование возрастания и убывания функций
Схема решения уравнения
1. Подбираем один или несколько корней уравнения.
2. Доказываем, что других корней это уравнение не имеет (используя теоремы о корнях уравнения или оценку левой и правой частей уравнения)
Теоремы о корнях уравнения
Если в уравнении 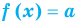
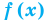
Пример:
Уравнение 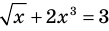
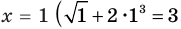
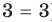
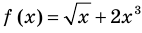
Если в уравнении 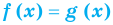
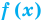
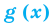
Пример:
Уравнение 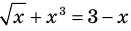
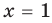
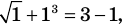
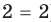
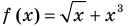

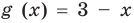
Объяснение и обоснование:
Конечная ОДЗ
Напомним, что в случае, когда дано уравнение 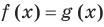
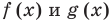
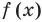
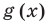
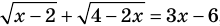
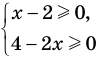
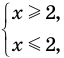


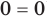


Рассмотренный пример позволяет выделить ориентир для решения аналогичных уравнений:
если ОДЗ уравнения (а также неравенства или системы) состоит из конечного числа значений, то для решения достаточно проверить все эти значения.
Замечание. В том случае, когда ОДЗ — пустое множество (не содержит ни одного числа), мы можем сразу дать ответ, что данное уравнение не имеет корней.
Например, если необходимо решить уравнение 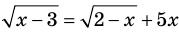
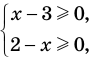
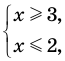
Оценка левой и правой частей уравнения
Некоторые уравнения можно решить с помощью оценки левой и правой частей уравнения.
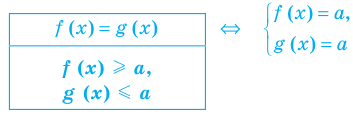
Пусть дано уравнение 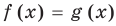
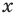
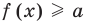
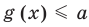
Рассмотрим два случая:
Если 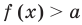
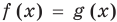
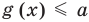
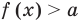
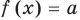
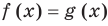
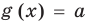
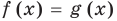
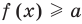
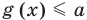
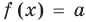
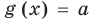
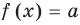
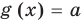
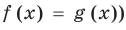
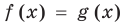
Коротко это можно записать так:
Пример использования такого приема решения уравнений приведен в пункте 2 таблицы 10.
Аналогично предыдущим рассуждениям обосновывается и ориентир по решению уравнения 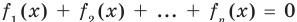
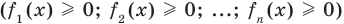
Если предположить, что 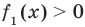

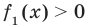
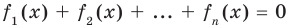
Например, чтобы решить уравнение 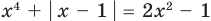
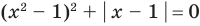
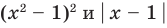
Из второго уравнения получаем 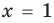
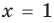
Использование возрастания и убывания функций к решению уравнений
Использование возрастания и убывания функций к решению уравнений опирается на такое свойство: возрастающая или убывающая функция принимает каждое свое значение только в одной точке ее области определения.
Полезно помнить специальные теоремы о корнях уравнения.
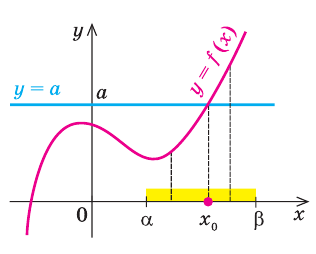
Теорема 1. Если в уравнении 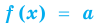
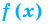
Графически утверждение теоремы проиллюстрировано на рисунке 52. Прямая 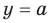
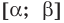
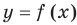
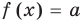
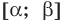
• Если на промежутке 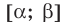
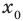
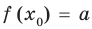
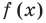
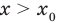
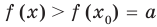
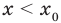
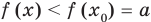
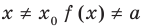
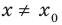
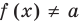
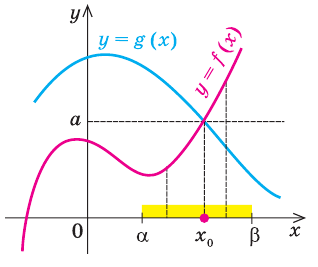
Теорема 2. Если в уравнении 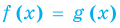
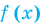
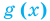
Графически утверждение теоремы проиллюстрировано на рисунке 53.
• Если на промежутке 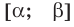
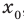
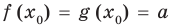
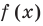
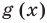
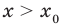
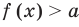
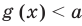
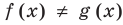
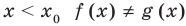
Каждая из этих теорем утверждает, что в рассмотренном промежутке данное уравнение может иметь не более чем один корень, то есть или это уравнение совсем не имеет корней, или оно имеет единственный корень. Если нам удалось подобрать один корень такого уравнения, то других корней в заданном промежутке уравнение не имеет.
Например, чтобы решить уравнение 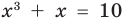
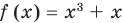

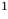
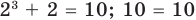
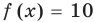
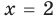
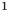

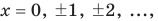
Заметим, что каждая из этих теорем гарантирует единственность корня уравнения (если он есть) только на промежутке возрастания (или убывания) соответствующей функции. Если функция имеет несколько промежутков возрастания и убывания, то приходится рассматривать каждый из них отдельно.
Пример:
Решим с помощью теоремы 2 уравнение 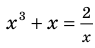
► Сначала следует учесть его ОДЗ: 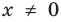
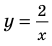
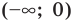
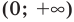
1) При 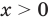
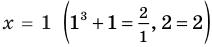
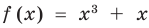

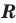
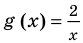

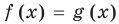
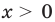
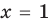
2) При 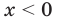
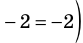
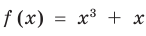
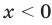
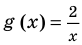
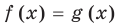
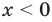
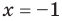
Примеры решения задач:
Пример №424
Решите уравнение 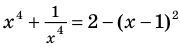
Решение:
► ОДЗ: 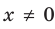
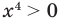
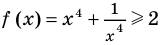
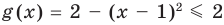
Таким образом, данное уравнение равносильно системе 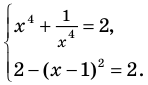


Если раскрыть скобки и привести обе части уравнения к общему знаменателю, то для нахождения корней полученного уравнения придется решать полное уравнение восьмой степени, все корни которого мы не сможем найти.
Попытаемся оценить области значений функций, стоящих в левой и правой частях уравнения. Поскольку на ОДЗ 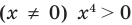
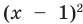
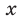
Пример №425
Решите систему уравнений
Решение:
► ОДЗ: 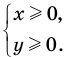
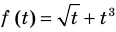
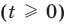
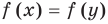
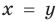
Подставляя 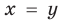
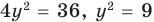
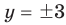

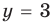
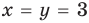
Иногда свойства функций удается применить при решении систем уравнений. Если заметить, что в левой и правой частях первого уравнения заданной системы стоят значения одной и той же функции, которая является возрастающей (как сумма двух возрастающих функций), то равенство 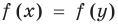
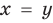
Замечание. Утверждение, обоснованное в комментарии к задаче 2, может быть использовано при решении аналогичных задач. Коротко его можно сформулировать так: если функция 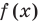
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Метод математической индукции
- Система координат в пространстве
- Иррациональные числа
- Действительные числа
- Интеграл и его применение
- Первообразная и интегра
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:10 класс, 5 урок, Модуль действительного числаСкачать

Квадратные уравнения (способы решения)
Разделы: Математика
Необходимость решать уравнения не только первой, но и второй степени ещё в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
Квадратные уравнения умели решать около 2000 лет до нашей эры в Вавилоне. Применяя современную алгебраическую запись, можно сказать, что в их книгописных текстах встречаются, кроме неполных, и такие, как полные квадратные уравнения.
Определение
Уравнение вида ax 2 + bx + c = 0, где a, b, c — действительные числа, причем a ≠ 0, называют квадратным уравнением.
Если a = 1 , то квадратное уравнение называют приведенным; если a ≠ 1, то неприведенным .
Числа a, b, c носят следующие названия: a — первый коэффициент, b — второй коэффициент, c — свободный член.
| Корни уравнения ax 2 + bx + c = 0 находят по формуле |  |
Выражение D = b 2 — 4ac называют дискриминантом квадратного уравнения.
- если D 0, то уравнение имеет два действительных корня.
В случае, когда D = 0, иногда говорят, что квадратное уравнение имеет два одинаковых корня.
Формулы
Полное квадратное уравнение
Неполные квадратные уравнения
Если в квадратном уравнении ax 2 + bx + c = 0 второй коэффициент b или свободный член c равен нулю, то квадратное уравнение называется неполным.
Неполные уравнения выделяют потому, что для отыскания их корней можно не пользоваться формулой корней квадратного уравнения — проще решить уравнение методом разложения его левой части на множители.
Способы решения неполных квадратных уравнений:
Решение неполного квадратного уравнения
Квадратные уравнения с комплексными переменными
Сначала рассмотрим простейшее квадратное уравнение z 2 = a, где a-заданное число, а z-неизвестное. На множестве действительных чисел это уравнение:
- имеет один корень z = 0, если а = 0;
- имеет два действительных корня z1, 2 = ±√a
- Не имеет действительных корней, если a 2 + x + 1 = 0.
Решим уравнение. Для этого построим два графика y = x 2 ; y = x + 1.
y = x 2 , квадратичная функция, график парабола.
y = x + 1, линейная функция, график прямая.
Графики пересекаются в двух точках, уравнение имеет два корня.
Ответ: x ≈ -0,6; x ≈ 2,6.
Решение задач с помощью квадратных уравнений
| Процессы | Скорость км/ч | Время ч. | Расстояние км. |
|---|---|---|---|
| Вверх по реке | 10 — x | 35 / (10 — x) | 35 |
| Вверх по протоку | 10 — x + 1 | 18 / (10 — x + 1) | 18 |
| V течения | x | ||
| V притока | x + 1 |
Зная, что скорость в стоячей воде равна 10 км/ч, составим уравнение.
Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Уравнения с одной переменной
Уравнением с одной переменной — это равенство, содержащее только одну переменную. Корнем (или решением) уравнения называется такое значение переменной, при котором уравнение превращается в верное числовое равенство.
Содержание:
Определение уравнения. Корни уравнения
Равенство с переменной f(x) = g (х) называют уравнением с одной переменной х, если поставлена задача найти все те же значения х, при которых равенство с переменной обращается в верное числовое равенство. Всякое значение переменной, при котором выражения /(х) и g(x) принимают равные числовые значения, называют корнем уравнения.
Решить уравнение — это значит найти все его корни или доказать, что их нет.
Пример 1.
Уравнение 3 + х = 7 имеет единственный корень 4, так как при этом и только при этом значении переменной равенство 3 + х = 7 является верным.
Пример 2.
Уравнение (х — 1)(х — 2) = 0 имеет два корня: 1 и 2.
Пример 3.
Уравнение 
Заметим, что можно говорить и о мнимых корнях уравнений. Так, уравнение 

Равносильность уравнений
Уравнения, имеющие одни и те же корни, называют равносильными. Равносильными считаются и уравнения, каждое из которых не имеет корней.
Например, уравнения х + 2 = 5 и х + 5 = 8 равносильны, так как каждое из них имеет единственный корень — число 3. Равносильны и уравнения 
Уравнения 
В процессе решения уравнения его стараются заменить более простым, но равносильным данному. Поэтому важно знать, при каких преобразованиях данное уравнение переходит в равносильное ему уравнение.
Теорема 1.
Если в уравнении какое-нибудь слагаемое перенести из одной части в другую, изменив его знак, то получится уравнение, равносильное данному.
Например, уравнение 
Теорема 2.
Если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Например, уравнение 

Линейные уравнения
Линейным уравнением с одной переменной х называют уравнение вида
где 


Для линейного уравнения 
1) 

2) 

3) 

Многие уравнения в результате преобразований сводятся к линейным.
Пример 1.
Решить уравнение
Решение:
По теореме 1 (см. п. 135), данное уравнение равносильно уравнению 


Пример 2.
Решение:
Это уравнение сводится к линейному уравнению. Умножив обе части уравнения на 12 (наименьшее общее кратное знаменателей 3, 4, 6,12), получим
Квадратные уравнения
где 







Выражение 
В случае, когда D = О, иногда говорят, что квадратное уравнение имеет два одинаковых корня.
Используя обозначение 


Формула (3) особенно удобна, если 

Пример 1.
Решение:
Здесь 
Так как 
Итак, 

Пример 2.
Решить уравнение
Решение:
Здесь 

Пример 3.
Решить уравнение
Решение:
Здесь 
Рациональные уравнения
Уравнение f(x) = g(x) называют рациональным, если f(x) и g(x) — рациональные вьфажения. При этом если f(x) и g(x) — целые выражения, то уравнение называют целым; если же хотя бы одно из выражений f(х), g(x) является дробным, то рациональное уравнение f(x) = g(x) называют дробным.
Например, целыми являются линейные (см. п. 136), квадратные (см. п. 137) уравнения.
Чтобы решить рациональное уравнение, нужно:
1) найти общий знаменатель всех имеющихся дробей;
2) заменить данное уравнение целым, умножив обе его части на общий знаменатель;
3) решить полученное целое уравнение;
4) исключить из его корней те, которые обращают в нуль общий знаменатель.
Пример:
Решение:
Общим знаменателем имеющихся дробей является 2х(2 — х). Найдя дополнительные множители для каждой дроби, освободимся от знаменателей. Имеем:
Из уравнения 


Решение уравнения р(х) = 0 методом разложения его левой части на множители
Суть этого метода состоит в следующем. Пусть нужно решить уравнение р(х) = 0, где р(х) — многочлен степени 







Значит, 
Верно и обратное: если 



Итак, если 



Пример 1.
Решить уравнение
Решение:
Разложим на множители левую часть уравнения. Имеем 
Значит, либо х + 2 = 0, либо 
Метод разложения на множители применим к любым уравнениям вида р(х) = 0, где р(х) необязательно многочлен. Пусть 



Пример 2.
Решить уравнение
Решение:
Имеем 





Но х = -3 не удовлетворяет исходному уравнению, так как при этом значении не определено выражение 
Итак, уравнение имеет два корня: 3; 0.
Решение уравнений методом введения новой переменной
Суть этого метода поясним на примерах.
Пример 1.
Решение:
Положив 
откуда находим 
Первое квадратное уравнение не имеет действительных корней, так как его дискриминант отрицателен.
Из второго квадратного уравнения находим 
Пример 2.
Решение:
Положим 
и уравнение примет вид
Решив это уравнение (см. п. 145), получим
Но 
Из первого уравнения находим 



Биквадратные уравнения
Биквадратным уравнением называют уравнение вида
Биквадратное уравнение решается методом введения новой переменной: положив 
Пример:
Решить уравнение 
Решение:
Положив 




Решение задач с помощью составления уравнений
С помощью уравнений решаются многочисленные задачи, к которым приводят самые разнообразные вопросы физики, механики, экономики и т. д. Прежде всего напомним общий порядок решения задач с помощью уравнений.
1) Вводят переменные, т. е. буквами х, у, z обозначают неизвестные величины, которые либо требуется найти в задаче, либо они необходимы для отыскания искомых величин.
2) С помощью введенных переменных и данных в задаче чисел и их соотношений составляют систему уравнений (или одно уравнение).
3) Решают составленную систему уравнений (или уравнение) и из полученных решений отбирают те, которые подходят по смыслу задачи.
4) Если буквами х, у, z обозначили не искомые величины, то с помощью полученных решений находят ответ на вопрос задачи.
Задача 1.
Для перевозки 60 т груза из одного места в другое затребовали некоторое количество машин. Ввиду неисправности дороги на каждую машину пришлось грузить на 0,5 т меньше, чем предполагалось, поэтому дополнительно потребовались 4 машины. Какое количество машин было затребовано первоначально?
Решение: Обозначим через х количество машин, затребованных первоначально. Тогда на самом деле было вызвано (х + 4) машин. Так как надо было перевезти 60 т груза, то предполагалось, что на одну машину будут грузить 

Это уравнение имеет два корня: х = -24, х = 20. Ясно, что по смыслу задачи значение х = —24 не подходит. Таким образом, первоначально было затребовано 20 машин.
Задача 2.
Моторная лодка, движущаяся со скоростью 20 км/ч, прошла расстояние между двумя пунктами по реке туда и обратно без остановок за 6 ч 15 мин. Расстояние между пунктами равно 60 км. Найти скорость течения реки.
Решение:
Пусть х км/ч — скорость течения реки. Тогда лодка, собственная скорость которой 20 км/ч, идет по течению со скоростью (20 + х) км/ч, а против течения — со скоростью (20 — х) км/ч. Время, за которое лодка пройдет путь между пунктами по течению, составит 


решив которое, находим два корня: х = 4, х = -4. Ясно, что значение х = -4 не подходит по смыслу задачи. Итак, скорость течения реки равна 4 км/ч.
Задача 3.
Найти двузначное число, зная, что цифра его единиц на 2 больше цифры десятков и что произведение искомого числа на сумму его цифр равно 144.
Решение:
Напомним, что любое двузначное число может быть записано в виде 10х + у, где х — цифра десятков, а у — цифра единиц. Согласно условию, если х — цифра десятков, то цифра единиц равна х + 2 и мы получаем
Решив это уравнение, найдем
Второй корень не подходит по смыслу задачи.
Итак, цифра десятков равна 2, цифра единиц равна 4; значит, искомое число равно 24.
Задача 4.
Двое рабочих, работая вместе, выполнили некоторую работу за 6 ч. Первый из них, работая отдельно, может выполнить всю работу на 5 ч скорее, чем второй рабочий, если последний будет работать отдельно. За сколько часов каждый из них, работая отдельно, может выполнить всю работу?
Решение:
Производительность труда, т. е. часть работы, выполняемая в единицу времени (обозначим ее через А), и время, необходимое для выполнения всей работы (обозначим его через t), — взаимно обратные величины, т. е. At = 1. Поэтому если обозначить через х ч время, необходимое для выполнения всей работы первому рабочему, а через (х + 5) ч — второму, то часть работы, выполняемая первым рабочим за 1 ч, равна 



решив которое, найдем х = 10.
Итак, первый рабочий может выполнить всю работу за 10 ч, а второй — за 15 ч.
Задача 5.
Из сосуда емкостью 54 л, наполненного кислотой, вылили несколько литров и долили сосуд водой, потом опять вылили столько же литров смеси. Тогда в оставшейся в сосуде смеси оказалось 24 л чистой кислоты. Сколько кислоты вылили в первый раз?
Решение:
Пусть в первый раз было вылито х л кислоты. Тогда в сосуде осталось (54 — х) л кислоты. Долив сосуд водой, получили 54 л смеси, в которой растворилось (54 — х) л кислоты. Значит, в 1 л смеси содержится 


за два раза вылито 54 — 24 = 30 л кислоты. В результате приходим к уравнению
Решив это уравнение, найдем два корня: 

Итак, в первый раз было вылито 18 л кислоты.
Задача 6.
Имеется кусок сплава меди с оловом массой 12 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к этому куску, чтобы получившийся новый сплав содержал 40% меди?
Решение:
Пусть масса добавленного олова составляет х кг. Тогда получится сплав массой (12 + х) кг, содержащий 40% меди. Значит, в новом сплаве имеется 0,4(12 + х) кг меди. Исходный сплав массой 12 кг содержал 45% меди, т. е. меди в нем было 
Решив это уравнение, получим х = 1,5. Таким образом, к исходному сплаву надо добавить 1,5 кг олова.
Задача 7.
Имеется сталь двух сортов с содержанием никеля 5% и 40%. Сколько стали того и другого сорта надо взять, чтобы после переплавки получить 140 т стали с содержанием никеля 30% ?
Решение:
Пусть масса стали первого сорта равна х т, тогда стали второго сорта надо взять (140 — х) т. Содержание никеля в стали первого сорта составляет 5%; значит, в х т стали первого сорта содержится 0,05л; т никеля. Содержание никеля в стали второго сорта составляет 40%; значит, в (140 — х) т стеши второго сорта содержится 0,4 (140 — х) т никеля. По условию после соединения взятых двух сортов должно получиться 140 т стали с 30% -ным содержанием никеля, т. е. после переплавки в полученной стали должно быть 0,3 * 140 т никеля. Но это количество никеля складывается из 0,05л; т, содержащихся в стали первого сорта, и из 0,4 (140 — х) т, содержащихся в стали второго сорта. Таким образом, приходим к уравнению
0,05х + 0,4 (140 — х) = 0,3 * 140,
из которого находим х = 40. Следовательно, надо взять 40 т стали с 5% -ным и 100 т стали с 40% -ным содержанием никеля.
Иррациональные уравнения
Иррациональным называют уравнение, в котором переменная содержится под знаком радикала или под знаком возведения в дробную степень. Например, иррациональными являются уравнения
Используются два основных метода решения иррациональных уравнений:
1) метод возведения обеих частей уравнения в одну и ту же степень;
2) метод введения новых переменных (см. п. 147).
Метод возведения обеих частей уравнения в одну
и ту же степень состоит в следующем:
а) преобразуют заданное иррациональное уравнение к виду
б) возводят обе части полученного уравнения в п-ю степень:
в) учитывая, что 
г) решают уравнение и, в случае четного п, делают проверку, так как возведение обеих частей уравнения в одну и ту же четную степень может привести к появлению посторонних корней (см. п. 142). Эта проверка чаще всего осуществляется с помощью подстановки найденных значений переменной в исходное уравнение.
Пример 1.
Решить уравнение
Решение:
Возведем обе части уравнения в шестую степень; получим х — 3 = 64, откуда х = 67.
Проверка:
Подставив 67 вместо х в данное уравнение, получим 
Ответ: 67.
Пример 2.
Решение:
Преобразуем уравнение к виду
и возведем обе части его в квадрат. Получим
Еще раз возведем обе части уравнения в квадрат:
откуда
Проверка:
1) При х = 5 имеем

Таким образом, х = 5 является корнем заданного уравнения.
2) При х = 197 имеем 
Ответ: 5.
Пример 3.
Решение:
Применим метод введения новой переменной.
Положим 

Теперь задача свелась к решению совокупности уравнений
Возведя обе части уравнения 
Уравнение 
Ответ: 34.
Показательные уравнения
Показательное уравнение вида
где 
Имеются два основных метода решения показательных уравнений:
1) метод уравнивания показателей, т. е. преобразование заданного уравнения к виду 
2) метод введения новой переменной.
Пример 1.
Решить уравнение
Решение:
Данное уравнение равносильно уравнению 


Пример 2.
Решение:
Приведем все степени к одному основанию 




Пример 3.
Решить уравнение
Решение:
Применим метод введения новой переменной. Так как 
Введем новую переменную, положив 


Из первого уравнения находим х = 2. Второе уравнение не имеет корней, так как 
Ответ: 2.
Логарифмические уравнения
Чтобы решить логарифмическое уравнение вида
где 
1) решить уравнение f(x) = g(x);
2) из найденных корней отобрать те, которые удовлетворяют неравенствам f(x) > 0 и g(x) > 0; остальные корни уравнения f(x) = g(x) являются посторонними для уравнения (1).
Имеются два основных метода решения логарифмических уравнений:
1) метод, заключающийся в преобразовании уравнения к виду 
2) метод введения новой переменной.
Пример 1.
Решение:
Перейдем от заданного уравнения к уравнению 


Ответ: -3.
Пример 2.
Решение:
Воспользовавшись тем, что сумма логарифмов равна логарифму произведения (см. п. 120), преобразуем уравнение к виду
Из последнего уравнения находим
Осталось сделать проверку. Ее можно выполнить с помощью системы неравенств
Подставив поочередно найденные значения -1 и -5,5 в эти неравенства, убеждаемся, что -1 удовлетворяет всем неравенствам, а -5,5 — нет, например при этом значении не выполняется первое неравенство. Значит, -5,5 — посторонний корень.
Ответ: -1.
Пример 3.
Решение:
Так как 

Введем новую переменную, положив 
Но 

Ответ: 4.
Примеры решения показательно-логарифмических уравнений
Пример 1.
Решение:
Область определения уравнения: х > 0. При этом условии выражения, входящие в обе части уравнения (1), принимают только положительные значения. Прологарифмировав обе части уравнения (1) по основанию 10, получим уравнение
равносильное уравнению (1). Далее имеем
Полагая 




Здесь применен метод логарифмирования, заключающийся в переходе от уравнения f(x) = g(x) к уравнению
Пример 2.

Решение:
Воспользовавшись определением логарифма, преобразуем уравнение (2) к виду
Полагая 

Теперь задача сводится к решению совокупности уравнений
Так как 
если 



Итак, если 






Пример 3.
При каких значениях параметра 
имеет два различных отрицательных корня?
Решение:
Так как уравнение должно иметь два различных действительных корня 
Значит, должно выполняться неравенство
По теореме Виета для заданного уравнения имеем
Так как, по условию, 

В итоге мы приходим к системе неравенств (см. п. 177):
Из первого неравенства системы находим (см. п. 180, 183) 



Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:
Смотрите также дополнительные лекции по предмету «Математика»:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
💡 Видео
Что такое действительные числа? - bezbotvyСкачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА решение примеровСкачать

Алгебра 10 класс (Урок№15 - Действительные числа.)Скачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Решение биквадратных уравнений. 8 класс.Скачать

Уравнения с модулемСкачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Натуральные числа, целые числа, рациональные числа, иррациональные числа и действительные числаСкачать

Схема Горнера. 10 класс.Скачать

ПРОСТЕЙШИЙ способ решения Показательных УравненийСкачать

Комплексные корни квадратного уравненияСкачать

КОМПЛЕКСНЫЕ ЧИСЛА ДЛЯ ЧАЙНИКОВ ЗА 7 МИНУТСкачать

Как решают уравнения в России и США!?Скачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Математика | Решение уравненийСкачать

Найти все действительные решения уравнения с двумя переменнымиСкачать