Что означает константа в уравнении регрессии (8 видео)

Содержание

Что означает константа в уравнении регрессии
Каковы условия интерпретируемости константы в уравнении линейной регрессии?
Интерпретация уравнения регрессии
Интерпретация уравнения регрессии
📹 Видео

Видео:Математика #1 | Корреляция и регрессияСкачать

Что означает константа в уравнении регрессии

41. В чем состоят условия Гаусса-Маркова?

Модель линейна по параметрам (коэффициентам), правильно специфицирована, содержит аддитивный случайный член.
Объясняющая переменная не коррелированна со случайным членом
Математическое ожидание случайного члена равно нулю (E(u_i)=0 для всех i)
Случайный член гомоскедастичен (то есть его значение в каждом наблюдении получено из распределения с постоянной теоретической дисперсией: σ 2 _ui =σ 2 _u для всех i)
Значения случайного члена имеют взаимно независимые распределения (u_i распределен независимо от u_j для всех j≠i).
Случайный член имеет нормальное распределение (необязательное, но часто используемое условие).

42. Какой вывод относительно оцениваемого уравнения регрессии можно сделать из

выполнимости условий Гаусса-Маркова?

МНК-оценка в данном случае является лучшей оценкой в классе линейных.

43. Что произойдет, если по крайней мере одно из условий Гаусса-Маркова не выполняется?

Если не выполняется 1 и 4 условие, то появляется систематическое смещение; если не выполняется 2 и 3 – оценки становятся неэффективными. В обоих случаях модель некорректна.

44. Можно ли проверить выполнение условий Гаусса-Маркова? Если да, то каким образом?

Посмотреть на показатели качества коэффициентов регрессии, а также посмотреть на показатели качества уравнения в целом. Нет интерпретации.

45. На основании чего можно судить о вероятном выполнении или невыполнении условий Гаусса-Маркова?

На основании диаграммы рассеяния, графика остатков. Важно, что случайный член (о котором теорема Гаусса-Маркова) и остатки различны, но их поведение похоже, однако случайный член не наблюдаем, зато остатки легко наблюдаемы. Поэтому мы используем остатки, чтобы судить о свойствах случайного члена.

46. Что означает, что модель линейна по параметрам?

Означает, что модель представляет собой взвешенную сумму параметров, а переменные выступают как веса, иными словами, параметры представлены непосредственно, а не как функции (например, log)

47. Можно ли оценивать методом наименьших квадратов уравнение регрессии без константы?

48. В чем состоит роль константы уравнения регрессии?

Роль константы состоит в отражении любой систематической, но постоянной составляющей в зависимой переменной, которую не учитывают объясняющие переменные, включенные в уравнение регрессии, однако, которая оказывает влияние на исследуемую зависимую переменную. Константа интерпретируется в случае соответствия ее значения здравому смыслу или теоретическим предпосылкам.

49. К чему приводит исключение константы из линейного уравнения регрессии?

Исключение постоянного члена приводит к нарушению одного из условия Гаусса-Маркова (о равенстве нулю мат. ожидания случайного члена)

1. Оценки коэффициентов при переменных искажаются и смещаются

2. t-статистики становятся некорректными

1. За редкими и обоснованными исключениями не следует исключать постоянный член уравнения

2. Не следует полагаться на оценку самого свободного члена

50. В каких случаях исключение константы из уравнения регрессии оправдано?

В том случае если константа незначима в уравнении регрессии.

Исключение постоянного члена всегда должно быть обосновано содержательно экономически

Пример: Анализ затрат

Если постоянные затраты малы, то можно исключить свободный член, получив лишнюю степень свободы

Необоснованное исключение свободного члена приводит к серьезным ошибкам!

51. Что значит, что случайный член регрессии является аддитивным?

Это значит, что случайный член прибавляется к другим составляющим частям регрессии.

52. Зачем используется дополнительное условие нормальности распределения случайного члена?

Если случайный член и нормально распределен, то так же будут распределены и коэффициенты регрессии. Это условие необходимо для проводения проверки гипотез и определять доверительные интервалы для a и b, используя результаты построения регрессии.

53. Можно ли использовать уравнение регрессии, если условие нормальности распределения случайного члена не выполняется?

Если условие нормальности распределения случайного члена не выполняется, то неверно предполагать, что оценки коэффициентов регрессии имеют совместное нормальное распределение, однако при некоторых условиях регулярности на поведение объясняющих переменных в случае роста числа наблюдений оценки коэффициентов регрессии имеют асимптотически нормальное распределение. Следовательно, уравнение регрессии использовать можно (по Магнусу).

54. Какие изменения нужно внести в анализ регрессии, если известно, что предположение о нормальности распределения случайного члена регрессии не является справедливым?

Отказаться от использования тестов. Сами оценки регрессии остаются лучшими.

Видео:Что такое линейная регрессия? Душкин объяснитСкачать

Каковы условия интерпретируемости константы в уравнении линейной регрессии?

Константу можно интерпретировать, когда она значима и когда это имеет экономический смысл. Второе условие выполняется для регрессий временного ряда (показывает значение зависимой переменной в базовый период).Формально говоря, она показывает прогнозируемый уровень, когда х = 0. Если х = 0 находится достаточно далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам.Пример:Представим простой способ интерпретации коэффициентов линейного уравнения регрессии у = a + bх, постоянная а дает прогнозируемое значение у (в единицах), если х = 0.

Как можно использовать полученные значимые оценки коэффициентов в эк. анализе?

Можно предположить, что данный коэффициент показывает предельное изменение зависимого параметра при изменении объясняющей переменной. Или для прогнозирования, для выявления знака зависимости одной переменной от другой, для расчета эластичности.

Как модель регрессии по времени может быть использована для предсказания

Значений зависимой переменной?

В модель регрессии по времени включена переменная времени и подставив нужное значение (номер периода, для которого выполняется прогноз) мы получаем прогнозное значение зависимой переменной для данного периода.

Каковы условия и ограничения для использования модели регрессии по времени для прогнозирования?

Должны выполняться условия Гаусса-Маркова.

I.Регрессионная модель линейна по параметрам (коэффициентам), корректно специфицирована, и содержит аддитивный случайный член.

II.Случайный член имеет нулевое среднее.

III. Объясняющая переменная не коррелирована со случайным членом.

IV.Наблюдаемые значения случайного члена не коррелированы друг с другом.

V.Случайный член имеет постоянную дисперсию

VI.Случайный член распределен нормально (необязательное, но часто используемое условие).

· Наблюдение должно включать Т+m наблюдений, из которых T – используется для построения регрессии (желательно высокое Т для точности), а последние m применяются для анализа точности предсказания. После проведения проверки можно построить прогноз на ближайшие несколько периодов, в среднем не далее 5% от длины промежутка выборки – чаще еще меньше.

Как можно использовать модель регрессии по факторной независимой переменной для прогнозирования?

С помощью регрессии по факторной независимой переменной можно прогнозировать поведение зависимой переменной в зависимости от изменения объясняющей переменной. Если в уравнение регрессии (с оцененными параметрами) подставить какое-то значение объясняющей переменной, то мы получим прогноз реакции зависимой переменной на изменение значения объясняющей переменной.

Какие проблемы и трудности возникают при использовании модели регрессии по

Факторной независимой переменной для прогнозирования?

Эконометрические модели строятся из-за 2 причин. Во-первых, это прогнозирование; при высоком показателе R 2 модель может дать очень хороший прогноз зависимой переменной на будущее. Во-вторых, для объяснения определенных зависимостей; в такой ситуации R 2 может быть низким, но зато знак коэффициента при независимой переменной будет определен однозначно, что даст исследователю информацию о виде связи между показателями. Если модель строилась по первой причине и не имеет высокого R-квадрата, использовать ее для прогнозирования бесполезно, так как результат будет далеким от совершенства.

Предпосылки регрессионного анализа. Условия Гаусса-Маркова

В чем состоят условия Гаусса-Маркова?

1. Модель линейна по параметрам (коэффициентам), правильно специфицирована, содержит аддитивный случайный член.

2. Объясняющая переменная не коррелированна со случайным членом

3. Математическое ожидание случайного члена равно нулю (E(u_i)=0 для всех i)

4. Случайный член гомоскедастичен (то есть его значение в каждом наблюдении получено из распределения с постоянной теоретической дисперсией: σ 2 _ui =σ 2 _u для всех i)

5. Значения случайного члена имеют взаимно независимые распределения (u_i распределен независимо от u_j для всех j≠i).

6. Случайный член имеет нормальное распределение (необязательное, но часто используемое условие).

Какой вывод относительно оцениваемого уравнения регрессии можно сделать из

Выполнимости условий Гаусса-Маркова?

МНК-оценка в данном случае является лучшей оценкой в классе линейных.

Видео:Уравнение линейной регрессии. Интерпретация стандартной табличкиСкачать

Интерпретация уравнения регрессии

Видео:Нелинейная регрессия в MS Excel. Как подобрать уравнение регрессии? Некорректное значение R^2Скачать

Интерпретация уравнения регрессии

Интерпретация регрессионных уравнений Существует два этапа интерпретации уравнения регрессии. Первый этап Уточнить, потому что уравнения интерпретируются устно Тот, кто не является статистиком. Во вторых это Нет необходимости решать, делать это или больше. Тщательное исследование зависимости. Оба этапа очень важны.

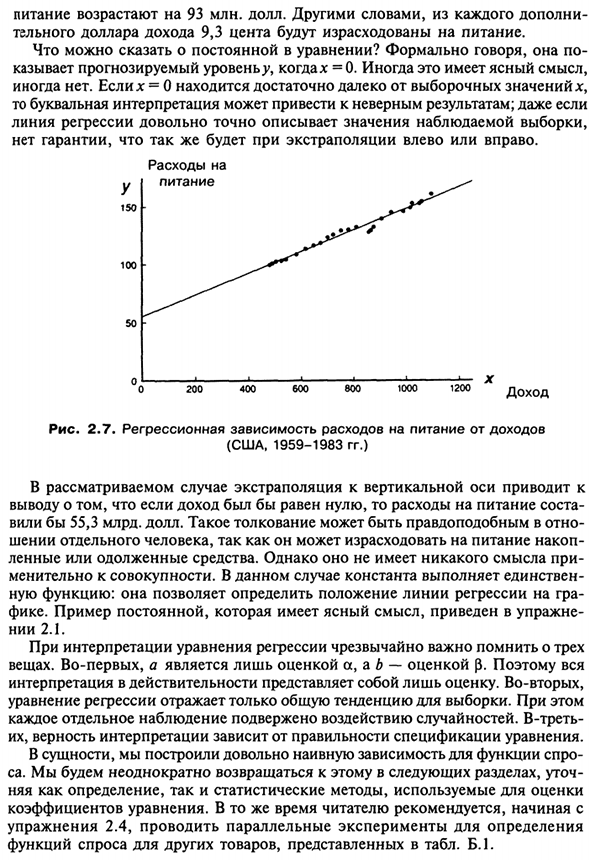
На втором этапе мы рассмотрим несколько поз А пока давайте обратим основное внимание на первый этап. Это объясняет Определяется регрессионной моделью функции спроса, то есть регрессией между расами Потребители переходят на еду (у) и располагаемый личный доход (х) Данные Отображается в графическом формате (рисунок 2.7). Предположим, что истинная модель описывается y = a + $ x + u, (2,41) И регрессионная оценка £ = 55,3 + 0,093 *. (2,42)

Данные приведены в таблице. Б.1 в США за период с 1959 по 1983 год. Людмила Фирмаль

Полученные результаты можно интерпретировать следующим образом: коэффициент в х (коэффициент градиента) Единица у увеличивается на 0,093 единицы. х и у оба измеряются в мил Миллиарды долларов по фиксированной цене. Поэтому склон Если выручка увеличится на 1 миллиард долларов, 64 Питательные вещества увеличились на 93 миллиона долларов.

Это значит Из реальных долларовых доходов 9,3 цента тратятся на еду. Как насчет констант уравнения? Формально она Если x = 0, указывает уровень прогнозирования ^. Это ясно имеет смысл. Иногда нет. Если х = 0 достаточно далеко от значения выборки х, В этом случае буквальная интерпретация может привести к неверным результатам.

Даже если Линия регрессии является очень точным представлением наблюдаемого значения выборки. Нет гарантии, что то же самое произойдет с экстраполяцией влево или вправо. в 150 грамм 100 грамм 50 Стоимость пища 200 400 600 800 —100 • ”0 120—0 X доходов Рисунок 2.7. Зависимость расходов на питание от дохода (США, 1959-1983).

В рассматриваемом случае путем экстраполяции на вертикальную ось Если доход равен нулю, стоимость еды Сделал бы 55,3 миллиарда долларов. Такое толкование может быть правдоподобным в отношении Лица, которые могут тратить накопления пищи Кредиты или заемные средства. Тем не менее, это не имеет смысла, если По отношению ко всему.

В этом случае константа сделает единственное Функция: может определить положение линии регрессии на графике Поддельный. Примеры констант с ясным значением приведены в упражнении. Институт 2.1. При интерпретации уравнений регрессии очень важно помнить три Вещь. Во-первых, a является только оценкой a, а a b является оценкой (3. Интерпретация на самом деле просто оценка.

Во-вторых Уравнение регрессии отражает только общую тенденцию выборки. В то же время Индивидуальные наблюдения подвержены случайности. третий В этих случаях точность интерпретации зависит от точности спецификации уравнения. По сути, мы построили довольно простую зависимость от функции спроса Мы вернемся к этому в следующем разделе и уточнить.

Определяя как определения, так и статистические методы, используемые при измерении Коэффициент уравнения. В то же время читателям рекомендуется начать с Упражнение 2.4, определить путем проведения параллельных экспериментов Функция спроса на другие товары приведена в таблице. B.1. После оценки регрессии возникают следующие вопросы:

Есть ли способ определить точность оценки? Это очень важно Рост будет обсуждаться в следующем разделе. Сначала рассмотрим дальше Подробно объясните роль остаточного члена и его влияние на оценки a и p. Интерпретация уравнений линейной регрессии.

Представьте себе простой способ интерпретации линейных коэффициентов. Людмила Фирмаль

Уравнение регрессии у = а + бх Если есть простая естественная единичная переменная Измерение. Сначала увеличим х на 1 единицу ( Единица переменной х) увеличивается у в б (единица переменной у). Второй этап Проверка того, что собой представляет хна на самом деле, Замените слово «единица измерения» на фактическое количество.

Третий этап Проверка возможности более простого выражения результата Это может быть не очень удобно. В примере В этом разделе указана единица измерения для х и у Потому что миллиарды долларов были потрачены, Замечательное упрощение. Константа а дает предсказанное значение у (единица ^). х = 0 Это может иметь или не иметь смысла в зависимости от значения Конкретная ситуация. Упражнение 1 2.1.

Регрессия стоимости продуктов питания (на основе того же Данные, для которых уже описана функция спроса, описанная в тексте) Меню определено как f = 1 в 1959 году, t = 2 в 1960 году и т. Д. Нини: у = 95,3 + 2,53 /. Интерпретация в Сравнение результатов оценки регрессии с аналогом Аналогичные результаты для модели регрессии функции спроса Пожалуйста, смотрите текст.

В этом случае постоянная Есть простая интерпретация. 2.2. Регрессивная зависимость от одноразовой зависимости стоимости жилья 1 Упражнение 2.4 особенно важно в том смысле, что оно запускает серию регрессий для развлечения. Общий спрос. Это оценивается читателем на протяжении всей книги.

Если это упражнение Если это делается группой студентов, учитель должен дать студентам задания Товарные. Более подробная информация о доступных данных доступна в Приложении B.go Личный доход в соответствии с таблицей. B.1, оба количества Можно оформить миллиарды долларов с 1959 по 1983 В следующем формате: j> = -27,6 + 0,178х.

Регрессивная зависимость и определение стоимости жилья с течением времени То же самое, что и упражнение 2.1, можно выразить как: f = 48,9 + 4,84 г. Вот экономическая интерпретация этих регрессий. У них разные предложения Описание тех же данных в переменной y. Сколько они Вы можете согласиться? 2,3.

Создайте уравнение регрессии между p и e из данных упражнения 1.3, сначала используйте все 12 наблюдений, затем исключите наблюдения 1. Дает экономическую интерпретацию для Японии. 2,4. В таблице. B.1 — потребительские расходы США располагаемый личный доход за период 1959-1983 гг. Назовите один продукт — не еду, а не домашнюю Пропустите регрессию между y и x. х — располагаемый личный доход, использующий Данные за 25 лет.

Интерпретация коэффициентов регрессии 2.5. Таким образом, регрессия между характеристиками продукта и временем Мы сделаем это в упражнении 2.1. Правильная интерпретация и сравнение У нее есть интерпретация регрессии, полученная в упражнении 2.4. 2.6. Два человека строят один и тот же набор временных тенденций 25 наблюдений за переменной y с использованием модели: у = а + р / + и

Где t — время (принимает значения непрерывно от 1 до 25), а -case Член чаепития. Получите первое уравнение: j> = 6,70 + 1,79 /. Вторая по ошибке оценивает регрессию между / и у и этим уравнением По мнению: t = -0,25 + 0,44 >>. Из этого уравнения он получает: у = 0,57 + 2,27 /. Объясните это уравнение и несоответствие между уравнениями, Получено первым исследователем. 2,7.

Как изменяется регрессионный балл в упражнении 2.1 Фактическая дата (1959-1983) используется как / вместо числа из 1 до 25? 2,8. Исследователи, 1 Не начинайте сначала вычислять коэффициент регрессии. Заполнены большинство арифметических расчетов в упражнении 1.3. 2 Учителя являются учениками, если это групповое занятие.

Удар, чтобы дать задачу оценки регрессии различных видов товаров в дополнение к еде жилья.люги, основанные на данных АМЕ (у) и общем располагаемом личном доходе (х) Риканская экономика (обе измеряются в миллиардах долларов) Фиксированная цена) с использованием данных и модели временных рядов за год: y = a + px + u. 1.

Исследователь выполняет регрессионный анализ, чтобы получить уравнение. Используйте обычный метод наименьших квадратов. Если предположить, что Обе ценности могут быть значительно недооценены внутренней системой Личные счета за желание людей не платить налоги Правительство, исследователи принимают два альтернативных улучшения Недооцененная оценка. 2.

Исследователи добавляют $ 90 млрд к показателю каждый год >> и Показатель х 200 миллиардов долларов. 3. Исследователь увеличивает x и y на 10% Каждый год. Оценить влияние корректировок (2) и (3) на результаты рег. ressii. 2.9. Исследователи имеют общие годовые данные временных рядов.

Заработная плата (W), валовой доход (P) и валовой доход (Y) Для страны сроком на n лет. По определению Y = W + T1. Получите регулярное уравнение, используя метод наименьших квадратов Рссии: fr = a0 + aiY; ft = Z> 0 + bxY. Указывает, что коэффициент регрессии автоматически удовлетворяет Следующее уравнение: но х + * я = 1; * o + K = 0. Интуитивно объясните, почему так должно быть. 2.10.

Исследователи не имеют нестохастической части истинной модели у пропорционально х. y = $ x + u. Исходя из исходного принципа, выведите формулу b, оценка МНК б. В этом случае (2.31) указывает, что это можно записать следующим образом. S = bj] + b2J, xj -2 £ Xx,. > 7 Для этого b = 2, xiyi / Zxf. 2,11. Выведите оценку наименьших квадратов модели из первого предположения. у = а + у. 68 То есть у это просто сумма констант Случайные участники с нами. Сначала переопределите 5, а затем дифференцируйте Цитирование.