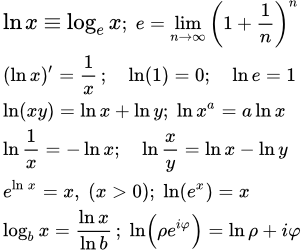Что означает in в уравнении (3 видео)

Натуральный логарифм, функция ln x

Содержание

Определение
График натурального логарифма ln x
Свойства натурального логарифма
Область определения, множество значений, экстремумы, возрастание, убывание
Значения ln x
Основные формулы натуральных логарифмов
Основное свойство логарифмов и его следствия
Формула замены основания
Обратная функция
Производная ln x
Интеграл
Выражения через комплексные числа
Разложение в степенной ряд
Логарифм. Натуральный логарифм.
Натуральные логарифмы. Функция y=ln x, ее свойства, график, дифференцирование
💥 Видео

Видео:РЕШЕНИЕ УРАВНЕНИЙ |ПОДРОБНОЕ ОБЪЯСНЕНИЕ КАК РЕШИТЬ УРАВНЕНИЯ / ПРОСТЫЕ УРАВНЕНИЯ 2 КЛАСС МАТЕМАТИКАСкачать

Определение

Натуральный логарифм широко используется в математике, поскольку его производная имеет наиболее простой вид: (ln x )′ = 1/ x .

Исходя из определения, основанием натурального логарифма является число е:
е ≅ 2,718281828459045. ;
.

Видео:Простые уравнения. Как решать простые уравнения?Скачать

График натурального логарифма ln x

График натурального логарифма (функции y = ln x ) получается из графика экспоненты зеркальным отражением относительно прямой y = x .

Натуральный логарифм определен при положительных значениях переменной x . Он монотонно возрастает на своей области определения.

При x → 0 пределом натурального логарифма является минус бесконечность ( – ∞ ).

При x → + ∞ пределом натурального логарифма является плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a растет быстрее логарифма.

Видео:Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Свойства натурального логарифма

Область определения, множество значений, экстремумы, возрастание, убывание

Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумов не имеет. Основные свойства натурального логарифма представлены в таблице.

Область определения	0
Область значений	– ∞
Монотонность	монотонно возрастает
Нули, y = 0	x = 1
Точки пересечения с осью ординат, x = 0	нет
+ ∞
– ∞

Значения ln x

Видео:Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Основные формулы натуральных логарифмов

Формулы, вытекающие из определения обратной функции:

Основное свойство логарифмов и его следствия

Формула замены основания

Любой логарифм можно выразить через натуральные логарифмы с помощью формулы замены основания:

Доказательства этих формул представлены в разделе «Логарифм».

Видео:Что такое уравнениеСкачать

Обратная функция

Обратной для натурального логарифма является экспонента.

Если 0)» style=»width:132px;height:20px;vertical-align:-11px;background-position:-296px -320px»> , то

Видео:Урок 6 УРАВНЕНИЕ И ЕГО КОРНИ 7 КЛАСССкачать

Производная ln x

Производная натурального логарифма:
.
Производная натурального логарифма от модуля x :
.
Производная n-го порядка:
.
Вывод формул > > >

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Интеграл

Видео:Сложные уравнения. Как решить сложное уравнение?Скачать

Выражения через комплексные числа

Рассмотрим функцию комплексной переменной z :
.
Выразим комплексную переменную z через модуль r и аргумент φ:
.
Используя свойства логарифма, имеем:
.
Или
.
Аргумент φ определен не однозначно. Если положить
, где n – целое,
то будет одним и тем же числом при различных n .

Поэтому натуральный логарифм, как функция от комплексного переменного, является не однозначной функцией.

Видео:Ларинский вариант ЕГЭ №449. Математика на 100 балловСкачать

Разложение в степенной ряд

При имеет место разложение:

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов . Опубликовано: 05-04-2014 Изменено: 20-03-2017

Видео:КАК РЕШАТЬ ПРОПОРЦИИ?Скачать

Логарифм. Натуральный логарифм.

За основание логарифмов нередко берут цифру е = 2,718281828. Логарифмы по данному основанию именуют натуральным. При проведении вычислений с натуральными логарифмами общепринято оперировать знаком ln, а не log; при этом число 2,718281828, определяющие основание, не указывают.

Другими словами формулировка будет иметь вид: натуральный логарифм числа х — это показатель степени, в которую нужно возвести число e, чтобы получить x.

Так, ln(7,389. )= 2, так как e 2 =7,389. . Натуральный логарифм самого числа e= 1, потому что e 1 =e, а натуральный логарифм единицы равен нулю, так как e 0 = 1.

Само число е определяет предел монотонной ограниченной последовательности

вычислено, что е = 2,7182818284. .

Весьма часто для фиксации в памяти какого либо числа, цифры необходимого числа ассоциируют с какой-нибудь выдающейся датой. Скорость запоминания первых девяти знаков числа е после запятой возрастет, если заметить, что 1828 — это год рождения Льва Толстого!

Число е является иррациональным. Французский математик Эрмит (1822 — 1901) обосновал, что это число не может быть корнем никакого алгебраического уравнения с целыми коэффициентами. Такие иррациональные числа именуются трансцендентными.

На сегодняшний день существуют достаточно полные таблицы натуральных логарифмов.

График натурального логарифма (функции y = ln x) является следствием графика экспоненты зеркальным отражением относительно прямой у = х и имеет вид:

Натуральный логарифм может быть найден для каждого положительного вещественного числа a как площадь под кривой y = 1/x от 1 до a.

Элементарность этой формулировку, которая состыковывается со многими другими формулами, в которых задействован натуральный логарифм, явилось причиной образования названия «натуральный».

Если анализировать натуральный логарифм, как вещественную функцию действительной переменной, то она выступает обратной функцией к экспоненциальной функции, что сводится к тождествам:

По аналогии со всеми логарифмами, натуральный логарифм преобразует умножение в сложение, деление в вычитание:

Логарифм может быть найден для каждого положительного основания, которое не равно единице, а не только для e, но логарифмы для других оснований отличаются от натурального логарифма только постоянным множителем, и, обычно, определяются в терминах натурального логарифма.

Проанализировав график натурального логарифма, получаем, что он существует при положительных значениях переменной x. Он монотонно возрастает на своей области определения.

При x →0 пределом натурального логарифма выступает минус бесконечность ( –∞ ).При x → +∞ пределом натурального логарифма выступает плюс бесконечность ( + ∞ ). При больших x логарифм возрастает довольно медленно. Любая степенная функция x a с положительным показателем степени a возрастает быстрее логарифма. Натуральный логарифм является монотонно возрастающей функцией, поэтому экстремумы у него отсутствуют.

Использование натуральных логарифмов весьма рационально при прохождении высшей математики. Так, использование логарифма удобно для нахождения ответа уравнений, в которых неизвестные фигурируют в качестве показателя степени. Применение в расчетах натуральных логарифмом дает возможность изрядно облегчить большое количество математических формул. Логарифмы по основанию е присутствуют при решении значительного числа физических задач и естественным образом входят в математическое описание отдельных химических, биологических и прочих процессов. Так, логарифмы употребляются для расчета постоянной распада для известного периода полураспада, или для вычисления времени распада в решении проблем радиоактивности. Они выступают в главной роли во многих разделах математики и практических наук, к ним прибегают в сфере финансов для решения большого числа задач, в том числе и в расчете сложных процентов.

Видео:1. Что такое дифференциальное уравнение?Скачать

Натуральные логарифмы. Функция y=ln x, ее свойства, график, дифференцирование

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом занятии мы изучим следующую тему: «Натуральные логарифмы. Функция y=ln x, её свойства, график, дифференцирование». Для начала дадим определение новому для нас понятию «натуральный логарифм», в основании которого стоит число е. После этого рассмотрим основные свойства функции y=ln x, построим график натурального логарифма, поговорим о его дифференцировании.