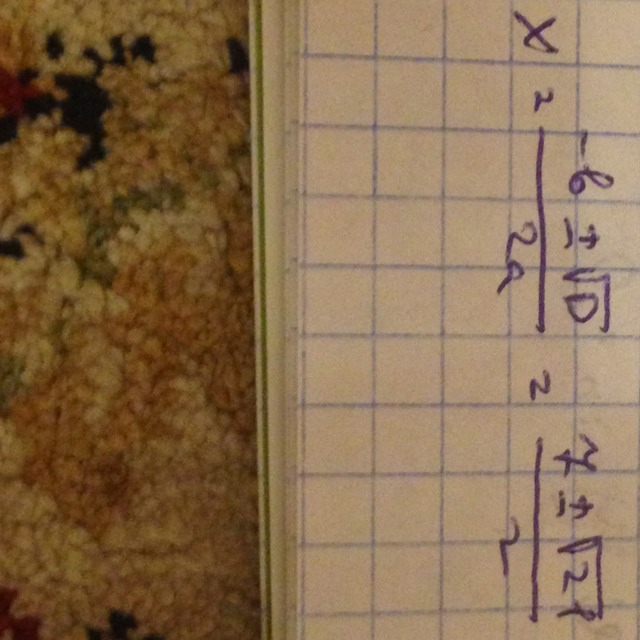Что делать если в квадратном уравнении не извлекается корень

Видео:Как разобраться в корнях ? Квадратный корень 8 класс | Математика TutorOnlineСкачать

Извлечение корней: методы, способы, решения

Из этой статьи вы узнаете:

• что такое «извлечение корня»;
• в каких случаях он извлекается;
• принципы нахождения значения корня;
• основные способы извлечения корня из натуральных и дробных чисел.

Видео:Что делать если корни не извлекаются? #shortsСкачать

Что такое «извлечение корня»

Для начала введем определение «извлечение корня».

Извлечение корня — процесс нахождения значения корня.

При извлечении корня n -ной степени из числа a, мы находим число b , n -ная степень которого равняется a . Если мы нашли такое число b , можно утверждать, что корень извлечен.

Выражения «извлечение корня» и «нахождение значения корня» равнозначны.

Видео:Что делать если корни не извлекаются? #егэ2024 #егэматематика #огэ #огэ2024 #огэматематикаСкачать

В каких случаях извлекается корень?

Корень n -ной степени можно извлечь из числа a точно в случае, если a можно представить в виде n -ной степени некоторого числа b .

4 = 2 × 2 , следовательно, из числа 4 можно точно извлечь квадратный корень, который равен 2

Когда корень n -ной степени из числа a невозможно представить в виде n -ной степени числа b , то такой корень не извлекается, либо извлекается только приближенное значение корня с точностью до любого десятичного разряда.

Видео:Как извлекать квадратный корень без калькулятора, даже если он не извлекается нацелоСкачать

Принципы нахождения значения корня и способы их извлечения

• Использование таблицы квадратов, таблицы кубов и т.д.
• Разложение подкоренного выражения (числа) на простые множители
• Извлечение корней из дробных чисел
• Извлечение корня из отрицательного числа
• Поразрядное нахождение значения корня

Необходимо понять, по каким принципам находится значение корней, и каким образом они извлекаются.

Главный принцип нахождения значения корней — основываться на свойствах корней, в том числе на равенстве: b n n = b , которое является справедливым для любого неотрицательного числа b .

Начать следует с наиболее простого и очевидного способа: таблицы квадратов, кубов и т.д.

Когда таблицы под руками нет, вам поможет способ разложения подкоренного числа на простые множители (способ незатейливый).

Стоит уделить внимание извлечению корня из отрицательного числа, что является возможным для корней с нечетными показателями.

Изучим, как извлекать корни из дробных чисел, в том числе из смешанных чисел, обыкновенных и десятичных дробей.

И потихоньку рассмотрим способ поразрядного нахождения значения корня — наиболее сложного и многоступенчатого.

Использование таблицы квадратов, кубов и т.д.

Таблица квадратов включает в себя все числа от 0 до 99 и состоит из 2 зон: в первой зоне можно составить любое число до 99 с помощью вертикального столбца с десятками и горизонтальной строки с единицами, во второй зоне содержатся все квадраты образуемых чисел.

Таблица квадратов

Существуют также таблицы кубов, четвертой степени и т.д., которые созданы по принципу, аналогичному таблице квадратов.

Таблица кубов

Принцип функционирования таких таблиц прост, однако их часто нет под рукой, что значительно усложняет процесс извлечение корня, поэтому необходимо владеть минимум несколькими способами извлечения корней.

Видео:Как вычислить любой неизвлекаемый кореньСкачать

Разложение подкоренного числа на простые множители

Наиболее удобный способ нахождения значения корня после таблицы квадратов и кубов.

Способ разложения подкоренного числа на простые множители подразумевает под собой представление числа в виде степени с необходимым показателем, что дает нам возможность получить значение корня.

Извлечем квадратный корень из 144 .

Разложим 144 на простые множители:

Таким образом: 144 = 2 × 2 × 2 × 2 × 3 × 3 = ( 2 × 2 ) 2 × 3 2 = ( 2 × 2 × 3 ) 2 = 12 2 . Следовательно, 144 = 12 2 = 12 .

Также при использовании свойств степени и корней можно записать преобразование немного по-другому:

144 = 2 × 2 × 2 × 2 × 3 × 3 = 2 4 × 3 2 = 2 4 × 3 2 = 2 2 × 3 = 12

144 = 12 — окончательный ответ.

Видео:Квадратный корень. 8 класс.Скачать

Извлечение корней из дробных чисел

Запоминаем: любое дробное число должно быть записано в виде обыкновенной дроби.

Следуя свойству корня из частного, справедливым является следующее равенство:

p q n = p n q n . Исходя из этого равенства, необходимо воспользоваться правилом извлечения корня из дроби: корень из дроби равен от деления корня числителя на корень знаменателя.

Рассмотрим пример извлечения корня из десятичной дроби, поскольку извлечь корень из обыкновенной дроби можно с помощью таблицы.

Необходимо извлечь кубический корень из 474 , 552 . Первым делом, представим десятичную дробь в виде обыкновенной: 474 , 552 = 474552 / 1000 . Из этого следует: 474552 1000 3 = 474552 3 1000 3 . Затем можно приступить к процессу извлечения кубических корней в числителе и знаменателе:

474552 = 2 × 2 × 2 × 3 × 3 × 3 × 13 × 13 × 13 = ( 2 × 3 × 13 ) 3 = 78 3 и 1000 = 10 3 , то

474552 3 = 78 3 3 = 78 и 1000 3 = 10 3 3 = 10 .

Завершаем вычисления: 474552 3 1000 3 = 78 10 = 7 , 8 .

Видео:Решение квадратных уравнений. Дискриминант. 8 класс.Скачать

Извлечение корня из отрицательных чисел

Если знаменатель является нечетным числом, то число под знаком корня может оказаться отрицательным. Из этого следует: для отрицательного числа — a и нечетного показателя корня 2 n — 1 справедливо равенство:

— a 2 × n — 1 = — a 2 × n — 1

Правило извлечения нечетной степени из отрицательных чисел: чтобы извлечь корень из отрицательного числа необходимо извлечь корень из противоположного ему положительного числа и поставить перед ним знак минус.

— 12 209 243 5 . Для начала необходимо преобразовать выражение, чтобы под знаком корня оказалось положительно число:

— 12 209 243 5 = 12 209 243 — 5 ​​​​​​

Затем следует заменить смешанное число обыкновенной дробью:

12 209 243 — 5 = 3125 243 — 5

Пользуясь правилом извлечения корней из обыкновенной дроби, извлекаем:

3125 243 — 5 = — 3125 5 243 5

Вычисляем корни в числителе и знаменателе:

— 3125 5 243 5 = — 5 5 5 3 5 5 = — 5 3 = — 1 2 3

Краткая запись решения:

— 12 209 243 5 = 12 209 243 — 5 = 3125 243 — 5 = — 3125 5 243 5 = — 5 5 5 3 5 5 = — 5 3 = — 1 2 3 .

Ответ: — 12 209 243 5 = — 1 2 3 .

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Поразрядное нахождение значения корня

Бывают случаи, когда под корнем находится число, которое не получается представить в виде n — ной степени некоторого числа. Но необходимо знать значение корня с точностью до некоторого знака.

В таком случае необходимо воспользоваться алгоритмом поразрядного нахождения значения корня, с помощью которого можно получить достаточное количество значений искомого числа.

Как это происходит, разберем на примере извлечения квадратного корня из 5 .

Сперва необходимо найти значение разряда единиц. Для этого начнем перебирать значения 0 , 1 , 2 , . . . , 9 , вычисляя при этом 0 2 , 1 2 , . . . , 9 2 до необходимого значения, которое больше, чем подкоренное число 5 . Все это удобно представить в виде таблицы:

Значение ряда единиц равняется 2 ( т а к к а к 2 2 5 , а 2 3 > 5 ) . Переходим в разряду десятых — будем возводить в квадрат числа 2 , 0 , 2 , 1 , 2 , 2 , . . . , 2 , 9 , , сравнивая полученные значения с числом 5 .

Поскольку 2 , 2 2 5 , а 2 , 3 2 > 5 , то значение десятых равняется 2 . Переходим к нахождению значения сотых:

Таким образом, найдено значение корня из пяти — 2 , 23 . Можно находить значения корня дальше:

2 , 236 , 2 , 2360 , 2 , 23606 , 2 , 236067 , . . .

Итак, мы изучили несколько наиболее распространенных способов нахождения значения корня, воспользоваться которыми можно в любой ситуации.

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Некоторые приемы извлечения квадратного корня из числа

Разделы: Математика

Многим старшеклассникам часто приходится сталкиваться с заданиями типа “Сравните числа. ” или “Решите уравнение. ”, в которых или извлекаемый, но из неимоверно большого числа (настолько большого, что не поможет даже таблица квадратов) корень, либо неизвлекаемый. Конечно, можно воспользоваться калькулятором и не мучиться. Но как же быть с предстоящими экзаменами? Да и на контрольной работе особо техникой не воспользуешься.

Именно этот вопрос может стать прекрасной темой для исследовательской работы.

Исследуем некоторые способы извлечения квадратных корней из различных чисел.

Задачи:

• Познакомиться с историей квадратного корня
• Научиться извлекать квадратные корни без помощи электронно-вычислительной техники
• Познакомить с этими способами учащихся.

Данная тема очень актуальна, так как каждому выпускнику предстоит сдавать экзамены, а приобретённые навыки помогут не только на ЕГЭ по математике, но и на других предметах.

История квадратного корня.

Как мы знаем из определения, квадратный корень из числа а — это такое число, квадрат которого равен а, то есть решения уравнения относительно переменной х:

Квадратным корнем называют также функцию вещественной переменной х, которая каждому ставит в соответствие арифметическое значение корня.

Знак корня происходит из строчной латинской буквы (от латинского radix — корень), сросшейся с надстрочной чертой. Ранее надчеркивание выражения использовалось вместо заключения его в скобки. Так что есть всего лишь видоизменённый способ записи выражения .

Впервые такое обозначение использовал немецкий математик Томас Рудольф в 1525 году.

В ходе работы над данным исследованием можно обнаружить занимательную информацию. Оказывается, существует неофициальный праздник, посвящённый квадратному корню.

День квадратного корня — праздник, отмечаемый девять раз в столетие: в день, когда и число, и порядковый номер месяца являются квадратными корнями из двух последних цифр года (например, 2 февраля 2004 года: 02.02.04 или 3 марта 2009 года: 03.03.09). Ближайший такой праздник состоится 4 апреля 2016 года (04.04.16).

Впервые этот праздник отмечался 9 сентября 1981 года (09.09.81). Основателем праздника является школьный учитель Рон Гордон из города Редвуд Сити, штат Калифорния, США. Его дочь с помощью всемирных социальных сетей собрала группы поклонников этого праздника, где каждый может поделиться своим способом отметить эту необычную дату.

Главным блюдом на этом “праздничном столе” обычно являются варёные кубики из овощей и выпечка в форме математического знака квадратного корня.

По объективным математическим причинам это праздник отмечается строго девять раз в столетие (семь раз в первой половине века и дважды — во второй), всегда в одни и те же дни:

1. января ХХ01 года
2. февраля ХХ04 года
3. марта ХХ09 года
4. апреля XX16 года
5. мая ХХ25 года
6. июня ХХ36 года
7. июня ХХ49 года
8. августа ХХ64 года
9. сентября ХХ81 года.

При этом интересно заметить, что промежуток (в годах) между праздниками составляет непрерывную последовательность нечётных чисел: 3, 5, 7,9, 11, 13, 15, 17, 19.

Методы извлечения квадратного корня.

Рассмотрим несколько методов извлечения квадратного корня. Начнём с алгоритма для извлечения квадратного корня из целого и дробного числа; арифметического способа; метода грубой прикидки. Далее рассмотрим два замечательных (и весьма удобных) метода Герона.

Алгоритм для извлечения квадратного корня из целого числа нацело. Данный алгоритм требует вычислений в столбик. Изучим предложенный алгоритм, а затем применим для нескольких чисел.

Разбить число на группы по две цифры справа налево.

Для первой группы (она может в итоге состоять из двухзначного и однозначного числа) подобрать такую цифру, чтобы её квадрат был наибольшим и не превосходящим данное число.

Из первой группы вычитается квадрат найденного числа, а само число будет первым в ответе.

Далее работаем столбиком, то есть к остатку (если он есть) сносим следующую группу.

Самый сложный. Помните то число, которое было первым в ответе? Его необходимо умножить на 2, а затем справа к нему приписать ещё одну цифру, такую, чтобы произведение полученного числа на приписанную цифру было наибольшим, но не превосходило снесённое число. Эта самая цифра будет следующей в ответе.

Затем мы вычитаем столбиком полученное число и сносим следующую группу, если такая есть. И повторяем шаги 4-5, только берём уже все число, которое выходит в ответе.

Без примера разобраться с этим алгоритмом трудно. Начнём с числа попроще, с табличного значения.

Пример: вычислим .

Разбиваем число: 31’36

Для первой группы (31) подбираем цифру, чтобы её квадрат был максимален, но не превосходил группу. В данном случае это число 5, которое первым пойдёт в ответ.

, Пусть цифра – 6;

Пример: возьмём число повнушительнее, например

Разбиваем число:

Для первой группы (29) подбираем цифру, чтобы её квадрат был максимален, но не превосходил группу. В данном случае это число 5, которое первым пойдёт в ответ.

а) , Пусть цифра – 4;

б) , Пусть цифра – 7;

Если корень не извлекается из числа нацело, то нужно пользоваться тем же самым алгоритмом, добавив справа от исходного числа дробные группы ’00’ (чем больше групп, тем точнее результат). Если необходимо вычислить корень квадратный из дробного числа, то также пользуются данным алгоритмом, только дробную часть разбивать на группы необходимо слева направо, считая от запятой.

Для относительно небольших чисел существует арифметический способ вычисления их квадратного корня. Ну, мало ли на экзамене переволнуешься, и забудешь корень квадратный из 4. Бывает и не такое.

В чем суть метода. Для квадратов чисел справедливы следующие равенства:

То есть найдём, например: .

=5

В принципе, этим способом можно найти целую часть квадратного корня для чисел, из которых корень нацело не выносится.

=2 (и остаток 4)

Метод грубой прикидки может быть использован при наличии под рукой таблицы квадратов.

Например, вам необходимо грубо оценить значение .

Тогда можно поступить следующим образом. Нужно умножить исходное число на 100 (т.е. ) и найти ближайшие к полученному числу значения по таблице. В данном случае, это числа 484 и 529. Квадратными корнями для этих чисел являются 22 и 23. , , тогда

Аналогично, для больших чисел: найдём .

Древнегреческий учёный Герон, живший ещё в I веке нашей эры, придумал метод вычисления квадратных корней, который, возможно, используется в ваших собственных калькуляторах. Суть первого метода проще всего понять сразу на примере.

Найдём. Число не имеет рационального корня, поэтому возьмём корень с очень малой погрешностью. Это 1369, имеющее корень 37.

Разделим 1360 на 37. Получается .

Теперь сложим 37 и , получается .

Разделим результат на 2, получим . Безусловно, мы получаем число с погрешностью, но эту погрешность можно уменьшить, если повторить все операции ещё раз.

Второй метод Герона ещё проще, чем первый.

В этом случае, исходное число представляется как . где а 2 – ближайший точный квадрат, и считают по формуле

Например,

По моему мнению, методы Герона являются самыми простыми для понимания школьников, а также очень эффективными, так как имеют самую маленькую погрешность. Успехов на экзамене!

Видео:ЛОВИ ПРОДОЛЖЕНИЕ 😉 ДИСКРИМИНАТ ЧАСТЬ II #shorts #математика #егэ #огэ #профильныйегэСкачать

Что делать когда дискриминант не извлекается из под корня?

Алгебра | 5 — 9 классы

Что делать когда дискриминант не извлекается из под корня?

Пример такой : Х = 7 + / — (21 под корнем) / 2.

Если Дискриминант не извлекается из под корня.

То корни уравнения так и записываются.

Видео:#140. КАК ИЗВЛЕКАТЬ КОРНИ В СТОЛБИК? В ШКОЛЕ НЕ ПОКАЖУТ!Скачать

Формулы дискриминанта и корней?

Формулы дискриминанта и корней.

Видео:КОРЕНЬ БЕЗ КАЛЬКУЛЯТОРА 😉 #егэ #математика #профильныйегэ #shorts #огэСкачать

5x = 3x ^ 2 найти дискриминант и корни?

5x = 3x ^ 2 найти дискриминант и корни.

Видео:Математика| Разложение квадратного трехчлена на множители.Скачать

Найдите дискриминант и корни 6х² — 11х — 1 = 0?

Найдите дискриминант и корни 6х² — 11х — 1 = 0.

Видео:Как считать корни? #shortsСкачать

Найдите дискриминант и корни?

Найдите дискриминант и корни.

Видео:Квадратные уравнения #shorts Как решать квадратные уравненияСкачать

Найдите ошибку, дискриминант 573 получается, а корень не извлекается?

Найдите ошибку, дискриминант 573 получается, а корень не извлекается.

Как такие корни извлекать?

Видео:В интернете опять врут! Извлечение корня по методу, который на самом деле не работаетСкачать

При каких значениях дискриминанта D квадратное уравнение не имеет корней?

При каких значениях дискриминанта D квадратное уравнение не имеет корней.

Видео:Как вычислить корень без калькулятора.Скачать

Пожалуйста решите уравнение 3x ^ 2 — 2 — 5 = 0 никак не могу найти дискриминант ?

Пожалуйста решите уравнение 3x ^ 2 — 2 — 5 = 0 никак не могу найти дискриминант ?

Из — под корня не извлекается.

Видео:КАК ИЗВЛЕЧЬ КОРЕНЬ БЕЗ КАЛЬКУЛЯТОРАСкачать

Здравствуйте, помогите пожалуйста?

Здравствуйте, помогите пожалуйста.

Что делать если корень не извлекается из дискриминанта, пример числа 128.

Видео:Как решить квадратное уравнение за 30 секунд#математика #алгебра #уравнение #дискриминант #репетиторСкачать

Дайте определение тождества?

Дайте определение тождества.

Что называют дискриминантом квадратного уравнения?

Сколько корней может иметь квадратное уравнение?

Если вам необходимо получить ответ на вопрос Что делать когда дискриминант не извлекается из под корня?, относящийся к уровню подготовки учащихся 5 — 9 классов, вы открыли нужную страницу. В категории Алгебра вы также найдете ответы на похожие вопросы по интересующей теме, с помощью автоматического «умного» поиска. Если после ознакомления со всеми вариантами ответа у вас остались сомнения, или полученная информация не полностью освещает тематику, создайте свой вопрос с помощью кнопки, которая находится вверху страницы, или обсудите вопрос с посетителями этой страницы.

Task / 25774876 — — — — — — — — — — — — — — — — — — — — — Решите уравнениеSinx * cosx * sin3x — cos3x * sin²x = 6ctgx — — — — — — — — — — — — — — — — — — Sinx(cosx * sin3x — cos3x * sinx) = 6ctgx ; sinx * sin(3x — x) = 6ctqx ; sinx * sin2x = 6ctqx ; ..

Графики в прикрепе Ответ : — 1 ; 2.

Пусть цена тетради х руб. , цена ручки у руб. , ценакарандаша z руб. Тогда стоимость покупки Маши : 2х + 4у + z = 30 (руб. ) Стоимость покупки Саши : 4x + 5y + 2z = 51 (руб. ) Найти стоимость покупки Даши : 2х + 3у + z = ? (руб. ) Стоимость по..

(3 + а) * (3 — а) но никак не 1.

В 5 классе алгебра не бывает.

128 : 2 = 64 см² площадь одной грани сторона куба равна√64 = 8 см v = 8³ = 512 cм³.

Решение смотри на фотографии.

1. 5 — 4( — 2) = 5 — ( — 8) = — 13 2. 1 5. — 2.

📽️ Видео

Извлечение корня в столбик sqrt2Скачать