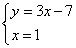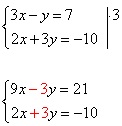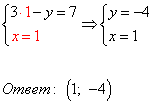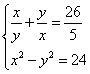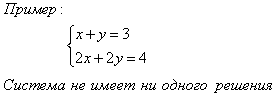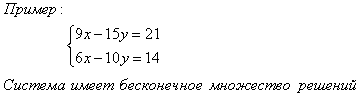Число решений системы равно числу общих точек графиков уравнений

Видео:Решение системы линейных уравнений графическим методом. 7 класс.Скачать

Математика

Видео:Алгебраическое определение количества решений системы линейных уравнений | Алгебра IСкачать

Тестирование онлайн

Видео:Графический способ решения систем уравнений. Алгебра, 9 классСкачать

Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.

При решении системы уравнений используют свойства, справедливые для решения уравнений.

Видео:Алгебра 9 класс. Графическое решение систем уравненийСкачать

Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

Видео:Математика это не ИсламСкачать

Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

Видео:Количество решений системы уравнений. УпражнениеСкачать

Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Метод введения новых переменных

Замена переменных может привести к решению более простой системы уравнений, чем исходная.

Рассмотрим решение системы

Введем замену 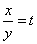, тогда

Переходим к первоначальным переменным

Видео:Задание 23 из ОГЭ Построение графиков функций с модулем | МатематикаСкачать

Особые случаи

Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система

1) Если 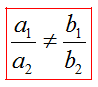, то система имеет единственное решение.

2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.

Видео:Решение системы уравнений графическим методомСкачать

Метод Гаусса*

Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.

Видео:Решение систем уравнений методом подстановкиСкачать

Графический метод решения системы линейных уравнений

Расположение графиков и количество решений системы линейных уравнений

Рассмотрим систему двух уравнений: $ <left< begin 3x-y = 5 \ 3x+2y = 8end right.>$

Построим график каждого из уравнений и найдём точку пересечения.

Точка пересечения (2;1)

Подставим координаты точки пересечения в уравнение:

$ <left< begin3 cdot 2-1 ≡ 5\ 3cdot2+2cdot1 ≡ 8end right.> Rightarrow$ (2;1) — решение системы

Таким образом, точка пересечения графиков уравнений является решением системы.

Графики двух уравнений системы могут пересекаться, быть параллельными и совпадать. Получаем разное количество решений системы в зависимости от соотношения коэффициентов уравнений:

Видео:Как решать систему уравнений графическим методом? | Математика | TutorOnlineСкачать

Число решений системы равно числу общих точек графиков уравнений

Другими словами, если задано несколько уравнений с одной, двумя или больше неизвестными, и все эти уравнения (равенства) должны одновременно выполняться , такую группу уравнений мы называем системой.

Объединяем уравнения в систему с помощью фигурной скобки:

Графический метод

Недаром ответ записывается так же, как координаты какой-нибудь точки.

Ведь если построить графики для каждого уравнения в одной системе координат, решениями системы уравнений будут точки пересечения графиков.

Например, построим графики уравнений из предыдущего примера.

Пример 1

Для этого сперва выразим y y y в каждом уравнении, чтобы получить функцию (ведь мы привыкли строить функции относительно x x x ):

Для того чтобы графически решить систему уравнений с двумя переменными нужно:

1) построить графики уравнений в одной системе координат;
2) найти координаты точек пересечения этих графиков (координаты точек пересечения графиков и есть решения системы);

Разберем это задание на примере.

Решить графически систему линейных уравнений.

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Пример 2

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может:

а) иметь единственное решение;

б) не иметь решений;

в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Пример 3

Графическое решение системы

Пример 4

Решить графическим способом систему уравнений.

Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.

Прямую y=2x-3 провели через точки (0; -3) и (2; 1).

Прямую y=x+1 провели через точки (0; 1) и (2; 3).

Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.

Пример 5

Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.

Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).

Наши прямые пересеклись в точке В(-2; 5).

ОБЯЗАТЕЛЬНО: Познакомимся с видео, где нам объяснят как решаются системы линейных уравнений графическим способом. РАССКАЖУТ, КАК РЕШАТЬ СИСТЕМЫ ГРАФИЧЕСКИ.

Видео YouTube

💡 Видео

#75 Урок 36. Определение количества решений системы уравнений. Алгебра 7 класс.Скачать

Система уравнений не имеет решений или имеет бесчисленное множество решенийСкачать

Как построить график функции без таблицыСкачать

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Графическое решение систем уравнений | Системы уравнений | Алгебра 1Скачать

Графический метод решения систем линейных уравнений 7 классСкачать

Как решают уравнения в России и СШАСкачать

Система уравнений и возможное число решенийСкачать