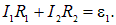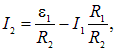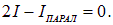Число независимых уравнений составляемых по законам кирхгофа (4 видео)

4.5. Правила Кирхгофа

На практике очень часто встречаются сложные (разветвленные) электрические цепи, для расчета которых удобно использовать правила Кирхгофа (рис. 4.22).

Рис. 4.22. Г. Кирхгоф (1824–1887) — немецкий физик

Первое правило Кирхгофа является следствием закона сохранения заряда и того естественного требования, чтобы при стационарных процессах ни в одной точке проводника не накапливались и не уменьшались заряды. Это правило относится к узлам, то есть к таким точкам в разветвленной цепи, в которой сходится не менее трех проводников.

Первое правило Кирхгофа гласит:

Алгебраическая сумма токов, сходящихся в узле, равна нулю, то есть количество зарядов, приходящих в данную точку цепи в единицу времени, равно количеству зарядов, уходящих из данной точки за то же время

При этом токи, подходящие к узлу и отходящие от него, имеют противоположные знаки (рис. 4.23).

Рис. 4.23. Сумма токов, сходящихся в узле равна нулю

Второе правило Кирхгофа является обобщением закона Ома и относится к любому замкнутому контуру разветвленной цепи.

Второе правило Кирхгофа гласит:

В любом замкнутом контуре цепи алгебраическая сумма произведений токов на сопротивления соответствующих участков контура равна алгебраической сумме ЭДС в контуре (рис. 4.24)

Рис. 4.24. Пример разветвленной электрической цепи.
Цепь содержит один независимый узел (a или d) и два независимых контура (например, abcd и adef)

Правила Кирхгофа позволяют определить силу и направление тока в любой части разветвленной цепи, если известны сопротивления ее участков и включенные в них ЭДС. Число уравнений, составляемых по первому и второму правилам Кирхгофа, должно равняться числу искомых величин. Используя первое правило Кирхгофа для разветвленной цепи, содержащей m узлов и n ветвей (участков), можно написать (m – 1) независимых уравнений, а используя второе правило, (n – m + 1) независимых уравнений.

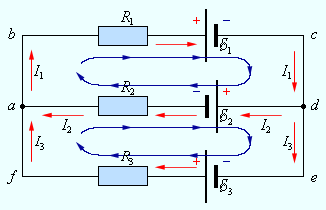
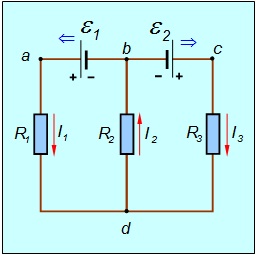
Приведем пример расчета токов в разветвленной цепи (рис. 4.25).

Рис. 4.25. Пример разветвленной цепи

Направления действия ЭДС показаны синими стрелками. В этой цепи у нас имеется два узла — точки b и d (m = 2), и три ветви — участок b–а–d с током I₁, участок b–d с током I₂ и участок b–c–d с током I₃ (n = 3). Значит, мы можем написать одно (m – 1 = 2 – 1 = 1) уравнение на основе первого правила Кирхгофа и два (n – m + 1 = 3 – 2 + 1 = 2) уравнения на основе второго правила Кирхгофа. Как же это делается на практике?

Шаг первый. Выберем направления токов, текущих в каждой из ветвей цепи. Как эти направления выбрать — совершенно неважно. Если мы угадали, в окончательном результате значение этого тока получится положительным, если нет и направление должно быть обратным — значение этого тока получится отрицательным. В нашем примере мы выбрали направления токов как показано на рисунке. Важно подчеркнуть, что направления действия ЭДС не произвольны, они определяются способом подключения полюсов источников тока (см. рис. 4.25).

Шаг второй. Записываем первое правило Кирхгофа для всех узлов кроме одного (в последнем узле, выбор которого произволен, это правило будет выполняться автоматически). В нашем случае мы можем записать уравнение для узла b, куда входит ток I₂ и выходят токи I₁ и I₃

Шаг третий. Нам осталось написать уравнения (в нашем случае — два) для второго правила Кирхгофа. Для этого надо выбрать два независимых замкнутых контура. В рассматриваемом примере имеются три такие возможности: путь по левому контуру b–a–d–b, путь по правому контуру b–c–d–b и путь вокруг всей цепи b–a–d–c–b. Достаточно взять любые два из них, тогда для третьего контура второе правило Кирхгофа будет выполнено автоматически. Направление обхода контура роли не играет, но при обходе ток будет браться со знаком плюс, если он течет в направлении обхода, и со знаком минус, если ток течет в противоположном направлении. Это же относится к знакам ЭДС.

Возьмем для начала контур b–a–d–b. Мы выходим из точки b и движемся против часовой стрелки. На нашем пути встретятся два тока, I₁ и I₂, направления которых совпадают с выбранным направлением обхода. ЭДС 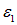также действует в этом же направлении. Поэтому второе правило Кирхгофа для этого участка цепи записывается как

В качестве второго замкнутого пути для разнообразия выберем путь b–a–d–c–b вокруг всей цепи. На этом пути мы встречаем два тока I₁ и I₃, из которых первый войдет со знаком плюс, а второй — со знаком минус. Мы встретимся также с двумя ЭДС, из которых 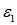войдет в уравнения со знаком плюс, а — со знаком минус. Уравнение для этого замкнутого пути имеет вид

Шаг четвертый. Мы нашли три уравнения для трех неизвестных токов в цепи. Решение произвольной системы линейных уравнений описывается в курсе математики. Для наших целей (цепь достаточна проста) можно просто выразить I₃ через I₁ из уравнения (4.47)

и подставить (4.48), (4.49) в уравнение первого правила Кирхгофа (4.45). Это уравнение содержит лишь неизвестное I₁, которое находится без труда

Подставляя это выражение в (4.48), (4.49), находим соответственно токи I₂, I₃

Шаг пятый. В найденные формулы подставляют численные значения, коль скоро они заданы. Подсчитаем для примера токи в нашей цепи при одинаковых сопротивлениях R₁ = R₂ = R₃ = 10 Ом, но разных ЭДС Имеем:

Последнее значение получилось отрицательным при данных численных характеристиках цепи. Значит, на самом деле направление тока обратно показанному на рисунке. Это естественно: мощный левый источник посылает ток 0,75 А, часть которого (0,45 А) ответвляется в среднюю ветвь, а остаток — 0,3 А — продолжает течь в том же направлении, чему не может воспрепятствовать маломощная правая батарея.

Примечание. Правила Кирхгофа позволяют в принципе рассчитать сколь угодно сложные цепи. Но вычисления могут быть довольно сложными. Поэтому рекомендуется сначала поискать возможную симметрию цепи. Иногда из соображений симметрии более или менее очевидно, что какие-то токи равны между собой или какие-то напряжения равны нулю (и тогда данный участок цепи можно исключить из рассмотрения). Если такое возможно, вычисления существенно упрощаются.

В нашем примере мы пренебрегли внутренним сопротивлением источников тока. При их наличии они также должны включаться в уравнения второго правила Кирхгофа.

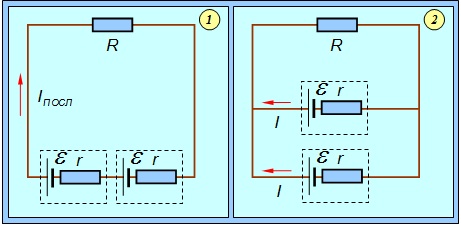
Пример. Два одинаковых источника тока с ЭДС 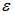и внутренним сопротивлением r соединяются в батарею. Возможны два варианта соединения — последовательное и параллельное (рис. 4.26). При каком соединении ток в нагрузке R будет наибольшим?

Рис. 4.26. Последовательное (1) и параллельное (2) соединение источников тока

Решение. Расчет особенно прост для последовательного соединения: уравнение первого правила Кирхгофа отсутствует, так как в цепи нет узлов. Единственное уравнение второго закона дает

Для упрощения расчета параллельного соединения примем во внимание, что из соображений симметрии токи через источники должны быть равны и совпадать по направлению. Тогда первое правило Кирхгофа дает

Второе правило Кирхгофа, записанное для пути через нижний источник и нагрузку, имеет вид

Отсюда следует, что

Сравнивая (4.53) и (4.56), находим, что при R > r ток последовательной батареи больше (I_посл > I_парал) а при R < r он меньше (I_посл < I_парал) тока от параллельной батареи. При равенстве внутреннего сопротивления и нагрузки R = r обе батареи дают одинаковый ток.

Содержание

Алгоритм составления уравнений
Составляем уравнения по первому закону Кирхгофа
Составляем уравнения по второму закону Кирхгофа
Расчет токов по правилам Кирхгофа
Расчет электрической цепи по закону Кирхгофа
Законы Кирхгофа
Порядок составления уравнений но законам Кирхгофа
Пример задачи с решением 3.2.
📹 Видео

Видео:Как составить уравнения по законам Кирхгофа?Скачать

Алгоритм составления уравнений

Алгоритм составления уравнений по законом Кирхгофа:

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Составляем уравнения по первому закону Кирхгофа

Для составления уравнений по первому закону кирхгофа любой электрической цепи выполняем следующие действия.

Количество уравнений по 1 закону киргофа равно количеству узлов минус один.
Произвольно задаемся направлением токов в каждой ветви электрической цепи.
Если в ветви присутствует источник тока, то считаем данный ток уже известным, равным величине источника тока.
Составляем уравнения по первому правилу Кирхгофа для любых узлов кроме одного.
Расставляем знаки. Токи, которые втекают в узел берем с одним знаком, например с плюсом. Токи, которые вытекают из узла берем с противоположным знаком, например с минусом.

Видео:Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Составляем уравнения по второму закону Кирхгофа

Для составления системы уравнения по 2 правилу Кирхгофа необходимо выполнить следующие пункты.

Количество уравнений по второму закону Киргофа равно количеству независимых контуров. По второму закону можно записать В-В_I-У+1 независимых уравнений. Где В — число ветвей в схеме. В_I— число ветвей в схеме с источником тока. У — число узлов в схеме.
Находим независимые контура в электрической цепи (чтобы отличались хотя бы одной ветвью).
Если в цепи присутствуют источники тока, то данные ветви не учитываем при нахождении независимых контуров.
Задаемся произвольным направление обхода независимых контуров.
Составляем уравнения по второму правилу Кирхгофа для каждого выбранного контура.
Расставляем знаки на участках с нагрузкой. Если направление обхода контура совпадает с направлением протекающего тока, то падение напряжения на заданном участке берем со знаком «+». Если направление протекающего тока не совпадает с направлением обхода контура, то падение напряжения на данном участке берем со знаком «-«.
Расставляем знаки на участках с источниками ЭДС. Если направление действия ЭДС (направление стрелочки) совпадает с направлением обхода независимого контура, то знак будет «плюс». Если не совпадает, то знак — «минус».

Видео:Законы Кирхгофа - самое простое и понятное объяснение этих законовСкачать

Расчет токов по правилам Кирхгофа

Полученные уравнения объединяем в систему уравнений. Количество уравнений должно быть равно количеству неизвестных. Далее решаем систему уравнений любым известным способом.

Правильность расчета проверяется составлением уравнения баланса мощностей.

Видео:Расчет цепи по законам КирхгофаСкачать

Расчет электрической цепи по закону Кирхгофа

Содержание:

Законы Кирхгофа

Уравнения, описывающие поведение электрической цепи, составляют на основе законов Кирхгофа. Они определяют связь между токами и напряжениями элементов, образующих цепь. Уравнения, составленные согласно этим законам, называют уравнениями Кирхгофа.

Первый закон Кирхгофа определяет баланс токов в узлах электрической цепи.

Он формулируется следующим образом:

Алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю:

В уравнении (3.1) токи, направленные от узла, записывают с положительным знаком. Токи, направленные к узлу, записывают со знаком минус.

Система уравнений по первому закону Кирхгофа, записанная для всех узлов цепи, линейно зависима. В этом легко убедиться, сложив все уравнения. Поскольку ток каждой ветви входит в два уравнения с разными знаками, сумма тождественно равна нулю. Поэтому число независимых уравнений по первому закону Кирхгофа равно , где — число узлов цепи.

Второй закон Кирхгофа устанавливает баланс напряжений в контуре цепи:

Алгебраическая сумма напряжений ветвей в контуре равна нулю:

Если напряжение ветви совпадает с направлением обхода контура, то напряжению приписывают знак плюс, если же нет — знак минус. Перенесем напряжения источников напряжения, равные ЭДС этих источников, в правую часть. Уравнение (3.2) примет вид

В соответствии с последним равенством алгебраическая сумма напряжений ветвей в контуре электрической цепи равна алгебраической сумме ЭДС источников.

Число независимых уравнений, записанных по второму закону Кирхгофа, равно числу независимых контуров. Число таких контуров определяется формулой , где — число ветвей.

Возможно вам будут полезны данные страницы:

Порядок составления уравнений но законам Кирхгофа

1. Необходимо сначала выбрать положительные направления токов и напряжений ветвей. Положительное направление тока показывают стрелкой на выводе элемента. Положительное направление напряжения показывают стрелкой, расположенной рядом с элементом. Полярности напряжений резисторов выбирают согласованными с направлениями токов. Направления токов источников напряжения выбирают совпадающими с направлениями ЭДС.

2. Записываем уравнения по первому закону Кирхгофа для узлов.

3. Выбираем направления обхода контуров и записываем уравнения по законам Кирхгофа. Сопротивление проводника, соединяющего элементы, очень мало по сравнению с сопротивлением резистора и игнорируется. Ячейки внутренней цепи удобно выбирать в качестве независимых цепей. Можно воспользоваться и другим способом: выбрать по порядку контуры, так, чтобы каждый следующий контур содержал, по меньшей мере, одну ветвь, не входящую в предыдущие контуры.

4. Решаем полученную систему уравнений и определяем токи и напряжения цепи.

5. После определения токов и напряжений необходимо выполнить проверку. Для этого вычисленные значения переменных подставляют в одно из уравнений, составленных по законам Кирхгофа.

При составлении уравнений в качестве неизвестных рассматривают либо токи, либо напряжения резистивных элементов.

В первом случае уравнения цепи составляют относительно неизвестных токов резистивных элементов и напряжений на источниках тока. Напряжения на резистивных элементах, входящие в уравнения по второму закону Кирхгофа, выражают через токи по закону Ома. Такой способ составления уравнений называют токов ветвей.

Число совместно решаемых уравнений в методе токов ветвей можно сократить, если контуры выбирать так, чтобы они не включали источники тока. В этом случае неизвестными будут только токи резистивных элементов, и по второму закону Кирхгофа достаточно составить уравнений, где — количество источников тока.

Во втором случае уравнения цепи составляются относительно напряжений резистивных элементов и токов источников напряжения. Токи резисторов представляют произведением проводимости на напряжение на резисторе. Этот способ составления уравнений называют методом напряжений ветвей.

В дальнейшем для решения задач мы будем использовать в основном метод токов ветвей.

Пример 3.1. Записать уравнения Кирхгофа для цепи, показанной на рис. 3.1.

Решение. Сначала выберем направления токов резистивных элементов и пронумеруем узлы. Неизвестными являются токи резистивных элементов . Поэтому необходимо составить пять уравнений. Цепь содержит четыре узла; это означает, что по первому закону Кирхгофа можно составить три уравнения. Число уравнений по второму закону Кирхгофа равно двум.

Запишем уравнения по первому закону Кирхгофа для узлов 1, 2, 3. Контуры I и II выберем так, чтобы они не включали источник тока, иначе в системе уравнений появится дополнительная переменная — напряжение источника тока. Направления обхода контуров выберем совпадающими с направлением движения часовой стрелки. В результате получим систему из пяти уравнений с пятью неизвестными токами:

Узел 1: ;

Узел 2: ;

Узел З: ;

Контур I:

Контур II:

Для решения системы уравнений целесообразно использовать математические пакеты, например MathCAD или Matlab.

Напряжение на зажимах источника тока можно затем найти, записав уравнения для контуров, включающих или

Пример задачи с решением 3.2.

Рассчитать токи в цепи, изображенной на рис. 3.2. Номиналы элементов: ,

Решение. Сначала выберем направления токов резистивных элементов и пронумеруем узлы. В рассматриваемой схеме шесть неизвестных токов , следовательно, необходимо составить шесть независимых уравнений. Цепь содержит четыре узла; это означает, что по первому закону Кирхгофа можно составить три уравнения. Еще три уравнения составим по второму закону Кирхгофа. Наличие источника тока учитывалось при определении числа уравнений по второму закону Кирхгофа.

Составим уравнения по первому закону Кирхгофа для узлов 1, 2 и 3. Уравнения по второму закону Кирхгофа запишем для контуров I, II, III. Направление обхода контуров выбираем по часовой стрелке.

В результате получим систему из шести уравнений с шестью неизвестными токами:

В матричной форме записи:

Решением системы уравнений являются следующие значения токов:

Знак минус в численных значениях токов означает, что направление токов при заданных условиях выбрано навстречу истинному.

На странице -> решение задач по электротехнике собраны решения задач и заданий с решёнными примерами по всем темам теоретических основ электротехники (ТОЭ).

Услуги:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.