Число независимых уравнений которое можно записать по первому закону кирхгофа

Видео:Как составить уравнения по законам Кирхгофа?Скачать

Задания. 6.1.Число независимых уравнений, которое можно записать по первому закону Кирхгофа для заданной схемы равно

6.1.Число независимых уравнений, которое можно записать по первому закону Кирхгофа для заданной схемы равно…

а) Пяти б) Четырем в) Трем г) Двум

6.2. Для определения всех токов путем непосредственного применения законов Кирхгофа необходимо записать столько уравнений, сколько ______ в схеме.

а) контуров б) узлов в) сопротивлений г) ветвей

6.3.Математические выражения первого и второго законов Кирхгофа имеют вид…

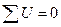
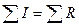
а) и б) и

в) и г) и

6.4. Для данной схемы неверным будет уравнение…

а) б)

в) г)

6.5.Для данной схемы неверным будет уравнение…

а) 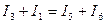б)

в) г)

6.6.Для узла «а» справедливо уравнение …

а) I1+ I2 – I3 – I4=0 б) I1+ I2 + I3 – I4 =0

в) I1 – I2 – I3 – I4 = 0 г) – I1+I2 –I3 – I4=0

6.7.Выражение для второго закона Кирхгофа имеет вид…

а) ∑ I_k = 0 б) U = RI

в) P = I²R г) _mR_m = E_m

6.8.Выражение для первого закона Кирхгофа имеет вид…

а) _mR_m = E_m б) ∑ U_k = 0

6.9.Количество независимых уравнений по первому закону Кирхгофа, необходимое для расчета токов в ветвях составит…

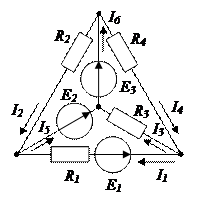а) три б) четыре в) два г) шесть

6.10.Если токи в ветвях составляют I₁= 2 A, I₂ = 10 A, то ток I₅ будет равен…

а) 12 А б) 20 А в) 8 А г) 6 А

6.11.Для контура, содержащего ветви с R₂, R₃, R₅, справедливо уравнение по второму закону Кирхгофа.

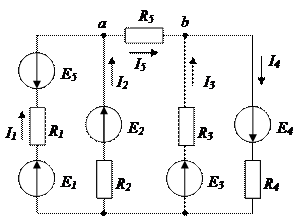
6.12.Для узла «b» справедливо уравнение…

Дата добавления: 2015-04-16 ; просмотров: 39 ; Нарушение авторских прав

Видео:Законы Кирхгофа - самое простое и понятное объяснение этих законовСкачать

Законы Кирхгофа для расчёта электрических цепей

При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие полностью определить режим её работы.

Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.

Прежде чем перейти к самим законам Кирхгофа, дадим определение ветвей и узлов электрической цепи.

Ветвью электрической цепи называется такой её участок, который состоит только из последовательно включённых источников ЭДС и сопротивлений, вдоль которого протекает один и тот же ток. Узлом электрической цепи называется место (точка) соединения трёх и более ветвей. При обходе по соединённым в узлах ветвям можно получить замкнутый контур электрической цепи. Каждый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза [1].

Первый закон Кирхгофа

Первый закон Кирхгофа применяется к узлам и формулируется следующим образом: алгебраическая сумма токов в узле равна нулю:

или в комплексной форме

Второй закон Кирхгофа

Второй закон Кирхгофа применяется к контурам электрической цепи и формулируется следующим образом: в любом замкнутом контуре алгебраическая сумма напряжений на сопротивлениях, входящих в этот контур, равна алгебраической сумме ЭДС:

Количество уравнений, составляемых для электрической цепи по первому закону Кирхгофа, равно $ N_textrm-1 $, где $ N_textrm $ – число узлов. Количество уравнений, составляемой для электрической цепи по второму закону Кирхгофа, равно $ N_textrm-N_textrm+1 $, где $ N_textrm $ – число ветвей. Количество составляемых уравнений по второму закону Кирхгофа легко определить по виду схемы: для этого достаточно посчитать число «окошек» схемы, но с одним уточнением: следует помнить, что контур с источником тока не рассматривается.

Опишем методику составления уравнений по законам Кирхгофа. Рассмотрим её на примере электрической цепи, представленной на рис. 1.

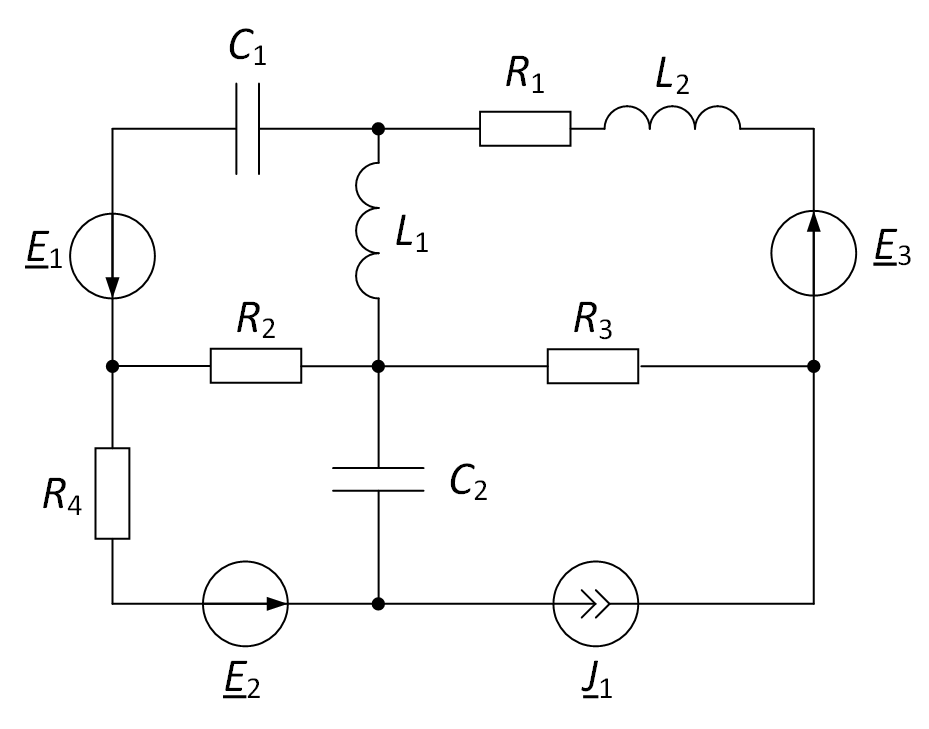
Рис. 1. Рассматриваемая электрическая цепь

Для начала необходимо задать произвольно направления токов в ветвях и задать направления обхода контуров (рис. 2).

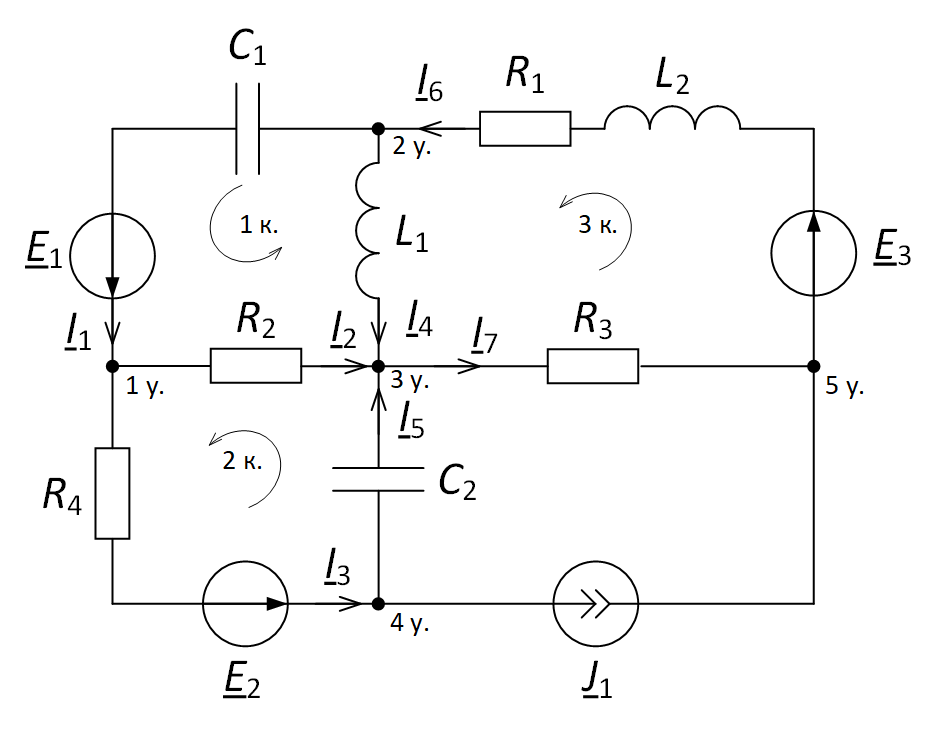
Рис. 2. Задание направления токов и направления обхода контуров для электрической цепи

Количество уравнений, составляемых по первому закону Кирхгофа, в данном случае равно 5 – 1 = 4. Количество уравнений, составляемых по второму закону Кирхгофа, равно 3, хотя «окошек» в данном случае 4. Но напомним, что «окошко», содержащее источник тока $ underline_ $, не рассматривается.

Составим уравнения по первому закону Кирхгофа. Для этого «втекающие» в узел токи будем брать со знаком «+», а «вытекающие» — со знаком «-». Отсюда для узла «1 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

$$ underline_- underline_- underline_ = 0; $$

для узла «2 у.» уравнение по первому закону Кирхгофа будет выглядеть следующим образом:

$$ -underline_- underline_ + underline_ = 0; $$

$$ underline_+ underline_ + underline_- underline_ = 0; $$

$$ underline_- underline_- underline_ = 0. $$

Уравнение для узла «5 у.» можно не составлять.

Составим уравнения по второму закону Кирхгофа. В этих уравнениях положительные значения для токов и ЭДС выбираются в том случае, если они совпадают с направлением обхода контура. Для контура «1 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

$$ underline_ cdot underline_ + R_ cdot underline_- underline_ cdot underline_ = underline_; $$

для контура «2 к.» уравнение по второму закону Кирхгофа будет выглядеть следующим образом:

$$ -R_ cdot underline_ + R_ cdot underline_ + underline_ cdot underline_ = underline_; $$

для контура «3 к.»:

$$ underline_ cdot underline_ + (underline_ + R_) cdot underline_ + R_ cdot underline_ = underline_; $$

где $ underline_ = -frac $, $ underline_ = omega L $.

Таким образом, для того, чтобы найти искомые токи, необходимо решить следующую систему уравнений:

$$ begin underline_- underline_- underline_ = 0 \ -underline_- underline_ + underline_ = 0 \ underline_+ underline_ + underline_- underline_ = 0 \ underline_- underline_- underline_ = 0 \ underline_ cdot underline_ + R_ cdot underline_- underline_ cdot underline_ = underline_ \ -R_ cdot underline_ + R_ cdot underline_ + underline_ cdot underline_ = underline_ \ underline_ cdot underline_ + (underline_ + R_) cdot underline_ + R_ cdot underline_ = underline_ end $$

В данном случае это система из 7 уравнений с 7 неизвестными. Для решения данной системы уравнений удобно пользоваться Matlab. Для этого представим эту систему уравнений в матричной форме:

$$ begin 1 & -1 & -1 & 0 & 0 & 0 & 0 \ -1 & 0 & 0 & -1 & 0 & 1 & 0 \ 0 & 1 & 0 & 1 & 1 & 0 & -1 \ 0 & 0 & 1 & 0 & -1 & 0 & 0 \ underline_ & R_ & 0 & -underline_ & 0 & 0 & 0 \ 0 & -R_ & R_ & 0 & underline_ & 0 & 0 \ 0 & 0 & 0 & underline_ & 0 & R_+underline_ & R_ \ end cdot begin underline_ \ underline_ \ underline_ \ underline_ \ underline_ \ underline_ \ underline_ \ end = begin 0 \ 0 \ 0 \ underline_ \ underline_ \ underline_ \ underline_ \ end $$

Для решения данной системы уравнений воспользуемся следующим скриптом Matlab:

В результате получим вектор-столбец $ underline<bold> $ токов из семи элементов, состоящий из искомых токов, записанный в общем виде. Видим, что программный комплекс Matlab позволяет существенно упростить решение сложных систем уравнений, составленных по законам Кирхгофа.

Список использованной литературы

1. Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.

Рекомендуемые записи

При расчёте электрических цепей, помимо законов Кирхгофа, часто применяют метод контурных токов. Метод контурных токов…

Расчёт матриц передачи многополюсников различной формы осуществляется достаточно просто. Матрицы передачи — это математическое описание рассматриваемой…

Добавить комментарий Отменить ответ

Для отправки комментария вам необходимо авторизоваться.

Этот сайт использует Akismet для борьбы со спамом. Узнайте, как обрабатываются ваши данные комментариев.

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Алгоритм составления уравнений

Алгоритм составления уравнений по законом Кирхгофа:

Видео:Применение законов Кирхгофа при решении задачСкачать

Составляем уравнения по первому закону Кирхгофа

Для составления уравнений по первому закону кирхгофа любой электрической цепи выполняем следующие действия.

1. Количество уравнений по 1 закону киргофа равно количеству узлов минус один.
2. Произвольно задаемся направлением токов в каждой ветви электрической цепи.
3. Если в ветви присутствует источник тока, то считаем данный ток уже известным, равным величине источника тока.
4. Составляем уравнения по первому правилу Кирхгофа для любых узлов кроме одного.
5. Расставляем знаки. Токи, которые втекают в узел берем с одним знаком, например с плюсом. Токи, которые вытекают из узла берем с противоположным знаком, например с минусом.

Видео:Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Составляем уравнения по второму закону Кирхгофа

Для составления системы уравнения по 2 правилу Кирхгофа необходимо выполнить следующие пункты.

1. Количество уравнений по второму закону Киргофа равно количеству независимых контуров. По второму закону можно записать В-В_I-У+1 независимых уравнений. Где В — число ветвей в схеме. В_I— число ветвей в схеме с источником тока. У — число узлов в схеме.
2. Находим независимые контура в электрической цепи (чтобы отличались хотя бы одной ветвью).
3. Если в цепи присутствуют источники тока, то данные ветви не учитываем при нахождении независимых контуров.
4. Задаемся произвольным направление обхода независимых контуров.
5. Составляем уравнения по второму правилу Кирхгофа для каждого выбранного контура.
6. Расставляем знаки на участках с нагрузкой. Если направление обхода контура совпадает с направлением протекающего тока, то падение напряжения на заданном участке берем со знаком «+». Если направление протекающего тока не совпадает с направлением обхода контура, то падение напряжения на данном участке берем со знаком «-«.
7. Расставляем знаки на участках с источниками ЭДС. Если направление действия ЭДС (направление стрелочки) совпадает с направлением обхода независимого контура, то знак будет «плюс». Если не совпадает, то знак — «минус».

Видео:Урок 14. Законы Кирхгофа простыми словами с примерамиСкачать

Расчет токов по правилам Кирхгофа

Полученные уравнения объединяем в систему уравнений. Количество уравнений должно быть равно количеству неизвестных. Далее решаем систему уравнений любым известным способом.

Правильность расчета проверяется составлением уравнения баланса мощностей.

🌟 Видео

Первый закон Кирхгофа! Хочешь понять? Посмотри!Скачать

Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Метод контурных токов - определение токов. ЭлектротехникаСкачать

Урок 265. Задачи на правила КирхгофаСкачать

решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Лекция 020-1. Цепи постоянного тока. Расчет при помощи уравнений КирхгофаСкачать

Лекция 010-3. Основные законы электрических цепей - законы КирхгофаСкачать

Правила Кирхгофа - определение токов. ЭлектротехникаСкачать

Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Метод узловых и контурных уравненийСкачать

Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 1 часть. 6 класс.Скачать