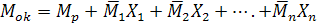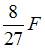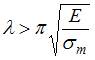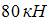Число канонических уравнений которое необходимо составить и решить для раскрытия

Видео:Дробно-рациональные уравнения. 8 класс.Скачать

РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ МЕТОДОМ СИЛ

Общие сведения

Расчет статически неопределимых систем методом сил начинают с вы­явления степени статической неопределимости. Степень статической не­определимости любой системы может быть установлена по формуле, которая для выявления степени статической неопределимости рам будет иметь вид:

где Л – число лишних связей, К – число контуров, а для неразрезных балок — формулой (24):

где С_оп — число опорных стержней.

Остановимся на применении формулы (23).

Пример 7.1.

Пользуясь формулой (23), опреде­лить степень статической неопределимости рамы, изображенной на рис. 7.1.

Решение

Рама состоит из двух замкнутых контуров I и II. Шарнирно-неподвижная опора А равноценна одному простому шарниру, шарнирно-подвижная опора В — двум шарнирам. Следова­тельно, Ш= 1 + 2 = 3.

Степень статической неопределимости Л = 3К — Ш=3∙2 — 3 ==3 — рама трижды ста­тически неопределима.

Пример 7.2.

Определить степень статической неопределимости рамы, приведенной на рис. 7.2.

Рис. 7.2. 3-х контурная рама. Рис. 7.3. 6-ти контурная рама

Решение

Рама имеет три замкнутых контура (I, II и III). Сум­марное число шарниров Ш = 6 (два простых шарнира — Е и F и две шарнирно подвижные опоры —A и D). Число лишних связей Л =3∙3 — 6=3. Следовательно, рама трижды статически неопределима.

Пример 7.3.

Определить степень статической неопределимости рамы, изображённой на рис. 7.3.

Решение

В этой раме шесть замкнутых контуров. Простых шар­ниров — три (шарниры F,H и I). Шарнир G— двукратный, как соединяю­щий три стержня. Каждая из шарнирно-подвижных опор А, В, D и Е эквивалентна двум простым шарнирам, а шарнирно-неподвижная опора С — одному. Следовательно, Ш = 1∙3 + 2∙1 + 2∙4 + 1 =14. Тогда степень статической неопределимости Л =3∙6—14 =4. Таким образом, рама имеет четыре лишние связи, т. е. является четырежды статически неопределимой.

После того как будет установлена степень статической неопределимости, выбирают основную систему.

Выбор основной системы

Основной системой будем называть геометрически неизме­няемую статически определимую систему, полученную из заданной стати­чески неопределимой путем устранения лишних связей и нагрузки.

На рис. 7.4., а показана статически неопределимая рама — заданная система. Степень статической неопределимости этой системы:

Следовательно, чтобы из заданной системы получить основную систему, надо освободить раму от нагрузки q и отбросить три лишние связи; по­следнее может быть выполнено различными способами, но в результате применения любого из них полученная основная система должна быть геометрически неизменяемой.

Так, например, на рис. 7.4., б показана основная система, полученная путем устранения нагрузки q и правой защемляющей опоры В, эквивалент­ной трем лишним связям.

Рис. 7.4. Выбор основной системы

Теперь сечение В основной системы может перемещаться по горизонталь­ному и вертикальному направлениям и поворачиваться в плоскости рамы на некоторый угол, т. е. в основной системе стали возможными те перемещения, которым в заданной системе препятствует правая защемляющая опора.

Чтобы устранить различие между заданной и основной системами, поступим так, как показано на рис. 7.4., в: нагрузим основную систему заданной нагрузкой q и вточке В ее, по направлениям указанных переме­щений сечения В, приложим соответствующие им пока неизвестные, горизонтальную и вертикальную силы Х₁; Х₂ и момент Х₃.

Величины Х₁; Х₂; X₃ называются лишними неизвестными и являются искомыми реакциями лишних связей, заменяющими действие отброшен­ных лишних связей на заданную систему.

Обращаем внимание, на то, что основная система, нагружен­ная заданной нагрузкой и лишними неизвестными, в отношении внут­ренних усилий и перемещений эквивалентна заданной статически неопре­делимой.

Кроме того, условимся в дальнейшем, как это принято в практических расчетах, основную систему на отдельном рисунке не изображать и взамен ее приводить рисунок выбранной основной системы, нагруженной задан­ной нагрузкой и лишними неизвестными.

Далее составляют уравнения совместности перемещений, каждое из которых должно выражать условие равенства нулю суммарного пере­мещения по направлению той или иной, отброшенной связи (неизвестной силы) от заданной нагрузки и всех лишних неизвестных. Эти уравнения, написанные в определенной, раз навсегда установленной форме, называют каноническими уравнениями метода сил. Число их должно равняться числу отброшенных связей. Для рассматриваемой рамы необходимо составить, таким образом, три канонических уравнения, имеющих следующий вид:

где δ₁₁ —перемещение точки приложения силы X₁ по направлению этой силы от единичной силы = 1;

δ₁₁ X₁ —перемещение той же точки в том же направлении, вызванное полным значением X₁;

δ₁₂ — перемещение точки приложения силы X₁ по направлению этой силы, вызванное единич­ной силой

δ₁₂ X₂ — перемещение той же точки в том же направле­нии, вызванное полным значением силы Х₂;

δ₁₃ — перемещение точки приложения силы Х_х по направлению этой силы от единичной силы = 1;

δ₁₃X₃ — перемещение той же точки в том же направлении, вызван­ное полным значением силы Х₃;

∆_1p —перемещение той же точки в том же направлении, вызванное заданной нагрузкой; δ₂₁ X₁ — перемещение точки приложения силы Х₂ по направлению этой силы, вызванное силой X₁, и т. д.

Следует иметь в виду, что один раз составленные в общем виде п канонических уравнений с п неизвестными применимы для любой п раз стати­чески неопределимой системы. Так, уравнения (25) справедливы для любой трижды статически неопределимой системы.

Составив канонические уравнения метода сил, следует перейти к вы­числению единичных δ_ik и грузовых ∆_ip перемещений.

Для этого предварительно введем понятия о грузовом и единичном состояниях основной системы.

Грузовым назовем то состояние основной системы, при котором она находится только под действием заданной нагрузки.

Единичнымбудем называть состояние основной системы, при ко­тором она нагружена только одной силой, равной единице е = 1, дейст­вующей в направлении неизвестной реакции X_t.

Заметим, что число единичных состояний основной системы должно соответствовать степени статической неопределимости заданной системы,

т. е. числу лишних неизвестных. Изобразив на рисунках грузовое и отдельно все единичные состояния основной системы, строят соответствующие им грузовую М_р и единичные M₁, M₂, . М_п эпюры изгибающих моментов.

Наконец, используя способ перемножения эпюр, вычисляют единич­ные δ_ik и грузовые ∆_ip перемещения.

Перемножая эпюры, следует помнить, что на основании теоремы о взаимности пере­мещений (теоремы Максвелла) единичные перемещения с взаимно пере­ставленными индексами равны между собой, т. е. δ_ik = δ_ki.

Вычисленные значения δ_ik и ∆_ip подставляют в канонические уравнения и решают полученную систему уравнений, в результате чего нахо­дят значения неизвестных реакций связей X₁, X₂, . Х_п.

Нагрузив те­перь основную систему заданной нагрузкой и уже известными силами X₁ = А₁;Х₂ = А₂, . Х_п = А_п, строят обычным путем (как для статиче­ски определимой системы) эпюры Q, М и N, которые и являются оконча­тельными эпюрами поперечных сил, изгибающих моментов и продольных сил для заданной системы.

Окончательную эпюру изгибающих моментов можно также получить путем суммирования ординат эпюры М_р с соответствующими ординатами эпюры

После определения неизвестных можно сразу получить эпюру М, по которой построить эпюру Q, а продольные силы определить из условий равновесия вырезаемых узлов рамы. Опорные реакции в этом случае находят в последнюю очередь, используя эпюры Q, М и N,

умноженными на X₁, ординатами эпюры , умноженными на Х₂ . и ординатами эпюры , умноженными на Х_п, т. е.

Единичные перемещения с одинаковыми индексами (δ₁₁, δ₂₂, δ₃₃ и т.д.) принято называть главными перемещениями, а с разными индексами

Главные перемещения никогда не обращаются в нуль и всегда имеют положительное значение, так как в этом случае эпюры умножаются сами на себя, т. е. и площадь ω и ордината у берутся из одной и той же эпюры.

Побочные перемещения могут быть положительными, отрицательными, а при удачном выборе основной системы и равными нулю. В последнем случае в значительной мере сокращаются и упрощаются операции по вы­числению перемещений.

На рис. 7.4., б основная система выбрана неудачно, так как для нее ни одно из побочных перемещений не обратится в нуль. Ниже эта рама будет рассчитана, при более рациональном выборе основной системы.

Видео:Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

Выберите неправильное определение понятия степени статической неопределимости

Число связей, при котором достигается кинематическая неизменяемость системы, носит название_______ связей.

3) необходимого числа

Выберите неправильное определение понятия степени статической неопределимости.

1) Количество дополнительных внутренних связей, наложенных на систему сверх необходимого для достижения ее кинематической неизменяемости.

2) Количество внешних и внутренних связей, наложенных на систему сверх необходимых.

3) Разница между числом неизвестных (реакций опор и внутренних силовых факторов) и числом независимых уравнений статики, которые могут быть составлены для рассматриваемой системы.

4) Суммарное количество дополнительных внутренних и внешних связей

4 Степень статической неопределимости плоской рамы…

5 Степень статической неопределимости плоской балки равна …

6 Степень статической неопределимости для плоского замкнутого контура равна…

**27 Статически неопределимые системы / Метод сил

1 Число канонических уравнений, которое нужно составить и решить для раскрытия статической неопределимости, равно…

2 На рисунке показана плоская, статически неопределимая рама и четыре варианта основной системы метода сил. Правильный ответ соответствует варианту.

1)

2)

3)

4)

3 Для плоской статически неопределенной рамы выбрана основная система метода сил и записаны канонические уравнения. Неправильным является следующее определение коэффициентов канонических уравнений:

1) – это перемещение по направлению силы под действием единичной силы, заменяющей силу F.

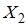
2) – это перемещение по направлению силы под действием единичной силы, заменяющей силу .

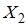
3) – это перемещение по направлению силы под действием единичной силы, заменяющей силу .

4) – это перемещение по направлению силы под действием единичной силы, заменяющей силу .

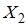
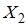
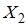
4 Система канонических уравнений имеет вид . Произведение – это перемещение по направлению …

1) i-го силового фактора под действием единичной силы, заменяющей k-й фактор

2) i-го силового фактора от неизвестной k-ой силы

3) k-го силового фактора от внешних сил

4) i-го силового фактора от заданной внешней нагрузки

5 Для заданной статически неопределимой балки представлены четыре варианта основной системы метода сил. Неправильный ответ соответствует варианту.

1)

2)

3)

4)

6 Система, освобожденная от дополнительных связей, статически определимая и кинематически неизменяемая, носит название…

1) основной системы

2) эквивалентной системы

3) системы с определенным числом степеней свободы

4) расчетной схемы

**28 Статически неопределимые системы / Расчет простейших статически неопределимых систем

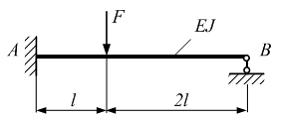
1 Для балки, представленной на рисунке, реакция опоры В равна…

1)

3)

4)

2 Стержень нагружен силой F. Модуль упругости материала Е, площадь поперечного сечения А, размер известны. Наибольшее нормальное напряжение равно…

1)

2)

3)

4)

3 Стержень круглого сечения диаметром работает на деформацию кручение. Модуль сдвига материала , размер , значение заданы. Наибольшее касательное напряжение равно…

1)

2)

3)

4)

4 Если 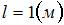, , величина момента в заделке А равна …

1)

3)

4)

5 Поперечное сечение плоской рамы − квадрат. Модуль упругости материала Е, значение силы F, размер b заданы. Наибольшее нормальное напряжение в раме равно… (Влиянием продольной силы пренебречь)

1)

2)

3)

4)

6 Если , реакция опоры С для представленной плоской рамы равна …

1)

2)

3)

4)

**29 Устойчивость сжатых стержней / Устойчивое и неустойчивое упругое равновесие. Критическая сила. Критическое .

1 Формула для определения гибкости стержня длиной l имеет вид…

1)

2)

3)

4)

2 На рисунках показаны схемы нагружения стержня силой F. Стержень может потерять устойчивость на рисунке …

3 Свойство системы сохранять свое состояние при внешних воздействиях называется…

4 Критическая сила сжатого стержня – …

1) величина осевой сжимающей силы, при которой происходит существенный рост деформаций без заметного увеличения самой силы

2) наименьшее значение осевой сжимающей силы, способной удержать стержень в изогнутом состоянии

3) наименьшее значение осевой сжимающей силы, при которой напряжения достигают допускаемой величины

4) значение осевой сжимающей силы, превышение которой вызывает отклонение от закона Гука

5 Число, показывающее, во сколько раз следует изменить длину шарнирно-опертого стержня, чтобы критическая сила для него равнялась критической силе стержня длиной l при рассматриваемых условиях закрепления, называется коэффициентом …

2) запаса на устойчивость

3) приведения длины

4) масштабного фактора

6 Стержень круглого сечения диаметром нагружен внешней силой . Модуль упругости материала , длина . Значение критического напряжения равно… (При расчете принять )

1)

2)

3)

4)

**30 Устойчивость сжатых стержней / Формула Эйлера для критической силы сжатого стержня и пределы ее применимости

1 Использование формулы Эйлера является корректным при выполнении неравенства …

1)

2)

3)

4)

2 Обобщенная формула для определения критической силы сжатого стержня имеет вид…

1)

2)

3)

4)

3 Стержень круглого сечения диаметром нагружен силой . При увеличении диаметра в два раза значение критической силы увеличится в ________ раз (-а).
При решении учитывайте, что нормальные напряжения в стержне не превышают предела пропорциональности.

4) 8
4 Стержни изготовлены из одного материала, имеют одинаковую длину, размеры и форму поперечного сечения. Критическая сила имеет наибольшее значение для стержня, показанного на рисунке…
При решении учитывайте, что напряжения в стержнях не превышают предел пропорциональности.

5 Стержень длиной на одном конце жестко защемлен, другой конец − свободен. Модуль упругости материла , предел пропорциональности , размер . Значение критической силы равно … (При вычислениях принять )

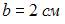
1)

2)

3)

4)

6 Граница применимости обобщенной формулы Эйлера определяется.

1) неравенством

2) неравенством

3) величиной жесткости поперечного сечении стержня на изгиб

4) физико-механическими свойствами материала сжимаемого стержня .

*31 Устойчивость сжатых стержней / Влияние условий закрепления концов стержня на величину критической силы

1 На рисунке показаны два варианта закрепления одинаковых стержней. Отношение значений критических напряжений равно … (При решении учитывайте, что напряжения в стержнях не превышают предела пропорциональности).

1)

2)

2 При установке шарнирно-подвижной опоры в середине длины стержня АВ критическая сила…

1) увеличится в 16 раз

2) увеличится в 4 раза

3) увеличится в 2 раза

3 Одинаковые стержни закреплены, как показано на рисунках. Гибкость будет наименьшей для стержня, показанного на рисунке…

4 Если удалить опору В, то величина критической силы…

1) уменьшится в 2 раза

2) уменьшится в 16 раз

3) уменьшится в 4 раза

5 Коэффициент приведения длины сжатого стержня зависит от…

1) площади поперечного сечения стержня

2) длины стержня

3) модуля упругости материала стержня

4) условий закрепления стержня

6 При замене жестких закреплений стержня на шарнирные, значение критической силы…
При решении учитывайте, что напряжения в стержнях не превышают предел пропорциональности.

1) уменьшится в 2 раза

2) увеличится в 4 раза

3) уменьшится в 8 раз

4) уменьшится в 4 раза

**32 Устойчивость сжатых стержней / Устойчивость за пределом пропорциональности. Расчет сжатых стержней на .

1 График зависимости критического напряжения от гибкости, когда напряжение в стержне не превышает предела пропорциональности, имеет вид…

4) квадратной параболы

2 Длина стержня . Поперечное сечение – квадрат со стороной . Допускаемое напряжение на сжатие . Допускаемое напряжение на устойчивость равно…

1)

2)

3)

4)

3 Условия закрепления стержня одинаковы во всех плоскостях, проходящих через его ось. Варианты поперечных сечений, которые имеют одинаковую площадь, показаны на рисунках. Наиболее рациональной, с точки зрения устойчивости, будет форма поперечного сечения, представленная на рисунке…

3) в Не очевидно, так как не ясны пропорции «двутавра»

4 Материал стержня − сталь 3 (модуль упругости , предел пропорциональности , предел текучести ). Формула Ясинского применима при значениях…

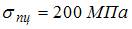
1)

2)

3)

4)

5 Допускаемое напряжение на устойчивость связано с допускаемым напряжением на сжатие зависимостью . Коэффициент пропорциональности называется …

1) коэффициентом приведения длины

2) коэффициентом снижения основного допускаемого напряжения

3) коэффициентом запаса на устойчивость

4) теоретическим коэффициентом концентрации напряжений

6 Стержень длиной закреплен, как показано на рисунке. Площадь поперечного сечения , минимальный момент инерции поперечного сечения , модуль упругости материала стержня , предел пропорциональности , предел текучести Значение критической силы для сжатого стержня равно…

1) 2,188 Мн.

1) Определяем значение предельной гибкости стержня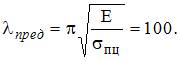
2) Найдем гибкость из уравнения
, откуда =61.
3) Определяем гибкость данного стержня , где , п – количество полуволн упругой линии изогнутого стержня.
.
4) Из условия, что гибкость данного стержня находится в пределах от 100 до 61, при определении значения критической силы используем формулу Ясинского
Мн.

Видео:Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Число канонических уравнений которое необходимо составить и решить для раскрытия

Наиболее широко применяемым в машиностроении общим методом раскрытия статической неопределимости стержневых и рамных систем является метод сил. Он заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так и взаимных, а их действие заменяется силами и моментами. Величина их в дальнейшем подбирается так, чтобы перемещения в системе соответствовали тем ограничениям, которые накладываются на систему отброшенными связями. Таким образом, при указанном способе решения неизвестными оказываются силы. Отсюда и название «метод сил». Такой прием не является единственно возможным. В строительной механике широко применяются и другие методы, например метод деформаций, в котором за неизвестные принимаются не силовые факторы, а перемещения в элементах стержневой системы.

Итак, раскрытие статической неопределимости любой рамы методом сил начинается с отбрасывания дополнительных связей. Система, освобожденная от дополнительных связей, становится статически определимой. Она носит название основной системы.

а-д) модификации основной системы
Рис.1. пример стержневой рамы:

Для каждой статически неопределимой стержневой системы можно подобрать, как правило, сколько угодно основных систем. Например, для рамы, показанной на рис. 1, можно предложить основные системы, а), б). которые получены путем отбрасывания семи дополнительных связей в различных комбинациях. Вместе с тем нужно помнить, что не всякая система с семью отброшенными связями может быть принята как основная. На рис. 2 показано три примера для той же рамы, в которой также отброшено семь связей, однако сделано это неправильно, так как оставшиеся связи не обеспечивают кинематической неизменяемости системы, с одной стороны, и статической определимости во всех узлах,— с другой.

Рис.2.Некорректные преобразования заданной системы в основные по причине кинематической изменяемости- а) б), или статической определимости во всех узлах — в)

После того как дополнительные связи отброшены и система превращена в статически определимую, необходимо, как уже говорилось, ввести вместо связей неизвестные силовые факторы. В тех сечениях, где запрещены линейные перемещения, вводятся силы. Там, где запрещены угловые смещения, вводятся моменты. Как в том, так и в другом случае неизвестные силовые факторы будем обозначать X_i-, где i — номер неизвестного. Наибольшее значение i равно степени статической неопределимости системы. Заметим, что для внутренних связей силы X_i, — являются взаимными. Если в каком-либо сечении рама разрезана, то равные и противоположные друг другу силы и моменты прикладываются как к правой, так и к левой частям системы.

а)-д) по отношению к заданной системе
Рис.3. Пять разновидностей основных систем

Основная система, к которой приложены все внешние заданные силы и неизвестные силовые факторы, носит название эквивалентной системы. На рис. 3 показано пять эквивалентных систем, которые соответствуют приведенным выше основным системам (рис. 1). Принцип приложения неизвестных силовых факторов становится ясным без дальнейших пояснений.

Теперь остается составить уравнения для определения неизвестных.

Обратимся к некоторому конкретному примеру. Рассмотрим, например, первую эквивалентную систему из числа представленных на рис. 3,4. Тем, что рассматривается конкретно взятая семь раз статически неопределимая система, общность рассуждений не будет нарушена.

Перейдем теперь к составлению уравнений для определения неизвестных силовых факторов. Условимся через обозначать взаимное смещение точек системы.

Рис.4. Пример расчета рамы а)по выбранной основной системе- б)

Первый индекс при соответствует направлению перемещения, а второй — силе, вызвавшей это перемещение.

В рассматриваемой раме в точке А отброшена неподвижная опора. Следовательно, горизонтальное перемещение здесь равно нулю и можно записать:

Индекс 1 означает, что речь идет о перемещении по направлению силы Х₁, а индекс [Х₁, Х₂. Р] показывает, что перемещение определяется суммой всех сил, как заданных, так и неизвестных.

Аналогично можно записать:

Так как под величиной понимается взаимное смещение точек, то обозначает вертикальное смещение точки В относительно С, — горизонтальное взаимное смещение тех же точек, есть взаимное угловое смещение сечений В и С. Угловым смещением будет также в рассматриваемой системе величина .

В точках A и D смещения являются абсолютными. Но абсолютные смещения можно рассматривать как смещения, взаимные с неподвижными отброшенными опорами. Поэтому принятые обозначения приемлемы для всех сечений системы.

Пользуясь принципом независимости действия сил, раскроем выражения для перемещений

Аналогичным образом запишем и остальные пять уравнений: каждое из слагаемых , входящих в уравнение, обозначает перемещение в направлении силы с первым индексом под действием силы, стоящей во втором индексе. Поскольку каждое перемещение пропорционально соответствующей силе, величину можно записать в следующем виде:

Что касается перемещений , и т. д., то под индексом Р будем понимать не просто внешнюю силу Р, а вообще систему внешних сил, которая может быть произвольной Поэтому величины , . в уравнениях оставим неизменными.

Теперь уравнения примут вид:

Эти уравнения являются окончательными и носят название канонических уравнений метода сил. Число их равно степени статической неопределимости системы. В некоторых случаях, как увидим далее, когда имеется возможность сразу указать значения некоторых неизвестных, число совместно решаемых уравнений снижается. Остается теперь выяснить, что представляют собой коэффициенты и как следует их определять. Для этого обратимся к выражению (6.1).

Если , то

Следовательно, коэффициент это есть перемещение по направлению i-го силового фактора под действием единичного фактора, заменяющего k-й фактор. Например, коэффициент уравнения представляет собой взаимное горизонтальное смещение точек B и С, которое возникло бы в раме, если бы к ней вместо всех сил была приложена только единичная сила в точке А (рис. 5 а). Если, например, вместо сил приложив единичные силы, а все прочие силы с эквивалентной системы снять (рис. 5 б), то угол поворота в сечении D под действием этих сил будет , горизонтальное перемещение в точке А будет и т. д.

а) , б) и
Рис.5. Интерпретация коэффициентов уравнений метода сил:

Весьма существенно отметить, что в проделанном выводе совершенно не обусловливается то, каким образом возникают перемещения . Хотя мы и рассматриваем раму, работающую на изгиб, все сказанное с равным успехом может быть отнесено, вообще, к любой системе, работающей на кручение, растяжение и изгиб или на то, другое и третье совместно.

Обратимся к интегралам Мора. Для того чтобы определить величину , следует вместо внешних сил рассматривать единичную силу, заменяющую k-й фактор. Поэтому внутренние моменты и силы , , , , и в интегралах Мора заменим на , , , , и , понимая под ними внутренние моменты и силы от единичного k-го фактора. В итоге получим:

где , — внутренние моменты и силы, возникающие под действием i-го единичного фактора. Таким образом, коэффициенты получаются как результат перемножения i-го и k-го внутренних единичных силовых факторов. Индексы i и k непосредственно указывают, какие факторы должны быть перемножены под знаком интегралов Мора. Если рама состоит из прямых участков и можно пользоваться правилом Верещагина, то представляет собой результат перемножения i-х единичных эпюр на k-е единичные эпюры.

Это следует, с одной стороны, непосредственно из выражений для , а с другой стороны, из теоремы о взаимности перемещений, поскольку перемещения и возникают под действием одной и той же силы, равной единице.

Величины , входящие в канонические уравнения, представляют собой перемещения в направлениях 1, 2. возникающие под действием заданных внешних сил в эквивалентной системе. Они определяются перемножением эпюры моментов заданных сил на соответствующие единичные эпюры.

Пример Раскрыть статическую неопределимость и построить эпюру изгибающих моментов для рамы, показанной на рис. 6.

Рис.6. Заданная расчетная схема

Рама три раза статически неопределима. Выбираем основную систему, отбрасывая левую заделку. Действие заделки заменяем двумя силами , и моментом и определяем эквивалентную систему (рис. 7).

Рис.7. Динамика решения: от эквивалентной системы и силовой эпюры Р, включая эпюры моментов от единичных сил: 1, 2, 3 в точках приложения неизвестных , ,

Канонические уравнения (6.2) принимают для рассматриваемой системы такой вид:

Основные перемещения в рассматриваемой раме определяются изгибом. Поэтому, пренебрегая сдвигом и сжатием стержней, строим эпюры изгибающих моментов от заданной силы P и от трех единичных силовых факторов (рис. 7).

Определяем коэффициенты уравнений, считая, что жесткость на изгиб всех участков рамы постоянна и равна EJ. Величина определяется перемножением первой единичной эпюры самой на себя. Для каждого участка берется, следовательно, площадь эпюры и умножается на ординату этой же эпюры, проходящую через ее центр тяжести:

Заметим, что величины при всегда положительны, поскольку площади эпюр и ординаты имеют общий знак.

Определяем, далее, и остальные коэффициенты уравнений, перемножая эпюры с соответствующими номерами:

, , , , , , , .

Подставляем найденные коэффициенты в канонические уравнения. После сокращений получаем:

, ,

Решая эти уравнения, находим:

, ,

Раскрытие статической неопределимости на этом заканчивается.

Рис.8. Суммарная эпюра изгибающих моментов.

Эпюра изгибающих моментов может быть получена наложением на эпюру моментов заданных сил трех единичных эпюр, увеличенных соответственно в , и раза Суммарная эпюра изгибающих моментов представлена на рис. 8. Там же пунктиром показана форма изогнутой оси рамы.

Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

ПроСопромат.ру

Видео:Линейное уравнение с одной переменной. 6 класс.Скачать

Технический портал, посвященный Сопромату и истории его создания

Видео:Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Статически неопределимые балки и рамы (метод сил)

Метод сил

Статически неопределимые — это такие балки и рамы, в которых для определения всех опорных реакций и внутренних усилий уравнений статики не хватает, то есть это система с «лишними» связями. «Лишние» (избыточные) связи бывают внешними, бывают и внутренними. А их количество называют «степенью статической неопределимости». Как ее определить?

В балках, а также и в простых рамах, то есть в рамах, не содержащих в своем составе так называемых замкнутых контуров, степень статической неопределимости можно найти по формуле:

n=ΣR—Ш-3,где: ΣR – количество всех возможных опорных реакций (в жесткой заделке реакций может быть три, в шарнирно-неподвижной опоре две, а в шарнирно-подвижной опоре — одна),

Ш – число простых шарниров, то есть таких, которые соединяют лишь два элемента, не больше

Если в узле сходится более двух элементов, то Ш=m-1, где m – количество сходящихся в узле стержней. Например,

m=3, Ш=3-1=2

3 (три) – число уравнений статики.

В сложных рамах применима другая формула:

где К – число замкнутых контуров

В методе сил расчет строится так, что в первую очередь определяются «лишние» неизвестные. Для этого составляют и решают канонические (стандартные) уравнения в количестве, равном степени статической неопределимости.

Здесь обозначено: Х₁, Х₂ – «лишние» неизвестные силы или усилия,

δ₁₁, δ₁₂, δ₂₁, δ₂₂ – главные и побочные коэффициенты,

Все коэффициенты по физическому смыслу являются перемещениями в так называемой основной системе по направлению лишних неизвестных: δ₁₁, δ₁₂, Δ_1F – по направлению Х₁, а δ₂₁, δ₂₂, Δ_2F – по направлению Х₂. Все эти перемещения определяются методом Мора с помощью «перемножения» эпюр изгибающих моментов, построенных в основной системе отдельно от каждой лишней неизвестной силы, равной единице (эп. от Х₁=1; эп. от Х₂=1), а также отдельно от всей заданной нагрузки (эпюра М_F):

После определения значений «лишних» неизвестных окончательную эпюру моментов можно построить по формуле:

📹 Видео

МЕТОД ПОДСТАНОВКИ 😉 СИСТЕМЫ УРАВНЕНИЙ ЧАСТЬ I#математика #егэ #огэ #shorts #профильныйегэСкачать

Уравнение. 5 класс.Скачать

5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Метод выделения полного квадрата. 8 класс.Скачать

Пропорция. Основное свойство пропорции. Практическая часть - решение задачи. 2 часть. 6 класс.Скачать

Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Математика без Ху!ни. Уравнение плоскости.Скачать

Видеоурок "Параметрические уравнения прямой"Скачать

СЛОЖИТЕ ДВА КОРНЯСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Видеоурок "Канонические уравнения прямой"Скачать

Разложение составных чисел на простые множители. 5 класс.Скачать