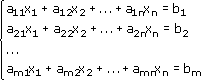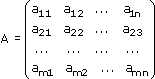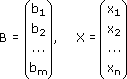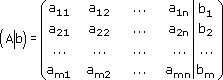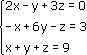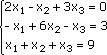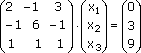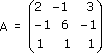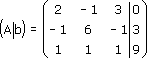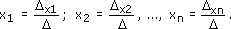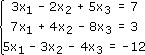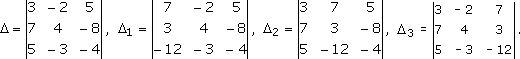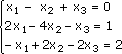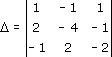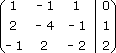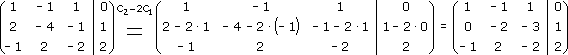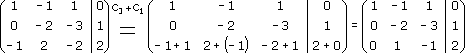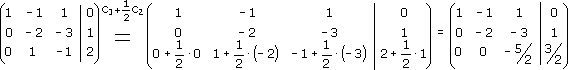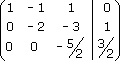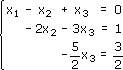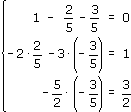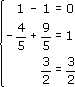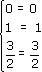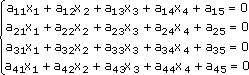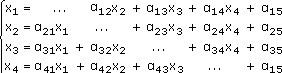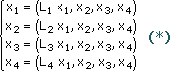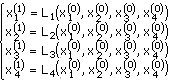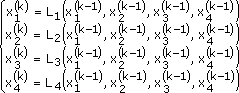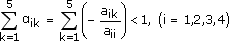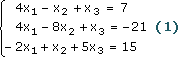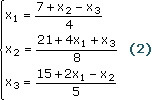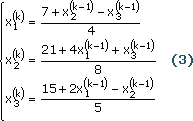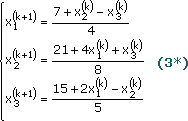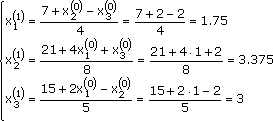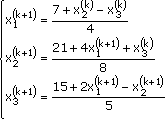Численные методы решения систем линейных уравнений информатика

по информатике на тему:

«Численные методы решения

систем линейных уравнений»

студент 06–ИСТ, Фадеева Т.В.

I Теоретическая часть

2. Численные методы . 6

1) Матричный метод. 6

2) Метод Крамера. 9

3) Метод Гаусса …………. 12

4) Итерации для линейных систем….…..…..17

a) Итерация Якоби..………………. …..18

b) Итерация Гаусса – Зейделя..……. …20

II Практическая часть

1) Матричный метод. 22

2) Метод Крамера. 24

3) Метод Гаусса……. 26

4) Листинг программы.……………………….28

III Польза введения расчётов.……………………………….65

IV Литература………. 66

I. Теоретическая часть.

Линейная алгебра – часть алгебры, изучающая векторные (линейные) пространства и их подпространства, линейные отображения (операторы), линейные, билинейные, и квадратичные функции на векторных пространствах.

Линейная алгебра, численные методы – раздел вычислительной математики, посвященный математическому описанию и исследованию процессов численного решения задач линейной алгебры.

Среди задач линейной алгебры наибольшее значение имеют две: решение системы линейных алгебраических уравнений определение собственных значений и собственных векторов матрицы. Другие часто встречающиеся задачи: обращение матрицы, вычисление определителя и т.д.

Любой численный метод линейной алгебры можно рассматривать как некоторую последовательность выполнения арифметических операций над элементами входных данных. Если при любых входных данных численный метод позволяет найти решение задачи за конечное число арифметических операций, то такой метод называется прямым. В противоположном случае численный метод называется итерационным. Прямые методы — это такие, как метод Гаусса, метод окаймления, метод пополнения, метод сопряжённых градиентов и др. Итерационные методы – это метод простой итерации, метод вращений, метод переменных направлений, метод релаксации и др. Здесь будут рассматриваться матричный метод, метод Гаусса и метод Крамера.

В данной работе будут рассмотрены численные методы в электронных таблицах Excel и программе MathCAD, Microsoft Visual Basic.

Программа MathCAD по своему назначению позволяет моделировать в электронном документе научно–технические, а также экономические расчёты в форме, достаточно близкой к общепринятым ручным расчётам. Это упрощает составление программы расчёта, автоматизирует перерасчёт и построение графических иллюстраций подобно электронным таблицам Excel, документирование результатов как в текстовом редакторе Word.

Программа Mathcad известна за лёгкость, с которой математические уравнения, текст, и графика могут быть объединены в одном документе. Кроме того, вычислительные способности Mathcad распространяются от сложения столбца чисел к решению интегралов и производных, решение систем уравнений и больше.

Достоинством MathCAD является также наличие в его составе электронных книг. Одна из них – учебник по самой программе, другие – справочник по различным разделам математики, физики, радиоэлектроники и др.

Microsoft Office Excel.

Если же говорить о программе Excel, которая является одной из наиболее известных в обработке электронных таблиц, то без преувеличения можно утверждать, что ее возможности практически неисчерпаемы.

Обработка текста, управление базами данных — программа настолько мощна, что во многих случаях превосходит специализированные программы — редакторы или программы баз данных. Такое многообразие функций может поначалу запутать, нежели заставить применять их на практике. Но по мере приобретения опыта начинаешь по достоинству ценить то, что границ возможностей Excel тяжело достичь.

За всю историю табличных расчетов с применением персональных компьютеров требования пользователей к подобным программам существенно изменились. В начале основной акцент в такой программе, как, например, Visi Calc, ставился на счетные функции. Сегодня, положение другое. Наряду с инженерными и бухгалтерскими расчетами организация и графическое изображение данных приобретают все возрастающее значение. Кроме того, многообразие функций, предлагаемое такой расчетной и графической программой, не должно осложнять работу пользователя. Программы для Windows создают для этого идеальные предпосылки.

В последнее время многие как раз перешли на использование Windows в качестве своей пользовательской среды. Как следствие, многие фирмы, создающие программное обеспечение, начали предлагать большое количество программ для Windows.

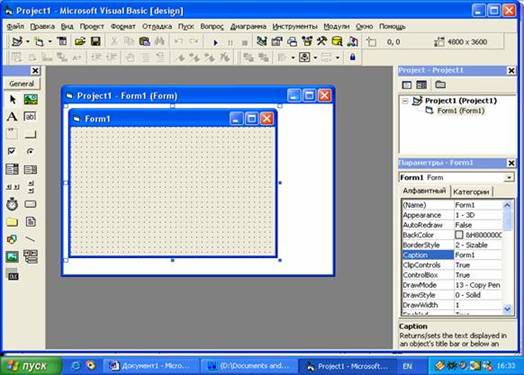
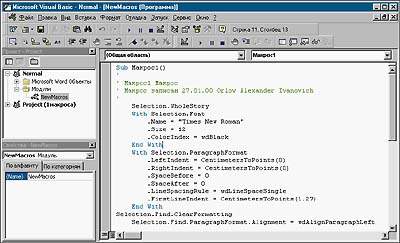
Microsoft Visual Basic – это мощная система программирования, позволяющая быстро и эффективно создавать приложения для Microsoft Windows. В отличие от Excel и MathCAD это наиболее удобная программа для решения систем линейных уравнений. Простой пользовательский интерфейс, позволяющий легко переключаться с проекта формы на сам код программы.

Удобное окно для кода самой программы:

Разрешимость системы линейных уравнений.

Когда мы говорим о главной матрице системы линейных уравнений, то всегда имеем в виду квадратную матрицу n×n, т. е. матрицу с одинаковым количеством строк и столбцов. Это важно.

Если, например, количество строк (количество уравнений в системе) будет меньше, чем количество столбцов (фактически, количества неизвестных), то система будет неопределенной, т. е. мы не сможем однозначно определить все неизвестные (решить систему).

Но это не единственное ограничение. Из векторной алгебры известно, что система линейных уравнений имеет решение (однозначное) тогда и только тогда, когда ее главный определитель не равен нулю: Δ ≠ 0.

Рассмотрим случай, когда определитель системы равен нулю. Здесь возможны два варианта:

1. Δ = 0 и каждый из дополнительных определителей Δx_i = 0. Это имеет место только тогда, когда коэффициенты при неизвестных x_i пропорциональны, т. е. каждое уравнение системы получается из первого уравнения умножением обеих его частей на число k. При этом система имеет бесчисленное множество решений.

2. Δ = 0 и хотя бы один дополнительный определитель Δx_i ≠ 0. Это имеет место только тогда, когда коэффициенты при всех неизвестных x_i, пропорциональны. При этом получается система из противоречивых уравнений, которая не имеет решений.

Матричный метод решения систем линейных уравнений.

Пусть дана система линейных уравнений:

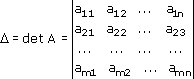
Рассмотрим матрицу, составленную из коэффициентов при неизвестных:

Свободные члены и неизвестные можно записать в виде матрицы столбцов:

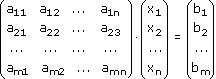
Тогда, используя правило умножение матриц, эту систему уравнений можно записать так:

Равенство (1) называется матричным уравнением или системой уравнений в матричном виде.

Матрица А коэффициентов при неизвестных называется главной матрицей системы.

Иногда рассматривают также расширенную матрицу системы, т. е. главную матрицу системы, дополненную столбцом свободных членов, которую записывают в следующем виде:

Любую линейную систему уравнений можно записать в матричном виде. Например, пусть дана система:

Эта система из двух уравнений с тремя неизвестными – x, y,. В высшей математике можно рассматривать системы из очень большого числа уравнений с большим количеством неизвестных и поэтому неизвестные принято обозначать только буквой х, но с индексами:

Запишем эту систему в матричном виде:

Здесь главная матрица системы:

Расширенная матрица будет иметь вид:

Решения матричных уравнений.

Матричные уравнения решаются при помощи обратных матриц. Уравнение решается следующим образом. Пусть матрица А – невырожденная (D ≠ 0), тогда существует обратная матрица А-1. Умножив на нее обе части матричного уравнения, имеем А-1(АХ) = А-1В. Используя сочетательный закон умножения, перепишем это равенство в виде

Поскольку А-1 А = Е и ЕХ = Х, находим:

Таким образом, чтобы решить матричное уравнение, нужно:

1. Найти обратную матрицу А-1.

2. Найти произведение обратной матрицы А-1 на матрицу столбец свободных членов В, т. е А-1В.

Пользуясь определением равных матриц, записать ответ.

При этом собственно нахождение обратной матрицы – процесс достаточно трудоемкий и его программирование вряд ли можно назвать элементарной задачей. Поэтому на практике чаще применяют численные методы решения систем линейных уравнений.

К численным методам решения систем линейных уравнений относят такие как: метод Гаусса, метод Крамера, итеративные методы. В методе Гаусса, например, работают над расширенной матрицей системы. А в методе Крамера – с определителями системы, образованными по специальному правилу.

При решении систем линейных уравнений по методу Крамера последовательно выполняется следующий алгоритм:

1. Записывают систему в матричном виде (если это еще не сделано).

2. Вычисляют главный определитель системы:

3. Вычисляют все дополнительные определители системы:

4. Если главный определитель системы не равен нулю, то выполняют пункт 5. Иначе рассматривают вопрос о разрешимости данной системы (имеет бесчисленное множество решений или не имеет решений). Находят значения всех неизвестных по формулам Крамера для решения системы n линейных уравнений с n неизвестными, которые имеют вид:

Решить по методу Крамера систему из трех уравнений с тремя неизвестными:

Запишем главный и побочные определители системы:

Вычислим эти определители:

Δ1 = -112+(-45)+(-192)-(-240)-24-168 = -112-45-192+240-24-168 = 240-541 = -301.

Δ2 = -36-420-280-75+196-288 = 196-1099 = -903.

Δ3 = -144-147-30-140+27-168 = -629+27 = -602.

Главный определитель системы не равен нулю. Находим неизвестные по формулам Крамера.

Подставим найденные значения определителей в формулы Крамера:

x1 = Δ1/Δ = -301/(-205) = 1,468292682927 ≈ 1,47;

x2 = Δ2/Δ = -903/(-205) = 4,40487804878 ≈ 4,4;

x3 = Δ3/Δ = -602/(-205) = 2,936585365854 ≈ 2,93.

При решении систем линейных уравнений по методу Крамера используются формулы, в которых участвуют как главный, так и дополнительные определители системы:

Напомним, что главным определителем системы называется определитель главной матрицы системы, составленной из коэффициентов при неизвестных:

Если в главном определителе системы заменить поочередно столбцы коэффициентов при x₁, x₂. x_n на столбец свободных членов, то получим n дополнительных определителей (для каждого из n неизвестных):

При этом важен вопрос о разрешимости данной системы, который решается сравнением главного и дополнительных определителей системы с нулем:

Метод Гаусса – прямой и обратный ход.

Рассмотрим метод Гаусса. Например, пусть дана расширенная матрица некоторой системы m линейных уравнений c n неизвестными:

Будем считать, что a₁₁ ≠ 0 (если это не так, то достаточно переставить первую и некоторую другую строку расширенной матрицы местами). Проведем следующие элементарные преобразования:

Т. е. от каждой строки расширенной матрицы (кроме первой) отнимаем первую строку, умноженную на частное от деления первого элемента этой строки на диагональный элемент а₁₁.

В результате получим матрицу:

Т. е. первая строка осталась без изменений, а в столбце под а₁1 на всех местах оказались нули. Обратим внимание, что преобразования коснулись всех элементов строк, начиная со второй, всей расширенной матрицы системы.

Теперь наша задача состоит в том, чтобы получить нули подо всеми диагональными элементами матрицы А – a_ij, где I = j.

Повторим наши элементарные преобразования, но уже для элемента α₂₂.

Т. е. от каждой строки расширенной матрицы (теперь кроме первой и второй) отнимаем вторую строку, умноженную на частное от деления первого элемента этой (текущей) строки на диагональный элемент α₂₂.

Такие преобразования продолжаются до тех пор, пока матрица не приведется к верхнее — треугольному виду. Т. е. под главной диагональю не окажутся все нули:

Вспомнив, что каждая строка представляет собой одно из уравнений линейной системы уравнений, легко заметить, что последнее m-ое уравнение принимает вид:

Отсюда легко можно найти значение первого корня – x_n = δ_m/γ_mn.

Подставив это значение в предыдущее m-1-е уравнение, легко получим значение x_n-1-ого корня.

Таким образом, поднимаясь до самого верха обратным ходом метода Гаусса, мы последовательно найдем все корни системы уравнений.

Рассмотрим систему уравнений:

Главный определитель данной системы:

Т. е. система определена и разрешима. Решим ее по методу Гаусса.

Проведем прямой ход метода Гаусса, выписав предварительно расширенную матрицу системы:

Получим нули под главной диагональю в первом столбце расширенной матрицы. Для получения нуля в элементе a21 (т. е. под диагональю во второй строке матрицы) вторую строку матрицы преобразуем по формуле C₂-(a₂₁/a₁₁)*C₁ = C₂-(2/1)*C₁ = C₂-2*C₁:

Аналогично поступаем и с элементом а31 (т. е. под диагональю в третьей строке матрицы). Третью строку матрицы преобразуем по формуле C₃-(a₃₁/a₁₁)*C₁ = C₃-(-1/1)*C₁ = C₃+C₁:

Таким образом, мы получили нули под главной диагональю в первом столбце расширенной матрицы. Осталось получить нуль под главной диагональю во втором столбце матрицы, т. е. на месте элемента а32. Для этого третью строку матрицы преобразуем по формуле C₃-(a₃₂/a₂₂)*C₂ = C₃-(1/-2)*C₂ = C₃+1/2C₂:

Таким образом, проведя прямой ход метода Гаусса, мы получили расширенную матрицу системы, приведенную к верхне-треугольному виду:

Эта матрица эквивалентна системе:

Обратным ходом метода Гаусса найдем корни системы. Из последнего уравнения найдем корень х₃:

Корень x₃ = -3/5 найден. Подставим его в верхнее (второе) уравнение системы (-2x₂-3x₃ = 1):

Корень x₂ = 2/5 найден. Подставим его и корень х₃ в верхнее (первое) уравнение системы (x₁-x₂+x₃ = 0):

Итак, метод Гаусса (или, иначе, метод последовательного исключения неизвестных) состоит в следующем:

1. Путем элементарных преобразований систему уравнений приводят к эквивалентной ей системе с верхне-треугольной матрицей. Эти действия называют прямым ходом.

2. Из полученной треугольной системы переменные находят с помощью последовательных подстановок (обратный ход).

3. При этом все преобразования проводятся над так называемой расширенной матрицей системы, которую и приводят к верхнее — треугольному виду в прямом ходе метода.

Итерация для линейных систем.

Способ итераций дает возможность получить последовательность приближенных значений, сходящихся к точному решению системы, подобно тому, как это делается для одного уравнения.

Для определенности ограничимся системой из четырех уравнений с четырьмя неизвестными (система четвертого порядка), которую запишем в виде:

Разрешим первое уравнение системы относительно х₁:

Затем разрешим второе уравнение относительно х₂ и т. д. Тогда систему можно переписать в виде:

где α = -a_ik/a_ii, i = 1, 2, 3, 4; k = 1, 2, 3, 4, 5.

Система является частным случаем записи вида:

При этом линейная функция L₁ фактически не зависит от х₁.

Зададим какие-либо начальные значения неизвестных (нулевые приближения):

Подставляя эти значения в правые части системы (*), получим первые приближения:

Полученные первые приближения могут быть так же использованы для получения вторых, третьих и т. д. приближений. Т. е. можно записать:

Условия сходимости итерационного процесса.

Установим условия, выполнение которых обеспечит сходимость получающихся приближений к истинному (точному) решению системы х₁, х₂, х₃, х₄.

Не вдаваясь в подробности, скажем, что для того чтобы итерационный процесс сходился к точному решению, достаточно, чтобы все коэффициенты системы были малы по сравнению с диагональными.

Это условие можно сформулировать и более точно:

Для сходимости процесса итераций достаточно, чтобы в каждом столбце сумма отношений коэффициентов системы к диагональным элементам, взятым из той же строки, была строго меньше единицы:

Рассмотрим систему линейных уравнений:

Уравнения можно записать в виде:

Это позволяет предложить следующий итерационный процесс:

или (другой вид записи)

Покажем, что если начать с точки P₀ = (х₁ (0) , х₂ (0) , х₃ (0) , х₄ (0) ) = (1, 2, 2), то итерация (3) сходится к решению (2, 4, 3). Подставим х₁ = 1, х₂ = 2, х₂ = 2 в правую часть каждого уравнения из (3), чтобы получить новые значения:

Новая точка P₁ = (х₁ (1) , х₂ (1) , х3 (1) , х₄ (1) ) = (1.75, 3.375, 3), ближе, чем P₀.

Итерация, использующая (3), генерирует последовательность точек <P_k>, которая сходится к решению (2, 4, 3):

k	х1(k)	х2(k)	х3(k)
0	1.0	2.0	2.0
1	1.75	3.375	3.0
2	1.84375	3.875	3.025
3	1.9625	3.925	2.9625
4	1.990625	3.9765625	3.0
5	1.99414063	3.9953125	3.0009375
…	…	…	…
15	1.99999993	3.99999985	3.0009375
…	…	…	…
19	2.0	4.0	3.0

Этот процесс называется итерацией Якоби и может использоваться для решения определенных типов линейных систем.

Процесс итерации Якоби иногда можно модифицировать для ускорения сходимости.

Отметим, что итеративный процесс Якоби производит три последовательности – <х₁ (k) >, <х₂ (k) >, <х₃ (k) >, <х₄ (k) >. Кажется разумным, что х₁ (k+1) может быть использовано вместо х₂ (k ). Аналогично х₁ (k+1) и х₂ (k+1) можно использовать в вычислении х₃ (k+1) . Например, для уравнений из системы (1) это даст следующий вид итерационного процесса Гаусса-Зейделя, использующий (3*):

Такой итерационный процесс даст результаты:

01.02.02.011.753.752.9521.953.968752.9862531.9956253.996093752.99903125…………81.999999833.999999882.9999999691.999999983.999999993.0102.04.03.0

Т. е. к точному решению мы пришли уже на 10-ом шаге итерации, а не на 19, как в итерации Якоби.

1. Способ итераций дает возможность получить последовательность приближенных значений, сходящихся к точному решению системы. Для этого система приводится к виду (для случая системы из четырех уравнений):

Эти формулы как раз и задают собственно итерационный процесс.

Информатика, часть 1. «Численные методы»

Государственный комитет РФ по связи и

Сибирский государственный университет

телекоммуникаций и информатики

Методические указания предназначены для студентов заочного отделения инженерно-технических факультетов, изучающих вычислительную технику и программирование в 3-м семестре. Они содержат необходимый теоретический минимум, задачи для курсовой работы и рекомендуемую литературу.

Кафедра прикладной математики и кибернетики.

Для специальностей 2305, 2306, 2307.

Список литературы – 9 наименований.

Утверждено редакционно-издательским советом СибГУТИ в качестве методических указаний.

© Сибирская государственная академия

телекоммуникаций и информатики, 1999 г.

1. Введение

Для современных инженерно-технических задач необходимо использовать сложный математический аппарат и развитые методы их решения. При этом часто приходится встречаться с задачами, для которых аналитическое решение, т. е. общее решение в виде аналитического выражения, связывающего исходные данные задачи с требуемыми результатами, либо вообще невозможно, либо выражается такими громоздкими формулами, что использование их для практических целей явно нецелесообразно.

В этом случае применяются численные методы решения, которые позволяют достаточно просто получить решение поставленной задачи. Численные методы легко реализуются на ЭВМ с помощью вычислительных алгоритмов.

Все многообразие численных методов подразделяют на две группы — точные и приближенные.

Точными называют методы, позволяющие решить задачу в точной постановке. Точные методы не вносят погрешностей в вычисления.

Бывает так, что решить задачу в точной постановке трудно или даже невозможно. Тогда ее заменяют близкой по результатам приближенной задачей. Численный метод, реализующий такую приближенную задачу, называют приближенным методом. Приближенные методы вносят погрешности в вычисления.

Численные методы реализуются конечными или бесконечными вычислительными алгоритмами.

Приближенные методы, основанные на последовательном приближении к решению путем многократного применения какой-либо вычислительной процедуры, называют итерационными методами. В итерационных методах исходными данными для каждой последующей вычислительной процедуры являются результаты применения предыдущих процедур. Итерационные методы позволяют получить приближенное решение, сколь угодно мало отличающееся от точного решения.

Настоящие методические указания содержат основы курса «Численные методы». Для более детального изучения данного курса следует воспользоваться рекомендуемой литературой. Кроме того, для выполнения курсовой работы необходимо использовать знания, полученные в предыдущем семестре в процессе изучения курса «Вычислительная техника и программирование».

2. Абсолютная и относительная погрешность

Определения

Определение. Абсолютной погрешностью величины x называется величина

где x – приближенное значение, x0 – точное значение.

Следствие этой формулы:

Пример. Результат измерений длины комнаты – 10,2 ± 0,01 м.

Здесь, 10,2 м – приблизительное значение – результат измерений, 0,01 – погрешность измерений – абсолютная погрешность.

Обычно должно быть D x ú -1 ï + ú 2 ï; ï -5 ï > ú -2 ï + ú 1 ï; ï 4 ï > 1 + ú -2 ï.

После этого приводим систему к виду, удобному для итераций.

Получаем: , находим

.

Аналогично находятся последующие приближения X(3), X(4) и т. д.

Сравнив и , можно заметить, что они отличаются друг от друга очень незначительно (в третьем знаке после запятой) и, следовательно, в качестве решения с точностью e =10-2 можно взять X(10) . Для сведения: точное решение этой СЛУ – .

4. Решение нелинейных уравнений

Если непрерывная функция f(x) принимает значения различных знаков на концах отрезка [a, b], то есть f(a)×f(b)

Использование табличного процессора MS Excel для численного решения систем линейных уравнений и вычисления определенного интеграла
учебно-методическое пособие на тему

Учебно-методическое пособие Использование табличного процессора MS Excel для численного решения систем линейных уравнений и вычисления определенного интеграла разработано для организации самостоятельной работы студентов и соответствует действующей программе по курсу дисциплины «Информатика и ИКТ» для темы «Возможности динамических (электронных) таблиц. Математическая обработка числовых данных» раздела «Технология создания и преобразования информационных объектов».

Кротко изложены основы технологии работы с табличным процессором MS Excel и основы численных методов решения математических задач для систем линейных уравнений и вычисления определенного интеграла. Приведена пошаговая реализация нахождения неизвестных для системы линейных уравнений и вычисления значения определенного интеграла на конкретных примерах с использованием MS Excel. Представлены индивидуальные задания для самостоятельной работы студентов.

Учебное пособие предназначено для студентов образовательных учреждений среднего профессионального образования, изучающих дисциплину «Информатика и ИКТ», а также для реализации математических моделей с помощью компьютера при выполнении расчетно-графических, курсовых и дипломных работ.

Скачать:

Вложение	Размер
chisl.metody_v_excel.doc	698 КБ

Предварительный просмотр:

МИНИСТЕРСТВО ОБРАЗОВАНИЯ НИЖЕГОРОДСКОЙ ОБЛАСТИ

Государственное бюджетное профессиональное образовательное учреждение «Кстовский нефтяной техникум имени Бориса Ивановича Корнилова»

Система качества образовательного учреждения

Использование табличного процессора MS Excel для численного решения систем линейных уравнений и вычисления определенного интеграла

Учебно-методическое пособие
для самостоятельной работы студентов
по дисциплине « Информатика и ИКТ »

Учебно-методическое пособие Использование табличного процессора MS Excel для численного решения систем линейных уравнений и вычисления определенного интеграла разработано для организации самостоятельной работы студентов и соответствует действующей программе по курсу дисциплины «Информатика и ИКТ» для темы «Возможности динамических (электронных) таблиц. Математическая обработка числовых данных» раздела « Технология создания и преобразования информационных объектов».

Кротко изложены основы технологии работы с табличным процессором MS Excel и основы численных методов решения математических задач для систем линейных уравнений и вычисления определенного интеграла. Приведена пошаговая реализация нахождения неизвестных для системы линейных уравнений и вычисления значения определенного интеграла на конкретных примерах с использованием MS Excel. Представлены индивидуальные задания для самостоятельной работы студентов.

Учебное пособие предназначено для студентов ГБОУ СПО «Кстовский нефтяной техникум им. Б.И. Корнилова», изучающих дисциплину «Информатика и ИКТ», а также для реализации математических моделей с помощью компьютера при выполнении расчетно-графических, курсовых и дипломных работ.

1.5. Основные правила создания формул и функций

Учебно-методическое пособие для самостоятельной работы студентов разработано в соответствии с действующей программой по курсу дисциплины «Информатика и ИКТ» для темы «Возможности динамических (электронных) таблиц. Математическая обработка числовых данных» раздела « Технология создания и преобразования информационных объектов».

Учебно-методическое пособие содержит теоретический материал по технологии использования табличного процессора MS Excel и математическим методам решения систем линейных уравнений и приближенному вычислению определенного интеграла, который является основой для практического использования решения математических задач с помощью компьютерных технологий. В разделе «Реализация решения математических задач в MS Excel» приведены подробные пошаговые решения примеров решения системы линейных уравнений и приближенного вычисления интеграла, которые могут быть воспроизведены студентом самостоятельно. Для закрепления полученных навыков в соответствии предлагаемыми методическими указаниями студент должен выполнить индивидуальные задания и представить их на проверку преподавателю.

Содержание учебно-методического пособия отражает практическую направленность использования компьютера для решения профессиональных задач, так как большинство инженерных задач использующих математические методы требуют сложных длительных вычислений, которые существенно упрощаются и сокращаются при использовании компьютерных технологий. Полученные студентом знания и умения, в первую очередь, могут быть использованы при выполнении расчетно-графических, курсовых работ и. конечно, при выполнении дипломной работы.

1. Табличный процессор Excel и технология работы в нем

1.1. Структура документа MS Excel

MS Excel – это прикладная программа управления электронными таблицами, которая используется для выполнения вычислений, организации данных, анализа результатов и поиска оптимальных решений.

Базовыми понятиями в Excel являются: книга, лист, таблица, ячейка .

Структуру книги можно представить следующим образом (см. Рис.1).

Книга в Excel представляет собой файл с расширением xls . Имя книги (файла) задается при ее сохранении и должно напоминать о ее содержании. Каждая книга может состоять из нескольких поименованных листов (до 255, а по умолчанию – 3). Имя листа указано на ярлычке (внизу листа) и может быть изменено, чтобы напоминать о его содержании. Для перехода на другой лист надо щелкнуть ЛКМ (ЩЛКМ) по его ярлычку. Листы можно добавлять, удалять, копировать или переименовывать (ЩПКМ – щелчок правой кнопкой мыши по ярлычку и появится контекстное меню). Лист – это место для ввода, хранения и обработки данных. Лист Excel состоит из ячеек , каждая из которых имеет свой адрес . Ячейки образуют строки (до 65536) и столбцы (до 256). Строки имеют номера, а столбцы по умолчанию – буквенные имена (если стиль ссылок А1 ), или номера, если установлен стиль ссылок R1C1 (R – строка, а С – столбец). Стили ссылок задаются параметрами при работе с опциями меню «Сервис». Как правило, используется стиль А1.

1.2. Основной принцип работы электронных таблиц

Каждая ячейка листа может содержать текст, числовое значение или формулу и быть отформатирована.

Основной принцип работы электронных таблиц заключается в том, что одни ячейки рабочего листа используются как независимые переменные (влияющие ячейки), которым задаются значения из вне (например, пользователем), а другие ячейки используются как зависимые переменные (зависимые ячейки), которые содержат формулы, ссылающиеся на независимые переменные. Пользователь вводит исходные данные (текст или числа) во влияющие ячейки и формулы в зависимые ячейки, далее автоматически (или, в зависимости от настройки, по команде) производятся вычисления по формулам, и пользователь видит готовый результат в зависимых ячейках. Если же установить режим показа формул («Сервис Параметры»), то в зависимых ячейках будут видны только формулы.

Если же режим показа формул не установлен , то в ячейке Е2 сразу появится результат (=4,5).

На листе может быть создана одна или несколько таблиц.

Таблица – это совокупность ячеек, связанных между собой по смыслу или с помощью формул в соответствии с задачей пользователя.

Ячейки таблиц, размещенных на разных листах книги или в разных книгах, также могут быть взаимосвязаны посредством формул. На основе таблицы (для наглядности при анализе исходных данных и результатов вычислений) может создаваться диаграмма , которую можно разместить на листе вместе с таблицей или на отдельном листе.

1.3. Ввод информации в ячейки

Как правило, построение таблицы начинается с заполнения заголовков столбцов (а, если необходимо, и строк, как на Рис.1), поясняющих содержание основных ячеек таблицы, в которых находятся исходные данные и формулы. Перед вводом информации в ячейку ее надо выделить с помощью ЩЛКМ по ячейке или с помощью клавиш перемещения курсора.

Существуют следующие основные способы ввода информации в ячейки:

1) Неавтоматизированный способ, при котором каждый символ вводится с клавиатуры. Он занимает много времени и имеет большую вероятность ошибок, но необходим тогда, когда в таблице нет повторяющейся, либо закономерно изменяющейся информации, что бывает очень редко.

Ввод информации должен быть зафиксирован. Это достигается либо нажатием клавиши ENTER или нажатием клавиш управления курсором на клавиатуре (стрелки ↑ , ← , ↓ , → ). Для изменения (редактирования) информации в ячейке надо сначала 2 раза ЩЛКМ по ней. Например, на Рис. 1 в ячейках А2 и D4 записана информация, изменяющейся не закономерно, поэтому ее невозможно вводить иначе, чем в ручную с клавиатуры.

Полезно запомнить, что:

– при вводе в ячейку длинного предложения для перехода на новую строку (в той же ячейке) надо нажать ALT+ENTER .

– если при вводе обнаружена ошибка, то следует нажать на панели инструментов (ПИ) кнопку ОТМЕНИТЬ .

2) Автоматизированный способ , который может быть реализован двумя методами:

• копирования в буфер ранее заполненной ячейки (или группы ячеек), которые предварительно должны быть выделены, и последующей вставки из буфера в нужную область таблицы, предварительно выделив левую верхнюю ячейку этой области. Для выделения группы смежных ячеек надо выделить первую ячейку диапазона, затем нажать и удерживая SHIFT выделить последнюю ячейку диапазона.
• автозаполнение рядов . Ряд – это группа смежных ячеек, принадлежащая одному столбцу или строке и содержащая одинаковую или закономерно изменяющуюся информацию .

Перед автозаполнением надо записать в начальную ячейку текст, число, дату, формулу и т.п., затем выделить эту ячейку и установить указатель мыши над маркером заполнения (маленького черного квадрата в правом нижнем углу выделенной ячейки). При этом вид указателя мыши меняется на знак + , означающий, что автозаполнение разрешено. Затем, нажав ЛКМ, перетащить указатель по ячейкам, которые нужно заполнить информацией и отпустить ЛКМ. При перемещении указателя вниз или вправо, автозаполнение создает в отмечаемых ячейках возрастающие значения, при перемещении указателя вверх или влево отмечаемые ячейки заполняются убывающими значениями.

Если в первоначально выделенной ячейке не распознается закономерность для возрастания или убывания, то ячейки просто дублируются.

Так, например, если в первой ячейке была запись «Блок1», то при перемещении указателя вниз, в последующих ячейках автоматически появятся записи «Блок2», «Блок3» и т.д. В то же время, если в первой ячейке было записано слово «Блок», то в последующих ячейках это слово просто дублируется.

В нашем примере, ячейку Е3 (Рис. 1) целесообразно заполнять с помощью метода автозаполнение рядов, т.е. не вводить в нее формулу, а распространив автозаполнением в нее содержимое ячейки Е2 . При этом содержимое формулы Е3 (аргументы функции СРЗНАЧ()) будут отличаться от аргументов этой же функции для ячейки Е2 по условию автозаполнения:

для Е2: =СРЗНАЧ(С2:D2);

для Е3: =СРЗНАЧ(С3:D3).

Существует и другая возможность автозаполнения рядов – через главное меню: для копирования одной ячейки в несколько смежных или для настройки закономерности автозаполнения можно воспользоваться командой «ПРАВКА ЗАПОЛНИТЬ …».

1.4. Форматирование таблиц

Форматирование в MS Excel осуществляется почти так же, как и в других приложениях MS Office.

Для облегчения визуального поиска в таблице требуемой информации целесообразно заголовки столбцов и строк таблицы выделять цветом, отличительным (от другого текста) шрифтом, заливкой, граничной линией и т.п. В некоторых случаях, для более полного восприятия заголовка, целесообразно объединять ячейки.

Для выполнения вышеуказанных действий используется операция форматирования .

Объектом форматирования могут быть отдельные ячейки или группа ячеек (диапазон), которые предварительно должны быть выделены. ЩПКМ по выделенному объекту приводит к вызову контекстного меню, в котором следует выбрать пункт « формат ячеек» .

Для изменения ширины столбцов или высоты строк таблицы надо поместить указатель мыши (УМ) между соответствующими именами столбцов или номерами строк листа и, удерживая ЛКМ, передвинуть УМ на нужное расстояние.

Если новая таблица содержит компоненты уже существующей таблицы, то целесообразно скопировать созданную таблицу в другую область листа или на другой лист (книгу) и отредактировать ее под условия создаваемой новой таблицы: удалить (или добавить) столбцы, строки или некоторые ячейки. Для работы с этими объектами их надо выделить.

Чтобы выделить целиком строку надо ЩЛКМ по ее номеру, а для столбца – по его имени. После этого ЩПКМ по выделенному объекту вызвать контекстное меню, из которого затеем выбрать, в соответствие с операцией, пункты « Удалить» или « Добавить ячейки». (Для вставки строки надо выделить строку ниже, а для столбца – выделить столбец правее вставляемого).

1.5. Основные правила создания формул и функций

Каждая формула начинается со знака равенства « =» . Знак равенства указывает процессору MS Excel на то, что следующий за ним текст является формулой. В формулах могут присутствовать арифметические операторы для выполнения действий над константами или числами, которые могут вводиться непосредственно с клавиатуры, либо содержаться в других ячейках. В последнем случае в формуле указываются адреса этих ячеек, т.е. ссылки на них. Если в формуле присутствуют несколько арифметических операторов, то в нее можно включить скобки для определения порядка вычислений. В формулах применяют стандартные арифметические операции и соответствующие операторы: сложение (+), вычитание (-), умножение (*), деление (/), возведение в степень (^), (последовательность выполнения операций такая же, как и в арифметике). Также в формулах могут применяться функции из набора встроенных в Excel функций. Большое количество функций (около 500) в значительной степени определяет область использования Excel. Из набора этих функций , которые сгруппированы по категориям , мы будем использовать следующие: Математические, Статистические, Ссылки и массивы, Логические . В логических функциях для обозначения операций сравнения двух чисел используются операции и соответствующие операторы сравнения: равно (=), больше (>), меньше ( больше или равно (>=), меньше или равно ( не равно (), логическое сложение «ИЛИ» (+), логическое умножение «И» (*). Результатом выполнения операции сравнения является логическое значение ИСТИНА или ЛОЖЬ.

Формула является основным средством для анализа данных . С помощью формул можно складывать, умножать и сравнивать данные, осуществлять их поиск и т.п. Формулы могут ссылаться на ячейки текущего листа, листов той же книги или других книг.

В следующем примере « =(В4+25)/СУММ(D5:F5)» складывается значение ячейки B4 с константой 25. Полученный результат делится на сумму значений в диапазоне ячеек D5:F5 , т.е. на результат операции D5+E5+F5.

В данном примере выражение « СУММ(…)» является функцией , т.е. стандартной формулой.

При решении конкретной задачи для создания функции целесообразно использовать так называемый Мастер функций и действовать в следующем порядке:

1. Выделить ячейку, в которую будет вставляться функция.
2. Запустить МАСТЕР ФУНКЦИЙ (на панели инструментов значок , либо «ГЛАВНОЕ МЕНЮ/ВСТАВКА/ФУНКЦИЯ»).
3. Задать в нужную категорию функции (это определяется интуицией или методом перебора).
4. выделить требуемую функцию, прочитать пояснения внизу окна.
5. Если все понятно, то нажать — «ОК».
6. На появившейся панели формул, ввести требуемую информацию в соответствующие окна аргументов.

Ввод информации в окна, как правило, осуществляется так:

• установить курсор в окно (в первое окно он устанавливается автоматически);
• выделить нужные ячейки мышью, установить курсор в другое окно и т.д.

Если нужные ячейки не видны, то надо свернуть панель формул, нажав на красную кнопку в правой части окна ввода, затем выделить ячейки и развернуть панель формул, снова нажав на красную кнопку в правой части окна. Если же пояснений в этом окне недостаточно, то следует закрыть окно МАСТЕРА ФУНКЦИЙ и использовать справочную систему, для чего надо:

1. ЩЛКМ по знаку вопроса в Горизонтальном меню и выполнить команду: «ВЫЗОВ СПРАВКИ / ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ / (ввести фразу « функции») / ОБЗОР / (нажать кнопку « Вывести») / ( выбрать нужную категорию (раздел), например, « Статистические функции ») / (нажать кнопку « Вывести») / ( выбрать нужную функцию, например, « СРЗНАЧ ») / (прочитать подробное ее описание и рассмотреть примеры ). Выписать наиболее общий пример в тетрадь, закрыть справочную систему.
2. По аналогии с примером, используя МАСТЕР ФУНКЦИЙ, создать нужную функцию и, изменяя исходные данные, проверить ее корректность.

В Excel можно создавать так называемые вложенные функции , т.е. функции, аргументами которых являются другие функции. Возможно до 7 уровней вложения. В этом случае для вставки аргумента-функции, после того как будет открыта панель исходной функции, надо открыть левое окно строки формул (щелкнув по «стрелке вниз» ), выбрать нужную функцию и далее действовать, как и с обычной функцией.

Как правило, формулы используются для определения их значений в зависимости от параметров (исходных данных), т.е. констант и переменных. Однако в Excel есть возможность решать и обратные задачи (« какой должна быть переменная, чтобы формула приняла заданное значение?» ), т.е. определять значение переменной, причем только одной, если задать значение результата вычисления формулы. Для этого надо выделить ячейку для искомой переменной и задать ей ориентировочное значение, а затем выполнить команду «СЕРВИС / ПОДБОР ПАРАМЕТРА» и, в появившемся окне, указать запрашиваемые данные.

В формулах для обращения к ячейкам, в зависимости от решаемой задачи, применяются различные способы и методы ссылок на ячейки.

1.6. Способы и методы формирования в формулах ссылок на ячейки

Ссылкой однозначно определяется ячейка или группа (диапазон) ячеек листа, используемых в формуле . С помощью ссылок можно использовать в формуле данные, находящиеся в различных местах листа, а также использовать значение одной и той же ячейки в нескольких формулах. Кроме того, можно ссылаться на ячейки, находящиеся на других листах книги или в другой книге, или на данные другого приложения.

Ссылки на ячейки других книг называются внешними ссылками. Ссылки на данные других приложений называются удаленными ссылками.

В Excel можно выделить три способа формирования ссылок: координатный относительно листа книги, координатный относительно таблицы и именной .

При координатном способе адрес ячейки определяется местом пересечения столбца и строки листа книги или таблицы.

При именном способе адрес ячейки определяется текстовым именем ячейки (или диапазона ячеек), которое напоминает о содержании ячеек.

1. Координатный способ формирования ссылок относительно листа книги

До настоящего момента мы уже использовали именно такой способ, но к вышесказанному необходимо добавить следующее:

• Чтобы создать ссылку на диапазон ячеек, надо активизировать ячейку левого верхнего угла диапазона, поставить двоеточие ( : ), а затем — активизировать ячейку правого нижнего угла диапазона. Например, в формуле =СУММ(A1:В2) определяется сумма чисел, записанных в четырех ячейках: А1, А2, В1, В2 .
• В формулах Excel используется два метода ссылок на ячейки:

1. относительные ссылки , которые ссылаются на ячейки относительно позиции формулы (т.е. если формулу с относительными ссылками скопировать, например, через буфер, в другую ячейку, то ссылки в ней изменятся на количество строк и столбцов относительно ее исходного расположения);
2. абсолютные ссылки , которые всегда ссылаются на одни и те же ячейки независимо от изменения места расположения формулы после копирования. Для задания абсолютной ссылки в формуле надо перед именем столбца и номером строки ячейки добавить знак $ . Пример: $А$2 (если в формуле указана ссылка А2 – то это относительная ссылка).

1. Координатный способ формирования ссылок относительно таблицы

Для ссылок в формулах на ячейки можно использовать заголовки столбцов и строк таблицы, что делает формулу более наглядной.

Например, если в столбце с заголовком « Физика » содержатся средние баллы экзаменационных оценок по физике полученных соответствующим курсом, а заголовками строк являются « Курс11 », « Курс21 », « Курс31 », то, создав формулу « =Физика Курс31 » в любом месте листа, можно определить средний балл по физике полученный курсом №31. Пробел между заголовками является оператором пересечения диапазонов, который предписывает формуле вернуть значения из ячейки, находящейся в пересечении строки « Курс31 » и столбца « Физика ».

1. Именной способ формирования ссылок

Использование имен может упростить понимание формулы. Например, формула «= X*SIN(X) » более привычна, чем «= А1*SIN(A1) » или формула «= МАКС(Возраст) » проще для понимания, чем формула « =МАКС(C20:C30) ». В этом примере имя «Возраст» представляет группу ячеек «C20:C30». Имена можно использовать на любом листе книги.

Чтобы присвоить имя ячейке или группе ячеек нужно:

1. Выделить ячейку или диапазон ячеек, которому необходимо присвоить имя.

2. Щелкнуть ЛКМ по окну имени, которое находится слева в строке формул (это строка, расположенная над заголовками столбцов).

3. Ввести имя ячейки.

4. Нажать клавишу ENTER.

• выделить диапазон ячеек;
• выполнить команду «ВТАВКА / ИМЯ / ПРИСВОИТЬ». Появится окно, в котором можно присвоить, изменить или удалить имя.

По умолчанию имена являются абсолютными ссылками.

2. Математическая постановка задач

2.1. Метод Крамера решения систем линейных уравнений

Рассмотрим метод Крамера решения систем линейных уравнений для системы из трех уравнений с тремя неизвестными x 1 , x 2 и x 3 , которая имеет вид:

Необходимо найти значение главного определителя, составленного из коэффициентов при неизвестных, т.е. , а также еще трех определителей, получаемых из главного путем замены первого, второго и третьего столбца на столбец свободных членов в исходной системе уравнений, т.е. , и .

Тогда исходная система будет равносильна системе вида:

Если все четыре определителя отличны от нуля, то система имеет единственное решение. Значение неизвестных определяются в виде:

Метод Крамера может быть использован для решения систем линейных уравнений, состоящих из четырех и более уравнений, содержащих, соответственно, четыре и более неизвестных. Однако, для вычисления определителей четвертого и выше порядков следует использовать специальные приемы, которые требуют значительных временных затрат и особого внимания при выполнении вычислений. Выполнение вычислений с помощью MS Excel существенного упрощает решение подобных задач.

2.2. Приближенные методы вычисления определенного интеграла

Значение определенного интеграла численно равно площади так называемой криволинейной трапеции, ограниченной кривой, определяемой подынтегральной функцией y = f ( x ), прямыми x = a , x = b и осью Ox .

Приближенные методы вычисления определенного интеграла сводятся к замене площади вышеуказанной криволинейной трапеции ступенчатой фигуры, состоящей из прямоугольников или прямолинейных трапеций.

Площадь криволинейной трапеции разбивают на n прямоугольников, высоты которых равны y 0 , y 1 , y 2 , . y n -1 и основания .

Если суммировать площади прямоугольников, которые покрывают площадь криволинейной трапеции с недостатком, то значение определенного интеграла может быть вычислено по формуле: .

Если суммировать площади прямоугольников, которые покрывают площадь криволинейной трапеции с избытком (рис. 10.6, б ), то значение определенного интеграла может быть вычислено по формуле: .

Значения y 0 , . y n находят из равенства y k = f ( a + k Δx), k =0, 1, …, n . Эти формулы называются формулами прямоугольников и дают приближенный результат. С увеличением n результат становится более точным.

Геометрический смысл следующего способа приближенного вычисления интеграла состоит в том, что нахождение площади криволинейной трапеции заменяется нахождением площади приблизительно равновеликой «прямоугольной» трапеции.

Пусть необходимо вычислить площадь A 1 AmBB 1 криволинейной трапеции, выражаемую формулой .

Заменим дугу AmB хордой АВ и вместо площади криволинейной трапеции A 1 AmBB 1 вычислим площадь трапеции A 1 ABB 1 : , где АА 1 и ВВ 1 – основание трапеции, а А 1 В 1 – ее высота.

Обозначим f ( a )= A 1 A , f ( b )= B 1 B . Высота трапеции A 1 B 1 = b — a , площадь . Следовательно, или . Это так называемая малая формула трапеций .

Для получения более точного результата необходимо разбить площадь криволинейной трапеции на n площадей ординатами, отстоящими друг от друга на расстоянии Δ x . Суммируем площади получившихся трапеций: S = S 1 + S 2 + S 3 + . + S n , где по малой формуле трапеций ; ; ; . .

Сложив, получим или .

Так как и , то можно записать так называемую большую формулу трапеций: , где y 0 , y 1 , y 2 , . y n – значения подынтегральной функции при значениях аргумента, соответственно, a ; a +Δ x ; a +2Δ x ; a+( n -1)Δ x ; b .

3. Реализация решения математических задач в MS Excel

3.1. Решение систем линейных уравнений с использованием табличного процессора MS Excel

В качестве примера рассмотрим систему уравнений:

1. Оформить заголовок в строке 1 на листе 1 «Решение системы линейных уравнений».
2. В области B3:F6 ввести исходные данные, как показано на рисунке 2.
3. Ввести в ячейку A8 текст заголовка «Метод Крамера».
4. В ячейку A11 ввести текст «Δ=» (выравнивание по правому краю).
5. Скопировать исходные данные C4:E6 в область В10:D12. Это главный определитель системы.
6. Скопировать содержимое ячейки A11 в ячейку F11 .
7. В ячейку G11 ввести формулу « =МОПРЕД(B10:D12) ». Получаем значение главного определителя системы.
8. Скопировать исходные данные C4:E6 в область В14:D16. Скопировать исходные данные F4:F6 в область В14:B16. Это определитель для первого неизвестного x 1.
9. В ячейку A15 ввести текст «Δ x 1=» (выравнивание по правому краю).
10. Скопировать содержимое ячейки A15 в ячейку F15 .
11. В ячейку G15 ввести формулу « =МОПРЕД(B14:D16) ». Получаем значение определителя для первого неизвестного x 1.
12. Скопировать исходные данные C4:E6 в область В18:D20. Скопировать исходные данные F4:F6 в область C18:C20. Это определитель для второго неизвестного x 2.
13. В ячейку A19 ввести текст «Δ x 2=» (выравнивание по правому краю).
14. Скопировать содержимое ячейки A19 в ячейку F19 .
15. В ячейку G19 ввести формулу « =МОПРЕД(B18:D20) ». Получаем значение определителя для второго неизвестного x 2.
16. Скопировать исходные данные C4:E6 в область В22:D24. Скопировать исходные данные F4:F6 в область D22:D24. Это определитель для третьего неизвестного x 3.
17. В ячейку A23 ввести текст «Δ x 3=» (выравнивание по правому краю).
18. Скопировать содержимое ячейки A23 в ячейку F23 .
19. В ячейку G23 ввести формулу « =МОПРЕД(B22:D24) ». Получаем значение определителя для третьего неизвестного x 3.
20. В ячейки H15 , H19 и H23 ввести соответственно текст « x 1=», « x 2=» и « x 2=» (выравнивание по правому краю).
21. В ячейку I15 ввести формулу « =G15/$G$11 » (выравнивание по левому краю). Получаем значение первого неизвестного x 1.
22. Скопировать содержимое ячейки I15 в ячейку I19 . Получаем значение второго неизвестного x 2.
23. Скопировать содержимое ячейки I15 в ячейку I23 . Получаем значение третьего неизвестного x 3.

3.2. Нахождение значений определенного интеграла с использованием табличного процессора MS Excel

В качестве примера рассмотрим нахождение значения определенного интеграла при числе разбиения интервала интегрирования n =10. Следует отметить, что точное значение данного интеграла может быть получено аналитическим методом (метод замены переменной) и оно равно 2.

1. Оформить заголовок в строке 1 на листе 2 «Нахождение значения определенного интеграла».
2. В ячейку A3 с помощью редактора формул вставим вид вычисляемого интеграла как показано на рисунке 3.
3. В ячейки E3 , E4 , E5 и E6 соответственно введем текст: «нижний предел интегрирования», «верхний предел интегрирования», «число разбиений отрезка интегрирования» и «шаг интегрирования».
4. В ячейки D3 , D4 , D5 введем исходные данные, определяющие пределы интегрирования и число разбиений отрезка интегрирования (в нашем примере это числа: 0, 5, 10) (выравнивание по центру).
5. В ячейку D6 введем формулу для определения шага интегрирования « =(D4-D3)/D5 » (выравнивание по центру).
6. Оформим заголовок таблицы для численного вычисления подынтегральной функции в узлах интегрирования: в ячейку A8 вводим текст «x», в ячейку B8 вводим текст «f(x)» (выравнивание по центру).
7. В ячейку A9 вводим формулу « =D3 ».
8. В ячейку A10 вводим формулу « =A9+$D$6 ».
9. Копируем формулу из ячейки A10 в диапазон A11:A19 (используем прием растягивания). Получаем значения узлов интегрирования.
10. В ячейку B9 вводим формулу, определяющую значение подынтегральной функции в первом узле интегрирования. В нашем примере она будет: «=1/КОРЕНЬ(A9+4)».
11. Копируем формулу из ячейки B9 в диапазон B10:B19 (используем прием растягивания). Получаем значения подынтегральной функции в узлах интегрирования.
12. В ячейку D8 введем текст « Приближенное значение интеграла: ».
13. В ячейку D10 введем текст «по формуле прямоугольников:».
14. В ячейку G10 введем формулу « =СУММ(B9:B18)*D6 », которая позволяет вычислить значение определенного интеграла по формуле прямоугольников. Получаем приближенное значение вычисляемого определенного интеграла.
15. В ячейку D12 введем текст «по формуле трапеций:».
16. В ячейку G12 введем формулу « =(2*СУММ(B10:B18)+B9+B19)*D6/2 », которая позволяет вычислить значение определенного интеграла по формуле трапеций. Получаем второе приближенное значение вычисляемого определенного интеграла.

Замечание: оба приближенных значения определенного интеграла близки к его точному значению.

1. В диапазоне A21:H36 с помощью Мастера диаграмм построить график подынтегральной функции на основе диаграммы точечного вида:

1. Выделить диапазон A8:B19;
2. Меню Вставка ⇨ Команда Диаграмма …;
3. На 1-ом шаге выбрать тип диаграммы: Точечная диаграмма со значениями, соединенными сглаживающими линиями и нажать кнопку « Далее »;
4. На 2-ом шаге ничего не изменяем и нажимаем кнопку « Далее »;
5. На 3-ем шаге на вкладке «Заголовки» в окно «Ось Х (категорий) заносим текст «x», а на вкладке «Легенда» снимаем флажок в позиции «Добавить легенду» и нажимаем кнопку « Далее »;
6. На 4-ом шаге нажимаем кнопку « Готово ».

1. Переносим построенную диаграмму в диапазон A21:H36 , сжимая (растягивая) до заданных размеров. Форматируем Ось категорий и Ось значений, переносим подписи осей, форматируем Область построения диаграммы (см. Рис. 3).

4. Методические указания по выполнению самостоятельной работы

1. Повторить материал по теме «Возможности динамических (электронных) таблиц. Математическая обработка числовых данных», прочитав раздел учебно-методического пособия «Табличный процессор Excel и технология работы в нем».
2. Повторить материал по дисциплине «Математика» по решению систем линейных уравнений методом Крамера и приближенному вычислению определенных интегралов, прочитав раздел учебно-методического пособия «Математическая постановка задач».
3. Решить на компьютере с использованием табличного процессора MS Excel систему линейных уравнений из раздела «Реализация решения математических задач в MS Excel».
4. Вычислить на компьютере с использованием табличного процессора MS Excel значение определенного интеграла из раздела «Реализация решения математических задач в MS Excel».
5. Решить на компьютере с использованием табличного процессора MS Excel систему линейных уравнений , применив метод Крамера. Коэффициенты при неизвестных и свободные члены задаются по вариантам, указанным в разделе «Варианты заданий для самостоятельной работы». Результаты решения предоставить преподавателю в виде аналогичном Рис 2.
6. Вычислить на компьютере с использованием табличного процессора MS Excel значение определенного интеграла , применив формулу прямоугольников и формулу трапеций. Построить график подынтегральной функции. Вид подынтегральной функции f ( x ), нижний предел интегрирования a , верхний предел интегрирования b задаются по вариантам, указанным в разделе «Варианты заданий для самостоятельной работы». Число разбиений отрезка интегрирования n равно 10 для всех вариантов. Результаты работы предоставить преподавателю в виде аналогичном Рис 3.

5. Варианты заданий для самостоятельной работы

5.1. Варианты заданий систем линейных уравнений

5.2. Варианты заданий определенного интеграла

🎥 Видео