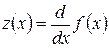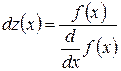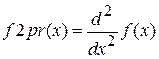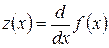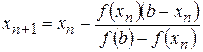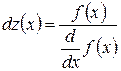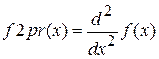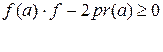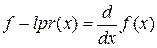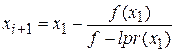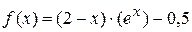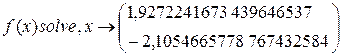Численные методы решение скалярных уравнений

Цель работы:сформировать у студентов представление о применении уравнений в различных областях деятельности, привить знания об основных этапах решения уравнения, выработать навыки использования различных методов для уточнения корня уравнения и выбора того или иного программного средства для проверки правильности найденного результата.

Метод хорд

Решить уравнение е х ∙ (2 – х) – 0,5 = 0 методом хорд с точностью ɛ = 0,001.

1. Отделяем корни.Этот этап решения осуществляется с помощью аналитического или графического метода. После того как корень, подлежащий уточнению, отделен, за начальное приближение может быть выбрана любая точка [a,b] (начало отрезка, его середина и т.д.).

Воспользуемся графическим методом. Построим график функций и найдем точки пересечения его с осью Ох (рис.2.1.).

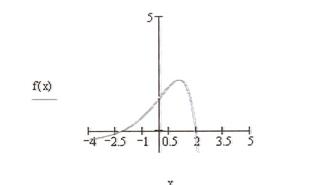
f(x) = (2 – x) (e x ) – 0,5

Рис.2.1. Отделение корней графически

Получили два интервала: [-3; -2], [1,5; 2,5]. Интервал, в котором мы будем уточнять корень – [1,5; 2,5].

2. Уточняем корни. Находим первую производную функции

3. Определяем знакиf(x) на отрезке [1,5; 2,5]:

f(1,5) = 1,741>0, f(2,5) = -6,591 8,801∙ 10 -4 ), значит х₈ = 1,927 является решением нашего уравнения.

п = 0. 10

х₀=а

Рис. 2.2. Проверка критерия достижения

5. Создаем функцию, реализующую вычисления корня уравнения

е х ∙ (2 – х) – 0,5 = 0 на отрезке [1,5; 2,5] с точностью ɛ = 0,001 методом хорд (рис. 2.3). Решением будет являться число 1,927, получившееся на третьем шаге решении

Рис.2.3. Функция, возвращающая значения корня уравнения методом хорд.

Аргументы функции: а, b – концы отрезка; – погрешность вычислений,

f 1pr(x) – функция первой производной

6. Проверяем решение уравнения встроенными функциями Матhcad

хl = root(f(x),x) xl = 1,927

(2 – x)∙(e X ) – 0,5 = 0

x2 = Find(x) x2 = 1,927

Метод касательных

Пример 2.2.

Вычислить методом касательных корень уравнения е х ∙(2 – х) –0,5=0 на отрезке[1,5; 2,5] с точностью ɛ = 0,001.

Решение.

1. Отделяем корни уравнения (см. разд. 2.1).

2. Определяем неподвижную точку.

Для этого определим знаки функции и второй производной на отделенном интервале [1,5; 2,5]. Для этого составим функцию, проверяющую условие неподвижности точки

f(x) = (2 – x)(e x ) – 0,5

Тогда подвижной точкой будет точка а = 1,5.

3. Вычисляем значение итерационной последовательности с использованием рекуррентной формулы метода касательных (рис. 2.4).

х₀ = а

Рис. 2.4.Построение итерационной последовательности

по методу касательных

Анализируя полученные значения для достижения критерия заданной точности, можно сказать, что решением уравнения будет значение

х₄ = 1,927 при п = 4, т.к. 2,367∙10 -5 ˂ 0,001.

4. Создаем функцию, реализующую метод касательных (аналогично методу хорд).

5. Проверяем полученные результаты.

Отметим, что в пакете Mathcad имеется еще несколько функций, позволяющих решать уравнения, например, функция solve, вызываемая с панели Symbolic (рис. 2.5.)

Рис. 2.5. Панель Symbolic

Пример использования команды solve представлен на рис. 2.6.

Рис.2.6. Решение уравнения с помощью команды solve

Метод простой итерации

Пример 2.3.

Решить уравнение 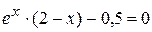методом простой итерации с точностью ɛ = 0,001.

Решение.

Схема решения уравнения методом простой итерации следующая.

1. Отделяем корни.

2. Приводим исходное уравнение к виду х = f(х).

Заменим уравнение 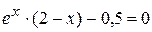уравнением вида .

Здесь величина m должна быть подобрана так, чтобы для функции f(x) выполнились условия 2 и 3 теоремы о достаточном условии сходимости итерационного процесса.

Производная Fˈ(х) на отрезке [1,5; 2,5] отрицательна, следовательно, функция F(х) на этом отрезке монотонно убывает. Ее значения представлены на рис. 2.7.

Рис. 2.7.Значение функции

на отрезке [1,5; 2,5]

Тогда значения функции f(x) будут равны:

Учитывая монотонность функции f(x), из последних равенств легко заметить, что условие 2 указанной теоремы будем заведомо выполнено, если m – правильная отрицательная дробь (рис. 2.8).

Рис.2.8.Определение значения m

Поскольку производная Fˈ(x) на концах интервала [1,5; 2,5] положительна (Fˈ(1,5) = 2,241, Fˈ(2,5) = 18,274) и монотонно возрастает, ее модуль имеет максимум на правом конце отрезка. Тогда если за m принять число , то для любого х из отрезка [1,5; 2,5] значение выражения будет правильной отрицательной дробью. Это обеспечивает выполнение условия 2 теоремы (рис.2.9.).

Для выполнения условия 3 указанной выше теоремы 2.2 найдем производную преобразованной функции

и ее значения на концах отрезка [1,5; 2,5].

Условие 3 теоремы выполнено: значения производных меньше единицы. За величину q возьмем число 0,877 (рис. 2.9.).

Рис. 2.9.Определение значения q

3. Вычисляем значения итерационной последовательности .

В качестве начального значения возьмем, например, начало отрезка, точку х₀ = 1,5.

Критерием достижения заданной точки ɛ = 0,001 при решении нашего уравнения методом простой итерации является величина, равная 1,398∙10 -5 (рис. 2.10).

Рис. 2.10.Определение критерия достижения

заданной точности q

4. Строим итерационную последовательность (рис. 2.11).

x_i = z(x_i-1)

Рис. 2.11.Построение итерационной последовательности

по методу простой итерации

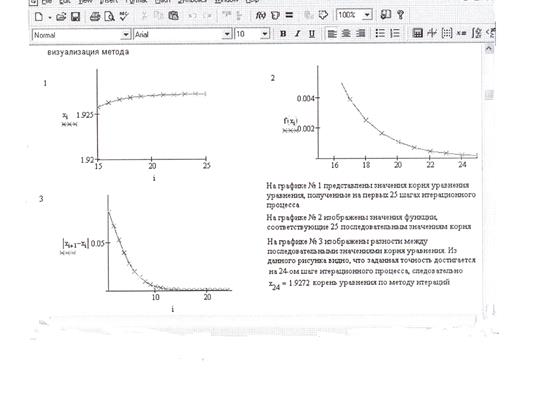
Для 24-го приближения получили, что ˂ 1,398∙ 10 -5 ˂А. Отсюда следует, что х₂₃ = 1,92718 является приближенным решением нашего уравнения.

5. Создаем функцию, реализующую метод простой итерации, для решения уравнения x = f(x) по методу простой итерации (составляется аналогично рассмотренным выше методам).

6. Визуализируем решение уравнения методом простой итерации (рис. 2.12).

Рис. 2.12. Визуализация решения уравнения F(x) = (2 – x)∙e x – 0,5

Вопросы по теме

1. Что значит решить уравнение?

2. Каковы этапы решения уравнения с одной неизвестной численными методами?

3. Какие существуют методы решения с одной неизвестной?

4. В чем заключается этап отделения корней при использовании численных методов решения уравнения?

5. Суть метода хорд. Графическая интерпретация метода.

6. Суть метода касательных. Графическая интерпретация метода.

7. Суть метода простой итерации.

8. Какое уравнение можно решать методом простой итерации?

9. Каковы достаточные условия сходимости итерационного процесса при решении уравнения x = f(x) на отрезке [a, b], содержащего корень, методом простой итерации?

10. Какое условие является критерием достижения заданной точности при решении уравнения x = f(x) методом хорд, касательных, итерацией?

11. Записать формулу нахождения значений последовательности при решении уравнения методом: хорд, касательных.

12. Как строится итерационная последовательность точек при решении уравнения методом простой итерации?

Видео:10 Численные методы решения нелинейных уравненийСкачать

«Лекции.(45 часов) Глава 1. Введение. Методы решения скалярных уравнений. Глава 2. Метод Ньютона решения систем нелинейных уравнений. Глава 3. Решение систем линейных алгебраических . »

Лекции для студентов 2-ого курса, 3-ий семестр

Лекции соответствуют программе общефакультетского курса “Вычислительная математика“, читаемого

на кафедре Информационных систем факультета ПМ-ПУ. Некоторые доказательства и оценки проведены

более подробно, что позволяет лектору отнести их изучение на самомстоятельную работу студентов.

Глава 1. Введение. Методы решения скалярных уравнений.

Глава 2. Метод Ньютона решения систем нелинейных уравнений.

Глава 3. Решение систем линейных алгебраических уравнений.

Глава 4. Методы минимизации значений квадратичной функции.

Глава 5. Введение. Интерполирование функций.

Глава 6. Аппроксимация функций.

Вычислительный практикум.(15 часов) Методические указания по темам вычислительного практикума и зачетные задания разработаны преподавателями кафедры Информационных систем и размещены на сайте этой кафедры.

1. Бахвалов Н., Жидков Н., Кобельков Г. Численные методы. Изд-во “Бином“ 2003.

2. Вержбицкий В.М. Основы численных методов. “Высшая школа“ Москва, 2002.

3. Крылов В.И., Бобков В.В, Монастырский П.И. Начала теории вычислительных методов. Линейная алгебра и нелинейные уравнения. Минск: Наука и техника, 1982.

4. Крылов В.И., Бобков В.В, Монастырский П.И. Начала теории вычислительных методов. Интерполирование и интегрирование. Минск: Наука и техника, 1984.

1. Воеводин В.В. Вычислительные основы линейной алгебры. “Наука“, Москва, 1977.

2. Поляк В.Т. Введение в оптимизацию. “Наука“, Москва, 1982.

Доцент, канд. физ.-мат. наук Сергеев Владимир Олегович Оглавление ВВЕДЕНИЕ 1. Общая постановка задачи. Задачи, корректно поставленные по Адамару. 2. Погрешности решения задач. Представление приближенных чисел. 3. Погрешности вычисления значений функции многих переменных.

Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

1 МЕТОДЫ РЕШЕНИЯ СКАЛЯРНЫХ УРАВНЕНИЙ.

1.1 Метод Чебышева. 1.2 Порядок сходимости метода Чебышева. 1.3 Метод простой итерации решения скалярного уравнения x = f (x).

Видео:Метод простых итераций пример решения нелинейных уравненийСкачать

2 МЕТОД НЬЮТОНА РЕШЕНИЯ СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ.

2.1 Вектор-функция. 2.2 Порядок сходимости метода Ньютона. 2.3 Сходимость метода Ньютона.

Видео:1 3 Решение нелинейных уравнений методом простых итерацийСкачать

3 МЕТОДЫ РЕШЕНИЯ СИСТЕМ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ

СЛАУ. 3.1 Метод Гаусса решения СЛАУ. 3.2 Метод отражений. 3.3 Метод квадратного корня (метод Холецкого). 3.4 Метод окаймления построения обратной матрицы. 3.5 Метод прогонки решения систем с трехдиагональной матрицей. 3.6 Метод простой итерации. 3.7 Метод Зейделя.

Видео:Метод простой итерации Пример РешенияСкачать

4 МЕТОДЫ МИНИМИЗАЦИИ КВАДРАТИЧНОЙ ФУНКЦИИ.

4.1 Квадратичная функция. 4.2 Градиентные методы. 4.3 Метод наискорейшего спуска. 4.4 Метод сопряженных градиентов. 4.5 Метод сопряженных направлений. 4.6 Стационарный многошаговый градиентный метод. 4.7 Полиномы Чебышева. 4.8 Многошаговый стационарный градиентный метод (продолжение). 5 ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ. 5.1 Интерполирование функций алгебраическими полиномами. 5.2 Интерполяционный полином в форме Лагранжа. 5.3 Разделенные разности. 5.4 Интерполяционный полином в форме Ньютона. 5.5 Оценка методической погрешности. 5.6 Выбор узлов интерполирования. 5.7 Разделенные разности и производные функции. 5.8 Численное дифференцирование. Методическая погрешность численного дифференцирования. 5.9 Полная погрешность численного дифференцирования. 5.10 Интерполирование с равноотстоящими узлами. 5.11 Интерполирование с кратными узлами (интерполяционный полином Эрмита). 5.12 Метод построения интерполяционного полинома Эрмита. 5.13 Интерполяционный процесс.

Видео:Численные методы решения нелинейного уравнени Теория Шаговый Метод половинного деления Метод НьютонаСкачать

ВВЕДЕНИЕ

1. Общая постановка задачи. Задачи, корректно поставленные по Пусть заданы два метрические пространства X и Y и отображение F из X в Y. Требуется найти для заданного y такой элемент x, что В большинстве практических задач не всегда явно предполагается, что искомый элемент x принадлежит некоторому подмножеству X, то есть не любой элемент x, удовлетворяющий уравнению F(x) = y, может быть назван решением задачи. Естественно было бы ограничить и множество элементов y : y F(x).

Однако установить принадлежность элемента y этому множеству довольно сложно, к тому же элемент y как правило известен с некоторой погрешностью измерений или произведенных ранее вычислений. Например, если при определении плотности пород, находящихся под поверхностью земли, исходя из измерений гравитационного или магнитного поля на поверхности земли, получены значения плотности 50 г/см3, то такое решение неприемлемо, так как заранее известно, что значения плотности не превышают 20 г/см3.

Итак, для уравнения F(x) = y мы должны прежде всего рассмотреть вопрос о существовании решения задачи в множестве при заданном элементе y.

Пусть для заданного элемента y известно, что решение задачи существует. Второй вопрос: единственно ли это решение? Если решение неединственно, то алгоритм построения решения может и не приводить к определённому результату.

Далее, если решение существует и единственно, то возникает следующий вопрос — вопрос устойчивости этого решения. Пусть элемент y известен с точностью, то есть расстояние Y (y, y ) между заданным элементом y и точным элементом y, не превосходит. Если расстояние между соответствующими решениями x и x стремится к нулю при 0, то говорят, что задача решения уравнения устойчива относительно вариации элемента y. Если отсутствует устойчивость, то требуются специальные методы решения задачи, минимизирующие влияние погрешностей в задании элемента y.

Если для поставленной задачи решения уравнения F(x) = y выполнены условия:

1. решение существует, 2. решение единственно, 3. доказана устойчивость решения, то говорят, что задача поставлена корректно по Адамару.

2. Погрешности решения задач. Представление приближенных Решение корректно поставленной задачи заменяется решением более простой задачи F(x) = y. Такая замена определяет метод решения исходной задачи. Обозначая через x и x решения этих задач, получаем погрешность, которая называется методической погрешностью решения. Она зависит от выбора метода.

Если точное значение элемента y неизвестно, но известно его приближенное значение y, то решения соответствующих задач x и x определяют неустранимую погрешность. Погрешности вычислительных процедур, входящих в решение уравнения F (x) = y должны быть согласованы с точностью задания элемента y и включаются в методическую погрешность.

Сумма методической погрешности и неустранимой погрешности называется полной погрешностью решения задачи.

Пусть число a является приближенным значением величины a : a = a + a. Значение a называется абсолютной погрешностью числа a (в отличие от относительной погрешности |a | ). Конечно, значение a неизвестно, известна только оценка |a| a. Величина a называется оценкой абсолютной погрешности числа a.

Пусть число a представлено в десятичной форме:

где k — цифры, и известна оценка a.

Цифра k называется верной, если a единицы (или половины единицы) k-го разряда в представлении числа a.

Например: a = 0.009823, a = 0.0002.

Цифра 8(k = 4) неверна, так как 0.0002 0.0001.

Цифра 9(k = 3) верна: 0.0002 0.001.

Все цифры, предшествующие верной цифре, верны.

Округление. Число 0.009823 округляется до числа 0.0010. В этом представлении все цифры верные.

После округления в записи числа a следует оставить только верные цифры: a = 0.0010.

Пусть k — первая верная цифра, отличная от 0. Все последующие верные цифры называются значащими.

В примере цифры 1, 0 — значащие цифры. Особенно важно правильное представление приближенных значений чисел в конечных результатах. Например: правильное представление числа x = 3.14158254358 при x = 0.0001 : x = 3.1416.

3. Погрешности вычисления значений функции многих Пусть при вычислении значений функции f (x1, x2. xn ) значения аргументов xi известны с абсолютной погрешностью xi :

Будем предполагать, что в окрестности точки x функция f (x) дифференцируема:

Таким образом, зная величины Bi и оценки абсолютных погрешностей xi, получаем оценку f абсолютной погрешности вычисления значений функции f (x).

Обратная задача. Задана оценка погрешности вычисления значений функции f (x). Требуется определить погрешность xi задания аргументов xi.

Первый способ: все значения xi равны: xi =, Второй способ (метод равных влияний): все значения величин Bi xi равны: Bi xi = 0. Тогда = 0 n, 0 = n и оценки абсолютных величин погрешностей равны xi = nBi.

Видео:Численный метод Ньютона в ExcelСкачать

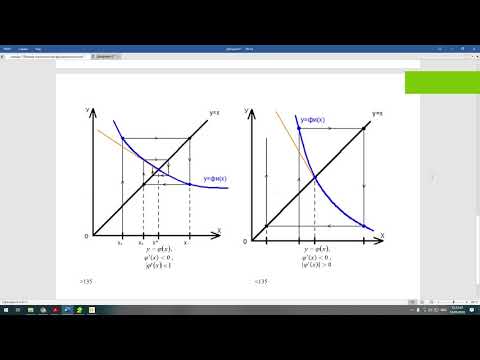
МЕТОДЫ РЕШЕНИЯ СКАЛЯРНЫХ

Постановка задачи. Пусть на [a, b] задана непрерывная функция F(x). Требуется найти значения x [a, b], в которых F(x) = 0. Если значения функции F в точках a и b имеют противоположные знаки, то решение задачи существует. Единственность решения обеспечивается требованием строгой монотонности функции F(x). Если далее предположить, что функция F(x) дифференцируема и |F (x)| 0, то задача решения уравнения F(x) = 0 поставлена корректно по Адамару.

Будем предполагать, что все эти условия выполнены для x [a, b]. Тогда существует обратная функция (y), заданная для значений y, лежащих между значениями F(a) и F(b):

Обратная функция имеет столько же непрерывных производных, сколько и функция F(x).

В методе Чебышева дополнительно предполагается, что функция F имеет на [a, b] (m+1) непрерывных производных.

Взяв произвольное значение y0 из области задания функции, получаем по формуле Тейлора где y лежит между значениями y и y0.

В частности для y = 0:

Значение y0 определим, выбрав произвольно значение x0 [a, b] и положив y0 = F (x0 ).

Тогда Обозначим Тогда Далее взяв в качестве y1 = F(x1 ), получаем Продолжая этот процесс, получим в надежде, что все значения xn [a, b] и что xn x при n.

Ясно, что |x xn+1 | |rm+1 (yn )|.

Этот итерационный метод построения числовой последовательности и называется методом Чебышева решения уравнения F(x) = 0.

Прежде всего отметим, что значения производных yk в точке y = F(x), то есть (F (x)) можно вычислить, зная значения производных функции F(x).

Действительно, согласно определению обратной функции Дифференцируя по x это тождество, получаем y (F(x))F (x) 1, откуда y (F(x)) = (напомним, что |F (x) |).

Дифференцируя последнее тождество по x, получаем Продолжая процесс дифференцирования тождества, получаем последовательно формулы для вычисk ления d (F (x)).

В частном случае при m = 1 метод Чебышева называется методом Ньютона.

В этом методе Рассмотрим уравнение касательной к графику функции F(x) в точке xn : y = F(xn ) + F (xn )(x xn ).

Координата точки пересечения этой прямой с осью x равна xn+1.

Уже для метода Ньютона легко построить примеры, когда xn не стремится к x : метод может “зацикливаться”, т.е. начиная с некоторого N xN +2 = xN Предположим, что все xn [a, b] и что xn x при n. По формуле Тейлора Для оценки величины F(xn ) представим где значение лежит между x и xn. Тогда Предположим, что известна оценка множителя, стоящего перед (x xn )m+1. Тогда Терминология. Пусть построена последовательность элементов xn такая что xn x. Если то говорят, что порядок сходимости равен N.

— если N = 1, то говорят, что метод построения последовательности — метод первого порядка, — если N 1, то говорят о сверхлинейной сходимости, — если N = 2, то получаем метод второго порядка.

Метод Чебышева имеет порядок (m + 1), метод Ньютона — метод второго порядка.

Условия принадлежности xn отрезку [a, b] и условия сходимости метода Чебышева в общем случае трудно проверяемы. Для метода Ньютона эти условия будут получены в следующей главе для более общего случая систем нелинейных уравнений.

1.3 Метод простой итерации решения скалярного уравнения В этом случае F(x) = x f (x). Решения уравнения f (x) = x называются неподвижными точками функции f.

Конечно, можно применить метод Чебышева, но тогда придется вычислять значения производных функции f, что во многих случаях довольно сложно. В предлагаемом методе не требуется вычисления производных.

Метод простой итерации состоит в выборе начального приближения x0, а все последующие приближения x1, x2. вычисляются последовательно правилу: xn+1 = f (xn ).

Каковы перспективы этого метода? Простые примеры показывают, что если |f (x)| 1, то метод простой итерации расходится. В дальнейшем ограничение на f (x) заменяется на более слабое условие.

Пусть в окрестности точки x0 :|x x0 | выполнены условия:

— функция f задана в области, в области функция f (x) удовлетворяет условию Липшица с постоянной L 1 :

— значение m = |f (x1 ) f (x0 )| = |x1 x0 | не превосходит : m и следовательно точка x1.

Найдем соотношения между величинами, L и m, гарантирующие принадлежность всех xn области, существование неподвижной точки x функции f в области и сходимость xn x.

(L + 1)m. Потребуем, чтобы (L + 1)m, тогда x2.

Легко показать, что если |xn xn1 | Ln1 m и |xn x0 | (1 + L + L2 +. + Ln2 + Ln1 )m, то Таким образом, если для чисел m, и L выполнено неравенство то все xn.

Оценим Тогда при n |xn+k xn | 0 и последовательность сходится в себе. В силу полноты пространства R1 (признак Коши) существует предел последовательности xn x при n. Так как все Из непрерывности функции f получаем f (x ) = lim f (xn ) = lim xn1 = x, следовательно точка x n n неподвижная точка функции f (x), принадлежащая области.

Легко убедиться, что x — единственная неподвижная точка: если x и x — две неподвижные точки, то Таким образом верна Теорема. Пусть в области : |x x0 | функция f (x) задана и удовлетворяет условию Липшица с постоянной L 1.

Если m (1L), где m = |f (x0 )x0 |, то все xn и метод простой итерации сходится к единственной неподвижной точке x и верна оценка Последняя оценка получена предельным переходом в неравенстве Терминология. Если для итерационного метода получена оценка:

то xn x, и говорят что метод сходится со скоростью геометрической прогрессии со знаменателем q.

В условиях доказанной теоремы метод простой итерации сходится со скоростью геометрической прогрессии со знаменателем L:

Видео:Численное решение уравнений, урок 3/5. Метод хордСкачать

МЕТОД НЬЮТОНА РЕШЕНИЯ

Видео:Метод хордСкачать

СИСТЕМ НЕЛИНЕЙНЫХ

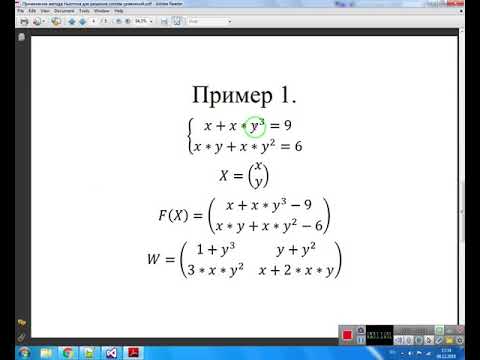
Рассматривается система n нелинейных уравнений относительно неизвестных x(x1, x2. xn ) Rn. Мы не будем различать точки x Rn и векторы x Vn. Введем вектор-функцию y = F (x) :

Тогда систему уравнений можно записать в виде F (x) = 0.

Метод Ньютона основан на представлении каждой функции fi (x) в виде Матрица определяет линейный оператор в векторном пространстве Vn. Обозначим этот оператор F (x ), получим представление вектор-функции F (x) в виде:

Для предполагаемого решения x системы получаем Пренебрегая вектором r(x, x0 ), получаем «приближенное»решение x1 системы как решение системы линейных алгебраических уравнений с матрицей n.

Далее строится вектор x2 как решение СЛАУ и все последующие векторы x3, x4. xk+1. строятся как решения xk+1 линейных алгебраических систем Возникают следующие вопросы:

— разрешимы ли эти системы?

— принадлежат ли эти решения области ?

— сходится ли последовательность векторов к решению x ?

— единственно ли это решение в области ?

Для вектора x Vn обозначим Число x называется нормой вектора x. Расстояние между векторами x и y определим как последовательность векторов xk сходится к вектору x, если xk x 0 при k.

Для вектора F (x) норма F (x) = max |fi (x)|; норма если частные производные функции fi (x) непрерывны.

Для матрицы A = n Эта величина называется нормой матрицы A. Верно неравенство:

Рассмотрим матрицы F (x) (линейные операторы в векторном пространстве Vn ), вычисленные в точках Определение. Говорят, что оператор F (x) удовлетворяет условию Липшица с постоянной L, если Пусть оператор F (x) удовлетворяет условию Липшица. Так как матрица При фиксированных векторах x и x значение fi (x + x) являются функцией от : fi (x + x) = i (). Дифференцируя эту сложную функцию Оценим Таким образом верна оценка:

Эта оценка позволяет определить порядок малости норм r(x0, x ), r(x1, x ). r(xk, x ). при построении метода Ньютона.

Для непрерывной вектор-функции F (x) рассмотрим последовательность векторов, построенных по правилу с начальным вектором x0. Если существует lim xk, k, то по непрерывности функции F (lim xk ) = 0.

Пусть Bk — последовательность линейных операторов, таких что существуют обратные операторы Bk.

Образуем новую последовательность векторов xk :

Для векторов xk этой последовательности выполнены равенства Если эта последовательность имеет предел x, то F (x ) = 0.

В методе Ньютона выбирают Bk = F (xk ) :

и для этой последовательности При изучении сходимости метода Ньютона будем предполагать:

— операторы F (x) удовлетворяют условию Липшица, — нормы операторов [F (x)]1 ограничены: [F (x)]1.

Порядок сходимости метода устанавливается в предположении, что xk x при k. Сравним величины xk x и xk+1 x.

Введем вектор y :

Так как оператор F (xk ) имеет обратный, то x xk+1 = [F (xk )]1 y.

Оценим y. Так как F(x ) = 0, то и согласно оценке () Тогда и следовательно метод Ньютона — метод второго порядка.

Пусть выбрано начальное приближение x0 и x0 внутренняя точка области.

Теорема. Пусть в области : x x0 операторы F (x) удовлетворяют условию Липшица в постоянной L, существуют обратные операторы [F (x)]1 и [F (x)]1.

Тогда если Доказательство проводится аналогично доказательству сходимости метода простой итерации решения скалярного уравнения.

Легко устанавливаются неравенства обеспечивающие принадлежность точек xk. Из сходимости в себе последовательности получаем существование предела последовательности и оценку x xk.

Замечание. При дополнительном условии L 1 решение x системы единственно в области.

Видео:Алгоритмы С#. Метод Ньютона для решения систем уравненийСкачать

МЕТОДЫ РЕШЕНИЯ СИСТЕМ

Видео:Метод касательных (метод Ньютона)Скачать

ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ

Видео:2.2 Итерационные методы решения СЛАУ (Якоби, Зейделя, релаксации)Скачать

УРАВНЕНИЙ СЛАУ.

Видео:Метод ЭйлераСкачать

ВВЕДЕНИЕ

1. Линейные векторные нормированные пространства.

В этой главе рассматриваются вещественные линейные векторные пространства. В этих пространствах вводятся различными способами метрика. Как правило метрика определяется нормой x вектора x :

и мы получаем полное нормированное векторное пространство.

Обычно рассматриваются три нормированные пространства, в которых норма вектора x(x1, x2. xn ) равна:

Для любых этих пар нормированных пространств верны неравенства (эквивалентность норм):

где постоянные C1 и C2 зависят от выбора пространств и от размерности вектора x, но не зависят от выбора вектора x.

Ясно, что Таким образом Если установлено, что последовательность сходится к x в одной норме, то она сходится к x в любой другой норме.

2. Линейные операторы в нормированных пространствах. Нормы матриц, нормы операторов.

Линейные отображения (линейные операторы) в n-мерном векторном пространстве Vn определяются квадратными матрицами A :

Рассматривая для вектора x и вектора y разные нормы, мы получим линейные отображения из одного нормированного пространства в другое нормированное пространство. Мы будем предполагать, что для x и Ax выбраны одинаковые нормы: нормы x и Ax согласованы.

Рассмотрим множество S1 векторов, нормы которых равны 1. Координаты этих векторов ограничены.

Координаты векторов Ax и значения Ax являются непрерывными функциями координат вектора x.

Тогда существует sup Ax и этот супремум достигается: sup Ax = max Ax.

В силу линейности оператора A :

Легко показать, что верны неравенства Вычисление норм матриц.

Пусть max Ax 2 = (Ax, Ax) = (A Ax, x) 0. Матрица A A симметричная, положительная и её собственные числа µn вещественны и неотрицательны:

Обозначим через 1, 2. n соответствующие им собственные векторы:

Ясно, что Для вектора n S1 норма An 2 = µ. Таким образом A 2 = |m |, где m — максимальное по модулю собственное число матрицы A.

Эквивалентность норм матрицы.

Исходя из эквивалентности норм вектора, легко получить неравенства В частности 3.Числа обусловленности матрицы.

Пусть матрица A имеет обратную матрицу A1. Рассмотрим две системы Ax = y и Ax = y + y, где y вариация (погрешность) вектора y. Вариация решения x = A1 y. Рассмотрим относительную погрешность решения x и относительную погрешность y правой части:

Число (A) = A1 A называется числом обусловленности матрицы A в выбранной метрике.

Свойства числа обусловленности 1. (A) 1. Так как в любой норме E = 1, то 3. Оценка снизу числа обусловленности матрицы. Рассмотри векторы x и y = Ax и векторы x и y = Ax. Тогда отношение 4. В оценке x C y значение C = (A) уменьшить нельзя.

Действительно, рассмотрим вектор y, такой что A1 y = Если (A) 1, то говорят, что матрица А и система уравнений Ax = y плохо обусловлены.

Пример единственное решение.

Рассмотрим x = (0, 0. 0, 1), и y = Ax = (1, 1. 1, 1).

Пусть y = (0, 0. 0, ), y =. Тогда x = (2n2, 2n3. 2, 1, 1). x = 2n2.

Для числа обусловленности получаем оценку (A) 2n2 (n = 32). Таким образом матрица A и система уравнений плохо обусловлены. Заметим, что из неравенства A A1 (A) получаем 4. Матрицы с диагональным преобладанием.

Определение: матрица A = n i,j=1 называется матрицей с диагональным преобладанием, если для всех i = 1, 2. n верно Например матрица 3 6 1 — матрица с диагональным преобладанием, = 2.

Доказательство. Рассмотрим любой ненулевой вектор x. Его норма x = max |xi | = |xm |. Вычислим y = Ax.

Тогда Таким образом для любого решения системы Ax = y верно неравенство:

Рассмотрим однородную систему Ax = 0. Предположим, что она имеет ненулевое решение x0. Но в силу полученного неравенства x = 0. Следовательно, решение системы Ax = y существует и единственно при любой правой части, и матрица A имеет обратную матрицу. Далее В этой части мы рассмотрим методы, которые доставляют точные решения систем за конечное число операций. Предполагается, что обратная матрица существует и что все вычисления производятся точно.

Составим расширенную матрицу A+ системы Ax = y:

Первый шаг. Потребуем, что a11 = 0 (главный минор 1 первого порядка матрицы A). Разделим первую строчку матрицы A+ на a11 :

Потребовалось (n1) делений элементов первой строчки матрицы A и одно деление первой координаты вектора y.

Умножим полученную строчку на a21 и вычтем из второй строчки матрицы A+ : получим новую вторую строчку:

Значение a22 a12 a21 = 2, где 2 главный минор матрицы A второго порядка. Потребуем, что 2 = 0.

Продолжая этот процесс, получим матрицу A1, первый столбец которой равен (1, 0. 0)T и вектор y 1 :

Первый столбец матрицы L1 равен ( a1, a21, · · ·, an1 )T, её диагональные элементы равны a1, 1. 1, остальные элементы равны 0. Матрица L1 нижняя треугольная матрица. Обратная матрица L1 тоже ниж- няя треугольная, её первый столбец (a11, a21. an1 )T, диагональные элементы равны a11, 1. 1; det L1 = a11, det L1 = a11.

Для построения матрицы A1 требуется (n1)n операций деления и умножения, для построения вектора y 1 потребовалось n таких операций.

Второй шаг. Рассматривается вторая строчка матрицы A+ и строится матрица L2 размерности n n, такая что в матрице A2 = L2 A1 первый столбец совпадает с первым столбцом матрицы A1, а второй столбец равен ( a11, 1. 0, 0)T. Для построения матрицы A2 потребуется (n 1)(n 2) операций, а для построения вектора y 2 = L2 y 1 потребуется (n 1) операций. Матрицы L2 и L1 нижние треугольные;

det L2 = 2, det L1 = 1.

После проведения n таких шагов в предположении, что все главные миноры матрицы i = 0 (в том числе det A = 0), получим верхнюю треугольную матрицу U, на диагонали которой стоят 1: U = Ln Ln1. L2 L1A = LA и вектор y n = Ly; det Lk = k1, det L1 = k1.

Система U x = y эквивалентна системе Ax = y, система Ax = y эквивалентна LAx = Ly.

Ясно, что A = L1 U, матрица L1 — нижняя треугольная, det L1 = det A.

Таким образом, метод Гаусса состоит в представлении матрицы A в виде произведения нижней треугольной матрицы и верхней треугольной матрицы U, на диагонали которой стоят 1.

Найдем число операций, необходимых для построения матрицы U и для построения вектора y n = Ly.

Для построения матрицы U потребовалось n(n + 1) + (n 1)(n 2) +. + 2 + 0 = (n1)n(n+1) операций.

Для построения вектора Ly потребовалось Решение системы Ax = y. Для вычисления xn не требуется никаких операций, для получения xn потребуется одна операция, для xn2 две операции, для вычисления x1 потребуется (n 1) операций.

Для построения решения потребуется n(n 1) 1 операций.

Для решения системы Ax = y методом Гаусса потребуется (n1)n(n+1) Теорема. Пусть все главные миноры матрицы A отличны от 0. Тогда метод Гаусса состоит в представлении матрицы A в виде произведения нижней треугольной матрицы L и верхней треугольной матрицы U с единичной диагональю A = LU.

Число операций умножения-деления равно n (n2 + 3n 1) n.

1. Для построения матрицы L1 требуется столько же операций, сколько и для построения матрицы U. Так как то для вычисления определителя матрицы A по методу Гаусса потребуется число операций порядка n.

Вычисляя определитель непосредственно разложением по элементам первой строчки получим необходимое число умножений порядка N = (e 1)n!

2. Построение обратной матрицы.

Построив матрицы U, L1 решим n систем уравнений Учитывая простую структуру правых частей ei, получим, что необходимое число операций для построения A1 равно n3 n n n3, т.е. примерно в три раза большее, чем решение одной системы Ax = y.

1. Метод Гаусса- метод последовательного исключения неизвестных.

2. Получив на каждом шаге новую матрицу Ai, следует найти или наибольший по модулю элемент в новой строчке, или наибольший по модулю элемент в новом столбце, или наибольший по модулю элемент в оставшейся матрице (ведущие элементы). Изменив порядок нумерации переменных или изменив порядок нумерации строк, или и то и другое, поставим ведущий элемент в верхний левый угол оставшейся матрицы.

Эти процедуры уменьшают влияние ошибок вычисления.

Одновременно снимаются и ограничения на главные миноры исходной матрицы, оставив лишь условие n = detA = 0.

3. Несложно построить метод, в котором матрица преобразуется в единичную матрицу (метод Жордана).

1. Преобразование отражения.

Зададим вектор w, w = 1. Вектор w определяет плоскость P l, ортогональную вектору w. Понятие ортогональности определенно только в векторном пространстве с нормой x = x 2 — в векторном конечномерном пространстве Гильберта. Используя понятия этого пространства, представим любой вектор x в виде ортогонального разложения:

Определим вектор W (x) = pw x+pP l x. Ясно, что отображение аддитивно и однородно. Следовательно, это преобразование определяется матрицей W размерности (n n).

Свойства матрицы W :

-W (W x) = x и W W = E, W 1 = W, т.е. матрица W ортогональная.

Построим матрицу W. Ясно, что x W x = 2pw x и W x = x 2pw x.

Обозначим координаты вектора x = x(x1, x2. xn ) и вектора w = w(w1, w2. wn ). Получаем W x = Обозначим матрицу V = n. Матрица V симметричная матрица, тогда и матрица W = E 2V i,j= симметрична. Мы получаем ещё одно свойство матрицы W :

2. Метод отражений решения СЛАУ.

Метод состоит в построении последовательности преобразований отражения с целью получить эквивалентную систему с верхней треугольной матрицей.

Первый шаг. Пусть a первый столбец матрицы A и a11 = 0. Построим вектор w, такой что W (a) = e1.

Так как W (a) = a 2(w, a)w, то эта задача сводится к определению w и числа из условия Если (w, a) = 0, то вектор a коллинеарен вектору e1, и следует перейти ко второму шагу. В случае (w, a) = 0, получаем:

(т.е. вектор w есть линейная комбинация векторов a и e1 ).

Из этого равенства получаем Обозначим скалярное произведение (w, a) =. Тогда Так как W a = a, то для || получаем: || = a. Для того, чтобы величина 22 была положительна, выберем и величина известна. Взяв, например, положительное значение вычислим вектор w :

Остается проверить, что w =1:

Обозначим полученный вектор w через w1, обозначим = 1, преобразование отражения W через W1.

Второй и последующие шаги состоят в последовательном построении преобразований Wm, таких что элементы m-го столбца матрицы Am = Wm Am1 равны 0 при i m, а при i = m элемент отличен от 0. В результате получим верхнюю треугольную матрицу U : U = Wn Wn1. W1 A.

Обозначим Wn Wn1. W2 W1 = W ; W A = U.

Матрица W ортогональна:

Матрицы W в общем случае несимметрична: произведение симметричных матриц в общем случае не является симметричной матрицей.

Из равенства W A = U получим A = W 1 U. Матрица W 1 ортогональная: W 1 = W. Таким образом, метод отражений состоит в представлении матрицы A в виде произведения ортогональной матрицы и верхней треугольной матрицы.

Вычисление решения системы сводится к решению системы U x = W y и производится аналогично обратному ходу метода Гаусса.

Ясно, что как и в методе Гаусса, изменение нумерации строк или столбцов позволяет применить метод отражений только при одном условии:

Число операций в методе отражений 3n, метод более устойчив к вычислительным ошибкам.

Этот метод предназначен для решения систем с симметричной матрицей A, главные миноры которой отличны от 0.

Матрица A представляется в виде произведения трёх матриц где S верхняя треугольная матрица (S нижняя треугольная), а матрица D- диагональная матрица, на диагонали которой стоят числа 1 и 1.

Построение матриц S и D.

Обозначим элементы матрицы S : sij, sij = 0, если i j. Диагональные элементы матрицы D обозначим через d1, d2. dn.

Элементы матрицы DS равны n, элементы матрицы S DS равны так как ski = 0 при k i. Равенство (S DS) = A приводит к условиям Первый шаг: для первой строки i = 1 :

s11 d1 s1j = a1j (j = 1, 2. n), и при j = 1 получаем Из равенств s11 d1 s1j = aij получаем и все элементы первой строчки матрицы S найдены.

Второй шаг: для i = 2 s12 d1 s1j + s22 d2 s2j = a2j, (j = 2, 3. n) и при j = 2 :

Значение d2 выберем из условия s2 0, т.е. d2 = sign(a22 s2 d1 ).

Тогда s2 = |a22 s2 d1 | и s22 = |a22 s2 d1 |.

Покажем, что s22 0 : s2 = |a22 s2 d1 | = |a22 a12 | = | 1 | 0 и s22 строго больше нуля. Далее из равенств s22 d2 s2j = a2j s12 d1 s1j находим все элементы второй строчки матрицы S.

Аналогичным способом рассматривая строчки i = 3, 4. n, получаем последовательно числа di, числа sii 0 и все элементы i-той строчки матрицы S.

Решение СЛАУ. Ax = y. S DSx = y. Обозначим DSx = z. Тогда S z = y система с нижней треугольной матрицей, диагональные элементы которой sii 0. Решение z этой системы легко получить.

Решение x исходной системы найдем как решение системы DSx = z с верхней треугольной матрицей, диагональные элементы которой отличны от нуля.

3.4 Метод окаймления построения обратной матрицы.

Метод окаймления состоит в последовательном построении обратных матриц, соответствующих главным минорам матрицы A. Поэтому предполагается, что все главные миноры матрицы отличны от нуля.

Матрица A1 = a11 размерности 1 1 имеет обратную:

Предположим, что для матрицы Am1 размерности (m 1) (m 1) с определителем m1 = обратная матрица A1 уже построена (например при m = 2).

Построим обратную матрицу для матрицы Am, det Am = m = 0.

Представим матрицу Am и матрицу A1 в блочном виде: m столбцы, uT, sT — вектор-строчки.

Из (1) : Bm1 + A1 vsT = A1 и Bm1 = A1 (Em1 vsT ).

Покажем, что am uT A1 v = 0. СЛАУ с матрицей Am имеет единственное решение при любой правой части. Запишем матрицу Am в блочном виде, в правой части возьмем вектор, у которого только координата ym отлична от нуля:

Последнее уравнение системы имеет вид Сравнивая эти два полученные уравнения, получаем:

Так как координата xm определяется однозначно при любом значении ym, то величина am uT A1 v = Итак, продолжая процесс построения матриц A1, построим и матрицу A1. Число операций равно n3.

Замечание. Пусть в математическую модель кроме параметров x1, x2. xn вводится еще один параметр xn+1, значение которого неизвестно. В случае линейных моделей получаем матрицу An+1. Метод окаймления позволяет получить матрицу A1, исходя из уже построенной матрицы A1 за (3n2 + 3n 1) операций.

3.5 Метод прогонки решения систем с трехдиагональной Рассматривается СЛАУ с матрицей размерности (n + 2) (n + 2) :

К решению таких систем сводится например задача приближенного решения граничной задачи для линейного дифференциального уравнения второго порядка с переменными коэффициентами:

Обозначим h = n+1, xi = ih, неизвестные значения u(xi ) = ui, значения F (xi ), A(xi ) обозначим Fi, Ai.

Считая, что получим систему:

или Эта система — система с трехдиагональной матрицей:

Для решения систем с трехдиагональной матрицей можно, например, применить метод Гаусса. Учитывая особенности матрицы, можно существенно упростить процесс построения решения.

Будем искать значения xi в виде где i+1 и i+1 неизвестные коэффициенты.

Тогда xi1 = i xi + i. Из i-того уравнения системы исключим xi1 : ai (i xi + i ) ci xi + bi xi+1 = fi и в представлении значений xi :

Значения 1 и 1 получим из первого уравнения системы, при i = 0: x0 + 1 x1 = µ1. Следовательно, 1 = 1, 1 = µ1. Значения 2, 2 получим последовательно Коэффициенты i, i i = (1, 2. n + 1) называются прогоночными коэффициентами.

Решение системы xi получим (обратный ход), рассматривая сначала последнее уравнение системы (i = n + 1):2 xn + xn+1 = µ2 вместе с представлением xn = n+1 xn+1 + n+1. Отсюда получим Значения xn, xn1. x0 вычислим последовательно:

При вычислении xi мы замечаем, что если значения |i | 1, то при большой размерности системы погрешности в задании правых частей системы и погрешности значений xi будут возрастать, т.е. процесс вычисления xi будет неустойчивым относительно погрешности вычислений. Поэтому, кроме условий ci i ai, 1 2 n+1 = 0, желательно ввести требование |i | 1.

Доказательство. Так 1 = 1, то |1 | 1. Далее величины Замечание. Рассмотренный метод прогонки называется методом верхней прогонки. Если исходить из начального представления в виде xi = i1 xi1 + i1, то получим метод нижней прогонки. Можно построить и методы встречных прогонок.

Построение итерационных методов.

Для СЛАУ Ax = y рассмотрим итерационный процесс xk+1 xk + Axk = y, т.е. xk+1 = xk (Axk y) при 0.

Если последовательность векторов имеет предел x, то Ax = y и x — решение системы.

Пусть Bk — неособые матрицы и матрицы Bk легко строятся.

Тогда Bk + Axk = y, и мы получаем итерационный процесс:

Матрица S- матрица перехода. Если системы.

Рассматривается система Ax = y, где матрица E B :

Задавая вектор xo построим вектор x1 = Bx0 + y и далее xk = Bxk1 + y.

Ясно, что верна теорема:

Теорема. Если B = q 1, то существует единственное решение x, последовательность стремится к x со скоростью геометрической прогрессии для любого начального вектора x0.

Доказательство. Рассмотрим однородную систему x = Bx. Для её решения верно неравенство x = Bx B x = q x. Тогда x = 0. Следовательно, решение исходного уравнения существует и единственно при любой правой части y.

Замечание. Полученная оценка называется априорной оценкой, так как вектор x неизвестен. Однако, зная xk1 и xk, легко получить так называемую апостериорную оценку:

Система x = Bx + y имеет специальный вид. Для СЛАУ с симметричной положительной матрицей можно рассмотреть систему x (E µA)x = µb. Если собственные числа матрицы A равны 0. n, собственные числа матрицы равны 1 µi, и норма матрицы E µA E µA 2 = max |1 µi |.

Взяв µ = n +1, получим, что |1 n +1 | 1. Тогда итерационный процесс xk+1 = xk + (E µA)xk + µb сходится.

Для произвольной матрицы A можно рассмотреть СЛАУ A Ax = A y и построить для этой системы указанный итерационный процесс. Но следует иметь ввиду, что число обусловленности (A A) увеличивается:

Будем предполагать, что диагональные элементы матрицы A отличны от нуля. Матрицу A представим в виде где матрица D — диагональная матрица, матрицы L и U нижняя и верхняя треугольные матрицы с нулевыми диагоналями.

Метод Зейделя состоит в задании начального вектора x0 и в последовательном вычислении векторов Тогда При реализации этого метода не требуется строить матрицу (L + D)1.

a11 xk+1 = (a12 xk + a13 xk +. + a1n xk ) + y1, получаем xk+ a21 xk+1 + a22 xk+1 = (a23 xk +. + a2n xk ) + y2, получаем xk+

an1 xk+1 + an2 xk+1 +. + ann xk+1 = yn, получаем xk+ и таким образом строим xk+1.

Вариантами метода Зейделя являются методы релаксации с выбором параметра релаксации (0, 2). При (0, 1) получаем методы нижней релаксации, при (1, 2) — методы верхней релаксации. Наиболее употребительны методы верхней релаксации.

Сходимость метода Зейделя легко доказывается, например в предположении, что матрица A — матрица с диагональным преобладанием: |aii | |aij | 0 для всех i.

В этом случае Глава

Видео:2.1 Точные методы решения СЛАУ (Крамера, Гаусса, Жордана, прогонки)Скачать

МЕТОДЫ МИНИМИЗАЦИИ

Видео:10 Метод Ньютона (Метод касательных) C++ Численные методы решения нелинейного уравненияСкачать

КВАДРАТИЧНОЙ ФУНКЦИИ.

Пусть f (x) непрерывная функция, отображающая множество D Rn в множество R1. Ставятся две задачи:

-найти inf f (x), x D -найти точку x D, такую что f (x) f (x ), x D.

В этой главе рассматриваются методы решения этих задач на простом примере минимизации квадратичной функции. Одновременно строятся и методы решения систем линейных алгебраических уравнений с положительно определенной матрицей.

Функция где точки x(x. xn ) Rn, (D = Rn ) называется квадратичной функцией.

Мы не будем различать точки x Rn и векторы x Vn с составляющими (x1, x2. xn ). Введя в Vn скалярное произведение, получим где матрица A симметрична. Собственные числа i матрицы A вещественны и 0 i n.

В этой главе рассматриваются матрицы A, имеющие обратные матрицы. Тогда 1 0, 1 2.

Значения собственных чисел i как правило неизвестны, но на практике известны оценки 1 m 0, Значения |f (x)| при неограниченном росте x неограниченно возрастают, так как (Ax, x) 1 x 2, а значения |(b, x)| имеют порядок роста x. Таким образом inf f (x) может достигаться на ограниченном множестве.

Рассмотрим Пусть x0 — любой вектор. Если Ax0 + b = 0, то в точке x0 нет ни максимума, ни минимума: и при малых значениях x знак разности f (x0 + x) f (x0 ) определяется знаком (Ax0 + b, x), и при замене x на x знак f (x0 + x) f (x0 ) меняется на противоположный. Поэтому точка x0 не может быть точкой экстремума функции f (x). Таким образом, единственная точка экстремума функции f (x) является единственным решением x системы линейных алгебраических уравнений В точке x f (x + x) f (x ) = 1 (Ax, x) 0, следовательно точка x единственная точка минимума функции f (x).

1. Из равенства согласно определению производной отображения f в точке x, получаем что вектор Ax + b определяет линейный оператор f (x) действующий из Vn в R1 по формуле 2. Дифференцируя функцию f (x) = f (x1, x2. xn ) по координатам xi, получаем и Ax + b = grad f (x) и вектор grad f (x) будем обозначать r(x) :

Вектор grad f (x) = r(x) определяет направление наискорейшего возрастания значений f (x) в окрестности точки x, а вектор r(x) определяет направление наискорейшего убывания этих значений.

Методы минимизации значений функции f (x) в соответствии с поставленными задачами можно также разделить на две группы:

— близость точки x к точке x оценивается величиной x x, — близость точки x к точке x оценивается значениями f (x) f (x ).

В обоих случаях используются градиенты функции f (x), но методы первой группы называются градиентными методами, а методы второй группы — методами спуска.

Пусть выбран начальный вектор x0. Векторы xk строятся последовательно по правилам xk+1 = xk (Axk + b), 0. Вектор r(xk ) = Axk + b обозначим rk : rk = Axk + b.

Возникает вопрос: как выбрать значение ?

Оценим известны только оценки m и M, то в этих оценках следует заменить 1 на m, а n на M.

Таким образом, при (0, 2 ) градиентный метод сходится к точке x со скоростью геометрической прогрессии:

(при = 0 значение q = n +1 ).

В этом методе величина (шаг по направлению антиградиента) в итерационном процессе xk+1 = xk rk выбирается из условия минимума значения f (xk+1 ).

Согласно (2): f (xk+1 ) = f (xk rk ) = f (xk ) (Axk + b, rk ) + 1 (Ark, rk ) = Значение находим из условия () = 0 :

и оптимальное значение :

Метод наискорейшего спуска строится по правилу Вычислим (rk+1, rk ) = (Axk+1 + b, rk ) = (A(xk k rk ) + (b, rk )) = Axk + b Таким образом, в методе наискорейшего спуска векторы rk и rk+1 ортогональны: (rk+1, rk ) = 0.

Построим векторы pk = xk xk1, где вектор xk построен по методу наискорейшего спуска. Тогда (rk+1, pk ) = (rk+1 k rk ) = k (rk+1, rk ) = 0.

Тогда в методе наискорейшего спуска векторы rk+1 и pk ортогональны:

Сходимость метода наискорейшего спуска.

Рассмотрим последовательность векторов , полученную по методу наискорейшего спуска с начальным вектором x0 :

Ясно, что оптимальным значением = 0. Ясно, что Вектор xk x представим в виде линейной комбинации собственных векторов i матрицы A:

Из неравенства f (xk+1 ) f (x ) f (yk+1 f (x )) следует Тогда и последовательность f (xk ) сходится к f (x ) со скоростью геометрической прогрессии со знаменателем q 2, где Апостериорная оценка f (xk ) f (x ).

Апостериорная оценка xk x по значениям f (xk ) и f (xk+1 ).

Сходимость xk к x.

Из свойств матрицы A следует Таким образом xn x со скоростью геометрической прогрессии со знаменателем q.

Пусть x0 начальный вектор. Вектор x1 построим по методу наискорейшего спуска:

x1 = x0 0 r0 (если r0 отличен от нулевого вектора, то 0 = 0), и вычислим векторы r1 = Ax1 + b, p1 = x1 x0. Эти векторы ортогональны. Любой вектор и в частности вектор x x1 можно представить в виде ортогонального разложения x x1 = r1 + p1 + z, где z p1, z r1.

Метод сопряженных градиентов начинается с минимизации значений функции f (x) на гиперплоскости x = x1 r1 + p1. Значения функции Естественно предполагать, что векторы r1 и p1 отличны от нулевого вектора. Ясно, что минимум функции f (x) на гиперплоскости существует и единственен. Условия минимума функции f (x) :

Эту систему можно записать в виде Решение системы существует и единственно: = 1, = 1 и величина 1 0.

Обозначим векторы и в силу системы получаем свойства векторов r2 и p1 :

Вычислим величину (r0, r2 = 0) = ( 0 (x1 x0 ), r2 ) = 0 (p1, r2 ) = 0.

Таким образом векторы r1, r1, r2 попарно ортогональны. Для векторов p2 и p1 получаем:

В методе сопряженных градиентов последовательно строятся векторы Если окажется, что вектор rk нулевой, то Axk = b и xk = x. В этом случае итерационный процесс заканчивается.

Коэффициенты k и k находятся из условия минимума значений функции f (xk + rk + pk ). Из получаемой системы двух линейных уравнений для и получаем единственное решение = k и = k.

Ясно, что значение k 0. Свойства этого решения можно записать в виде: (rk+1, rk ) = 0, (rk+1, pk ) = 0.

Теорема. Ненулевые векторы r0, r1, r2. rk попарно ортогональны.

Доказательство. Предположим, что теорема верна для r0, r1, r2. rk. (при k = 2 она верна), построим вектор rk+1.

На предыдущих шагах (при i = 1, 2. k 1) ri+1 = ri i Ari + Так как значение i = 0, то Ari = i (ri+1 ri i (ri ri1 )), т.е. вектор Ari есть линейная комбинация векторов (ri1, ri, ri+1 ).

Вычислим (rk+1,, ri ) для i = (1, 2. k 2) : (ri, rk+1 ) = (ri, rk ) k (ri, Ark ) + k (ri, rk rk1 ) = k (ri, Ark ) = k (rk, Ari ) = k (rk, L(ri1, ri, ri+1 )) = При i = 0 величина (rk+1, r0 ) = k (r0, Ark ) + k (r0, rk rr1 ) = = k (rk, r10 0 ) = 0 и вектор rk+1 ортогонален всем векторам r0, r1. rk2.

При i = k согласно свойству решения системы уравнений для k, k получаем ортогональность векторов kk+1 и rk.

Остается показать, что (rk+1, rk1 ) = 0. Вектор pk = k1 + k1 pk1 = =. = L(r0, r1. rk1 ). Согласно свойству системы для k и k получаем и векторы r0, r1. rk, rk+1 попарно ортогональны. Теорема доказана.

В векторном пространстве Vn существует не более n линейно независимых векторов. Если векторы r0, r1. rn1 ненулевые, то вектор rn — нулевой вектор и вектор xn = x.

Следовательно, метод сопряженных градиентов приводит к вектору x за конечное число итераций, не превосходящее (n 1).

Построенный итерационный процесс позволяет найти решение СЛАУ Ax = b с симметричной положительно определенной матрицей A за конечное число операций и поэтому может быть отнесен к числу точных методов решения таких систем.

Замечание. Для ненулевых векторов pi и pj верно (Api, pj ) = 0 при i = j, а при i = j (Api, pi ) = 0.

Действительно (Api, pj ) = (ri ri1, L(r0, r1. rj1 )) при i j. С другой стороны (Api, pj ) = (pi, Apj ) = (Apj, pi ) = 0 при j i. Значение (Api, pi ) pi 2 0.

1. A-ортогональные системы векторов.

Пусть A симметричная положительно определенная матрица размерности n n.

Определение. Система ненулевых векторов векторного пространства Vn называется Aортогональной, если (Asi, sj ) = 0 при i = j, а (Asi, si ) = 0.

Векторы А-ортогональной системы линейно независимы. Действительно, если si = c1 sk +c2 sm, i = k, m, то (Asi, si ) = (Asi, c1 sk, c2, sm ) = 0.

Если известна А-ортогональная система, то решения СЛАУ Ax = b легко построить: так как любой Тогда А-ортогональную систему можно получить исходя из любой линейно независимой системы векторов .

Коэффициенты kj находим из условий:

2. Метод сопряженных направлений.

Пусть задана А-ортогональная система векторов . Для минимизации значений функции f (x) = 1 (Ax, x) + (b, x) рассмотрим итерационный процесс:

где вычисляется из условия min f (s1 ), т.е. из условия xk строится в виде xk = xk1 + sk. Из условия min f (xk ) получаем Для k = n получаем Следовательно вектор x получается за конечное число итераций, определяемое числом скалярных произведений (b, sk ), отличных от нуля. Метод сопряженных направлений, как и метод сопряженных градиентов следует отнести к числу точных методов решения СЛАУ Ax = b.

Замечание. В методе сопряженных градиентов векторы p1, p2. отличные от нуля образуют А-ортогональную систему.

4.6 Стационарный многошаговый градиентный метод.

В градиентном методе векторы строятся в виде xk+1 = xk k rk Тогда числа матрицы А.

В рассматриваемом методе используется оценка и мы приходим к задаче:

среди полиномов QN () = 1 + C1 + C2 2 +. + CN N найти полином, такой что Такой полином существует и единственен, и мы его построим в следующем параграфе.

Рассмотрим функции n (x) = cos(n arccos x), заданные на отрезке [1, 1] n = 0, 1, 2. Ясно, что |n (x)| 1. При n = 0 0 (x) = 1, при n = 1 1 (x) = x.

Мы получаем реккурентные формулы для вычисления значений функций n (x) :

2 (x) = 2x · x 1 = 2×2 1 — четная функция, 3 (x) = 2x(2×2 1) x = 4×3 3x — нечетная функция и т.д.

Таким образом, значения функций n (x) могут быть продолжены и для |x| 1. Тогда n (x)- полином степени n с коэффициентом при xn, равным 2n1 : n (x) = 2n1 xn +.

Определение. Полиномы Tn (x) = 2n1 n (x) называются полиномами Чебышева.

Ясно, что Tn (x) = 1 · xn + an1 xn1 +. + a0, и при x [1, 1] значения |Tn (x)| 2n1.

Нули полинома Чебышева.

Для |x| 1 получаем cos(n arccos x) = 0, n arccos x = 2k+1, На отрезке [1, 1] получаем n различных нулей полинома Чебышева. В точке x = 1 значение Tn (1) = 2n1, а Tn (1) = (1) 2n1. Вне отрезка [1, 1] нулей полинома Tn (x) нет.

Стационарные точки полинома Чебышева.

лучаем (n 1) стационарных точек x = cos k, k = 1, 2. (n 1), принадлежащих интервалу (1, 1).

При |x| 1 функции Tn (x) монотонные функции. Стационарные точки x располагаются между нуk лями полинома Tn (x). Значения |Tn (x)| в точках 1, x. x, 1 равны 2n1, а при |x| 1 значения |Tn (x)| 2n1. Значения Tn (x) в этих точках последовательно меняют свой знак. В этом случае говорят, что точки 1, x. x, 1- точки чебышевского альтернанса функции Tn (x).

Основное свойство полиномов Чебышева на отрезке [1, 1].

Пусть Qn (x)- любой полином степени n вида Qn (x) = 1 · xn + cn1 xn1 +. + c0.

Теорема. Для любого полинома Qn (x), отличного от Tn (x) при |x| 1, верно неравенство Доказательство. Предположим, что max |Qn (x)| max |Tn (x)| = 2n1.

Образуем полином Rn1 (x) = Tn (x) Qn (x) степени (n 1).

Рассмотрим сначала случай, когда в точках x значения Qn (x ) = Tn (x ), k = 1, 2. (n 1). На отрезке [x1, 1] полином Rn1 имеет не менее одного нуля, на отрезке [x, x ] полином Rn1 имеет не менее одного нуля и на каждом отрезке [x, x ], k = 2, 3. (n 1), а также на отрезке [1, x ] полином имеет не менее одного нуля. Тогда на всем отрезке [1, 1] полином Rn1 (x) имеет не менее n нулей, что возможно только если Rn1 (x) 0 на (, ).

Если же в некоторой точке x Tn (x ) = Qn (x ), то в этой точке Qn (x ) = Tn (x ) и x есть ноль, порядок которого не меньше двух. С учетом кратности полином Rn1 имеет на отрезке [1, 1] не менее n нулей и поэтому Tn (x) = Qn (x).

Полином Чебышева — полином наименее отклоняющийся от нуля на отрезке [1, 1] среди всех полиномов вида xn + cn1 xn1 +. + c0.

Построим полином n () степени n наименее отклоняющийся от нуля на отрезке [a, b] среди всех полиномов вида 1 + c1 + c2 2 +. + cn n, предполагая что a 0. Линейное преобразование отображает отрезок a b на отрезок [1, 1]. Полином наименее отклоняющийся от нуля на отрезке [a, b] равен При = 0 его значение равно Tn ( ba ). Требуемый полином n () равен Нули этого полинома Заметим, что ba 1 и значение Tn ( ba ) следует вычислять, исходя из полиномиального представления полинома Чебышева.

4.8 Многошаговый стационарный градиентный метод Поставленная в конце §6 задача имеет единственное решение:

При реализации метода достаточно знать только нули 0 этого полинома:

Обозначим Построим последовательность векторов xk+i :

Ясно, что порядок перечисления шагов при построении xk+N безразличен. Для N (A) 2 верна оценка Найдя xN +k повторяет цикл, возможно с другим набором шагов, изменяя степень полинома Чебышева.

Заключение. Кроме методов решения СЛАУ и минимизации значений квадратичной функции существуют и другие методы (метод вращений, метод покоординатного спуска и др.) Для минимизации значений произвольных (дифференцируемых) функций многих переменных применяется метод последовательной линеаризации в окрестности точек xk с последующей минимизацией значений получаемых квадратичных функций.

Видео:Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

ИНТЕРПОЛИРОВАНИЕ ФУНКЦИЙ.

ВВЕДЕНИЕ. Общая постановка задачи.

Рассматривается линейное метрическое пространство F. В этом пространстве выбрано (n+1) линейно независимых («базисных») элементов 0, 1. n и задано (m+1) функционалов J0, J1. Jm.

Задача. Для любого элемента f F требуется построить линейную комбинацию f элементов n такую что Ji (f ) = Ji (f ), i = 0, 1. m.

В общем случае элементы f и f не совпадают. Но мы не можем их различить, зная только (m+1) значений функционалов J0, J1. Jm на этих элементах. Как правило построение элемента f не является ших операций. Поэтому для оценки точных результатов необходимо уметь оценивать близость элементов f и f, т.е. оценивать расстояние (f, f ) в метрике пространства F.

Поставленная задача является классической задачей вычислительной математики, она изучалась многими учеными, начиная с И.Ньютона (1711г.) и Ж.Лагранжа (1806г.). Существует множество учебников и учебных пособий по этой тематике, среди них отметим:

-Н.Бахвалов, Н.Жидков, Г.Кобельков. Численные методы. 2003г.

-В.Вержбицкий. Основы численных методов. 2002г.

В этих учебниках приведена обширная библиография.

5.1 Интерполирование функций алгебраическими полиномами.

В качестве пространства F задается пространство [a, b] функций заданных и непрерывных на отрезке [a, b]:

«Базисными»элементами выбраны функции На отрезке [a,b] заданы различные точки xi (узлы), а в качестве функционалов Ji (f ) рассматриваются функционалы Линейные комбинации «базисных»элементов-полиномы степени n, рассматриваемые на [a,b].

Задача. Для заданной непрерывной на [a,b] функции f(x) построить полином fn (x) степени n такой что во всех узлах xi Решение этой задачи легко получить: достаточно решить систему линейных алгебраических уравнений относительно неизвестных значений C0, C1. Cn :

Матрица этой системы и её определитель — определитель Вандермонда-отличен от нуля. По формулам Крамера где Aik -алгебраические дополнения элементов k-того столбца определителя. Тогда Обозначив li (x) = Полиномы n-ой степени li (x) зависят только от выбора узлов x0. xn. Полином fn (x) называется интерполяционным полиномом для функции f (x) с узлами x0. xn 5.2 Интерполяционный полином в форме Лагранжа.

Значение полиномов li содержит вычисление определителей порядка (n + 1). Так как эти определители имеют специальный вид, то их вычисление несложно. Лагранж предложил метод, позволяющий получить полиномы li без непосредственного вычисления определителей. Равенства f (xj ) = fn (xj ) = f (xi )li (xj ) будут выполнены, если потребовать, чтобы Единственным полиномом степени n, обладающим этим свойством, является полином Компактную запись полинома li (x) можно получить, если ввести обозначение n+1 (x) = (xi x0 )(xi x1 ). (x( i)xi1 )(xi xi+1 ). (xi xn ). Ясно, что производная функции n+1 в точке x = xi равна n+1 (xi ) = (xi x0 )(xi x1 ). (x( i)xi1 )(xi xi+1 ). (xi xn ), и тогда li (x) = 1(xi ) n+1 (x) Полученная таким образом форма интерполяционного полинома обозначается Ln (f, x):

и называется интерполяционным полиномом в форме Лагранжа. Отметим три свойства интерполяционных полиномов, не зависящих от конкретной формы интерполяционного полинома:

1. Интерполяционный полином не зависит от порядка перечисления узлов.

j= достаточно заметить, что коэффициенты полиномов li (x) при xn равны 1. Особенностью представления интерполяционного полинома в форме Лагранжа является возможность быстрого построения интерполяционного полинома для любой функции f F при фиксированном наборе узлов, если полиномы li (x) уже найдены. Однако при добавлении нового узла придется заново строить полиномы li (x).

Ньютон построил интерполяционный полином, пользуясь введенным им понятием разделенных разностей. В методике Ньютона введение нового узла сводится к вычислению лишь одного дополнительного слагаемого.

разностями первого порядка. Они обозначаются Далее вводятся разделенные разности второго порядка И разделенные разности k-го порядка В частности разделенная разность порядка k:

и эта величина не зависит от порядка перечисления узлов. Проведя элементарные выкладки, легко показать (по индукции), что разделенные разности k-го порядка равны и их значения не зависят от порядка перечисления узлов в наборе x0, x1. xk. Согласно свойству 3) коэффициент ak при xk в интерполяционном полиноме fk (x) равен 5.4 Интерполяционный полином в форме Ньютона.

Пусть fk (x)-интерполяционный полином для функции f (x), построенный по узлам x0, x1. xk1. Тогда разность fk (x) fk1 (x)-полином степени k, обращающийся в ноль в точках x0, x1. xk1. Ясно, что где a равен коэффициенту полинома fk (x) при xk :

Интерполяционнай полином для функции f (x), построенный по одному узлу x0 равен Поэтому естественно определить разделенную разность нулевого порядка как f (x0 ), а значение 0 (x) 1.

Ясно что Такая форма представления интерполяционного полинома fn (x) обозначается Nn (f, x) и говорят, что интерполяционный полином представлен в форме Ньютона:

При введении нового узла xn+ Для вычисления дополнительного слагаемого приходится последовательно вычислять разделенные разности Обозначим rn (f, x) = f (x) fn (x) и оценим для заданной функции f (x) и для фиксированного набора узлов x0, x1. xn. Для краткости будем обозначать rn (x) = rn (f, x). Ясно, что без дополнительных ограничений на функцию f (x) невозможно получить оценку величины rn (x). Будем предполагать, что функция f (x) имеет на [a,b] непрерывную производную порядка (n+1) и известна оценка:

Пусть x -произвольная точка отрезка [a,b]. Оценим rn (x ). Ясно, что если x совпадает с одним из узлов xi, то rn (x) = 0. Поэтому будем рассматривать точку x не совпадающую ни с одним из узлов. Построим вспомогательную функцию (x):

Эта функция имеет непрерывные производные до порядка (n+1) включительно. В точках x0, x1. xn и в точке x функция (x) обращается в ноль. Таким образом, эта функция имеет на [a,b] не меньше (n+2) нулей. Тогда производная (x) имеет не менее (n+1) нулей и n+1 (x) имеет на [a,b] по крайней мере один ноль. Следовательно существует точка [a, b], в которой n+1 () = 0. Так как то в точке значение f n+1 () = rn (x ) ) (n + 1)!. Таким образом для любого значения x [a, b] существует точка (зависящая от x), такая что и мы получаем оценку Эту оценку нельзя улучшить:взяв функцию f (x):

для которой f (n+1) (x) = Mn+1, мы получим Рассмотрим постановку задачи интерполирования, в которой узлы x0, x1. xn не фиксированы и их можно выбирать для улучшения оценки методической погрешности. Исходя из оценки (2) будем выбирать узлы xi из условия Так как n+1 (x) — полином степени (n+1) и n+1 (x) = (xx0 )(xx1 ). (xxn ) = 1·xn+1 +an xn +. +a1 x+a0, то оптимальный полином — полином, наименее отклоняющийся от нуля на отрезке [a, b]. Если [a, b] = [1, 1], то n+1 (x)-полином Чебышева Tn+1 (x), нулями которого являются числа xi, равные Для построения полинома n+1 (x) выберем узлы xi — нули полинома наименее отклоняющегося от нуля на отрезке [a, b]:

Согласно оценке значений полинома, наименее отклоняющегося от нуля, получаем и затем оценку 5.7 Разделенные разности и производные функции.

К набору узлов x0, x1. xn добавим еще один узел x [a, b]. Тогда и в точке x = x Так как x — произвольная точка отличная от xi, то получаем тождество верное и для всех значений x [a, b].

Согласно равенству (1) В частности где [a, b].

5.8 Численное дифференцирование. Методическая погрешность Построив интерполяционный полином, легко находить приближенные значения интегралов и производных исходной функции f (x). В этом параграфе мы оценим точность приближения производных f (m) (x) при замене функции f (x) интерполяционным полиномом в предположении, что функция f имеет [a, b] непрерывные производные до порядка n + m + 1 включительно. При этом мы будем представлять интерполяционный полином в форме Ньютона. Ясно что m должно быть не больше n : m n.

Представим rn (x) в виде rn (x) = f (x0, x1. xn, x)n+1 (x). Ясно что f (x0, x1. xn, x) имеет столько же непрерывных производных сколько и функция f (x).

Мы получим оценку rn,m (f, x), если сумеем оценить производные разделенных разностей Для этого рассмотрим произвольную функцию g(x) Ck [a, b] и её разделенную разность g(x, x + h, x + 2h. x + kh) порядка k. Согласно (3) её можно представить в виде где лежит между точками x и x + kh. Тогда при h Рассмотрим в качестве g(x) функцию g(x) = f (x0, x1. xn, x) — разделенную разность порядка (n + 1) функции f (x).

Но f (x0, x1. xn, x, x + h, x + 2h. x + kh) = (n+k+1)! f (n+k+1) (h ), где h [a, b]. Рассмотрим последовательность h 0 и последовательность h. Последовательность h можно и не иметь предела, но так как она ограничена, то из неё можно выбрать последовательность, сходящуюся к некоторой точке [a, b].

Для этой подпоследовательности существует предел Значение зависит от точки x. Таким образом получаем оценку и оценку Замечание: Для равностоящих узлов xi, x0 = a, xn = b можно получить оценку rn,m (f, x) для функций f Cn+m [a, b].

Пример: Узлы x0 и x1, n=1, m= f C2 [x0, x1 ].

С другой стороны непосредственно получаем 5.9 Полная погрешность численного дифференцирования.

Как правило значение функции f или вследствие погрешности их вычисления или вследствие их измерений известны с некоторой точностью, т.е. известны значения f (x) = f (x) + (x), где (x) — погрешность задания функции f (x).

Тогда полная погрешность интерполирования равна сумме методической погрешности и неустранимой погрешности.

В этом параграфе мы оценим полную погрешность численного дифференцирования. Предполагая что функция f Cn+2 [a, b], получим Относительно функции (x) мы можем предполагать только её ограниченность |(x)|.

и полная погрешность оценивается величиной:

Остановимся на одном частном случае.

Рассмотрим два узла x0 и x1 = x0 + h и функцию f C2 [x0, x1 ]. Методическая погрешность численного дифференцирования оценивается |r1,1 (f, x)| M2 h, а так как Полная погрешность численного дифференцирования оценивается величиной M2 h + 2.h Если величину h можно выбирать, то её следует выбирать так, что значение M2 h + 2 было бы миниh мальным. Ясно, что минимум достигается при При таком выборе h полная погрешность численного дифференцирования не превосходят 2 2M2.

Уменьшая, например, погрешность задания функции f (x) в 100 раз мы получим уменьшение полной погрешности численного дифференцирования всего в 10 раз при одновременном уменьшении шага в раз.

Рассматриваются узлы a = x0, xi = x0 + ih, xn = x0 + nh = b и значения fi = f (xi ) непрерывной на [a, b] функции f (x). Определим конечные разности k fi k-того порядка:

Нас будут интересовать конечные разности k f0 :

и их связь с разделенными разностями f (x0, x1. xk ) порядка k.

Ясно, что f (x0, x1 ) = hfo. Легко показать, что верна формула Действительно, пусть она верна при некотором значении k(k = 1). Тогда Из (4) следует, что интерполяционный полином fn (x) можно представить в виде:

положив 0 fk = f (xk ).

В заключении отметим, что rn (f, x) = f (x) fn (x) = (n+1)! f (n+1) ()n+1 (x), и для функции f (x) = Cn+1 x Таким образом для оценки rn (f, x) следует оценить |n+1 (x)|.

Из последнего представления интерполяционного полинома можно получить интересное свойство fn (x). Пусть в процессе вычислений получены значения k f0, k = 0, 1. n. Оценим вклад k-того слагаемого в значении fn для x [x0, x1 ]. Коэффициент при k f0 равен (x = x0 + th, t [0, 1]):

При малых t величина |k (x)| t(1 t) k. Таким образом, вычислив значения k f0 можно судить о влиянии k-того слагаемого в интерполяционной формуле на значения интерполяционного полинома для x [a, a + h]. Это влияние убывает с ростом k достаточно медленно. Немецкий математик Рунге около 1900 г. рассмотрел на отрезке [1, 1] бесконечно дифференцируемую функцию и показал, что интерполяционный полином fn (x), построенный по равноотстоящим узлам, не стремится с ростом n к этой функции:

при n. Завершая этот параграф, отметим, что можно строить интерполяционный полином, взяв в качестве начальной точки значение x = b и шаг h. Можно взять в качестве x0 середину отрезка [a, b] и одновременно брать узлы x0 + kh, x0kh. Эти и другие возможности приведены в книге В.М.Вержбицкого «Основы численных методов».

5.11 Интерполирование с кратными узлами (интерполяционный Далее мы рассмотрим другие постановки задач интерполирования. Пусть в узлах x0, x1. xn помимо значений f (xi ) известны (вычислены,измерены) значения производных функции f (x):

Обозначим N = max<m>. Для каждого узла xi рассматриваются все производные до порядка mi включительно. Число всех величин в узлах равно Требуется построить полином, удовлетворяющий всем поставленным условиям. Такой полином должен иметь степень m и этот полином, если он существует, определяется единственным образом. Действительно, если разность двух таким полиномов Pm (x) Qm (x) = Rm (x) не равна тождественно нулю, то степень полинома Rm не превосходит m. Но узлы xi являются его нулями кратности mi :

Стало быть степень полинома Rm (x) равна m + 1, что невозможно.

Для искомого полинома можно построить систему линейных алгебраических уравнений относительно его неизвестных коэффициентов. Она имеет единственное решение. Таким образом поставленная задача имеет решение и это решение единственно.

Полином, удовлетворяющий условиям задачи, называется интерполяционным полиномом Эрмита и обозначается Hm (f, x).

Укажем «наивный»способ построения полинома Hm (x). В непересекающихся h- окрестностях каждого узла xi выберем mi дополнительных точек xi,1, xi,2. xi,mi. Вычислим значения в этих точках, используя формулу Тейлора для функции f (x) с известными значениями f (xi ), f (xi ). f (mi ) (xi ).

Вместе с узлами x0, x1. xn мы получим ещё m0 +m1 +. +mn узлов, в которых значения функции f (x) известны приближенно. Построим интерполяционный полином Lm (f, h; x) по этим узлам. Тогда, устремив h к нулю, получим Ясно, что такой метод неконструктивен. Но он позволяет получить представление rm (f, x) = f (x) Hm (f, x):

5.12 Метод построения интерполяционного полинома Эрмита.

Укажем один из возможных методов построения полинома Hm (f, x).

1. По значениям функции f (x) в узлах x0, x1. xn построим интерполяционный полином L(f, x).

2. Представим разность f (x) L(f, x) в виде Функция F1 (x) неизвестна. Однако её значения и значения всех производных, участвующих в таблице, можно вычислить. Действительно В тех узлах, где заданы значения вторых производных, получаем значения F1 (xi ):

Продолжая дифференцирование функции f (x) L(f, x), получаем значения функции F1 (x) и всех её производных в узлах, входящих в таблицу.

Таким образом для функции F1 (x) получаем задачу кратного интерполирования. Ясно что 3. Построим интерполяционный полином L(F1, x) по значениям F1 (x) в узлах и представим разность F1 (x) L(F1, x) в виде Тогда Аналогично пункту (2) получим задачу кратного интерполирования для функции F2 (x).

4. Продолжая этот процесс, получим задачу кратного интерполирования для функции FN 1 (x), построим интерполяционный полином L(FN 1, x) и разность FN 1 (x) L(FN 1, x) представим в виде Для функции FN (x) получим только её значение в узлах исходной таблицы, в которых заданы значения производных f (x) наибольшего порядка N. По значениям FN (x) в этих узлах построим интерполяционный полином L(FN, x) и FN (x) = L(FN, x) + r(FN, x) Окончательно получаем Пренебрегая величиной r(FN, x), получим интерполяционный полином Эрмита:

Представление f (x) Hm (f, x) можно получить, минуя представление r(FN, x). Согласно (5):

Замечание: Если значение функции f и всех её производных до порядка n включительно заданы только в одном узле, то Пример.

Построить интерполяционный полином Эрмита H5 (f, x), удовлетворяющий этой таблице значений.

1. По значениям f (x) в узлах -1,0,1 построим интерполяционный полином L(f, x) : L(f, x) = 1 + x.

2. Разность f (x) L(f, x) представим в виде f (x) L(f, x) = (1, x)F1 (x), где (1, x) = (x x0 )(x x1 )(x x2 ) = x3 x, F1 (x)-неизвестная функция.

f (x) = 1 + x + (x3 x)F1 (x). Производная f (x) = 1 + (3×2 1)F1 (x) + F1 (x). В узлах, где заданы значения f (x), получаем Вторая производная функции f (x):

Значение f (x) известно только в одном узле x0 = 1:

Таким образом для функции F1 (x0 ) получаем таблицу значений:

3. Для функции F1 (x) построим интерполяционный полином по её значениям в узлах x0, x1 : L(F1, x) = 1 x и представим разность F1 (x) L(F1 , x) в виде F1 (x) L(F1, x) = (2, x)F2 (x) и где (2, x) = (x + 1)x, F2 (x)-неизвестная функция.

Производная функции F1 (x) равна и в узле x 4. Для функции F2 (x) строим интерполяционный полином по её значению с точке x0 : L(F2, x) = 1 и Если F2 (x) дифференцируемая функция, то r(F2, x) = F2 ()(x x0 ). Итак f (x) = 1 + x + (1, x)(1 x + (x + 1)x(1 + r(F2, x))) = 1 + x + (x3 x)(1 x + x2 + x + x(x + 1)r(F2, x)) = Пренебрегая величиной r(F2, x), получаем Согласно (5) если f C6 [x0, x2 ].

Рассмотрим последовательность разбиений n отрезка [a,b] узлами x1, x2. xn, требуя чтобы с ростом n диаметр разбиения стремился к нулю.

Для функции f (x) построим последовательность интерполяционных полиномов Ln (n, f ; x). Разбиение n задает интерполяционный процесс (n, f ) для функции f. Обозначим r(n, f ; x) = f (x) Ln (n, f ; x).

Говорят, что интерполяционный процесс (n, f ) сходится в точке x [a, b], если lim r(n, f ; x ) = при n.

Говорят, что интерполяционный процесс сходится равномерно на [a, b], если max |r(n, f ; x)| 0 при Теорема Марцинкевича.

Для каждой непрерывной функции f (x) существует такой интерполяционный процесс, что r(n, f ; x) 0. В этой теореме n = n (f ).

Для любой последовательности разбиений n отрезка [a, b] существует непрерывная функция f (x), такая что max |r(n, f ; x)| не стремится к нулю при n.

В этой теореме f = f (n ).

Для отрезка [1, 1] при разбиении разноотстоящими узлами пример такой функции привел Рунге:

Для функции f (x) = |x| для такого же разбиения отрезка [1, 1] Бернштейн показал, что lim r(n, f ; x) = 0 только в точках x = 1, x = 0, x = 1.

Рассмотренные постановки задач интерполирования имеют существенные недостатки:

-увеличение степени полиномов при увеличении числа узлов.

-величина rn (f, x) = f (x) fn (x) оценивается через значения производной функции f порядка (n + 1) в предположении, что f Cn+1 [a, b].

-увеличение числа узлов не гарантирует в общем случае уменьшения max |rn (f, x)|.

В следующий параграфах мы рассмотрим другую постановку задач интерполирования алгебраическими полиномами.

5.14 Сплайны класса Sn,k. (Кусочно-полиномиальное Пусть задана возрастающая последовательность узлов Функция S(x) Ck [x0, xN ] называется сплайном класса Sn,k, если на каждом отрезке между узлами она является полиномом степени не выше n.

Если k = n, то Sn,n -множество степени не выше n, заданных на [x0. xN ]. Величина =n k называется дефектом сплайна.

Для фиксированной последовательности узлов xi множество функций класса Sn,k является линейным подпространством пространства Ck [x0, xN ]. Покажем, что это подпространство конечномерно, построив базис в классе Sn,k.

Ясно, что эти базисные функции i,j (x) линейно независимы. Назовем их исходными базисными функциями класса Sn,k.

В каждом внутреннем узле xi значения i,j (x), i,j (x). k (x) равны нулю, поэтому линейные комбиi,j нации этих базисных функций являются сплайнами класса Sn,k. С другой стороны каждый сплайн этого класса можно представить в виде линейной комбинации исходных базисных функций.

Введем сквозную нумерацию исходных базисных функций:

Постановка задачи интерполяции. Для функции f C[x0, xN ] построить сплайн S(x) класса Sn,k, такой что S(xi ) = f (xi ), i = 0, 1. N.

Представляя искомый сплайн в виде S(x) = Cj, j, приходим к задаче определения коэффициентов Таким образом задача интерполяции кусочно-полиномиальными функциями является частным случаем задачи интерполирования. В общем случае число условий N + 1 меньше и коэффициенты Cj определяются неоднозначно. Решение поставленной задачи можно упростить, если рассмотреть новый базис si (x), i = 0, 1. N, где каждая функция si (x) является линейной комбинацией исходных базисных функций.

Например, для класса S1,0 такими линейными комбинациями являются сплайны класса S1,0, построенные по узлам xi1, xi, xi+1, равные нулю при x xi1 и при x xi+1, а в узле xi значение si (xi ) = 1.

5.15 Построение интерполяционного сплайна класса S3,2.

По сравнению со сплайнами классов S3,0 и S3,1 сплайны класса S3,2 имеют наибольшую гладкость.

Необходимость построения интерполяционных сплайнов класса S3,2 возникает при решении многих практических задач. Например, при изготовлении стальных шпангоутов (балок) судов заданы только координаты точек (xi, f (xi )), через которые должен проходить профиль шпангоута. Прочность судна зависит от потенциальной энергии напряжений, возникающий при изгибе балки. Потенциальная энергия P (S) профиля y = S(x) пропорциональна интегралу Естественно возникает задача минимизации P (S) при условиях S(xi ) = f (xi ) и условиях непрерывности S(x), S (x), S (x). Эта задача-классическая задача вариационного исчисления. Оптимальная функция S(x) должна удовлетворять уравнению Эйлера и граничным условиям S (x0 ) = 0, S (xN ) = 0. Следовательно S(x) является полиномом степени 3 на каждом отрезке [xi1, xi ], а на всем отрезке [x0, xN ]-сплайн класса S3,2 с дополнительными граничными условиями. Обозначим Si (x) значения сплайна S(x) при x [xi, xi+1 ], а через hi обозначим длину отрезка [xi, xi+1 ], hi = xi+1 xi. Так как Si (xi ) = f (xi ), то где коэффициенты bi, Ci, di подлежат определению.

1. Условие непрерывности S(x) во внутренних точках xi :

Условие SN 1 (xN ) = fN приводит к уравнению:

Полученные уравнения можно записать в виде:

2. Условие непрерывности S (x) во внутренних узлах xi :

или 3. Условие непрерывности S (x) во внутренних узлах xi :

или Таким образом для 3N неизвестных коэффициентов мы получили N + 2(N 1) = 3N 2 уравнений.

В теории упругости для балки с фиксированными торцами условия равновесия имеют вид где µ характеризует упругие свойства внешней среды. Эти два соотношения дают необходимые условия для разрешимости системы линейных уравнений.

В случае, если к торцам балки не приложены силы, то коэффициент µ = 0 и для граничных точек получаем: S (x0 ), т.е. C0 = 0 и S (xN ) = 0, т.е. SN 1 (xN ) = 0, CN 1 + dN 1 hN 1 = 0. Таким образом получаем два недостающих условия:

Последнее условие можно включить в условия (С) при i = N, положив формально CN = 0 : dN 1 = CN CN Метод решения полученной системы состоит в последовательном исключении неизвестных di, затем bi.

В результате мы получим систему линейных уравнений для определения коэффициентов Ci.

Из (А) исключаем bi :

и подставляя в условия (В), получаем уравнение для Ci :

Умножая эти уравнения на 6, получаем систему линейных алгебраических уравнений с матрицей размерности (N 1) (N 1):

и с вектор-столбцом правой части:

Эта матрица трёхдиагональная с диагональным преобладанием. Решение системы уравнений можно получить методом прогонки, прогоночные коэффициенты по модулю меньше 1, метод устойчив. Для других граничных условий изменяются первое и последнее уравнения, и присоединяются еще два уравнения при Для этих оценок рассмотрим равномерную сетку узлов: hi = h. Система уравнений для коэффициентов Ci имеет вид:

Будем предполагать, что f C 3 [x0, xN ]. Обозначим r(x) = S(f, x) f (x). Ясно, что Оценим последовательно величины |r (xi )|, |r (x)|, |r (x)| и |r(x)|.

«ЦЕНТРОСОЮЗ РОССИЙСКОЙ ФЕДЕРАЦИИ СИБИРСКИЙ УНИВЕРСИТЕТ ПОТРЕБИТЕЛЬСКОЙ КООПЕРАЦИИ БУХГАЛТЕРСКИЙ УЧЕТ В ПРЕДПРИЯТИЯХ ПОТРЕБИТЕЛЬСКОЙ КООПЕРАЦИИ Методические указания, программа и задания контрольной и самостоятельной работы для студентов заочной формы обучения специальности 060500 (080109) Бухгалтерский учет, анализ и аудит Новосибирск 2005 Кафедра бухгалтерского учета Бухгалтерский учет в предприятиях потребительской кооперации: Методические указания и задания / Сост. доц. О.П. Николаева, доц. »

«Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Амурский государственный университет Кафедра китаеведения УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ Учебная практика Основной образовательной программы по специальности 032301.65 Регионоведение специализация Китай Благовещенск 2012 УМКД разработан к. п. н., доцентом Стародубцевой Натальей Сергеевной Рассмотрен и рекомендован на заседании. »

«Федеральное агентство по образованию ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР) Кафедра автоматизированных систем управления (АСУ) А.В. Ковшов ТЕОРИЯ СИСТЕМ И СИСТЕМНЫЙ АНАЛИЗ Учебное методическое пособие 2009 Корректор: Осипова Е.А. Ковшов А.В. Теория систем и системный анализ: Учебное методическое пособие: Томский межвузовский центр дистанционного образования, 2009. — 45 с. Учебно-методическое пособие предназначено для получения практических навыков. »

«База нормативной документации: www.complexdoc.ru ГОСУДАРСТВЕННЫЙ КОМИТЕТ СССР ПО НАРОДНОМУ ОБРАЗОВАНИЮ МОСКОВСКИЙ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ АВТОМОБИЛЬНО-ДОРОЖНЫЙ ИНСТИТУТ М.В. Немчинов ПРОЕКТИРОВАНИЕ ВОДОСТОКА В ГОРОДАХ Учебное пособие Утверждено в качестве учебного пособия редсоветом МАДИ МОСКВА СОДЕРЖАНИЕ СОДЕРЖАНИЕ ВВЕДЕНИЕ База нормативной документации: www.complexdoc.ru 1. ОРГАНИЗАЦИЯ СТОКА ПОВЕРХНОСТНЫХ ВОД 2. ПРОЕКТИРОВАНИЕ ВОДОСТОЧНОЙ СЕТИ. »

«МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ КОНТРОЛИРУЕМОЙ САМОСТОЯТЕЛЬНОЙ РАБОТЫ ПО КУРСУ СТАТИСТИКА ПРЕДПРИЯТИЙ ОТРАСЛИ Введение В современной методике преподавания в ВУЗе самостоятельная контролируемая работа является неотъемлемой частью изучения дисциплины без непосредственного участия преподавателя, но под его руководством, контролем и по предлагаемым заданиям. Самостоятельная контролируемая работа позволяет дополнить и расширить получаемые студентами знания в процессе аудиторной работы. Данный. »

«МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ – УЧЕБНО-НАУЧНОПРОИЗВОДСТВЕННЫЙ КОМПЛЕКС ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ ИМЕНИ Н.Н.ПОЛИКАРПОВА ФАКУЛЬТЕТ СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Методические указания по преддипломной практике для специальности 230105 Программное обеспечение вычислительной техники и автоматизированных систем Орел — 2012 2 ОДОБРЕНО. »

«Министерство образования и науки Российской Федерации Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Амурский государственный университет Кафедра Информационных и управляющих систем УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ДИСЦИПЛИНЫ БАЗЫ ЗНАНИЙ И ЭКСПЕРТНЫЕ СИСТЕМЫ Основной образовательной программы по специальности 230102.65 – Автоматизированные системы обработки информации и управления Благовещенск 2012 УМКД разработан доцентом Акиловой Ириной. »

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЛЕСНОГО ХОЗЯЙСТВА **** УЧЕБНО-МЕТОДИЧЕСКИЙ И ОБРАЗОВАТЕЛЬНЫЙ ЦЕНТР ПАРТНЕР МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ по администрированию платежей за пользование лесным фондом, поступающих в бюджетную систему Российской Федерации Москва, 2005 Настоящие Методические рекомендации разработаны Учебнометодическим и образовательным центром ПАРТНЕР по заданию Федерального агентства лесного хозяйства в помощь работникам территориальных органов Рослесхоза, лесхозов и лесничеств в целях организации. »

«ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ Факультет дизайна и технологии Кафедра конструирования и технологии одежды ИЗГОТОВЛЕНИЕ ТРИКОТАЖНЫХ ИЗДЕЛИЙ НА ПЛОСКОВЯЗАЛЬНОМ ОБОРУДОВАНИИ С ПОМОЩЬЮ ПРОГРАММЫ АВТОМАТИЗИРОВАННОГО ПРОЕКТИРОВАНИЯ ОДЕЖДЫ DESIGN KNIT 7 (по дисциплинам Основы ресурсосберегающих технологий и Конструирование трикотажных изделий) Учебно-методическое пособие. »

«ЦКП Материаловедение и диагностика в передовых Оглавление: технологиях при ФТИ им. А.Ф. Иоффе Происхождение рентгеновского излучения 3 Физические основы рентгеновской дифрактометрии 4 Физические основы рентгеновской рефлектометрии 5 Оборудование для проведения измерений 6 Возможности XRD и XRR 9 Получение рентгеновских кривых 10 Определение толщины и состава эпитаксиального слоя 11 Рентгеновская дифрактометрия структур со сверхрешетками ВЫСОКОРАЗРЕШАЮЩАЯ РЕНТГЕНОВСКАЯ Определение толщины слоя и. »

«ЗАОЧНАЯ ЕСТЕСТВЕННО-НАУЧНАЯ ШКОЛА ПРИ СИБИРСКОМ ФЕДЕРАЛЬНОМ УНИВЕРСИТЕТЕ МАТЕМАТИКА АДАПТАЦИОННЫЙ КУРС Учебное пособие Допущено УМО по классическому университетскому образованию в качестве учебного пособия по дисциплине вузовского компонента Математика. Адаптационный курс для студентов высших учебных заведений, обучающихся по специальности ВПО 010101 Математика, направлениям 010100 Математика, 010300 Математика. Компьютерные науки Красноярск ИПК СФУ 2009 УДК 51(075) ББК 22.1я73 K97. »

«2929 ОСНОВНЫЕ СВЕДЕНИЯ О РАБОТЕ С ГРАФИЧЕСКИМ РЕДАКТОРОМ КОМПАС-3D Методические указания для студентов всех специальностей Иваново 2010 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования Ивановская государственная текстильная академия (ИГТА) Кафедра инженерной графики ОСНОВНЫЕ СВЕДЕНИЯ О РАБОТЕ С ГРАФИЧЕСКИМ РЕДАКТОРОМ КОМПАС-3D Методические указания для студентов всех специальностей Иваново 2010 В методических указаниях. »

«Приведены научные методы в сфере исследования процессов, услуг и работ по удовлетворению потребностей покупателей в текстильных мате­ риалах и швейных изделиях. Практикум содержит основные теоретиче­ ские сведения по методам статистической обработки экспериментальных данных и планированию эксперимента, методические указания для про­ ведения лабораторных работ, приложения и перечень рекомендуемой ли­ тературы. Для студентов вузов и аспирантов специальности Сервис, а также Технология швейных. »

«МОДЕЛИРОВАНИЕ СИСТЕМ И ПРОЦЕССОВ МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ Состав курса • 36 лекций • 5 лабораторных работ (1-я, 2-я — на компьютерах, 3-я, 4-я — резервные, 5-я репетиция экзамена) • 4 практических занятия (1-е + 2-е сдвоенное — ознакомительное) • КДЗ — РГР (3 задачи по методичке) • Экзамен на компьютерах 1 Литература Математическое моделирование: 517.8 Учебное пособие. Ч. I и II. 2004. К88 Аэродинамика и динамика полета: 052–011 Учебное пособие. 2000. К88 методичка по изучению № 1233. »

«Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования Ивановская государственная текстильная академия (ИГТА) Кафедра материаловедения и товароведения МАТЕРИАЛЫ ДЛЯ ОДЕЖДЫ И КОНФЕКЦИОНИРОВАНИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ к выполнению контрольных работ для студентов специальности 260901 (280800) Технология швейных изделий заочной формы обучения Иваново 2009 Методические указания предназначены для студентов заочного факультета специальности. »

«Федеральное агентство по образованию Государственное образовательное учреждение высшего профессионального образования АМУРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГОУВПО АмГУ УТВЕРЖДАЮ Заведующий кафедрой _ Т.В. Кезина _ _ 2010г. УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС по дисциплине Промышленные типы месторождений полезных ископаемых для специальности 130301 (Геологическая съемка, поиски и разведка месторождений полезных ископаемых) Составитель: Авраменко С.М., ст.преподаватель кафедры ГиП Благовещенск 2010 г. »

«Министерство образования РФ Восточно-Сибирский государственный технологический университет Кафедра Технология изделий легкой промышленности Методические указания к выполнению лабораторных работ по курсу Материаловедение изделий из кожи часть 1 Составил: Минтаханова Т.М. Петрова Т.В. Улан-Удэ 1999 9. На лабораторных занятиях в соответствии с заданием и 1. Подготовка к выполнению лабораторной работы. дополнительными указаниями, полученными от преподавателя, студент Лабораторный практикум. »

«Фдоров Алексей Владимирович ОСНОВЫ УСТРОЙСТВА РАКЕТНО-КОСМИЧЕСКИХ КОМПЛЕКСОВ Учебное пособие 2012 2 СОДЕРЖАНИЕ ВВЕДЕНИЕ РАЗДЕЛ 1. ОСНОВЫ ПОСТРОЕНИЯ РАКЕТНО-КОСМИЧЕСКИХ КОМПЛЕКСОВ ОСНОВНЫЕ СВЕДЕНИЯ О КОСМИЧЕСКИХ СИСТЕМАХ. 1 СТРУКТУРА КОСМИЧЕСКОЙ СИСТЕМЫ И КОСМИЧЕСКОГО КОМПЛЕКСА 1.1 Структура космической системы 1.2 Космические системы связи 1.3 Космические навигационные системы 1.4 Космические метеорологические системы 1.5 Космические системы предупреждения о ракетном нападении. 1.6 Космические. »

«Раздел 8. РАСЧЕТ ТРЕХКОРПУСНОЙ ВЫПАРНОЙ УСТАНОВКИ С ЕСТЕСТВЕННОЙ ЦИРКУЛЯЦИЕЙ РАСТВОРА ВВЕДЕНИЕ В процессе выполнения курсового проекта студентам необходимо ознакомиться с методикой инженерного расчета технологического оборудования, его выбора и проектирования. Расчет задания на проектирование включает в себя технологический расчет выпарной установки и, как правило, прочностной и конструктивный расчеты отдельных аппаратов. Цель технологического расчета – определение количества выпаренной воды по. »

«МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ по дисциплине Грузоведение для студентов специальности Организация перевозок и управление на транспорте дневной и заочной ф о р м обучения Омск 2008 Федеральное агентство по образованию Сибирская государственная автомобильно-дорожная академия (СибАДИ) Кафедра организации перевозок и управления на транспорте МЕТОДИЧЕСКИЕ УКАЗАНИЯ ДЛЯ ПРАКТИЧЕСКИХ ЗАНЯТИЙ по дисциплине Грузоведение для студентов специальности Организация перевозок и управление на. »

© 2013 www.diss.seluk.ru — «Бесплатная электронная библиотека — Авторефераты, Диссертации, Монографии, Методички, учебные программы»

Материалы этого сайта размещены для ознакомления, все права принадлежат их авторам.
Если Вы не согласны с тем, что Ваш материал размещён на этом сайте, пожалуйста, напишите нам, мы в течении 1-2 рабочих дней удалим его.

Видео:Численные методы решения ДУ: метод ЭйлераСкачать

Лабораторная работа №2

Численные методы решения скалярных уравнений

Цель работы:сформировать у студентов представление о применении уравнений в различных областях деятельности, привить знания об основных этапах решения уравнения, выработать навыки использования различных методов для уточнения корня уравнения и выбора того или иного программного средства для проверки правильности найденного результата.

Метод хорд

Решить уравнение е х ∙ (2 – х) – 0,5 = 0 методом хорд с точностью ɛ = 0,001.

1. Отделяем корни.Этот этап решения осуществляется с помощью аналитического или графического метода. После того как корень, подлежащий уточнению, отделен, за начальное приближение может быть выбрана любая точка [a,b] (начало отрезка, его середина и т.д.).

Воспользуемся графическим методом. Построим график функций и найдем точки пересечения его с осью Ох (рис.2.1.).

f(x) = (2 – x) (e x ) – 0,5

Рис.2.1. Отделение корней графически

Получили два интервала: [-3; -2], [1,5; 2,5]. Интервал, в котором мы будем уточнять корень – [1,5; 2,5].

2. Уточняем корни. Находим первую производную функции

3. Определяем знакиf(x) на отрезке [1,5; 2,5]:

f(1,5) = 1,741>0, f(2,5) = -6,591 8,801∙ 10 -4 ), значит х₈ = 1,927 является решением нашего уравнения.

п = 0. 10

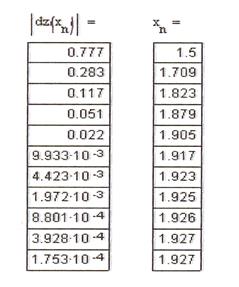
х₀=а

Рис. 2.2. Проверка критерия достижения

5. Создаем функцию, реализующую вычисления корня уравнения

е х ∙ (2 – х) – 0,5 = 0 на отрезке [1,5; 2,5] с точностью ɛ = 0,001 методом хорд (рис. 2.3). Решением будет являться число 1,927, получившееся на третьем шаге решении

Рис.2.3. Функция, возвращающая значения корня уравнения методом хорд.

Аргументы функции: а, b – концы отрезка; 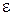– погрешность вычислений,

f 1pr(x) – функция первой производной

6. Проверяем решение уравнения встроенными функциями Матhcad

хl = root(f(x),x) xl = 1,927

(2 – x)∙(e X ) – 0,5 = 0

x2 = Find(x) x2 = 1,927

Метод касательных

Пример 2.2.

Вычислить методом касательных корень уравнения е х ∙(2 – х) –0,5=0 на отрезке[1,5; 2,5] с точностью ɛ = 0,001.

Решение.

1. Отделяем корни уравнения (см. разд. 2.1).

2. Определяем неподвижную точку.

Для этого определим знаки функции и второй производной на отделенном интервале [1,5; 2,5]. Для этого составим функцию, проверяющую условие неподвижности точки

f(x) = (2 – x)(e x ) – 0,5

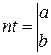
Тогда подвижной точкой будет точка а = 1,5.

3. Вычисляем значение итерационной последовательности с использованием рекуррентной формулы метода касательных (рис. 2.4).

х₀ = а

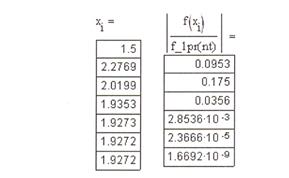
Рис. 2.4.Построение итерационной последовательности

по методу касательных

Анализируя полученные значения для достижения критерия заданной точности, можно сказать, что решением уравнения будет значение

х₄ = 1,927 при п = 4, т.к. 2,367∙10 -5 ˂ 0,001.

4. Создаем функцию, реализующую метод касательных (аналогично методу хорд).

5. Проверяем полученные результаты.

Отметим, что в пакете Mathcad имеется еще несколько функций, позволяющих решать уравнения, например, функция solve, вызываемая с панели Symbolic (рис. 2.5.)

Рис. 2.5. Панель Symbolic

Пример использования команды solve представлен на рис. 2.6.

Рис.2.6. Решение уравнения с помощью команды solve

Дата добавления: 2021-09-07 ; просмотров: 76 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

🎬 Видео

Алгоритмы. Нахождение корней уравнения методом хордСкачать

1,2 Решение нелинейных уравнений методом хордСкачать

14 Метод половинного деления Ручной счет Численные методы решения нелинейного уравненияСкачать