Введение
Наиболее распространённым уравнением эллиптического типа является уравнение Пуассона.
К решению этого уравнения сводятся многие задачи математической физики, например задачи о стационарном распределении температуры в твердом теле, задачи диффузии, задачи о распределении электростатического поля в непроводящей среде при наличии электрических зарядов и многие другие.
Для решения эллиптических уравнений в случае нескольких измерений используют численные методы, позволяющие преобразовать дифференциальные уравнения или их системы в системы алгебраических уравнений. Точность решения определяется шагом координатной сетки, количеством итераций и разрядной сеткой компьютера [1]
Видео:7.2 Задача 1. Краевая задача для уравнения ПуассонаСкачать

Цель публикации получить решение уравнения Пуассона для граничных условий Дирихле и Неймана, исследовать сходимость релаксационного метода решения на примерах.
Уравнение Пуассона относится к уравнениям эллиптического типа и в одномерном случае имеет вид [1]:

где x – координата; u(x) – искомая функция; A(x), f(x) – некоторые непрерывные функции координаты.
Решим одномерное уравнение Пуассона для случая А = 1, которое при этом принимает вид:
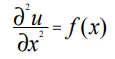
Видео:9. Уравнение ПуассонаСкачать

Зададим на отрезке [xmin, xmax] равномерную координатную сетку с шагом ∆х:
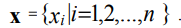
Граничные условия первого рода (условия Дирихле) для рассматриваемой задачи могут быть представлены в виде:

где х1, xn – координаты граничных точек области [xmin, xmax]; g1, g2 – некоторые
константы.
Граничные условия второго рода (условия Неймана) для рассматриваемой задачи могут быть представлены в виде:
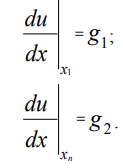
Видео:Практическое занятие. Численное решение уравнений Лапласа и ПуассонаСкачать

Проводя дискретизацию граничных условий Дирихле на равномерной координатной сетке (3) с использованием метода конечных разностей, получим:
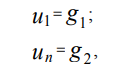
где u1, un – значения функции u(x) в точках x1, xn соответственно.
Проводя дискретизацию граничных условий Неймана на сетке (3), получим:

Проводя дискретизацию уравнения (2) для внутренних точек сетки, получим:

Видео:7.9 Задача 8. Краевая задача для уравнения ПуассонаСкачать

где ui, fi – значения функций u(x), f(x) в точке сетки с координатой xi.
Таким образом, в результате дискретизации получим систему линейных алгебраических уравнений размерностью n, содержащую n – 2 уравнения вида (8) для внутренних точек области и уравнения (6) и (7) для двух граничных точек [1].
Ниже приведен листинг на Python численного решения уравнения (2) с граничными условиями (4) – (5) на координатной сетке (3).
Разработанная мною на Python программа удобна для анализа граничных условий.Приведенный алгоритм решения на Python использует функцию Numpy — u=linalg.solve(a,b.T).T для решения системы алгебраических уравнений, что повышает быстродействие при квадратной матрице . Однако при росте числа измерений необходимо переходить к использованию трех диагональной матрицы решение для которой усложняется даже для очень простой задачи, вот нашёл на форуме такой пример:
Программа численного решения на равномерной по каждому направлению сетки задачи Дирихле для уравнения конвекции-диффузии
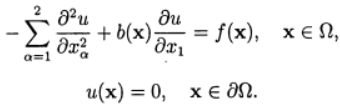
Видео:Задача Дирихле для круга. Уравнение ЛапласаСкачать

Используем аппроксимации центральными разностями для конвективного слагаемого и итерационный метод релаксации.для зависимость скорости сходимости от параметра релаксации при численном решении задачи с /(х) = 1 и 6(х) = 0,10. В сеточной задаче:

Представим матрицу А в виде суммы диагональной, нижней треугольной и верхней треугольных матриц:
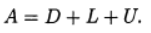
Метод релаксации соответствует использованию итерационного метода:

При 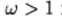

На графике показана зависимость числа итераций от параметра релаксации для уравнения Пуассона (b(х) = 0) и уравнения конвекции-диффузии (b(х) = 10). Для сеточного уравнения Пуассона оптимальное значении параметра релаксации находится аналитически, а итерационный метод сходиться при 
- Приведено решение эллиптической задачи на Python с гибкой системой установки граничных условий
- Показано что метод релаксации имеет оптимальный диапазон (
) параметра релаксации.
Ссылки:
- Рындин Е.А. Методы решения задач математической физики. – Таганрог:
Изд-во ТРТУ, 2003. – 120 с. - Вабищевич П.Н.Численные методы: Вычислительный практикум. — М.: Книжный дом
«ЛИБРОКОМ», 2010. — 320 с.
20. Метод установления решения задачи Дирихле для уравнения Пуассона. Схема переменных направлений
- Ростислав Водосвятский 5 лет назад Просмотров:
Видео:7.6 Задача 5. Краевая задача для уравнения ПуассонаСкачать

1 Варианты заданий 0. Метод установления решения задачи Дирихле для уравнения Пуассона. Схема переменных направлений 0.1. Постановка задачи Рассматривается задача Дирихле для эллиптического уравнения Lu = f(x, ), (x, ) G, (1) u = µ(x, ), (x, ) Γ. () Пусть G = G + Γ = прямоугольник, а Lu = ( p (x, ) u ) + ( q(x, ) u ), (3) x x p (x, ), q(x, ) достаточно гладкие функции, 0 2 так что Lu = L 1 u + L u. Операторы L 1 и L заменим разностными операторами Λ 1 и Λ Здесь Λ 1 u = p i+ 1 j u i+1j u h x u +1 u Λ u = q + 1 h q 1 u u i 1j p i 1 j, (5) h x u u 1 h. (6) Обозначим p i+ 1 j = p(x i + h x /, j ), p i 1 j = p(x i h x /, j ), q + 1 = q(x i, j + h /), q 1 = q(x i, j h /). Λu = Λ 1 u + Λ u, 1 i N x 1, 1 j N 1. Если u(x, ) имеет не менее четырех непрерывных ограниченных в рассматриваемой области G производных по x и по, а p(x, ) и q(x, ) не менее трех, то разностный оператор Λ аппроксимирует дифференциальный L со вторым порядком, т. е. Lu Λu = O( h ), h = h x + h. Итак, решение задачи (1)-() свелось к решению разностной задачи Дирихле (Λ 1 u + Λ u ) = f, 1 i N x 1, 1 j N 1 (7) при граничных условиях u i0 = µ(x i, 0), 0 i N x, u in = µ(x i, l ), 0 i N x, u 0j = µ(0, j ), 0 j N 1, u Nxj = µ(l x, j ), 0 j N 1. (8) 0.3. Метод установления решения задачи Дирихле для уравнения Пуассона Для вычисления решений многих стационарных задач математической физики, описывающих равновесные состояния, рассматриваются последние как результат установления развивающегося во времени процесса, расчет которого оказывается проще, чем прямой расчет равновесного состояния. Рассмотрим вспомогательную нестационарную задачу о распространении тепла u = L 1 u + L u + f(x, ), t (9) u Γ = µ(x, ), u(x,, 0) = u 0 (x, ), где f(x, ) имеет прежний смысл, а u 0 (x, ) произвольно. Поскольку источники тепла f(x, ) и температура на границе µ(x, ) не зависят от времени, то естественно ожидать, что и решение u(x,, t) с течением времени будет меняться все медленнее, распределение температур в пределе при t превратится в равновесное распределение температуры u(x, ), описываемое исходной задачей (1)-(). Надо решать задачу до тех пор, пока ее решение не перестанет меняться в пределах интересующей нас точности. Рассмотрим вначале разностную схему, с помощью которой могла бы решаться задача (7)-(8), но на практике ее не применяют по указанным в п. 0. причинам. 0.. Двухслойная схема с весами Аппроксимируем задачу (9) разностной схемой u k τ = Λ(σ + (1 σ)u k ) + f(x i, j ), 1 (10) 1 При решении стационарных задач методом установления k номер итерации, а τ итерационный параметр, который выбирается из соображений точности аппроксимации и быстроты сходимости.
3 i = 1. N x 1, j = 1. N 1, k = 0, 1. i0 = µ(x i, 0), 0 i N x, in = µ(x i, l ), 0 i N x, 0j = µ(0, j ), 1 j N 1, N xj = µ(l x, j ), 1 j N 1. Решение при k = 0 находится из начального условия в (9) (11) Рассмотрим два варианта значений параметра σ. u 0 = u 0 (x i, j ), i = 0, 1. N x, j = 0, 1. N. а) При σ = 0 получаем явную схему и решение во внутренних узлах сетки вычисляется по формуле = u k + τ(λ 1 u k + Λ u k ) + τf(x i, j ), (1) i = 1. N x 1, j = 1. N 1, k = 0, 1. Схема (1) условно устойчива при τ Ah. Общее число действий при переходе со слоя на слой пропорционально числу узлов сетки, т. е. O(N x N ) схема экономичная. б) При σ = 1 получаем неявную схему. Она устойчива при любых h и τ. Для определения на каждом слое линейную систему получаем τ(λ 1 + Λ ) = u k + τf(x i, j ), (13) i = 1. N x 1, j = 1. N 1, k = 0, 1. Матрица этой системы пятидиагональная и решать систему можно методом матричной прогонки или методом исключения Гаусса, который при учете специального вида матрицы требует O(N xn ) действий, т. е. схема не является экономичной Схема переменных направлений Эта схема сочетает лучшие качества явной схемы экономичность и неявной устойчивость. Наряду с основными значениями u k и uk+1 вводится промежуточное значение /, которое формально можно рассматривать как значение при t = t k+ 1 = t k + τ. Решение задачи в этом случае сводится к решению двух систем вида (1)-(15) с трехдиагональными матрицами. u k+ 1 u k τ/ = Λ 1 u k+ 1 + Λ u k + f(x i, j ), (1) 1 i N x 1, 1 j N 1. 3
4 u k+ 1 τ/ = Λ 1 u k+ 1 + Λ + f(x i, j ), (15) 1 i N x 1, 1 j N 1. k = 0, 1. В граничных узлах решение должно принимать заданные в (11) значения. Схема (1) неявна по направлению x и явна по направлению, а схема (15) явна по направлению x и неявна по направлению, что позволяет использовать для нахождения решения одномерные прогонки. Система (1) с учетом граничных условий (11) может быть записана в следующем виде: u k+ 1 0j = µ(0, j ), где A u k+ 1 i 1j B u k+ 1 + C u k+ 1 i+1j = G k+ 1, 1 i N x 1, u k+ 1 N xj = µ(l x, j ) (16) G k+ 1 = u k τ (Λ u k + f(x i, j )), (17) 1 j N 1. В итоге при каждом 1 j N 1 получили линейную замкнутую систему (N x + 1)-го порядка относительно u k+ 1 0j, u k+ 1 1j. u k+ 1 N xj. Матрица системы 3-х диагональная и решать систему следует методом прогонки. Прогонки осуществляются вдоль строк (рис. ). u k u k+ 1 l Рис. l x x При j = 0, j = N решения находятся из (11): u k+ 1 i0 = µ(x i, 0, t k+ 1 ), 0 i N x, u k+ 1 in = µ(x i, l, t k+ 1 ), 0 i N x. Система (15) с учетом граничных условий (11) может быть записана в следующем виде: i0 = µ(x i, 0), A 1 B + C +1 = G k+1, 1 j N 1, in = µ(x i, l ), где (18) (19) G k+1 = u k+ 1 τ (Λ 1u k+ 1 + f(x i, j )), (0) 1 i N x 1,
📸 Видео
Уравнения математической физики 15+16 Задача Дирихле для уравнения Лапласа - Пуассона в кругеСкачать

7.3 Задача 2. Краевая задача для уравнения ПуассонаСкачать

Кобельков Г. М. - Численные методы. Часть 2 - Численные методы для эллиптических уравненийСкачать

Задача Дирихле и НейманаСкачать

Численное решение задачи Коши методом ЭйлераСкачать

7.5 Задача 4. Краевая задача для уравнения ПуассонаСкачать

7.8 Задача 7. Краевая задача для уравнения ПуассонаСкачать

Шапошникова Т. А. - Уравнения с частными производными - Вариационный метод решения задачи ДирихлеСкачать

29. Адиабатический процесс. Уравнение ПуассонаСкачать

Уравнение Пуассона и задача ДирихлеСкачать

Кобельков Г. М. - Численные методы. Часть 2 - Численные методы для эллиптических уравненийСкачать

6.2 Решение задач для уравнения Лапласа в круге, вне круга и в кольцеСкачать
6-2. Метод сетокСкачать

УМФ, 01.12, решение задач Лапласа и Пуассона в случае неоднородных граничных условийСкачать