Привет, Хабр! Некоторое время назад увлекся глубоким обучением и стал потихоньку изучать tensorflow. Пока копался в tensorflow вспомнил про свою курсовую по параллельному программированию, которую делал в том году на 4 курсе университета. Задание там формулировалось так:
Линейная начально-краевая задача для двумерного уравнения теплопроводности:
Хотя правильнее было бы назвать это уравнением диффузии.
Задачу тогда требовалось решить методом конечных разностей по неявной схеме, используя MPI для распараллеливания и метод сопряженных градиентов.
Я не специалист в численных методах, пока не специалист в tensorflow, но опыт у меня уже появился. И я загорелся желанием попробовать вычислять урматы на фреймворке для глубокого обучения. Метод сопряженных градиентов реализовывать второй раз уже не интересно, зато интересно посмотреть как с вычислением справится tensorflow и какие сложности при этом возникнут. Этот пост про то, что из этого вышло.
Видео:Численное решение уравнения теплопроводностиСкачать
Численный алгоритм
Разностная схема:
Чтобы проще было расписывать, введем операторы:
Явная разностная схема:
В случае явной разностной схемы для вычисления используются значения функции в предыдущий момент времени и не требуется решать уравнение на значения . Однако такая схема менее точная и требует значительно меньший шаг по времени.
Неявная разностная схема:
Перенесем в левую сторону все связанное с , а в правую и домножим на :
По сути мы получили операторное уравнение над сеткой:
что, если записать значения в узлах сетки как обычный вектор, является обычной системой линейных уравнений (). Значения в предыдущий момент времени константы, так как уже рассчитаны.
Для удобства представим оператор как разность двух операторов:
Заменив на нашу оценку , запишем функционал ошибки:
где — ошибка в узлах сетки.
Будем итерационно минимизировать функционал ошибки, используя градиент.
В итоге задача свелась к перемножению тензоров и градиентному спуску, а это именно то, для чего tensorflow и был задуман.
Видео:Решение уравнения теплопроводности в одномерной постановке в ExcelСкачать
Реализация на tensorflow
Кратко о tensorflow
В tensorflow сначала строится граф вычислений. Ресурсы под граф выделяются внутри tf.Session. Узлы графа — это операции над данными. Ячейками для входных данных в граф служат tf.placeholder. Чтобы выполнить граф, надо у объекта сессии запустить метод run, передав в него интересующую операцию и входные данные для плейсхолдеров. Метод run вернет результат выполнения операции, а также может изменить значения внутри tf.Variable в рамках сессии.
tensorflow сам умеет строить графы операций, реализующие backpropagation градиента, при условии, что в оригинальном графе присутствуют только операции, для которых реализован градиент (пока не у всех).
Сначала код инициализации. Здесь производим все предварительные операции и считаем все, что можно посчитать заранее.
По-хорошему надо было считать значения функции на краях заданными и оптимизировать значения функции только во внутренней области, но с этим возникли проблемы. Способа сделать оптимизируемым только часть тензора не нашлось, и у операции присвоения значения срезу тензора не написан градиент (на момент написания поста). Можно было бы попробовать хитро повозиться на краях или написать свой оптимизатор. Но и просто добавление разности на краях значений функции и краевых условий в функционал ошибки хорошо работает.
Стоит отметить, что метод с адаптивным моментом показал себя наилучшим образом, пусть функционал ошибки и квадратичный.
Вычисление функции: в каждый момент времени делаем несколько оптимизационных итераций, пока не превысим maxiter или ошибка не станет меньше eps, сохраняем и переходим к следующему моменту.
Запуск:
Видео:Лекция №1.1 Явная и неявная схемы для уравнения теплопроводностиСкачать
Результаты
Условие как и оригинальное, но без в уравнении:
Что легко правится в коде:
Разницы почти нет, потому что производные имеют большие порядки, чем сама функция.
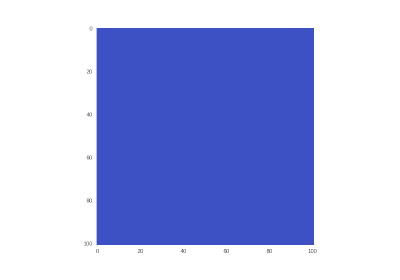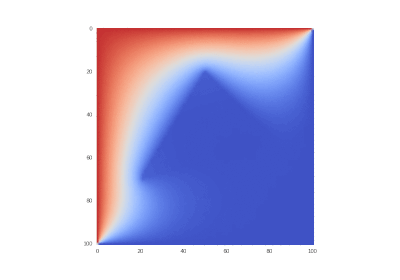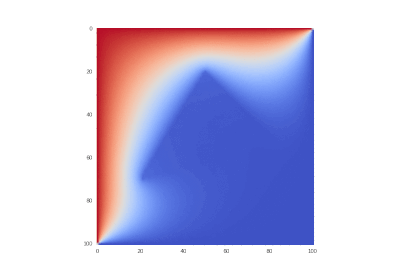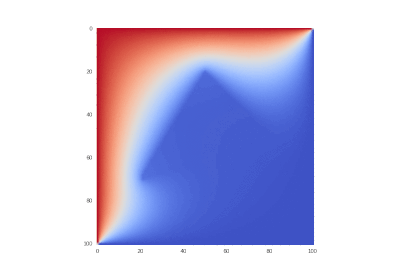
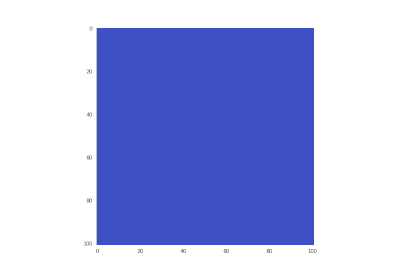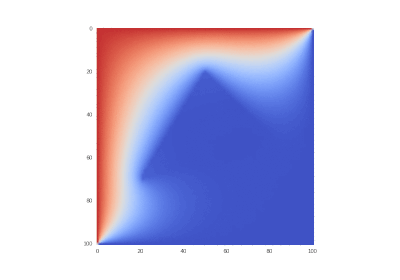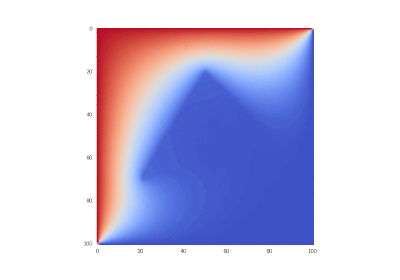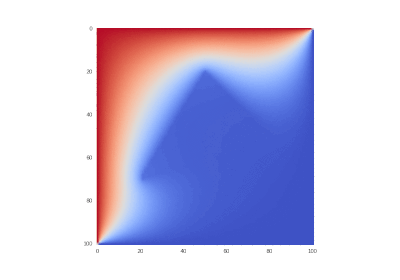
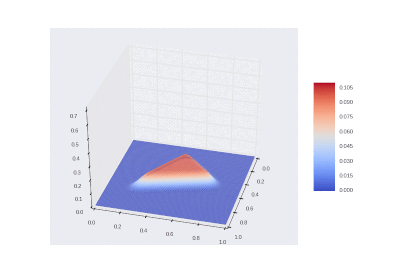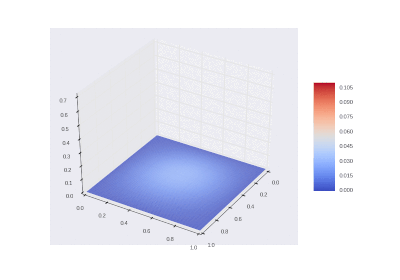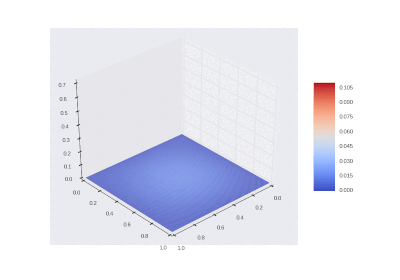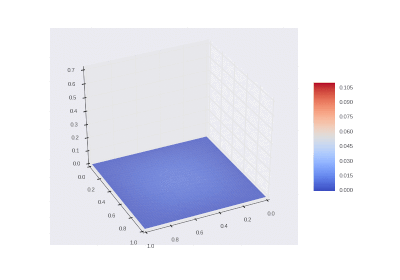
Условие с одним нагревающимся краем:
Условие с остыванием изначально нагретой области:
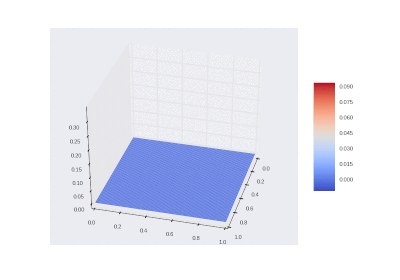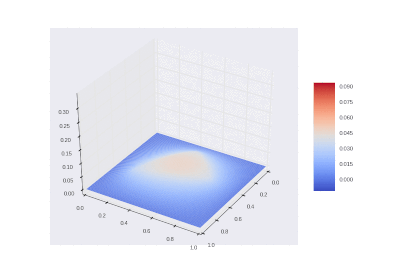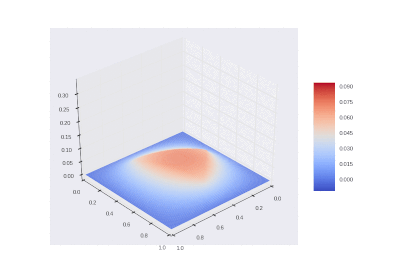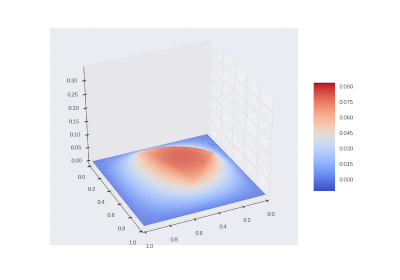
Условие с включением нагрева в области:
Видео:Решение уравнения теплопроводности методом конечных разностейСкачать
Рисование гифок
Функция рисования 3D-гифки:
В основной класс добавляем метод, возвращающий U в виде pandas.DataFrame
Функция рисования 2D-гифки:
Стоит отметить, что оригинальное условие без использования GPU считалось 4м 26с, а с использованием GPU 2м 11с. При больших значениях точек разрыв растет. Однако не все операции в полученном графе GPU-совместимы.
- Intel Core i7 6700HQ 2600 МГц,
- NVIDIA GeForce GTX 960M.
Посмотреть, какие операции на чем выполняются, можно с помощью следующего кода:
Это был интересный опыт. Tensorflow неплохо показал себя для этой задачи. Может быть даже такой подход получит какое-то применение — всяко приятнее писать код на питоне, чем на C/C++, а с развитием tensorflow станет еще проще.
Видео:Численные методы математической физики - Решение смешанной задачи для уравнения теплопроводностиСкачать
Решение уравнения теплопроводности по алгоритму Томаса
Я пытаюсь решить дифференциальное уравнение теплопроводности, используя алгоритм Томаса.
Физическая проблема: У нас есть штекер, температура на левой стороне 0 температура правой стороны 1 ,
Для алгоритма Томаса я написал функцию, которая принимает три QVector а также int значение суммы уравнений.
Моя проблема:
когда я компилирую и запускаю его, я получаю это:
Снова и снова в цикле.
Я понятия не имею, почему я получаю это.
Может быть, моя ошибка в назначении Tn результат моего Thomas-метода-функции?
или в реализации метода Томаса? или в граничных условиях?
Видео:12. Как остывает шар (решение уравнения теплопроводности)Скачать
Решение
Граничные условия должны действовать на векторы
так что T [0] должно быть 0, а T [N-1] должно быть 1. Мы можем сделать это следующим образом:
и благодаря этому T [0] всегда будет равно нулю, а T [N-1] будет равно 1;
И в статье, где я читал о методе Томаса, первым шагом было отрицание главной диагонали, я сделал это, но затем в конце функции я должен сделать обратное, так:
и мы можем использовать эту функцию снова, это не совсем оптимально, но работает стабильно.
Тогда весь код будет выглядеть так:
и на последнем шаге мы собираемся получить абсолютно «физические» результаты:
Видео:Решение уравнения теплопроводности в одномерной постановке в Excel с применением неявной схемыСкачать
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
| Вход Регистрация | Donate FAQ Правила Поиск |
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву , правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
Видео:Уравнение в частных производных Уравнение теплопроводностиСкачать
Одномерное уравнение теплопроводности. Численное решение.
 |
Доброго дня суток!
Хотелось бы подробно описать интересующую меня проблему и найти такой же подробный ответ на него. Некоторые вещи мне удалось понять самостоятельно благодаря большому количеству имеющейся в моем запасе литературы:
Теперь, непосредственно само задание(ссылка на скан листа, если что-то не понятно), которое я перепишу в формате 
Здесь можно увидеть в самом верху, в рамке находится уравнение теплопроводности: 
далее приводится рисунок, отображающий начальное условие системы при t=0:
Заранее оговаривается метод, с помощью которого мы будем численно решать это уравнение:
Сеточные методы на Эйлеровых схемах (явная схема).
Конечно, нужно будет определить устойчивость схемы и выяснить, при каких критических значениях 
эта схема будет сходиться(ответ уже найден и равен 
, где 
— шаг по времени(), 
— шаг по пространственной координате)
Далее приводится 3 уравнения, назначение которых мне не совсем ясно, но имеются догадки:
Видимо, нужно еще варьировать коэффициент 
— коэффициент теплопроводности в зависимости от этой системы уравнений, описанной выше.
Суть всего этого задания — реализовать в виде приложения на языке Си/С++, которое показывает зависимость точности решения от шага интегрирования на примере этого самого уравнения теплопроводности , что не составляет труда, если задание понятно и чётко сформулировано. Однако мои текущие познания в области вычислительной математики довольно скудны, поэтому мне довольно проблематично связать текущие соотношения в единую систему.
Во-первых, нужно задать граничные условия для нашего уравнения теплопроводности(исходя из рисунка):
Допустим 
где 
(здесь подразумевается, что a и b — концы стержня)
Во-вторых, нужно ввести пространственно-временную сетку, которая будет представлять из себя матрицу, причем каждая строка её[матрицы] характеризует значения уравнения при каком-либо времени 
. (здесь поправьте меня, если я не правильно понял смысл всех этих сеток)
В-третьих, мы переписываем уравнение теплопроводности в виде разностной схемы: 
откуда мы можем найти 
при условии, что нам известно начальное распределение температуры на предыдущем временном слое(например на 
).
В-четвертых, следует учитывать еще эти три уравнения, связанные с самим коэффициентом теплопроводности. Таким образом задача усложняется — требуется понять, каким именно образом следует организовать эту связь и как мы можем вообще их применить либо хотя бы выразить. Я предполагаю, что начальный коэффициент теплопроводности (та самая 
) должен задаваться в начале, а затем уже выводятся и находятся остальные значения уравнений.
Возникает некоторое количество логичных вопросов:
1. На графике нарисован «стержень» — с равномерной начальной температурой по всей его длине. Что будет означать профиль графика в последующие моменты времени — нагрев окружающей среды и остужение самого стержня?
2. Достаточно ли я описал задачу(для описания её непосредственно в дискретной форме, в ЭВМ) и нет ли где «подводных» камней, либо неопределенности касаемо условий задачи?
3. Каким образом проще и понятнее ввести дополнительные условия для коэффициента теплопроводности(имеются в виду 3 вышеприведенных уравнения)?
4. Мелкие, но необходимые для целостной картины вопросы, описанные выше, в тексте.
5. Правильность моих рассуждений.
Заранее спасибо, если вы смогли осилить этот текст. Просьба: описывайте как можно более подробнее( желательно на пальцах ) свои мысли и объяснения.
В случае успеха я постараюсь выложить понятный алгоритм действий при решении задач такого рода.
🎦 Видео
Решение задачи Коши для уравнения теплопроводности (Часть 1)Скачать
Решение задачи Коши для уравнения теплопроводности (Часть 2)Скачать
Решение первой краевой задачи для неоднородного уравнения теплопроводности.Скачать
8.1 Решение уравнения теплопроводности на отрезкеСкачать
15. Решение уравнения теплопроводности в кругеСкачать
Решение уравнения теплопроводности методом клеточных автоматов.Скачать
Метод конечных элементов (Часть 1) | Пример реализации для уравнения теплопроводностиСкачать
Метод Ньютона (касательных) и хорд Численное решение уравнения c++Скачать
Стационарное решение одномерного уравнения теплопроводности.Скачать
Решение задачи теплопроводности методом конечных разностейСкачать
Метод Фурье для неоднородного уравнения теплопроводностиСкачать
Численное решение задачи Коши методом ЭйлераСкачать
