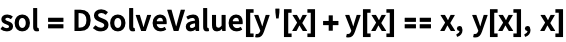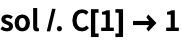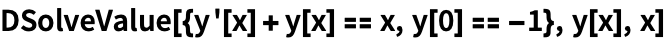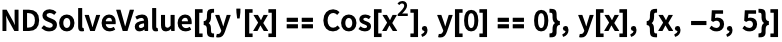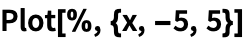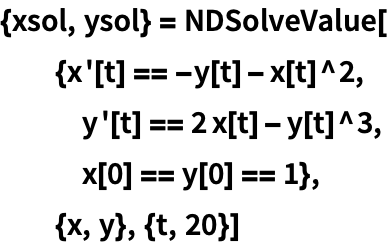Численное решение дифференциальных уравнений wolfram

Математика с WolframAlpha ® . Объяснения с примерами.

Численное решение обыкновенных дифференциальных уравнений в Wolfram|Alpha

solve (метод интегрирования) [шаг интегрирования] [отрезок интегрирования]

Обязательные параметры — само дифференциальное уравнение, начальные условия и численный метод интегрирования.

Не забудьте, что количество начальных условий должно совпадать с порядком уравнения. Иначе, Wolfram Alpha автоматически подставит в запрос свои начальные или краевые условия.

Рекомендуется указывать явно отрезок интегрирования. Без этого Wolfram Alpha автоматически выполнит 10 шагов интегрирования по умолчанию. Можно явно указать шаг интегрирования. В противном случае, Wolfram Alpha установит шаг интегрирования по умолчанию, как в следующем примере:

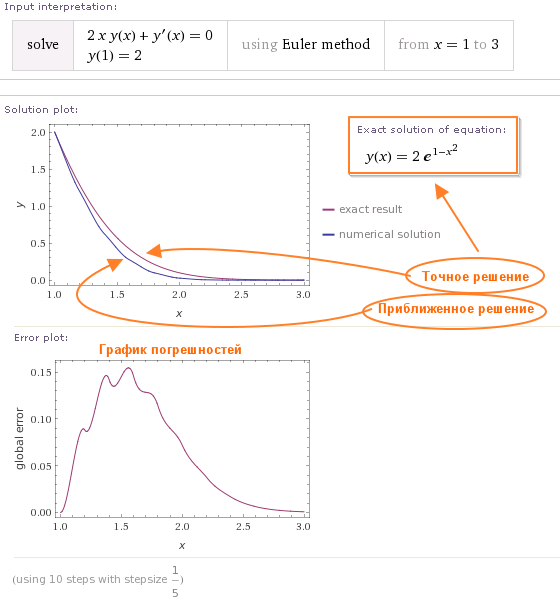
Когда дифференциальное уравнение, которое вы решаете численным методом, допускает также аналитическое решение, тогда по запросу solve система Wolfram Alpha выводит точную и приближенную интегральные кривые уравнения, соответствующие заданным начальным условиям, а также график погрешностей, таблицу значений искомой функции, таблицу погрешностей, и, конечно, само аналитическое решение:

Кроме того, здесь Wolfram Alpha выводит таблицу для сравнения погрешностей всех численных методов, которые использует система (в крайней точке интервала интегрирования дифференциального уравнения):

В рассмотренном примере шаг интегрирования, равный 0.2, был выбран автоматически. Выше было сказано, что можно явно указать нужный шаг интегрирования. Причем, нужно выбирать его так, чтобы на заданном отрезке умещалось не менее, чем 10 шагов интегрирования. Уменьшая шаг интегрирования, можно получать численные решения с желаемой точностью точностью:

Численные решения дифференциальных уравнений, рассмотренные выше, были получены простейшим методом — методом Эйлера (Euler method). Как мы видели выше, Wolfram Alpha реализует и другие численные методы интегрирования дифференциальных уравнений. Посмотрите примеры (по ссылке):

• Euler method — метод Эйлера;
• midpoint method — метод средних точек, модифицированный метод Эйлера;
• Heun’s method (метод Хойна, вариант модифицированного метода Эйлера)
• third‐order Runge‐Kutta method (метод Рунге-Кутты третьего порядка)
• fourth‐order Runge‐Kutta method (метод Рунге-Кутты четвертого порядка)
• Runge‐Kutta‐Fehlberg method (метод Рунге-Кутты-Фелберга, RKF method )
• Bogacki‐Shampine method
• Dormand‐Prince method (DOPRI method)
• backward Euler method
• implicit midpoint method

С помощью Wolfram Alpha, можно решать не только обыкновенные дифференциальные уравнения 1-го порядка (ОДУ-1), но и обыкновенные дифференциальные уравнения высших порядков. Например, вот так Wolfram Alpha решает обыкновенное дифференциальное уравнение 3-го порядка:

Таким образом, численное решение обыкновенных дифференциальных уравнений в системе Wolfram Alpha является достаточно простой стандартной процедурой, соблюдение которой гарантирует правильный результат.

Видео:Численное решение задачи Коши методом ЭйлераСкачать

Использование Wolfram Mathematica в решении дифференциальных уравнений

Саратовский национальный исследовательский государственный университет имени Н.Г. Чернышевского

NovaInfo55, с. 5-9
Опубликовано 20 ноября 2016
Раздел: Физико-математические науки
Просмотров за месяц: 49
CC BY-NC

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

Аннотация

В статье рассматриваются примеры решения обыкновенных дифференциальных уравнений в системе Wolfram Mathematica.

Видео:КиЯ 0.18 | Решение уравнения и отображение его корней в Wolfram LanguageСкачать

Ключевые слова

Видео:01.02. Модель SIR. Численное решение системы дифференциальных уравнений с помощью SciPyСкачать

Текст научной работы

Системы компьютерной математики (Maple, Mathematica, MatLab, Derive и др.) применяются в различных областях науки. Они содержат процедуры для численных и аналитических расчетов, средства программирования, визуализации. В настоящее время пакеты прикладных программ используются не только при решении численных задач, но и при доказательстве теорем. Системы компьютерной математики используются в решении математических проблем в работах Д.С. Воронова, О.П. Гладуновой, Е.С. Корнева, М.В. Куркиной, Е.Д. Родионова, Я.В. Славолюбовой, В.В. Славского, Н.К. Смоленцева, Л.Н. Чибриковой и др.

Система компьютерной математики Wolfram Mathematica является одним из наиболее распространенных программных средств, которое позволяет выполнять численные, символьные вычисления, имеет развитую двумерную и трехмерную графику, а также встроенный язык программирования высокого уровня. Для знакомства с языком программирования Wolfram Language рекомендуется интернет-ресурс Wolfram Language & System «Documentation Center» (http://reference.wolfram.com/language/). Выбирая раздел, можно познакомиться с имеющимися командами для решения задач и с примерами их использования. Примеры использования Mathematica в решении геометрических задач приведены в 5.

Система Mathematica обладает обширными возможностями решения обыкновенных дифференциальных уравнений и их систем в символьном виде. Для этого используется функция DSolve, в алгоритме которой реализовано большинство известных на сегодняшний день аналитических методов.

Пример 1. Решим дифференциальное уравнение и построим график решений при различных значениях постоянной.

Пример 2. Решим уравнение y’=frac

Попытаемся решить уравнение с помощью функции DSolve:

В данном случае функция DSolve не может решить нелинейное уравнение. Поэтому запишем уравнение в виде:

и будем интегрировать обе части уравнения:

Следовательно, общее решение уравнения примет вид

-(-2+y^2)cos y+2ysin y=x-10ln (1-x)+13ln(2-x)+C

Пример 3. Решим дифференциальное уравнение и построим поле направлений и график решения уравнения при различных значениях константы.

Построим таблицу решений, заменив С[1] на a, где a изменяется от -2 до 2 с шагом 0,5:

Отобразим два графика одновременно и покажем, что векторы поля направлений являются касательными к решениям дифференциального уравнения:

Система Wolfram Mathematica используется для решения дифференциальных уравнений не только в математике, но и актуальна в других научных областях. Ее можно применять и в механике, в частности, для решения различных постановок задач, где в качестве математических объектов используются дифференциальные уравнения. В работах [6,7] рассмотрены уравнения движения мембран и акустических сред в виде обыкновенных дифференциальных уравнений. Для их решения может быть использована система компьютерной математики Wolfram Mathematica.

Видео:Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

Читайте также

Математическая подготовка студентов в вузе в контексте будущей профессиональной деятельности

Использование прикладных программ при изучении математической статистики

Применение систем компьютерной математики при изучении комплексного анализа

Организация самостоятельной работы студентов в условиях информационно-образовательной среды вуза

Системы компьютерной математики в решении дифференциальных уравнений

Видео:Численное решение дифференциальных уравнений (задачи Коши)Скачать

Список литературы

1. Букушева А.В. Использование Mathematica для описания геометрии динамических систем // Математика и ее приложения: фундаментальные проблемы науки и техники : сборник трудов всероссийской конференции, Барнаул, 24 — 26 ноября 2015. — Барнаул : Изд-во Алт. ун-та, 2015. С. 248-249.
2. Букушева А.В. Применение Wolfram Language для выделения специальных классов почти контактных метрических структур // Компьютерные науки и информационные технологии : Материалы Междунар. науч. конф. — Саратов : Издат. центр.»Наука», 2016. С. 105-107.
3. Букушева А.В. Использование систем компьютерной математики для решения геометрических задач сложного уровня // Информационные технологии в образовании: Материалы VI Всероссийской научно-практической конференции. – Саратов: ООО «Издательский центр «Наука»». 2014. – С. 76-77.
4. Букушева А.В. Решение учебно-исследовательских задач с использованием систем компьютерной математики // Информационные технологии в образовании: Материалы VII Всеросс. научно-практ. конф. – Саратов: ООО «Издательский центр «Наука»», 2015. С.185-187.
5. Букушева А.В. Учебно-исследовательские задачи в продуктивном обучении будущих бакалавров-математиков // Образовательные технологии. 2016. №2. С. 16-26.
6. Вельмисова А.И. Распространение и отражение гармонических волн в плоском акустическом слое с гибкими стенками в случае разрыва упругих свойств на одной из стенок // Математика. Механика: Сб. науч. тр. Саратов: Изд-во Сарат. ун-та, 2010. Вып.12. С. 136-140.
7. Вельмисова А.И., Вильде М.В., Кириллова И.В. Распространение и отражение гармонических волн в плоском акустическом слое с кусочно-неоднородными гибкими стенками // Известия Саратовского университета. Новая серия. Серия: Математика. Механика. Информатика. 2011. Т.11. №4. С. 68-73.

Видео:12.01 Решение систем ДУ в Wolfram MathematicaСкачать

Цитировать

Зинина, А.И. Использование Wolfram Mathematica в решении дифференциальных уравнений / А.И. Зинина. — Текст : электронный // NovaInfo, 2016. — № 55. — С. 5-9. — URL: https://novainfo.ru/article/8754 (дата обращения: 19.02.2022).

Видео:5 Численное решение дифференциальных уравнений Part 1Скачать

Поделиться

Электронное периодическое издание зарегистрировано в Федеральной службе по надзору в сфере связи, информационных технологий и массовых коммуникаций (Роскомнадзор), свидетельство о регистрации СМИ — ЭЛ № ФС77-41429 от 23.07.2010 г.

Соучредители СМИ: Долганов А.А., Майоров Е.В.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Дифференциальные уравнения

Язык Wolfram позволяет решать обыкновенные дифференциальные уравнения, дифференциальные уравнения в частных производных и уравнения с запаздыванием.

Функция DSolveValue возвращает решение дифференциального уравнения в общем виде:

Out[1]=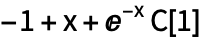

Используем символ /. для замены константы:

Out[2]=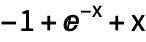

Или добавим начальные условия для получения частного решения:

Out[3]=

Функция NDSolveValue позволяет находить численные решения:

Out[1]=

Объект InterpolatingFunction можно визуализировать без дополнительной обработки:

Out[2]=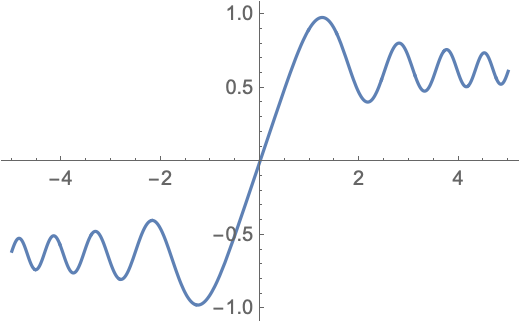

Для решения систем дифференциальных уравнений, необходимо использовать списки для задания уравнений и условий:

(Обратите внимание, что перенос уравнений на новую строку не влияет на результат.)

Out[1]=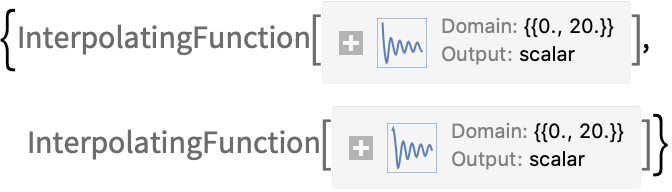

Построим решения системы в виде параметрического графика:

🎥 Видео

Сеточные методы решения дифференциальных уравнений в частных производных.Скачать

Метод ЭйлераСкачать

Python - численное решение дифференциального уравнения 1го порядка и вывод графикаСкачать

Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Численное решение дифференциальных уравнений ч.1Скачать

Решение систем Д/У: 1. Знакомство с функциями odeXYСкачать