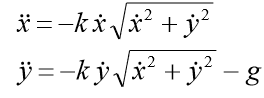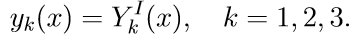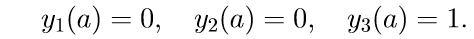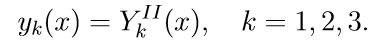Рассмотрены приемы решения обыкновенных дифференциальных уравнений (ОДУ) с помощью модуля scipy.integrate языка Python
- Краткое описание модуля scipy.integrate
- Решение одного ОДУ
- Решение системы ОДУ
- Численное решение математических моделей объектов заданных системами дифференциальных уравнений
- Введение:
- Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
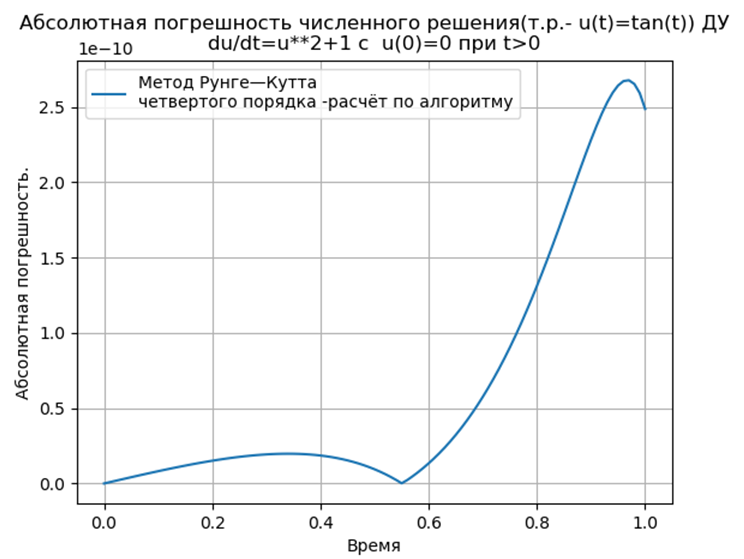
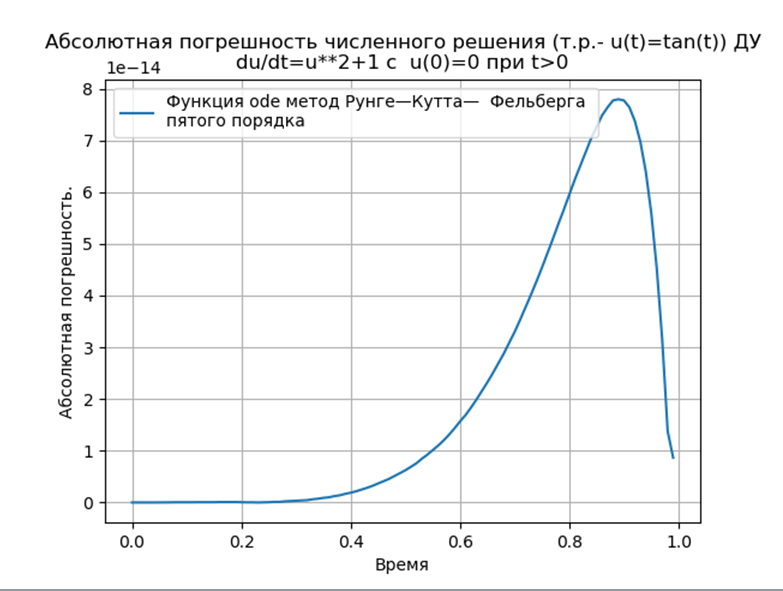
- Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
- Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
- Решение краевой задачи с поточно разделёнными краевыми условиями
- Вывод
- Руководство по SciPy: что это, и как ее использовать
- Что такое SciPy?
- NumPy vs SciPy
- Пакеты в SciPy
- Базовые функции
- Взаимодействие с NumPy
- Специальные функции
- Экспоненциальные и тригонометрические функции
- Интегральные функции
- Двойные интегральные функции
- Функции оптимизации
- Функция Розенброка
- Nelder-Mead
- Функции интерполяции
- Одномерная интерполяция
- Многомерная интерполяция
- Функции преобразования Фурье
- Функции обработки сигналов
- Линейная алгебра
- Нахождение обратной матрицы
- Нахождение определителей
- Разреженные собственные значения
- Разреженные структуры данных и алгоритмы
- Триангуляции Делоне
- Функции многомерной обработки изображений
Видео:Python - численное решение дифференциального уравнения 1го порядка и вывод графикаСкачать

Краткое описание модуля scipy.integrate
Модуль scipy.integrate имеет две функции ode() и odeint(), которые предназначены для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (т.е. задача Коши).
Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат
Видео:Численное решение задачи Коши методом ЭйлераСкачать

Решение одного ОДУ
Допустим надо решить диф. уравнение 1-го порядка
Получилось что-то такое:
Видео:01.02. Модель SIR. Численное решение системы дифференциальных уравнений с помощью SciPyСкачать

Решение системы ОДУ
Пусть теперь мы хотим решить (автономную) систему диф. уравнений 1-го порядка
Выходной массив w состоит из двух столбцов — y1(t) и y2(t).
Также без труда можно построить фазовые траектории:
Видео:Решение дифференциальных уравнений в Python. Задача о четырех жуках.Скачать

Численное решение математических моделей объектов заданных системами дифференциальных уравнений
Введение:
При математическом моделировании ряда технических устройств используются системы дифференциальных нелинейных уравнений. Такие модели используются не только в технике, они находят применение в экономике, химии, биологии, медицине, управлении.
Исследование функционирования таких устройств требуют решения указанных систем уравнений. Поскольку основная часть таких уравнений являются нелинейными и нестационарными, часто невозможно получить их аналитическое решение.
Возникает необходимость использовать численные методы, наиболее известным из которых является метод Рунге — Кутты [1]. Что касается Python, то в публикациях по численным методам, например [2,3], данных по применение Рунге — Кутты крайне мало, а по его модификации — методу Рунге-Кутта-Фельберга вообще нет.
В настоящее время, благодаря простому интерфейсу, наибольшее распространение в Python имеет функцию odeint из модуля scipy.integrate. Вторая функция ode из этого модуля реализует несколько методов, в том числе и упомянутый пятиранговый метод Рунге-Кутта-Фельберга, но, вследствие универсальности, имеет ограниченное быстродействие.
Целью настоящей публикации является сравнительный анализ перечисленных средств численного решения систем дифференциальных уравнений с модифицированным автором под Python методом Рунге-Кутта-Фельберга. В публикации так же приведены решения по краевым задачам для систем дифференциальных уравнений (СДУ).
Краткие теоретические и фактические данные по рассматриваемым методам и программным средствам для численного решения СДУ
Для одного дифференциального уравнения n – го порядка, задача Коши состоит в нахождении функции, удовлетворяющей равенству:
и начальным условиям
Перед решением эта задача должна быть переписана в виде следующей СДУ
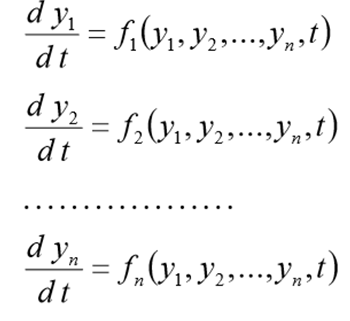
с начальными условиями
Модуль имеет две функции ode() и odeint(), предназначенные для решения систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка с начальными условиями в одной точке (задача Коши). Функция ode() более универсальная, а функция odeint() (ODE integrator) имеет более простой интерфейс и хорошо решает большинство задач.
Функция odeint() имеет три обязательных аргумента и много опций. Она имеет следующий формат odeint(func, y0, t[,args=(), . ]) Аргумент func – это имя Python функции двух переменных, первой из которых является список y=[y1,y2. yn], а второй – имя независимой переменной.
Функция func должна возвращать список из n значений функций 
Второй аргумент y0 функции odeint() является массивом (или списком) начальных значений 
Третий аргумент является массивом моментов времени, в которые вы хотите получить решение задачи. При этом первый элемент этого массива рассматривается как t0.
Функция odeint() возвращает массив размера len(t) x len(y0). Функция odeint() имеет много опций, управляющих ее работой. Опции rtol (относительная погрешность) и atol (абсолютная погрешность) определяют погрешность вычислений ei для каждого значения yi по формуле
Они могут быть векторами или скалярами. По умолчанию
Вторая функция модуля scipy.integrate, которая предназначена для решения дифференциальных уравнений и систем, называется ode(). Она создает объект ОДУ (тип scipy.integrate._ode.ode). Имея ссылку на такой объект, для решения дифференциальных уравнений следует использовать его методы. Аналогично функции odeint(), функция ode(func) предполагает приведение задачи к системе дифференциальных уравнений вида (1) и использовании ее функции правых частей.
Отличие только в том, что функция правых частей func(t,y) первым аргументом принимает независимую переменную, а вторым – список значений искомых функций. Например, следующая последовательность инструкций создает объект ODE, представляющий задачу Коши.
При построении численных алгоритмов будем считать, что решение этой дифференциальной задачи существует, оно единственно и обладает необходимыми свойствами гладкости.
При численном решении задачи Коши
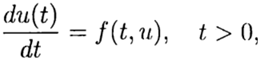

по известному решению в точке t =0 необходимо найти из уравнения (3) решение при других t. При численном решении задачи (2),(3) будем использовать равномерную, для простоты, сетку по переменной t с шагом т > 0.
Приближенное решение задачи (2), (3) в точке 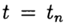

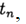


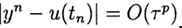

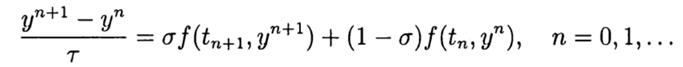
При 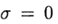
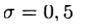
Явные схемы второго и более высокого порядка аппроксимации удобно строить, ориентируясь на метод предиктор-корректор. На этапе предиктора (предсказания) используется явная схема
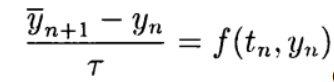
а на этапе корректора (уточнения) — схема
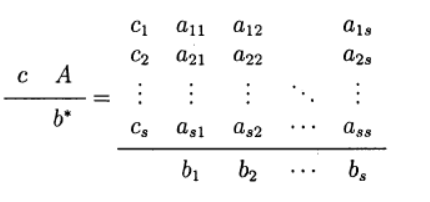
В одношаговых методах Рунге—Кутта идеи предиктора-корректора реализуются наиболее полно. Этот метод записывается в общем виде:

Формула (6) основана на s вычислениях функции f и называется s-стадийной. Если 
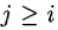

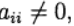

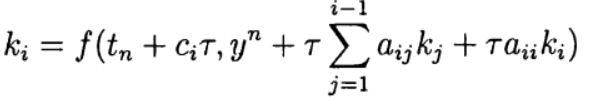
О таком методе Рунге—Кутта говорят как о диагонально-неявном. Параметры 
Одним из наиболее распространенных является явный метод Рунге—Кутта четвертого порядка

Метод Рунге—Кутта— Фельберга
Привожу значение расчётных коэффициентов 
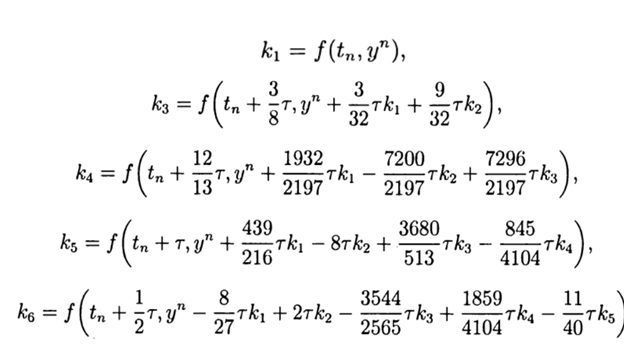
С учётом(9) общее решение имеет вид:
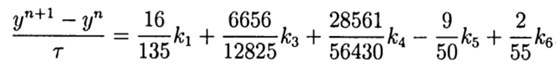
Это решение обеспечивает пятый порядок точности, остаётся его адаптировать к Python.
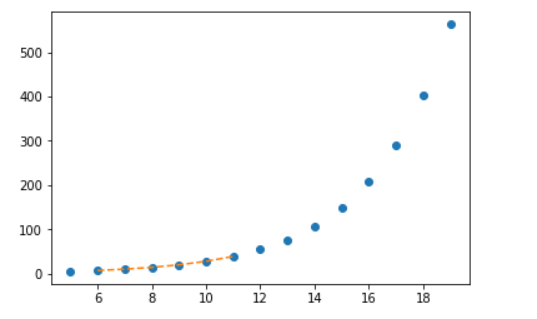
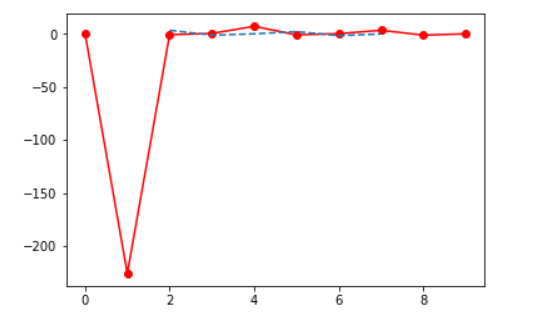
Вычислительный эксперимент по определению абсолютной погрешности численного решения нелинейного дифференциального уравнения  с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
Адаптированные к Python методы Рунге—Кутта и Рунге—Кутта— Фельберга имеют меньшую абсолютную, чем решение с применением функции odeint, но большую, чем с использованием функции edu. Необходимо провести исследование быстродействия.
Численный эксперимент по сравнению быстродействия численного решения СДУ при использовании функции ode с атрибутом dopri5 (метод Рунге – Кутты 5 порядка) и с использованием адаптированного к Python метода Рунге—Кутта— Фельберга
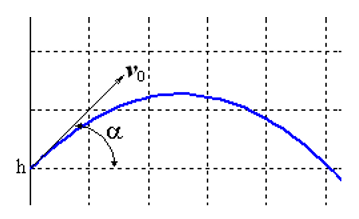
Сравнительный анализ проведём на примере модельной задачи, приведенной в [2]. Чтобы не повторять источник, приведу постановку и решение модельной задачи из [2].
Решим задачу Коши, описывающую движение тела, брошенного с начальной скоростью v0 под углом α к горизонту в предположении, что сопротивление воздуха пропорционально квадрату скорости. В векторной форме уравнение движения имеет вид
где 



Особенность этой задачи состоит в том, что движение заканчивается в заранее неизвестный момент времени, когда тело падает на землю. Если обозначить 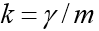
К системе следует добавить начальные условия: 

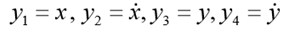
Для модельной задачи положим 
Flight time = 1.2316 Distance = 5.9829 Height =1.8542
Flight time = 1.1016 Distance = 4.3830 Height =1.5088
Flight time = 1.0197 Distance = 3.5265 Height =1.2912
Flight time = 0.9068 Distance = 2.5842 Height =1.0240
Время на модельную задачу: 0.454787
Для реализации средствами Python численного решения СДУ без использования специальных модулей, мною была предложена и исследована следующая функция:
def increment(f, t, y, tau
k1=tau*f(t,y)
k2=tau*f(t+(1/4)*tau,y+(1/4)*k1)
k3 =tau *f(t+(3/8)*tau,y+(3/32)*k1+(9/32)*k2)
k4=tau*f(t+(12/13)*tau,y+(1932/2197)*k1-(7200/2197)*k2+(7296/2197)*k3)
k5=tau*f(t+tau,y+(439/216)*k1-8*k2+(3680/513)*k3 -(845/4104)*k4)
k6=tau*f(t+(1/2)*tau,y-(8/27)*k1+2*k2-(3544/2565)*k3 +(1859/4104)*k4-(11/40)*k5)
return (16/135)*k1+(6656/12825)*k3+(28561/56430)*k4-(9/50)*k5+(2/55)*k6
Функция increment(f, t, y, tau) обеспечивает пятый порядок численного метода решения. Остальные особенности программы можно посмотреть в следующем листинге:
Время на модельную задачу: 0.259927
Предложенная программная реализация модельной задачи без использования специальных модулей имеет почти в двое большее быстродействие, чем с функцией ode, однако нельзя забывать, что ode имеет более высокую точность численного решения и возможности выбора метода решения.
Решение краевой задачи с поточно разделёнными краевыми условиями
Приведем пример некоторой конкретной краевой задачи с поточно разделенными краевыми условиями:
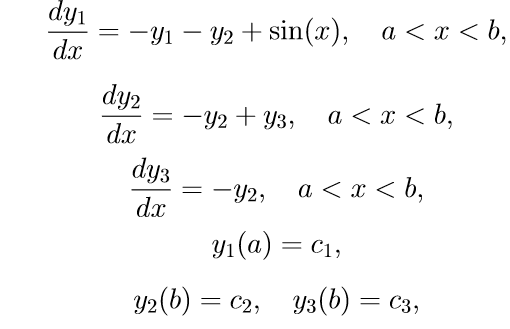
Для решения задачи (11) используем следующий алгоритм:
1. Решаем первые три неоднородные уравнения системы (11) с начальными условиями 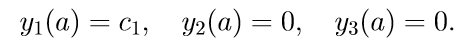
Введем обозначение для решения задачи Коши:
2. Решаем первые три однородные уравнения системы (11) с начальными условиями 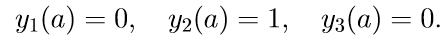
Введем обозначение для решения задачи Коши:
3. Решаем первые три однородные уравнения системы (11) с начальными условиями
Введем обозначение для решения задачи Коши:
4. Общее решение краевой задачи (11) при помощи решений задач Коши записывается в виде линейной комбинации решений: 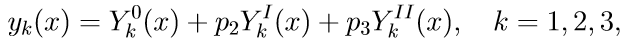
где p2, p3 — некоторые неизвестные параметры.
5. Для определения параметров p2, p3, используем краевые условия последних двух уравнений (11), то есть условия при x = b. Подставляя, получим систему линейных уравнений относительно неизвестных p2, p3:

Решая (12), получим соотношения для p2, p3.
По приведенному алгоритму с применением метода Рунге—Кутта—Фельберга получим следующую программу:
y0[0]= 0.0
y1[0]= 1.0
y2[0]= 0.7156448588231397
y3[0]= 1.324566562303714
y0[N-1]= 0.9900000000000007
y1[N-1]= 0.1747719838716767
y2[N-1]= 0.8
y3[N-1]= 0.5000000000000001
Время на модельную задачу: 0.070878
Вывод
Разработанная мною программа отличается от приведенной в [3] меньшей погрешностью, что подтверждает приведенный в начале статьи сравнительный анализ функции odeint с реализованным на Python метода Рунге—Кутта—Фельберга.
3. Н.М. Полякова, Е.В. Ширяева Python 3. Создание графического интерфейса пользователя (на примере решения методом пристрелки краевой задачи для линейных обыкновенных дифференциальных уравнений). Ростов-на-Дону 2017.
Видео:Метод ЭйлераСкачать

Руководство по SciPy: что это, и как ее использовать
Математика — это масса понятий, которые являются одновременно важными и сложными. Для работы с ними в Python есть библиотека SciPy. В этом материале вы познакомитесь с ее функциями на примерах.
Видео:Решение ОДУ 2 порядка в PythonСкачать

Что такое SciPy?
SciPy — это библиотека Python с открытым исходным кодом, предназначенная для решения научных и математических проблем. Она построена на базе NumPy и позволяет управлять данными, а также визуализировать их с помощью разных высокоуровневых команд. Если вы импортируете SciPy, то NumPy отдельно импортировать не нужно.
Видео:Python - поле направлений дифференциального уравненияСкачать

NumPy vs SciPy
И NumPy, и SciPy являются библиотеками Python, которые используются для математического и числового анализов. NumPy содержит данные массивов и операции, такие как сортировка, индексация, а SciPy состоит из числового кода. И хотя в NumPy есть функции для работы с линейной алгеброй, преобразованиями Фурье и т. д., в SciPy они представлены в полном виде вместе с массой других. А для полноценного научного анализа в Python нужно устанавливать и NumPy, и SciPy, поскольку последняя построена на базе NumPy.
Видео:Решение системы ОДУ в PythonСкачать

Пакеты в SciPy
В SciPy есть набор пакетов для разных научных вычислений:
| Название | Описание |
|---|---|
| cluster | Алгоритмы кластерного анализа |
| constants | Физические и математические константы |
| fftpack | Быстрое преобразование Фурье |
| integrate | Решения интегральных и обычных дифференциальных уравнений |
| interpolate | Интерполяция и сглаживание сплайнов |
| io | Ввод и вывод |
| linalg | Линейная алгебра |
| ndimage | N-размерная обработка изображений |
| odr | Метод ортогональных расстояний |
| optimize | Оптимизация и численное решение уравнений |
| signal | Обработка сигналов |
| sparse | Разреженные матрицы |
| spatial | Разреженные структуры данных и алгоритмы |
| special | Специальные функции |
| stats | Статистические распределения и функции |
Подробное описание можно найти в официальной документации.
Эти пакеты нужно импортировать для использования библиотеки. Например:
Прежде чем рассматривать каждую функцию в подробностях, разберемся с теми из них, которые являются одинаковыми в NumPy и SciPy.
Видео:Метод Ньютона (метод касательных) Пример РешенияСкачать

Базовые функции
Взаимодействие с NumPy
SciPy построена на базе NumPy, поэтому можно использовать функции последней для работы с массивами. Чтобы узнать о них подробнее, используйте функции help() , info() или source() .
help():
Функция help() подойдет для получения информации о любой функции. Ее можно использовать двумя способами:
Вот пример для обоих:
При исполнении этого кода, первая help() вернет информацию о подмодуле cluster . А вторая — попросит пользователя ввести название модуля, ключевого слова и др., о чем требуется предоставить дополнительную информацию. Для выхода достаточно ввести quit и нажать Enter.
info():
Эта функция возвращает информацию о конкретных функциях, модулях и так далее.
source():
Исходный код можно получить только для тех объектов, которые были написаны на Python. Функция не вернет ничего важного, если методы или объекты были написаны, например, на C. Синтаксис простой:
Видео:Численное решение дифференциальных уравнений (задачи Коши)Скачать

Специальные функции
SciPy предоставляет набор специальных функций, используемых в математической физике: эллиптические настраиваемые функции, гамма, бета и так далее. Для их поиска нужно использовать функцию help() .
Экспоненциальные и тригонометрические функции
Набор специальных функций SciPy включает такие, с помощью которых можно искать экспоненты и решать тригонометрические задачи.
Есть и масса других функций из SciPy, с которым стоит познакомиться.
Видео:Решение ОДУ в PythonСкачать

Интегральные функции
Есть и функции для решения интегралов. В их числе как обычные дифференциальные интеграторы, так и методы трапеций.
В SciPy представлена функция quad , которая занимается вычислением интеграла функции с одной переменной. Границы могут быть ±∞ (± inf ) для обозначения бесконечных пределов. Синтаксис этой функции следующий:
А здесь она внедрена в пределах a и b (могут быть бесконечностями).
В этом примере функция a находится в пределах 0 и 1. После выполнения вывод будет такой:
Двойные интегральные функции
SciPy включает также и dblquad , которая используется для вычисления двойных интегралов. Двойной интеграл, как известно, состоит из двух реальных переменных. Функция dblquad() принимает функцию, которую нужно интегрировать, в качестве параметра, а также 4 переменных: две границы и функции dy и dx .
В SciPy есть другие функции для вычисления тройных интегралов, n интегралов, интегралов Ромберга и других. О них можно узнать подробнее с помощью help .
Функции оптимизации
В scipy.optimize есть часто используемые алгоритмы оптимизации:
Функция Розенброка
Функция Розенброка ( rosen ) — это тестовая проблема для оптимизационных алгоритмов, основанных на градиентах. В SciPy она определена следующим образом:
Nelder-Mead
Это числовой метод, который часто используется для поиска минимума/максимума функции в многомерном пространстве. В следующем примере метод использован вместе с алгоритмом Нелдера — Мида.
Видео:Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

Функции интерполяции
В сфере числового анализа интерполяция — это построение новых точек данных на основе известных. Библиотека SciPy включает подпакет scipy.interpolate, состоящий из сплайновых функций и классов, одно- и многомерных интерполяционных классов и так далее.
Одномерная интерполяция
Одномерная интерполяция — это область построения кривой, которая бы полностью соответствовала набору двумерных точек данных. В SciPy есть функция interp1d , которая используется для создания одномерной интерполяции.
Вывод:
Многомерная интерполяция
Многомерная интерполяция (пространственная интерполяция) — это тип интерполяции функций, который состоит из более чем одной переменной. Следующий пример демонстрирует работу функции interp2a .
При интерполяции на двумерную сетку функция использует массивы x, y и z для приближения функции f: «z = f(x, y)» и возвращает функцию, у которой вызываемый метод использует сплайновую интерполяцию для поиска значения новых точек.
Вывод:
Видео:МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

Функции преобразования Фурье
Анализ Фурье — это метод, который помогает представлять функцию в виде суммы периодических компонентов и восстанавливать сигнал из них. Функции fft используются для получения дискретной трансформации Фурье реальной или комплексной последовательности.
Похожим образом можно найти обратное значение с помощью функции ifft .
Видео:5 Численное решение дифференциальных уравнений Part 1Скачать

Функции обработки сигналов
Обработка сигналов — это область анализа, модификации и синтеза сигналов: звуков, изображений и т. д. SciPy предоставляет некоторые функции, с помощью которых можно проектировать, фильтровать и интерполировать одномерные и двумерные данные.
Фильтрация:
Фильтруя сигнал, можно удалить нежелаемые составляющие. Для выполнения упорядоченной фильтрации используется функция order_filter . Она выполняет операцию на массиве. Синтаксис следующий:
a — N-мерный массив с входящими данными
domain — массив масок с тем же количеством размерностей, что и у массива a
rank — неотрицательное число, которое выбирает элементы из отсортированного списка (0, 1…)
Сигналы
Подпакет scipy.signal также состоит из функций, с помощью которых можно генерировать сигналы. Одна из таких — chirp . Она является генератором частотно-модулированного сигнала, а ее синтаксис следующий:
Вывод:
Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Линейная алгебра
Линейная алгебра работает с линейными уравнениями и их представлениями с помощью векторных пространств и матриц. SciPy построена на базе библиотек ATLAS LAPACK и BLAS и является очень быстрой в сфере решения проблем, связанных с линейной алгеброй. В дополнение к функциям из numpy.linalg scipy.linalg также предоставляет набор продвинутых функций. Если numpy.linalg не используется вместе с ATLAS LAPACK и BLAS, то scipy.linalg работает намного быстрее.
Нахождение обратной матрицы
С математической точки зрения обратная матрица A — это матрица B, где AB = I, а I — это единичная матрица, состоящая из единиц по диагонали. Это можно обозначить как B=A-1. В SciPy такого можно добиться с помощью метода linalg.inv .
Нахождение определителей
Значение, полученное арифметическим путем из коэффициентов матрицы является определителем квадратной матрицы. В SciPy это делается с помощью функции det с таким синтаксисом:
det(a, overwrite_a=False, check_finite=True)
a — (M, M) — это квадратная матрица
overwrite_a(bool, optional) — разрешает перезаписывать данные
check_finite(bool, optional) — для проверки состоит ли матрица только из конечных чисел
Разреженные собственные значения
Разреженные собственные значения — это набор скаляров, связанных с линейными уравнениями. ARPACK предоставляет способ быстрого нахождения этих значений (собственных векторов). Вся функциональность скрыта в двух интерфейсах: scipy.sparse.linalg.eigs и scipy.sparse.linalg.eigsh .
Интерфейс eigs позволяет находить собственные значения реальных или комплексных несимметричных квадратных матриц, а eigsh содержит интерфейсы реальных симметричных или комплексных Эрмитовых матриц.
Функция eigh решает обобщенную проблему собственного значения для комплексной Эрмитовой или реально симметричной матрицы
Разреженные структуры данных и алгоритмы
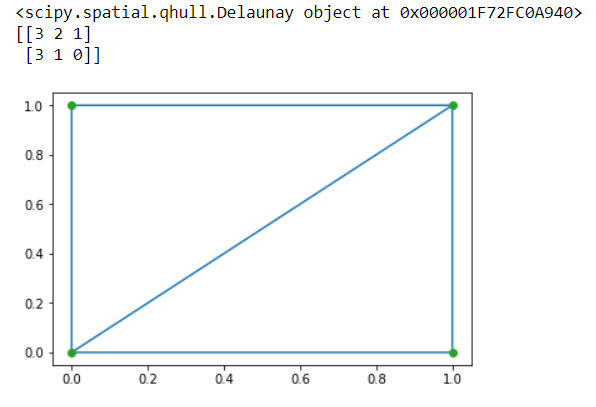
Разреженные данные состоят из объектов, которые в свою очередь состоят из линий, точек, поверхностей и так далее. Пакет scipy.spatial из SciPy может вычислять диаграммы Вороного, триангуляцию и другое с помощью библиотеки Qhull. Он также включает реализации KDTree для точечных запросов ближайших соседей.
Триангуляции Делоне
С математической точки зрения триангуляции Делоне для набора дискретных точек на плоской поверхности — это триангуляция, где ни одна точка из представленных не расположена внутри описанной окружности любого треугольника.
Вывод:
Функции многомерной обработки изображений
Обработка изображений — это выполнение операций над изображением по получению информации или улучшенной копии этого изображения из оригинала. Пакет scipy.ndimage состоит из нескольких функций обработки и анализа изображений, которые нужны для работы с массивами с произвольной размерностью.
Свертка и корреляция
В SciPy есть несколько функций для свертки и корреляции изображений.
- Функция correlate1d используется для вычисления одномерной корреляции по заданной оси
- Функция correlate предлагает многомерную корреляцию для любого массива с определенным ядром
- Функция convolve1d используется для вычисления одномерной свертки вдоль заданной оси
- Функция convolve предлагает многомерную свертку для любого массива с определенным ядром
Файловый ввод/вывод
Пакет scipy.io предоставляет несколько функций, которые помогают управлять файлами в разных форматах, включая MATLAB, файлы IDL, Matrix Market и другие.
Для использования его нужно сначала импортировать:
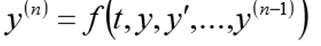
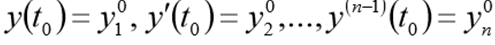


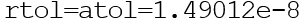
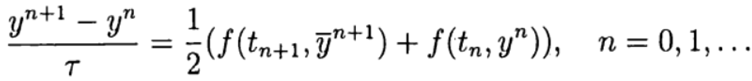
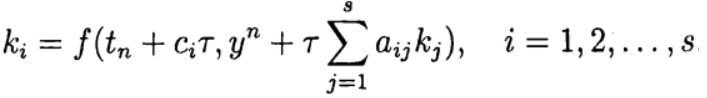
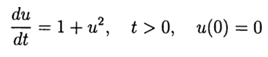 с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга
с использованием обеих функций def odein(),def oden() модуля scipy.integrate и адаптированного к Python методов Рунге—Кутта и Рунге—Кутта— Фельберга