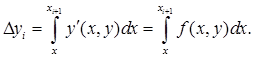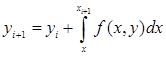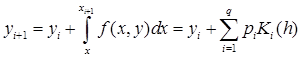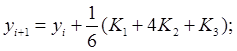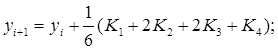Численное решение дифференциальных уравнений delphi (6 видео)

Об автоматическом дифференцировании, методе Ньютона и решении СЛАУ на Delphi. Часть 1

Об автоматическом дифференцировании (АД) на Хабре уже писалось здесь и здесь. В данной статье предлагается реализация АД для Delphi (протестировано в Embarcadero XE2, XE6) вместе с удобными классами методов Ньютона для решения нелинейных уравнений f(x) = 0 и систем F(X) = 0. Любые ссылки на готовые аналогичные библиотеки приветствуются, сам же я подобного не нашел, не считая отличного решателя СЛАУ с разреженной матрицей (см. под катом).

Давайте в самом начале отметим для себя, что выбор Delphi обусловлен legacy-кодом, тем не менее на C++ задачу можно решать следующим образом. Во-первых, для методов Ньютоновского (базовый метод Ньютона, метод Бройдена) типа имеются Numerical Recipes in C++. Ранее «Рецепты» были только на чистом C и приходилось делать свои классовые обертки. Во-вторых, можно взять одну из АД-библиотек из списка Autodiff.org. По моему опыту использования CPPAD быстрее FADBAD и Trilinos::Sacado примерно на 30%, самая же быстрая, судя по описанию, библиотека это новая ADEPT. В-третьих, для матрично-векторных операций можно взять проверенный временем uBlas , либо новые и быстрые конкуренты Armadillo и blaze-lib — это если для решения СЛАУ использовать отдельные библиотеки (например, SuiteSparce или Pardiso для прямых и ITL для итерационных методов). Привлекательным является также использование интегрированных библиотек линейной алгебры и решателей СЛАУ Eigen, MTL, PETSc (имеются также Ньютоновские решатели на C). Вся триада из заголовка полностью реализована, насколько мне известно, только в Trilinos.

Содержание

О применении численного дифференцирования
Реализация АД
Пример 1
Реализация АД для разреженных матриц
Пример 2
Курсовая работа: Программа для решения дифференциальных уравнений первого порядка методом Рунге-Кутта
Метод Рунге-Кутта решения дифференциальных уравнений и их систем
Метод Рунге-Кутта решения дифференциальных уравнений и их систем
🔥 Видео

Видео:Урок №1: Условия в Delphi - оператор "If Then" на примере программы "Решение квадратного уравнения"Скачать

О применении численного дифференцирования

Производные можно вычислять аналитически и численно. К аналитическим методам относятся ручное дифференцирование, символьное (Maple, Wolfram и т.п.) и непосредственно автоматическое дифференцирование, выраженное в средствах выбранного языка программирования.

Современный тренд на использование АД оправдан одной простой причиной — с помощью этой техники устраняется избыточность кода и его дублирование. Другой аргумент состоит в том, что, например, при решении нелинейных дифференциальных уравнений (систем) сеточными методами способ вычисления F(X) сам по себе является нетривиальной задачей. В реальных задачах невязка F(X) представлена суперпозицией вызовов функций с разных слоев программы и ручное дифференцирование теряет свою наглядность. Следует также отметить, что при моделировании нестационарных процессов F(X) меняется на каждом шаге по времени, также может меняться и сам вектор неизвестных X. Использование АД позволяет нам сконцентрироваться непосредственно на формировании F(X), однако не снимает вопрос о верификации получаемой матрицы Якобиана dF(X)/dX. Дело в том, что при вычислении невязок мы можем забыть изменить тип промежуточной переменной со стандартного double на тип АД (а многие библиотеки имеют неявное приведение типа АД к double), тем самым некоторые производные будут вычислены некорректно. Проблема в этом случае состоит в том, что даже при наличии ошибок в формулах для производных метод Ньютона может сходиться, хоть и за возросшее число итераций. Это может быть незаметно при одних начальных данных и приводить к расходимости процесса при других.

Таким образом, какой бы аналитической способ дифференцирования df/dx не был выбран, его крайне желательно дополнить сравнением с численным дифференцированием (f(x + h) — f(x)) / h, иначе всегда будут оставаться сомнения в правильности кода. Естественно, численные производные никогда не совпадут с точностью с правильными аналитическими, тем не менее можно порекомендовать следующий прием юнит-тестирования. Можно выгрузить в текстовые файлы вектора X, F(X) и матрицу dF(X)/dX и выложить на SVN. Затем получить dF(X)/dX численно и сохранить файл поверх существующего, после чего визуально сравнивать файлы между собой. Здесь Вы всегда увидите насколько поменялись значения и сможете локализовать координаты элементов матрицы с большими отклонениями (не в долях) — в этом месте находится ошибка аналитического дифференцирования.

Видео:5 Численное решение дифференциальных уравнений Part 1Скачать

Реализация АД

В Embarcadero Delphi до версии XE5 отсутствует возможность перегрузки арифметических операций для классов, но есть такая возможность для структур record (ссылка):

Обычно в АД на C++ размерность вектора производных является переменной величиной и инициализируется в конструкторе. В Delphi нельзя (есть попытки обойти) перегрузить оператор присваивания для структур и в связи с побитовым копированием вектор производных приходится делать фиксированной длины. Соответствующая константа TAutoDiff.n_all должна изначально задаваться вручную.

Пример 1

На данный момент в библиотеке перегружены почти все бинарные и унарные операторы, за исключением тригонометрических функций и булевых операций сдвига. Недостающие функции легко доработать самостоятельно.

Видео:5 Численное решение дифференциальных уравнений Part 1Скачать

Реализация АД для разреженных матриц

С одной стороны фиксированное значение n_all это существенное ограничение, ведь размерность вектора может поступать извне. С другой стороны для некоторых задач его можно ослабить. Дело в том, что если говорить о численных методах решения уравнений механики сплошных сред, то возникающие в них матрицы имеют разреженную структуру — классический пример это «схема крест» для оператора Лапласа, когда в уравнении для узла с координатами (i, j) (ограничимся 2D) задействованы только 5 узлов: (i, j), (i-1, j), (i+1, j), (i, j-1), (i, j+1). Обобщая идею мы должны заложить следующее для данной конкретной задачи:

Пусть общее число узлов в решаемой задаче N. Тогда в матрице Якобиана N_all = N * n_junc_vars столбцов, из них ненулевых только n_all. Если завести теперь внутри структуры TAutoDiff целочисленный вектор n_juncs, каждый элемент которого определяет глобальный индекс узла от 0 до N-1, то функцию dx с локальным индексом из диапазона [0, n_all-1] можно дополнить функцией dx_global с уже глобальным индексом из диапазона [0, N_all-1]. Пример 2 иллюстрирует детали использования такого интерфейса, плюсы которого будут наиболее полно видны при реализации метода Ньютона ниже.

Пример 2

В следующей части планируется рассмотрение класса методов Ньютоновского типа, а также вопроса выбора разреженного решателя СЛАУ. Пока же предлагаю читателям:

попробовать написать АД на C++11 с использованием семантики перемещений: 1) это должно работать очень быстро; 2) можно будет обойтись перегрузкой операторов без expression templates; 3) это будет впервые.
идею для курсовой по реализации АД на Roslyn CTP: можно работать сразу с синтаксическим деревом, которое содержит всю информацию об арифметических выражениях в F(X).

Видео:Численное решение задачи Коши методом ЭйлераСкачать

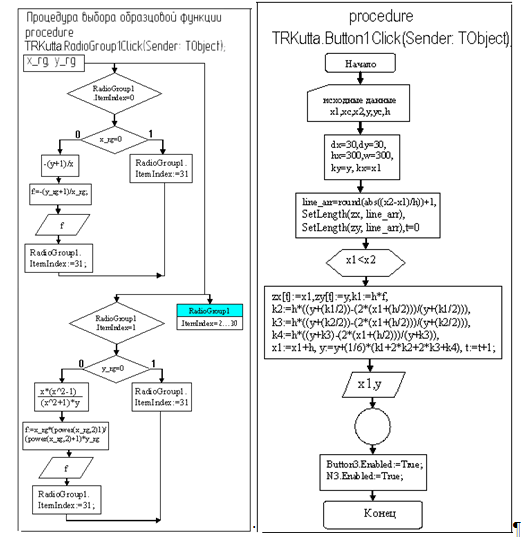
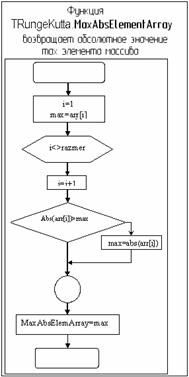
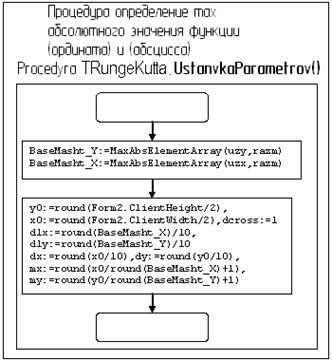
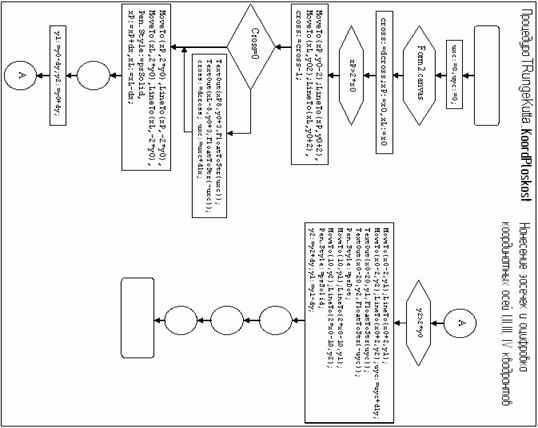
Курсовая работа: Программа для решения дифференциальных уравнений первого порядка методом Рунге-Кутта

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ

УКРАИНСКИЙ ГОСУДАРСТВЕННЫ Й

студент группы 3ИC27 Куделя С.В.

ассистент Ильхман Яна Викторовна

1. ОБЪЕКТНО-ОРИЕНТИРОВАННОЕ ПРОГРАММИРОВАНИЕ

2. ОПИСАНИЕ ПРЕДМЕТНОЙ ОБЛАСТИ (ПО)

2.1 Назначение программного продукта

2.2 Основные задачи

2.3 Входные и выходные данные

3.1 Выделение основных объектов ПО

3.2 Описание полей и методов

3.3 Иерархия классов на основе выделенных объектов

4. ОСНОВНЫЕ ФОРМЫ И КОМПОНЕНТЫ, ИСПОЛЬЗУЕМЫЕ ДЛЯ РЕАЛИЗАЦИИ ПРОГРАММЫ. ОСНОВНЫЕ АЛГОРИТМИЧЕСКИЕ РЕШЕНИЯ РЕЗУЛЬТАТЫ РАБОТЫ ПРОГРАММЫ

4.1 Метод Рунге-Кутта

4.2 Описание программы ” РЕШЕНИЕ ОДУ “

4.3 Назначение элементов графического окна программы

4.4 Реакция программы при возникновении ошибок

4.5 Перечень компонент DELPHI использованных в программе

5. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ И ТРЕБОВАНИЯ К ПО

6. ТЕКСТ ПРОГРАММЫ

7. РЕШЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ Y = Y−2X/Y МЕТОДОМ РУНГЕ – КУТТА В СРЕДЕ EXCEL

1. ОБЪЕКТНО-ОРИЕНТИРОВАННОЕ ПРОГРАММИРОВАНИЕ

Delphi является объектно-ориентированной средой программирования. В качестве языка программирования используется язык Object Pascal.

Исторически сложилось так, что программирование возникло и развивалось как процедурное программирование, которое предполагает, что основой программы является алгоритм, процедура обработки данных.

Объектно-ориентированное программирование (ООП) — это методика разработки программ, в основе которой лежит понятие объект. Объект — это некоторая структура, соответствующая объекту реального мира, его поведению. Задача, решаемая с использованием методики ООП, описывается в терминах объектов и операций над ними, а программа при таком подходе представляет собой набор объектов и связей между ними. Объектно-ориентированное программирование позволяет конструировать новые и производные (дочерние) классы на основе существующих классов.

По сравнению с традиционными способами программирования ООП обладает рядом преимуществ. Главное из них заключается в том, что эта концепция в наибольшей степени соответствует внутренней логике функционирования операционной системы (ОС) Windows. Программа, состоящая из отдельных объектов, отлично приспособлена к реагированию на события, происходящие в ОС. К другим преимуществам ООП можно отнести большую надежность кода и возможность повторного использования отработанных объектов.

Основные понятия ООП в языке Delphi: объект, класс, компонент;

Основные механизмы ООП: инкапсуляция, наследование и полиморфизм;

Класс — помимо описания данных, включает описание процедур и функций, которые могут быть выполнены над представителем класса — объектом. Данные класса называются полями, процедуры и функции — методами. Переменные в зависимости от предназначения именуются полями или свойствами.

При создании объекта он наследует структуру (переменные) и поведение (методы) своего класса.

Класс, называемый потомком, производным или дочерним классом (подклассом), также может быть создан на основе другого родительского класса (предка) и при этом наследует его структуру и поведение.

Методы — это процедуры и функции, описанные внутри класса и предназначенные для операций над его полями. В состав класса входит указатель на специальную таблицу, где содержится вся информация, нужная для вызова методов. От обычных процедур и функций методы отличаются тем, что им при вызове передается указатель на тот объект, который их вызвал. Поэтому обрабатываться будут поля именно того объекта, который вызвал метод. Внутри метода указатель на вызвавший его объект доступен под зарезервированным именем self.

Понятие свойства можно определить его как поле, доступное для чтения и записи не напрямую, а через соответствующие методы.

Классы могут быть описаны либо в секции интерфейса модуля, либо на верхнем уровне вложенности секции реализации. Не допускается описание классов внутри процедур и других блоков кода.

Любой компонент (элемент управления) или объект в Delphi всегда является экземпляром класса.

Программно объект представляет собой переменную объектного типа.

Для каждого компонента Delphi существует свой класс, наследуемый от TComponent. Предком всех объектов, включая компоненты, является класс TObject.

Инкапсуляция — это создание защищенных объектов, доступ к свойствам и методам которых разрешен только через определенные разработчиком . Иначе говоря, инкапсуляция — это предоставление разработчику конкретного набора свойств и методов для управления поведением и свойствами объекта, определяемыми внутри класса.

Инкапсуляция обеспечивает скрытие полей объекта с целью обеспечения доступа к ним только посредством методов класса.

В языке Delphi ограничение доступа к полям объекта реализуется при помощи свойств объекта. Свойство объекта характеризуется полем, сохраняющим значение свойства, и двумя методами, обеспечивающими доступ к полю свойства. Метод установки значения свойства называется методом записи свойства (write), а метод получения значения свойства — методом чтения свойства (read).

В описании класса перед именем свойства записывают слово property (свойство). Ключевое слово property обозначает свойство объекта, которое в отличие от обычных полей (переменных) класса имеет спецификаторы доступа обеспечивающие контроль доступа к свойствам объекта.

После имени свойства указывается его тип, затем — имена методов, обеспечивающих доступ к значению свойства. После слова read указывается имя метода, обеспечивающего чтение свойства, после слова write — имя метода, отвечающего за запись свойства.

Пример описания класса TPerson, содержащего два свойства: Name и Address:

TName = string [15]; TAddress = string[35];

TPerson = class // класс

FName: TName; // значениесвойства Name

FAddress: TAddress; // значениесвойства Address

Function GetName: TName;

Function GetAddress: TAddress;

Property Name: Tname // свойство Name

read GetName; // доступно только для чтения

Property Address: TAddress // свойство Address

read GetAddress // доступнодлячтения

write SetAddress; // изаписи

В программе для установки значения свойства записать обычную инструкцию присваивания значения свойству. Например, чтобы присвоить значение свойству Address объекта student, достаточно записать

student.Address := ‘Гвардейский, ул.Зенитная 1, кв.10’;

Внешне применение свойств ничем не отличается от использования полей объекта. Однако между свойством и полем объекта существует принципиальное отличие: при присвоении и чтении значения свойства автоматически вызывается процедура, которая выполняет некоторую работу.

Наследование позволяет определять новые классы в терминах существующих классов.

Новые классы возможно определять посредством добавления полей, свойств и методов к уже существующим классам. Такой механизм получения новых классов называется порождением. При этом новый, порожденный класс (потомок) наследует свойства и методы своего базового, родительского класса.

В объявлении класса-потомка указывается класс родителя. Например, класс TEmployee (сотрудник) может быть порожден от рассмотренного выше класса TPerson путем добавления поля FDepartment (отдел). Объявление класса TEmplioyee в этом случае может выглядеть так:

TEmployee = class (TPerson)

FDepartment: integer; // номеротдела

constructor Create(Name:TName; Dep:integer);

Заключенное в скобки имя класса TPerson показывает, что класс TEmployee является производным от класса TPerson. В свою очередь, класс TPerson является базовым для класса TEmployee.

Класс TEmpioyee должен иметь свой собственный конструктор, обеспечивающий инициализацию класса-родителя и своих полей.

Пример реализации конструктора класса TEmployee:

В приведенном примере директивой inherited вызывается конструктор родительского класса. После этого присваивается значение полю класса-потомка.

После создания объекта производного класса в программе можно использовать поля и методы родительского класса. Ниже приведен фрагмент программы, демонстрирующий эту возможность.

engineer.address := ‘ул.Блохина, д.8, кв.10’;

Первая инструкция создает объект типа TEmployee, вторая — устанавливает значение свойства, которое относится к родительскому классу.

Полиморфизм — это возможность различных объектов реагировать по-разному на одни и те же события, иначе говоря, возможность использовать одинаковые имена для методов, входящих в различные классы. Концепция полиморфизма обеспечивает в случае применения метода к объекту использование именно того метода, который соответствует классу объекта. Синтаксис языка поддерживает общепринятую для объектно-ориентированного программирования нотацию: имя_объекта: свойство для ссылки на свойство объекта или имя_объекта: метод для вызова метода объекта. При этом имя_объекта может содержать как простую, так и квалифицированную ссылку. Квалифицированная ссылка содержит отделенные точкой имена родительских объектов.

Пусть определены три класса, один из которых является базовым для двух других:

// базовыйкласс TPerson = class

fname: string; // имя

function info: string;

// производныйот TPerson TStud = class(TPerson)

constructor Create(name:string; gr:integer);

function info: string; override; end;

// производныйот TPerson TProf = class(TPerson)

function info: string;

В каждом из этих классов определен метод info. В базовом классе при помощи директивы virtual метод info объявлен виртуальным. Объявление метода виртуальным дает возможность дочернему классу произвести замену виртуального метода своим собственным. В каждом дочернем классе определен свой метод info, который замещает соответствующий метод родительского класса (метод порожденного класса, замещающий виртуальный метод родительского класса, помечается директивой override).

Определение метода info для каждого класса:

result := fname + ‘ гp.’ + IntTostr(fgr);

result := fname + ‘ каф.’ + fdep;

Так как оба класса порождены от одного и того же базового, объявить список студентов и преподавателей можно так (следует помнить, что объект — это указатель):

list: array [l. .SZL] of TPerson;

Объявить подобным образом список можно потому, что язык Delphi позволяет указателю на родительский класс присвоить значение указателя на дочерний класс. Поэтому элементами массива list могут быть как объекты класса TStud, так и объекты класса TProf.

Вывести список студентов и преподавателей можно применением метода info к элементам массива. Например, так:

for i:=l to SZL do // SZL — размер массива-списка

then st := st + list[i].Info

+ #13; ShowMessage (st);

Во время работы программы каждый элемент массива может содержать как объект типа xstud, так и объект типа TProf. Концепция полиморфизма обеспечивает применение к объекту именно того метода, который соответствует типу объекта.

Есть еще одна, совершенно особенная разновидность методов — перегружаемые.

Перегрузка методов нужна, чтобы произвести одинаковые или похожие действия с разнотипными данными.

Пример, иллюстрирующий статические методы:

procedure SetData(AValue: Extended);

procedure SetData(AValue: Integer); end;

В этом случае попытка вызова из объекта Т2 методов

вызовет ошибку компиляции на первой из двух строк. Для компилятора внутри Т2 статический метод с параметром типа extended перекрыт, и он его «не признает».

Для выхода из сложившегося положения можно переименовать один из методов, например, создать SetlntegerData и SetExtendedData, но если методов не два, а, например, сто, моментально возникнет путаница. Сделать методы виртуальными нельзя, поскольку тип и количество параметров в одноименных виртуальных методах должны в точности совпадать. Для разрешения этой ситуации существуют перегружаемые методы, объявляемые при помощи директивы overload:

procedure SetData(AValue: Extended);overload;

procedure SetData(AValue: Integer); overload;

Объявив метод SetData перегружаемым, в программе можно использовать обе его реализации одновременно. Это возможно потому, что компилятор определяет тип передаваемого параметра (целый или с плавающей точкой) и в зависимости от этого подставит вызов соответствующего метода: для целочисленных данных — метод объекта T2ndobj, для данных с плавающей точкой — метод объекта Tistobj.

Можно перегрузить и виртуальный (динамический) метод. Надо только в этом случае добавить директиву reintroduce:

procedure SetData(AValue: Extended); overload; virtual;

procedure SetData(AValue: Integer); reintroduce; overload ;

На перегрузку методов накладывается ограничение — нельзя перегружать методы, находящиеся в области видимости published, т. е. те, которые будут использоваться в Инспекторе объектов.

В модели объектов языка Delphi существует механизм доступа к составным частям объекта, определяющий области, где ими можно пользоваться (области видимости). Поля и методы могут относиться к четырем группам (секциям), отличающимся областями видимости. Методы и свойства могут быть общими (секция public ), личными (секция private ), защищенными (секция protected ) и опубликованными (секция published ). Есть еще и пятая группа, automated , она ранее использовалась для создания объектов СОМ; теперь она присутствует в языке только для обратной совместимости с программами на Delphi версий 3—5.

Области видимости, определяемые первыми тремя директивами, таковы.

· Поля, свойства и методы секции public не имеют ограничений на видимость. Они доступны из других функций и методов объектов, как в данном модуле, так и во всех прочих, ссылающихся на него.

· Поля, свойства и методы, находящиеся в секции private , доступны только в методах класса и в функциях, содержащихся в том же модуле, что и описываемый класс. Такая директива позволяет полностью скрыть детали внутренней реализации класса. Свойства и методы из секции private можно изменять, и это не будет сказываться на программах, работающих с объектами этого класса. Единственный способ для кого-то другого обратиться к ним — переписать заново созданный вами модуль (если, конечно, доступны исходные тексты).

· Поля, свойства и методы секции protected также доступны только внутри модуля с описываемым классом. Но — и это главное — они доступны в классах, являющихся потомками данного класса, в том числе и в других модулях. Такие элементы особенно необходимы для разработчиков новых компонентов — потомков уже существующих. Оставляя свободу модернизации класса, они все же скрывают детали реализации от того, кто только пользуется объектами этого класса.

СОЗДАНИЕ НОВОГО КЛАССА

Для того чтобы создать новый класс, в interface-секции кода модуля следует записать:

Каждая форма в проекте, разрабатываемом в Delphi, описывается отдельным модулем (создаваемым автоматически при создании новой формы). Этот модуль описывает новый класс для компонента Form. Первоначально по умолчанию создается класс TForml, наследуемый от класса TForm из VCL-библиотеки. Это автоматически записывается в модуле следующим образом:

type (Объявление класса>

[Объявление private переменных и методов>

Объявление переменных и методов класса

Переменные класса указываются после модификаторов доступа (public, private , protected, published, automated ), определяющих их область видимости. Свойства, указанные после модификатора доступа published, являются общедоступными и отображаются в инспекторе объектов.

После имени переменной или списка имен, разделенных через запятую, указывается символ : и тип переменной. Типом может быть как базовый тип Delphi (например. Integer, Boolean), так и производный тип, в том числе реализуемый, как некоторый класс. Такой тип иногда называется объектным типом.

При объявлении методов класса перед именем метода указывается ключевое слово function или procedure. Для функций также после имени функции через символ указывается тип возвращаемого значения.

Var2, Var3: TVarTypeClass;

function F1: Integer;

Объявление класса содержит только объявление переменных и методов. Реализация методов — функций и процедур — записывается в implementation-секции модуля.

Каждый модуль, создаваемый на основе разрабатываемой формы, представляет собой описание класса. Как правило, производного от класса TForm. Любой компонент, располагаемый в форме, также является экземпляром некоторого класса.

Классы в Delphi образуют иерархическое дерево. Будем называть классы из VCL-библиотеки Delphi базовыми классами. Иерархическое дерево для некоторого класса любого компонента имеет корневым элементом класс TObject. Просмотреть иерархию классов-потомков можно в окне Exploring. Для того чтобы перейти в него, достаточно выполнить команду меню View|Browser или нажать клавиши Shift+CtrL+B.

На рис.1 представлена страница Classes окна Exploring Classes. На ней отображено иерархическое дерево наследования для класса TForm 1. В правой части окна расположена панель, содержащая три страницы — Scope, Inheritance, References. Страница Scope содержит древовидную диаграмму всех объектов, переменных и методов выделенного на левой панели класса. При этом ветвь Inherited содержит имена класса-предка и класса-потомка. Страница Inheritance содержит поддерево иерархии классов, начиная с класса-предка для выделенного на левой панели класса.

На странице References можно узнать имена всех модулей и номера строк, в которых встречается имя данного класса.

Для того чтобы добавить в проект собственные описания производных классов, наиболее целесообразно создать отдельный модуль и в interface-секции модуля записать все объявления классов.

Все классы VCL-библиотеки Delphi разбиты на группы, которые расположены в каталоге Delphi7SourceVCL . Для того чтобы просмотреть файл библиотеки, достаточно выполнить File | Open и выбрать каталог и имя файла. Справа в окне кода программы (рис.2) будет показан код модуля, а слева — список всех объявленных в нем классов.

СВОЙСТВА / МЕТОДЫ И ОБРАБОТЧИКИ СОБЫТИЙ

Каждый объект обладает набором свойств. Свойства могут быть как наследуемые от родительского класса, так и добавленные индивидуально для создаваемого объекта. Список всех свойств объекта и их значений отображается в диалоговом окне Object Inspector.

Ссылка на свойство в программном модуле записывается как

Метод — это процедура или функция, ассоциируемая с некоторым объектом.

Ссылка на методов программном модуле записывается как

Delphi-приложение выполняется в среде Windows, и как любое Windows-приложение, получает сообщения о возникающих для него событиях. Управление приложением фактически сводится к обработке получаемых сообщений.

Методы, в которых содержится код обработки события, называются обработчиками событий (Event Handler). Delphi автоматически генерирует процедуры обработки событий – обработчикисобытий для любого компонента. При этом имя обработчика событий формируется из имени компонента и названия события (например, EditlClick). Имя обработчика события автоматически квалифицируется именем класса формы.

Например: TForml.ButtonlClick(Sender: TObject);.

Для каждого компонента предусмотрено одно стандартное событие. Например, для командной кнопки, флажка, списка, поля ввода — это событие Click, а для формы — событие FormCreate.

Для того чтобы автоматически добавить в модуль объявление и описание обработчика стандартного события, достаточно выполнить на компоненте формы или самой форме двойной щелчок мышью. Объявление события добавляется в interface-секцию модуля, а пустое описание события — в implementation-секцию модуля. Далее в редакторе кода внутри уже имеющегося блока begin end; следует только ввести код обработчика события.

procedure TForml.ButtonlClick(Sender: TObject);

Для того чтобы добавить обработчик любого события, можно выбрать в инспекторе объектов страницу Events и выполнить двойной щелчок мышью в поле, расположенном справа от имени события. Это поле представляет собой комбинированное окно списка — в него можно вводить новое значение имени обработчика события двойным щелчком мыши или выбирать имя уже существующей процедуры. Это позволяет при необходимости определять одну процедуру обработки событий одновременно для нескольких событий.

2. ОПИСАНИЕ ПРЕДМЕТНОЙ ОБЛАСТИ (ПО)

2.1 Назначение программного продукта

Программа предназначена для решения заданных программно обыкновенных дифференциальных уравнений первого порядка методом Рунге – Кутта, вывода результата решения ОДУ на экран в виде графика в декартовой системе координат.

2.2 Основные задачи

Программа обеспечивает решение следующих задач:

− ввод исходных данных;

− решение ОДУ и вывод результата решения в численном и аналитическом виде;

− обнуление результатов решения ОДУ;

− контроль корректности ввода исходных данных и вывод на экран сообщение о содержании

ошибки с рекомендацией по её устранению;

− контроль возникновения в процессе вычислений ошибки «деление на ‘0’» и вывод на экран

соответствующего сообщения о содержании ошибки с рекомендацией по её устранению.

2.3 Входные и выходные данные

Входными данными для программы являются:

− начальное условие решения ОДУ − у'(х₀ ) = у₀ .,

− начальное и конечное значения отрезка, в пределах которого находится решение ОДУ;

−величина шага дифференцирования,

−формула образцовой функции.

Выходными данными программы являются:

− массив (х₁ ,у₁ ; х₂ ,у₂ ;…; х_i ,у_i ) − решений выбранного дифференциального уравнения на заданном

− график функции, которая, будучи подставленной, в исходное образцовое уравнение, обращает его в

тождество и одновременно удовлетворяет начальному условию.

3.1 Выделение основных объектов ПО

− Объект класса TRKutta (Form1) – главная окно программы.

− Объект класса TRngeKutta (Form2) – окно вывода графика функции-решения ДУ.

− Объект класса TSpravka(Form3) – окно «О программе».

− Объект класса TRungeKutta – координатная плоскость и график функции;

3.2 Описание полей и методов

x1 — значение x1(начало отрезка);

x2 — значение x2(конец отрезка);

yc — начальные значения (Y0) для передачи в графический модуль;

xc — начальные значения (х0)для передачи в графический модуль;

h– зачение величины шага вычислений;

f- значение функции при начальных условиях

zx — массив значений аргумента;

zy — массив значений функции;

line_arr — размерность массивa;

procedureButton1Click – вычисление значений функции – решения ОДУ;

procedureButton2Click – очистка полей ввода/вывода данных;

procedure Button3Click — выводокнаГРАФИК;

procedure Button4Click — выходизпрограммы;

procedure RadioGroup1Click — выборобразцовойфункции;

procedure Button5Click — активациявводаобразцовыхфункций;

procedure Button6Click — деактивациявводаобразцовыхфункций;

procedureN7Click — вывод информации о программе;

Класс TRungeKutta ( родительский классTObject )

x0,y0 — координаты начала координатных осей;

dx,dy- шаг координатной сетки (в пикселях)

y1,y2,xP,xL — засечки по оси Y и X

dlx,dly — шаг меток (оцифровки) линий сетки по X и Y

cross- счетчик неоцифрованных линий сетки

dcross- количество неоцифрованных линий между оцифрованными

razm– размер массивов;

uzx- Динамический массив координат-X

uzy- Динамический массив координат-Y

uxc,uyc — Оцифровка по осям

mx, my- масштабы по осям X и Y;

BaseMasht_X,BaseMasht_Y — МАХ значения элементов в массивах

functionMaxAbsElementArray– определяет MAX элемент массива по модулю;

procedureUstanovkaParametrov – вычисляет исходные параметры необходимые для построения декартовой плоскости;

procedureKoordPloskost – вычерчивает координатную плоскость;

constructorTRungeKutta.CreateGr — создание объекта (график функции, координатная сетка, координатные оси)

RungeKutta — переменная-объект классаTRungeKutta ;

procedureN4Click — вывод графика функции в окне ‘График’;

procedureN5Click — закрытие окна ‘График’;

procedureButton1Click – процедура вывода информации о программе

3.3 Иерархия классов на основе выделенных объектов

Название: Программа для решения дифференциальных уравнений первого порядка методом Рунге-Кутта
Раздел: Рефераты по информатике, программированию
Тип: курсовая работа Добавлен 21:04:57 05 апреля 2011 Похожие работы
Просмотров: 3135 Комментариев: 20 Оценило: 4 человек Средний балл: 5 Оценка: неизвестно Скачать

Численное решение дифференциальных уравнений delphi

1. Решение дифференциальных уравнений

Пусть дано дифференциальное уравнение первого порядка:

и начальное условие его решения:

Тогда решить уравнение — это значит найти такую функцию у — φ(х), которая, будучи подставленной, в исходное уравнение, обратит его в тождество и одновременно будет удовлетворено начальное условие. Задача отыскания функции у = φ (х) называется в математике задачей Коши. При решении дифференциального уравнения порядка nзадача Коши формулируется следующим образом.

Дано дифференциальное уравнение порядка n:

у ( n ) = f(x, y, у’ ’ ,…,y n -1 )

Необходимо найти такую функцию у = φ (х), которая, будучи подставленной в исходное уравнение, обратит его в тождество и одновременно будут удовлетворены следующие п начальных условий:

4.1 Метод Рунге-Кутта

Метод Рунге-Кутта обладает более высокой точностью, чем методы Эйлера за счет снижения методических ошибок. Идея метода состоит в следующем.

По методу Эйлера решение дифференциального уравнения первого порядка определяется из соотношения:

Тогда приращение Δ y_i , может быть найдено путем интегрирования:

Вычислим теперь интеграл по методу прямоугольников:

Из полученного выражения видно, что вычисление интеграла по методу прямоугольников приводит к формуле Эйлера.

Вычислим интеграл по формуле трапеций:

Из выражения видно, что оно совпадает с расчетной формулой усовершенствованного метода Эйлера-Коши. Для получения более точного решения дифференциального уравнения следует воспользоваться более точными методами вычисления интеграла. В методе Рунге-Кутта искомый интеграл представляется в виде следующей конечной суммы:

где Pi— некоторые числа, зависящие от q; K_i (h) — функции, зависящие от вида подынтегральной функции f(x,y) и шага интегрирования h, вычисляемые по следующим формулам:

Значения p, α, β получают из соображений высокой точности вычислений. Формулы Рунге-Кутта третьего порядка (q= 3) имеют следующий вид:

Наиболее часто используется метод Рунге-Кутта четвертого порядка, для которого расчетные формулы имеют следующий вид:

Формулы Рунге-Кутта имеют погрешности порядка h q +1 . Погрешность метода Рунге-Кутта четвертого порядка имеет порядок h 5

4.2 Описание программы ” РЕШЕНИЕ ОДУ “

Программа ”Решение ОДУ“ достаточно проста в использовании.

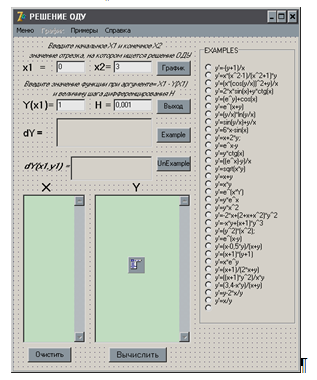
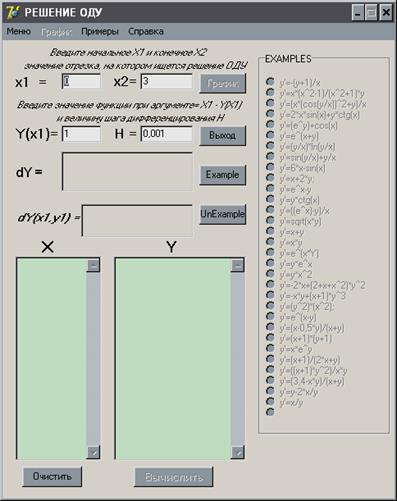
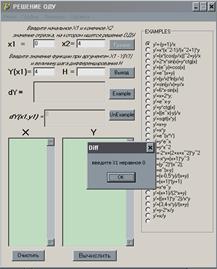
При запуске программы открывается главное окно программы (рис. 4 ), с установленными по умолчанию начальными условиями в полях ввода.

Назначение элементов ввода данных.

1. Поля X 1, X 2, Y ( x 1), H предназначены для ввода начального и конечного значений отрезка, на котором ищется решение дифференциального уравнения, значения функции при аргументе равном Х1 и величины шага дифференцирования;

2. В поле dY выводится формула дифференциального уравнения 1-й степени, выбранная для решения;

3. В поле dY ( x 1, y 1) выводится значение производной в исходной точке.

Назначение элементов управления и контроля.

1. При нажатии кнопки EXAMPLE активируются “радиокнопки” выбора уравнений;

2. Щелчком “радиокнопки” выбирается соответствующее ей уравнение, вид формулы контролируется по её отображению в поле dY ;

3. Щелчком по кнопке ВЫЧИСЛИТЬ находятся приближенные решения выбранного дифференциального уравнения на заданном интервале;

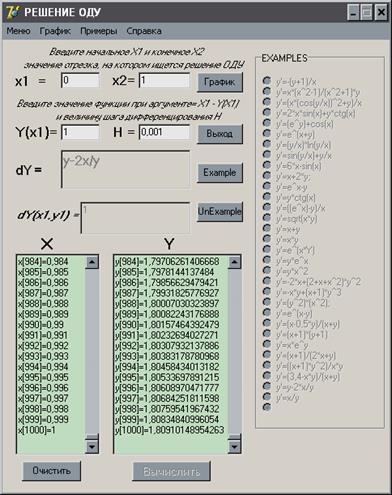
4. Решения дифференциального уравнения в виде пар значений X — Y выводятся в поля X и Y ; (рис. 5.)

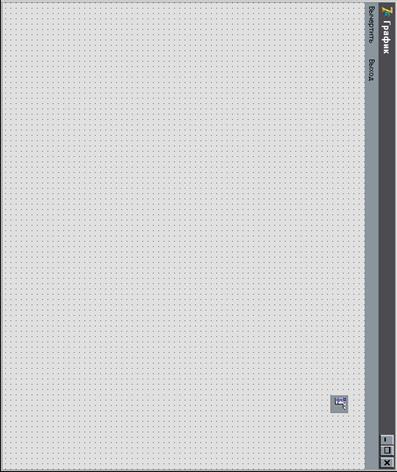
По окончании вычислений активируются кнопка ГРАФИК и пункт меню ГРАФИК главного окна системы.

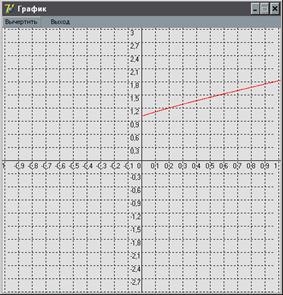
4.3 Назначение элементов графического окна программы

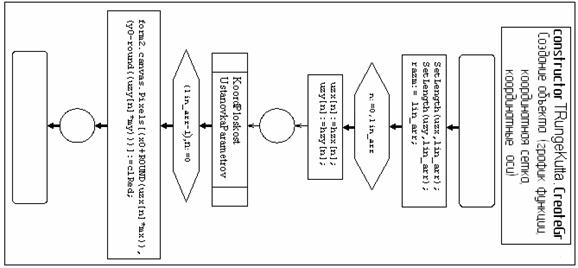
Вход в графическое окно осуществляется с помощью кнопок ГРАФИК наглавной формеили пункт меню ГРАФИК (рис. 6).

С помощью кнопки ВЫЧЕРТИТЬ на координатную плоскость выводится график функции – решение дифференциального уравнения на заданном интервале.

4.4 Реакция программы при возникновении ошибок

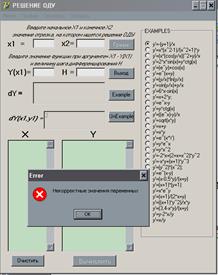
При вводе пользователем ошибочных данных (отсутствии начальных условий, некорректных значений переменных) программа выдает сообщение об ошибке (рис.7 а, б) рис.7 а. рис.7 б.

4.5 Перечень компонент DELPHI использованных в программе

В Form 1 использованы компоненты:

— Edit1.text, Edit2.text, Edit3.text, Edit4.text – для ввода начальных условий дифференциального

— Memo4.TMemo – для вывода формулы уравнения;

— Memo1.TMemo, Memo2.TMemo — для вывода результатов вычислений;

— Memo3.TMemo – для вывода значения производной в точке (Х0,Y0)

— ScrollBars ssVertical всвойствахMemo1.TMemo, Memo2.TMemo;

— Button1 “Вычислить”, Button2 “Очистить”, Button3 “График”, Button4 “Выход”,

Button5 “Example”, Button6 “UnExample”;

— Label1.TLabel — Label9.TLabel – дляотображенияназначениякомпонентов Memo иEdit;

— RadioGroup – для выбора вида уравнения;

В Form 2 использованы компоненты:

— MainMenu- для построения графика;

В Form 3 использованы компоненты:

— Panel1.TPanel – для размещения информации о программе;

— Label1.TLabel – Label14.TLabel – для отображения информации о программе;

— Button1.TButton “OK” – для выхода из окна

5. ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ И ТРЕБОВАНИЯ К ПО

Программа работает в среде операционных систем Windows 9х, NT.

Требования к ПО

Минимальные системные требования

aпроцессор Intel 486 с рабочей частотой 66 MHz и выше;

b) операционная система Windows 95, 98, NT 4.0, 2000, XP;

с) 16 Мбайт оперативной памяти (или более);

d) 3 Мбайт свободного пространства на жёстком диске.

6. ТЕКСТ ПРОГРАММЫ

Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,

StdCtrls, CheckLst, ComCtrls, ExtCtrls,math, Menus;

Видео:Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

Метод Рунге-Кутта решения дифференциальных уравнений и их систем

Delphi site: daily Delphi-news, documentation, articles, review, interview, computer humor.

Метод Рунге-Кутта решения дифференциальных уравнений и их систем

Метод позволяет решать системы обыкновенных дифференциальных уравнений (ОДУ) первого порядка следующего вида:
,
,
и т.д.,

которые имеют решение:

,
,
и т.д.,

где t – независимая переменная (например, время); X, Y и т.д. – искомые функции (зависимые от t переменные). Функции f, g и т.д. – заданы. Также предполагаются заданными и начальные условия, т.е. значения искомых функций в начальный момент.

Одно дифференциальное уравнение – частный случай системы с одним элементом. Поэтому, далее речь пойдет для определенности о системе уравнений.

Метод может быть полезен и для решения дифференциальных уравнений высшего (второго и т.д.) порядка, т.к. они могут быть представлены системой дифференциальных уравнений первого порядка.

Метод Рунге-Кутта заключается в рекурентном применении следующих формул:

.
где
,
,
,
,
,
,
,

Реализация Метода Рунге-Кутта на Delphi может выглядеть так (привожу полностью модуль):

type
TVarsArray = array of Extended; // вектор переменных включая независимую
TInitArray = array of Extended; // вектор начальных значений
TFunArray = array of function(VarsArray: TVarsArray ):Extended;
// вектор функций
TResArray = array of array of Extended; // матрица результатов
TCoefsArray = array of Extended; // вектор коэффициетов метода

function Runge_Kutt( // метод Рунге-Кутта
FunArray: TFunArray; // массив функций
First: Extended; // начальная точка по независимой координате
Last: Extended; // конечная точка по независимой координате
Steps: Integer; // число шагов по независимой координате
InitArray: TInitArray; // вектор начальных значений
var Res: TResArray // матрица результатов включая независ. переменную
):Word;
// возвращаемое значение — код ошибки

implementation
Function Runge_Kutt( // метод Рунге-Кутта
FunArray: TFunArray; // массив функций
First: Extended; // начальная точка по независимой координате
Last: Extended; // конечная точка по независимой координате
Steps: Integer; // число шагов по независимой координате
InitArray: TInitArray; // вектор начальных значений
var Res: TResArray // матрица результатов включая независ. переменную
):Word; // возвращаемое значение — код ошибки
var
Num: Word; // число уравнений
NumInit: Word; // число начальных условий
Delt: Extended; // шаг разбиения
Vars: TVarsArray; // вектор переменных включая независимую
Vars2,Vars3,Vars4: TVarsArray; // значения перем. для 2-4 коэф.
Coefs1: TCoefsArray; // вектор 1-ыx коэффициентов в методе
Coefs2: TCoefsArray; // вектор 2 коэффициентов в методе
Coefs3: TCoefsArray; // вектор 3 коэффициентов в методе
Coefs4: TCoefsArray; // вектор 4 коэффициентов в методе
I: Integer; // счетчик цикла по иттерациям
J: Word; // индекс коэф.-тов метода
K: Integer; // счетчик прочих циклов
begin
Num:=Length(FunArray); // узнаем число уравнений
NumInit:=Length(InitArray); // узнаем число начальных условий
If NumInitNum then
begin
Result:=100; // код ошибки 100: число уравнений не равно числу нач. усл.
Exit;
end;
Delt:=(Last-First)/Steps; // находим величину шага разбиений
SetLength(Res,Num+1,Steps+1); // задаем размер матрицы ответов с незав. перем.
SetLength(Vars,Num+1); // число переменных включая независимую
SetLength(Vars2,Num+1); // число переменных для 2-го коэф. включая независимую
SetLength(Vars3,Num+1); // число переменных для 3-го коэф. включая независимую
SetLength(Vars4,Num+1); // число переменных для 4-го коэф. включая независимую
SetLength(Coefs1,Num); // число 1-ыx коэф. метода по числу уравнений
SetLength(Coefs2,Num); // число 2-ыx коэф. метода по числу уравнений
SetLength(Coefs3,Num); // число 3-иx коэф. метода по числу уравнений
SetLength(Coefs4,Num); // число 4-ыx коэф. метода по числу уравнений
// Начальные значения переменных:
Vars[0]:=First;
For K:=0 to NumInit-1 do Vars[K+1]:=InitArray[K];
For J:=0 to Num do Res[J,0]:=Vars[J]; // первая точка результата
For I:=0 to Steps-1 do // начало цикла иттераций
begin
For J:=0 to Num-1 do Coefs1[J]:=FunArray[J](Vars)*delt; // 1-й коэфф.
// Находим значения переменных для второго коэф.
Vars2[0]:=Vars[0]+delt/2;
For K:=1 to Num do Vars2[K]:=Vars[K]+Coefs1[K-1]/2;
For J:=0 to Num-1 do Coefs2[J]:=FunArray[J](Vars2)*delt; // 2-й коэф.
// Находим значения переменных для третьго коэф.
Vars3[0]:=Vars[0]+delt/2;
For K:=1 to Num do Vars3[K]:=Vars[K]+Coefs2[K-1]/2;
For J:=0 to Num-1 do Coefs3[J]:=FunArray[J](Vars3)*delt; // 3 коэфф.
// Находим значения переменных для 4 коэф.
Vars4[0]:=Vars[0]+delt;
For K:=1 to Num do Vars4[K]:=Vars[K]+Coefs3[K-1];
For J:=0 to Num-1 do Coefs4[J]:=FunArray[J](Vars4)*delt; // 4 коэфф.
// Находим новые значения переменных включая независимую
Vars[0]:=Vars[0]+delt;
For K:=1 to Num do
Vars[K]:=Vars[K]+(1/6)*(Coefs1[K-1]+2*(Coefs2[K-1]+Coefs3[K-1])+Coefs4[K-1]);
// Результат иттерации:
For J:=0 to Num do Res[J,I+1]:=Vars[J];
end; // конец итераций
Result:=0; // код ошибки 0 — нет ошибок
end;

Модуль полностью работоспособен. Возвращаемое функцией Runge_Kutt значение – код ошибки. Вы можете дополнить список ошибок по своему усмотрению. Рассчитанные функции системы помещаются в массив Res. Чтобы не загромождать код, в модуле опущены проверки (типа блоков try). Рекомендую их добавить по своему усмотрению.

Ниже приводится описание функции Runge_Kutt и типов, использующихся в модуле.

Function Runge_Kutt (FunArray: TFunArray; First: Extended; Last: Extended; Steps: Integer; InitArray: TInitArray; var Res: TResArray):Word;

Здесь:
FunArray — вектор функций (правых частей уравнений системы);
First, Last — начальная и конечная точки расчетного интервала;
Steps — число шагов по расчетному интервалу;
InitArray — вектор начальных значений
Res — матрица результатов включая независимую переменную.

В модуле описаны типы:

type
TVarsArray = array of Extended; // вектор переменных включая независимую
TInitArray = array of Extended; // вектор начальных значений
TFunArray = array of function(VarsArray: TVarsArray ):Extended; // вектор функций
TResArray = array of array of Extended; // матрица результатов
TCoefsArray = array of Extended; // вектор коэффициетов метода

Функция возвращает коды ошибок:
0 – нет ошибок;
100 — число уравнений не равно числу начальных условий.

Решение содержится в переменной-матрице Res. Первый индекс матрицы относится к переменной (0 – независимая переменная, 1 – первая зависимая и т.д.), второй – к номеру расчетной точки (0 – начальная точка).

Рассмотрим один пример использования модуля. Создадим новое приложение и подключим к нему модуль. На форме приложения разместим кнопку Button1 и область текста Memo1. Поместим в приложение две функции и обработчик нажатия кнопки:

//Задаем функции (правые части уравнений)
function f0(VarArray:TVarsArray):extended;
begin
Result:=4*VarArray[0]*VarArray[0]*VarArray[0];
end;

function f1(VarArray:TVarsArray):extended;
begin
Result:=1;
end;

procedure TForm1.Button1Click(Sender: TObject);
var
I: Integer;
FunArray: TFunArray; // массив функций
First: Extended; // начальная точка по независимой координате
Last: Extended; // конечная точка по независимой координате
Steps: Integer; // число шагов по независимой координате
InitArray: TInitArray; // вектор начальных значений
Res: TResArray; // матрица результатов включая независ. переменную
begin // Создаем вектор функций:
SetLength(FunArray,2);
FunArray[0]:=f0;
FunArray[1]:=f1;
// Задаем интервал и число шагов:
First:=0;
Last:=10;
Steps:=10;
// Задаем начальные условия:
SetLength(InitArray,2);
InitArray[0]:=0;
InitArray[1]:=0;
// Вызов метода и получение результатов:
Memo1.Lines.Clear;
I:=Runge_Kutt(FunArray, First, Last, Steps, InitArray, Res);
ShowMessage(‘Код ошибки = ‘+IntToStr(I));
For I:=0 to Steps do
Memo1.Lines.Add(floattostr(Res[0,I])+’ ‘+floattostr(Res[1,I])+’ ‘+floattostr(Res[2,I]));
end;