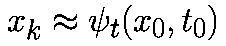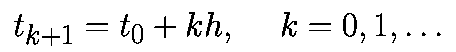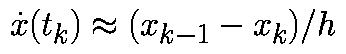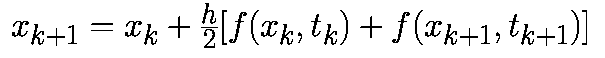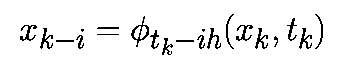Численное интегрирование системы дифференциальных уравнений явный и неявный методы эйлера

Дата добавления: 2015-06-12 ; просмотров: 15300 ; Нарушение авторских прав

Процесс формирования математической модели для численного интегрирования обязательно включает этап алгебраизации, который состоит в преобразовании обыкновенных дифференциальных уравнений в алгебраические. Он основан на использовании одного из методов численного интегрирования.

Если задано дифференциальное уравнение

(3.1)

и начальные условия , то очередное значение может быть получено интегрированием (3.1):

(3.2)

Определенный интеграл в (3.2) численно равен площади под кривой на интервале (рис. 3.2).

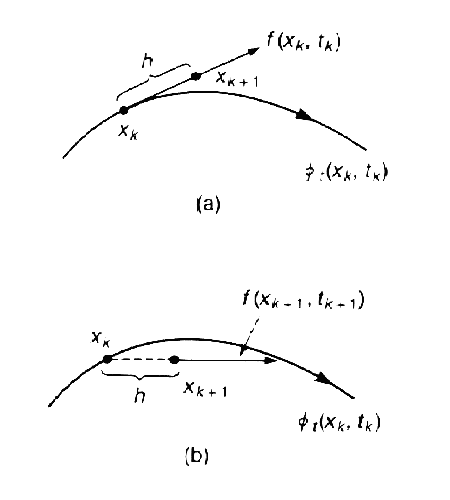
Приближенно эта площадь может быть вычислена как площадь прямоугольника, высота которого равна значению функции на левой границе интервала или значению на правой границе интервала. Очевидно, площади обоих прямоугольников, ограниченных сверху отрезками 1 и 2 на рис. 3.3, будут тем ближе к точному значению интеграла, чем меньше шаг интегрирования .

Подставив в (3.2) приближенные значения интеграла, можно получить две формулы:

(3.3)

. (3.4)

Выражение (3.3) представляет собой формулу явного метода Эйлера. Называется метод явным потому, что неизвестное значение 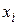может быть непосредственно вычислено по известному значению в предыдущей точке.

Формула (3.4) соответствует неявному методу Эйлера. Здесь в правой части выражения используется неизвестное значение 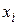, поэтому вычислить его непосредственно по этой формуле нельзя.

Более точное значение интеграла (3.2) дает метод трапеций, которому соответствует отрезок 3 на рис. 3.3. Тогда

. (3.5)

Эта формула относится, очевидно, тоже к неявным.

Для явных методов процедура формирования модели для численного интегрирования ограничивается алгебраизацией исходных дифференциальных уравнений. В частности, формула (3.3) не требует дальнейших преобразований и готова для применения.

Для неявных методов дальнейшие действия зависят от того, какой метод решения системы нелинейных уравнений реализован в данном пакете. Одним из вариантов может быть использование итерационного метода Ньютона, который, как известно, обладает наибольшей скоростью сходимости среди практически применяемых методов, и в котором многократно решается система линеаризованных алгебраических уравнений.

В этом случае реализуется второй этап подготовки математических моделей для неявных методов, который состоит в линеаризации нелинейных алгебраических уравнений, т.е. в разложении нелинейных функций в ряд Тэйлора и сохранении в результате только линейных членов.

Пусть задано нелинейное алгебраическое уравнение

(3.6)

где – вектор переменных.

Разложение (3.6) в ряд Тэйлора с сохранением только линейных членов дает приближенную замену

(3.7)

где –начальное приближение, в качестве которого берутся значения переменных на предыдущем шаге интегрирования;

– неизвестное значение переменной на шаге интегрирования.

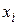
Выражение (3.7) может быть записано как линейное алгебраическое уравнение

,(3.8)

где – вычисляется для известных значений переменных на предыдущем шаге интегрирования;

Таким образом, процесс численного моделирования в общем случае нелинейных систем неявными методами состоит в формировании и решении на каждом шаге интегрирования системы линейных алгебраических уравнений

, (3.9)

которая включает компонентные и топологические уравнения моделируемой схемы. При этом, процедурам алгебраизации и линеаризации подвергаются только компонентные уравнения, так как топологические уравнения всегда линейные алгебраические.

Рассмотрим пример связанный с подготовкой модели для численного решения нелинейного дифференциального уравнения второго порядка

Первым шагом является сведение данного уравнения к задаче Коши, т.е. к системе уравнений первого порядка за счет введения новой переменной :

Явные формулы метода Эйлера имеют вид

Неявные формулы запишутся следующим образом:

Для перехода к матричной записи выполним ряд преобразований:

Здесь ,

Матричная запись имеет вид

.

Формулу (3.7), вообще говоря, необходимо применять итерационно. Решение этого уравнения, найденное для заданного начального приближения , следует использовать в качестве очередного приближения в (3.7) и повторять формирование и решение линейного алгебраического уравнения до тех пор, пока два последовательных приближения не станут близкими с заданной точностью. При численном моделировании можно ограничиться только одной итерацией, выбирая достаточно малый шаг интегрирования и учитывая, что при этом значения переменных на предыдущем шаге являются достаточно хорошим приближением.

3.2.3. Выбор между явными и неявными методами
в процедурах моделирования технических систем

Выбор между явными и неявными методами представляет серьезную проблему. Многие специалисты считают неявные методы более мощным и универсальным инструментом для решения задач моделирования технических систем [23, 15]. Следует, однако, заметить, что лишь недавно появились достаточно мощные и универсальные системы автоматизированного моделирования, такие, как, например, MATLAB или МВТУ [17], допускающие выбор явного или неявного метода решения задачи. Раньше использовались либо явные, либо неявные методы, так как это требовало разных компонентных моделей.

В современных перспективных системах автоматизированного моделирования, пригодных для моделирования технических систем, применяются, как правило, неявные методы численного интегрирования. Неявные методы лучше приспособлены для решения систем дифференциальных и алгебраических уравнений, к тому же они более устойчивы. В результате, несмотря на большие затраты машинного времени на каждом шаге интегрирования, связанные с необходимостью решения СЛАУ, общие затраты могут быть значительно меньше за счет увеличения шага интегрирования и уменьшения общего количества шагов.

Рассмотрим эту особенность неявных методов на примере явного и неявного методов Эйлера [21], определяемых формулами (3.3) и (3.4), соответственно.

Применим указанные формулы для численного интегрирования простейшего линейного дифференциального уравнения

.

Характеристическое уравнение данной динамической системы имеет вид

, или ,

где – постоянная времени системы.

Единственный полюс системы находится в левой полуплоскости, следовательно, исходная система устойчива. Соответственно, любое решение уравнения, при , стремится к нулю.

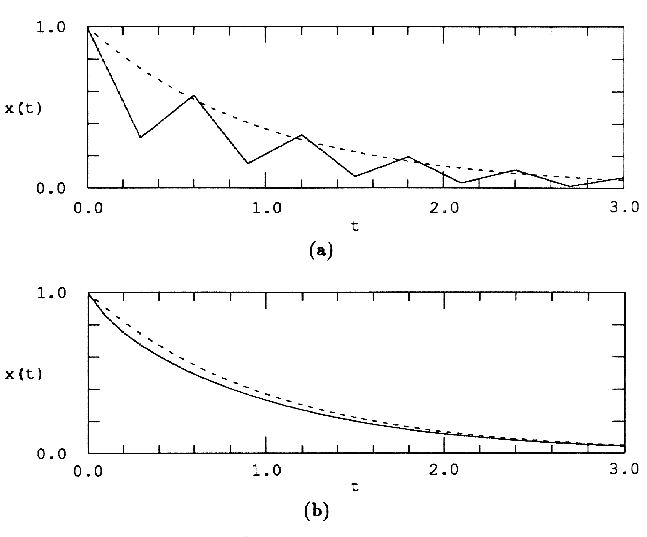
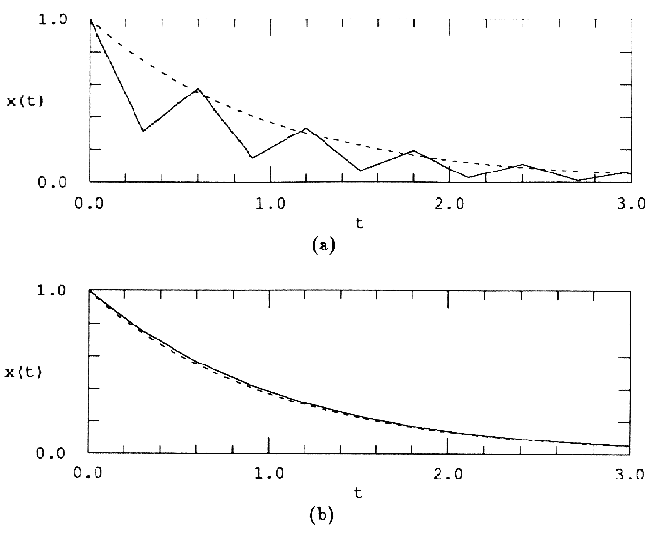
Разностное уравнение, соответствующее численному решению явным методом Эйлера, запишется как

.

Известно, что условием устойчивости полученного разностного уравнения является

или .

Это означает, что выбор может качественно изменить вид решения, превратив устойчивый процесс в неустойчивый.

Таким образом, на шаг интегрирования наложено очевидное ограничение – он не может быть больше постоянной времени системы, иначе дискретная аппроксимация станет неустойчивой. Если система имеет несколько постоянных времени, то подобное ограничение связывает шаг интегрирования с самой маленькой постоянной времени.

Переход к методам более высокого порядка мало меняет картину. Для метода Рунге – Кутты 4-го порядка требование устойчивости ограничивает шаг величиной , или, в более общем виде, , где – максимальное собственное значение матрицы Якоби [29].

Применение неявного метода Эйлера к той же системе дает

,

где ограничение на величину шага выглядит по-другому:

,

что позволяет выбрать шаг любой величины, ориентируясь только на требуемый уровень погрешности.

Видео:Метод ЭйлераСкачать

Интегрирование уравнений движения

Симуляция физики делает небольшие предсказания на основании законов физики. Эти предсказания на самом деле достаточно просты, что-то вроде «если объект вот здесь и он движется с такой скоростью в этом направлении, то за краткий промежуток времени он окажется вот тут». Мы создаём такие предсказания с помощью математической техники под названием интегрирование.

Темой этой статьи как раз и будет реализация такого интегрирования.

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений. Неявный метод Эйлера. Ложкин С.А.Скачать

Интегрирование уравнений движения

Вы можете помнить из курса старшей школы или вуза, что сила равна произведению массы на ускорение.

Преобразуем это уравнение и увидим, что ускорение равно силе, делённой на массу. Это соответствует нашим интуитивным ожиданиям, потому что тяжёлые объекты труднее бросать.

Ускорение — это темп изменения скорости от времени:

Аналогично, скорость — это темп изменения позиции от времени:

Это значит, что если мы знаем текущие позицию и скорость объекта, а также приложенные к нему силы, то сможем проинтегрировать, чтобы найти его позицию и скорость в определённый момент времени.

Видео:Решение системы дифференциальных уравнений методом ЭйлераСкачать

Численное интегрирование

Если вы не изучали дифференциальные уравнения в вузе, то можете вздохнуть спокойно — вы почти в такой же ситуации, что и те, кто их изучал, потому что мы не будем решать дифференциальные уравнения аналитически. Вместо этого мы будем искать решение численным интегрированием.

Вот как работает численное интегрирование: во-первых, начнём с исходной позиции и скорости, затем сделаем небольшой шаг вперёд, чтобы найти скорость и позицию в будущем. Затем повторим это, двигаясь вперёд небольшими шагами, используя результат предыдущих вычислений как исходную точку следующих.

Но как нам найти изменение скорости и позиции на каждом шаге?

Ответ лежит в уравнениях движения.

Давайте назовём наше текущее время t, а шаг времени dt или «delta time».

Теперь мы можем представить уравнения движения в понятном всем виде:

Интуитивно это понятно: если вы находитесь в автомобиле, движущемся со скоростью 60 км/ч, то за один час вы проедете 60 км. Аналогично, автомобиль, ускоряющийся на 10 км/ч в секунду, через 10 секунд будет двигаться на 100 км/ч быстрее.

Разумеется, эта логика сохраняется, только когда ускорение и скорость постоянны. Но даже если они меняются, то это для начала вполне неплохая аппроксимация.

Давайте представим это в коде. Начнём с стационарного объекта массой один килограмм и приложим к нему постоянную силу в 10 кН (килоньютонов) и сделаем шаг вперёд, принимая, что один временной шаг равен одной секунде:

Вот каким будет результат:

Как вы видите, на каждом шаге мы знаем и позицию, и скорость объекта. Это и есть численное интегрирование.

Видео:Численное решение задачи Коши методом ЭйлераСкачать

Явный метод Эйлера

Вид интегрирования, который мы только что использовали, называется явным методом Эйлера.

Он назван в честь швейцарского математика Леонарда Эйлера, впервые открывшего эту технику.

Интегрирование Эйлера — это простейшая техника численного интегрирования. Она точна на 100% только когда темп изменений в течение шага времени постоянен.

Поскольку в примере выше ускорение постоянно, интегрирование скорости выполняется без ошибок. Однако мы ещё интегрируем и скорость для получения позиции, а скорость увеличивается из-за ускорения. Это значит, что в проинтегрированной позиции возникает ошибка.

Но насколько велика эта ошибка? Давайте выясним!

Существует аналитическое решение движения объекта при постоянном ускорении. Мы можем использовать его, чтобы сравнить численно интегрированную позицию с точным результатом:

Через 10 секунд объект должен был переместиться на 500 метров, но явным метод Эйлера даёт нам результат 450. То есть погрешность в целых 50 метров всего за 10 секунд!

Кажется, что это невероятно плохо, но в играх обычно для шага физики берётся не такой большой временной интервал. На самом деле, физика обычно вычисляется с частотой, примерно равной частоте кадров дисплея.

Если задать шаг dt = 1 ⁄₁₀₀, то мы получим гораздо лучший результат:

Как вы видите, это достаточно хороший результат, определённо вполне достаточный для игры.

Видео:МЗЭ 2022 Численное решение дифференциальных уравнений Метод Эйлера Ложкин С. А.Скачать

Почему явный метод Эйлера не (всегда) так уж хорош

С достаточно малым шагом времени явный метод Эйлера при постоянном ускорении даёт вполне достойные результаты, но что будет, если ускорение не постоянно?

Хорошим примером переменного ускорения является система пружинного амортизатора.

В этой системе масса присоединена к пружине, и её движение гасится чем-то вроде трения. Существует сила, пропорциональная расстоянию до объекта, которая притягивает его к исходной точке, и сила, пропорциональная скорости объекта, но направленная в противоположном направлении, которая замедляет его.

Здесь ускорение в течение шага времени совершенно точно изменяется, но эта постоянно меняющаяся функция является сочетанием позиции и скорости, которые сами постоянно изменяются за шаг времени.

Вот пример гармонического осциллятора с затуханием. Это хорошо изученная задача, и для него существует аналитическое решение, которое можно использовать для проверки результата численного интегрирования.

Давайте начнём со слабозатухающей системы, в которой масса колеблется рядом с исходной точкой, постепенно замедляясь.

Вот входные параметры системы масса-пружина:

• Масса: 1 килограмм
• Исходная позиция: 1000 метров от исходной точки
• Коэффициент упругости по закону Гука: k = 15
• Коэффициент затухания по закону Гука: b = 0.1

И вот график точного решения:

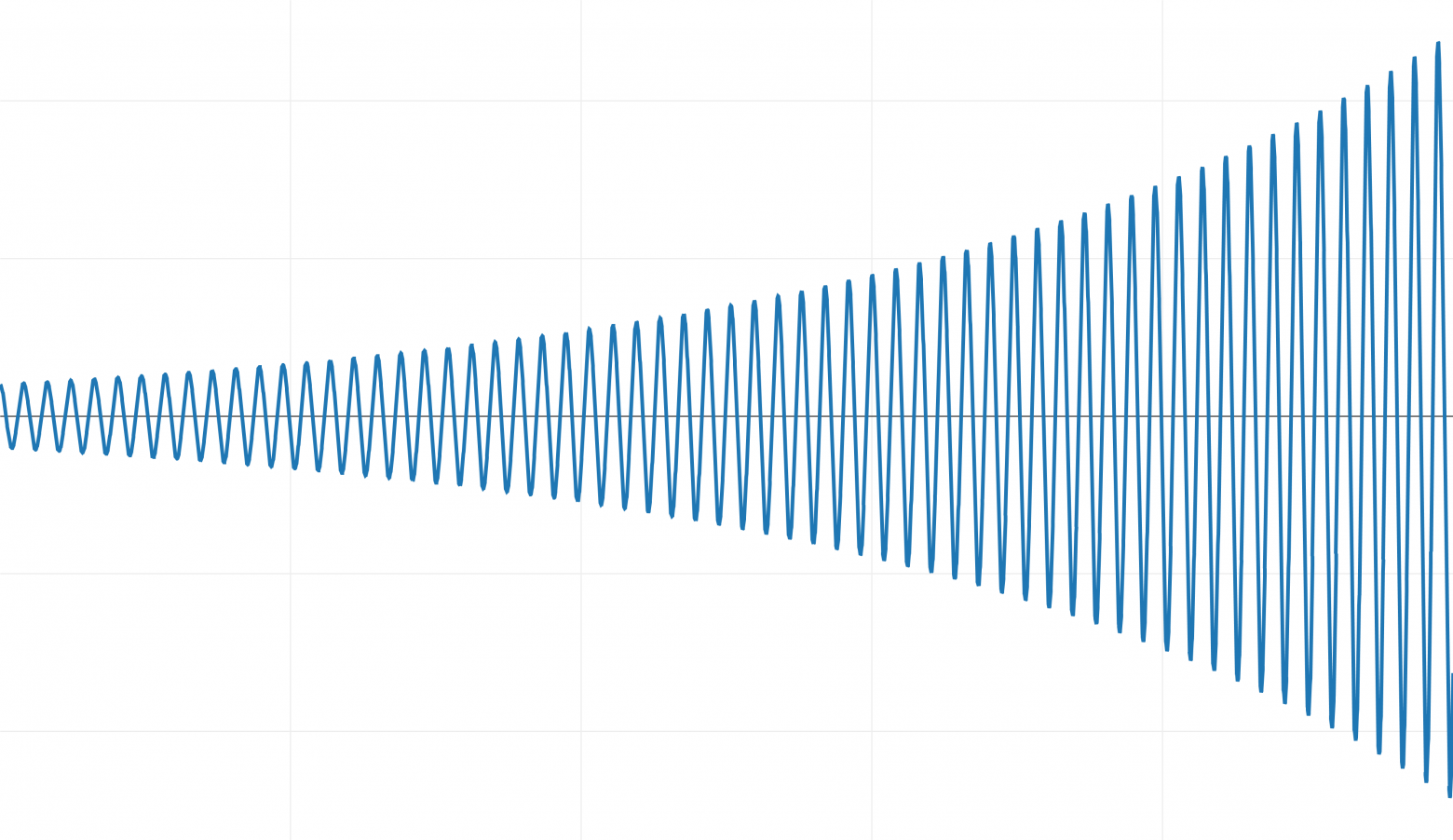
Если для интегрирования этой системы мы применим явный метод Эйлера, то получим следующий результа, который я отмасштабировал по вертикали:

Вместо затухания и сближения с исходной точкой, система со временем набирает энергию!

При интегрировании явным методом Эйлера и с dt= 1 ⁄₁₀₀ такая система нестабильна.

К сожалению, поскольку мы уже интегрируем с малым шагом времени, то не имеем практичных способов повышения точности. Даже если мы уменьшим шаг времени, то всегда будет коэффициент упругости k, при котором мы получим такое поведение.

Видео:03 Одношаговые явные методы численного интегрированияСкачать

Симплектический метод Эйлера

Мы можем рассмотреть ещё один интегратор — симплектический метод Эйлера.

В большинстве коммерческих игровых физических движков используется этот интегратор.

Переход от явного к симплектическому методу Эйлера заключается только в замене:

Использование симплектического интегратора Эйлера при dt = 1 ⁄₁₀₀ для системы пружинного амортизатора даёт стабильный результат, очень близкий к точному решению:

Даже несмотря на то, что симплектический метод Эйлера имеет ту же степень точности, что и явный метод (степень 1), при интегрировании уравнений движения мы получаем намного лучший результат, потому что оно является симплектическим.

Видео:Численное решение системы дифференциальных уравнений(задачи Коши)Скачать

Существует множество других методов интегрирования

И теперь нечто совершенно другое.

Неявный метод Эйлера — это способ интегрирования, хорошо подходящий для интегрирования жёстких уравнений, которые при других методах становятся нестабильными. Его недостаток заключается в том, что он требует решения системы уравнений на каждом шаге времени.

Интегрирование Верле обеспечивает бо́льшую точность, чем неявный метод Эйлера, и требует меньше памяти при симуляции большого числа частиц. Это интегратор второй степени, который тоже является симплектическим.

Существует целое семейство интеграторов, называемое методами Рунге-Кутты. На самом деле, явный метод Эйлера считается частью этого семейства, но в него входят интеграторы и более высокого порядка, самым классическим из которых является метод Рунге-Кутты порядка 4 (Runge Kutta order 4) или просто RK4.

Это семейство интеграторов названо в честь открывших их немецких физиков: Карла Рунге и Мартина Кутты.

RK4 — это интегратор четвёртого порядка, то есть накапливаемая ошибка имеет порядок четвёртой производной. Это делает метод очень точным, гораздо более точным, чем явный и неявный методы Эйлера, имеющие только первый порядок.

Но хотя он более точен, нельзя сказать, что RK4 автоматически становится «лучшим» интегратором, или даже что он лучше симплектического метода Эйлера. Всё гораздо сложнее. Тем не менее, это довольно интересный интегратор и его стоит изучить.

Видео:Численное интегрирование методом ЭйлераСкачать

Реализация RK4

Существует уже много объяснений математики, используемой в RK4. Например: здесь, здесь и здесь. Я настоятельно рекомендую изучить его выведение и понять, как и почему он работает на математическом уровне. Но я понимаю, что целевая аудитория этой статьи — программисты, а не математики, поэтому мы здесь будем рассматривать только реализацию. Так что давайте приступим.

Прежде чем приступить, давайте зададим состояние объекта как struct в C++, чтобы можно было удобно хранить позицию и скорость в одном месте:

Также нам нужна структура для хранения производных значений состояний:

Теперь нам нужна функция для вычисления состояния физики из t в t+dt с помощью одного набора производных, а после этого для вычисления производных в новом состоянии:

Функция ускорения управляет всей симуляцией. Давайте используем её в системе пружинного амортизатора и вернём ускорение для единичной массы:

То, что нужно здесь записать, разумеется, зависит от симуляции, но необходимо структурировать симуляцию таким образом, чтобы можно было вычислять ускорение внутри этого метода для заданных состояния и времени, в противном случае он не подойдёт для интегратора RK4.

Наконец, мы получаем саму процедуру интегрирования:

Интегратор RK4 делает выборку производной в четырёх точках, чтобы определить кривизну. Заметьте, как производная a используется при вычислении b, b используется при вычислении c, и c для d. Эта передача текущей производной в вычисление следующей и даёт интегратору RK4 его точность.

Важно то, что каждая из этих производных a, b, c и d будет разной, когда темп изменения в этих величинах является функцией времени или функцией самого состояния. Например, в нашей системе пружинного амортизатора ускорение является функцией текущей позиции и скорости, которые меняются в шаге времени.

После вычисления четырёх производных наилучшая общая производная вычисляется как взвешенная сумма, полученная из разложения в ряд Тейлора. Эта комбинированная производная используется для перемещения позиции и скорости вперёд во времени, точно так же, как мы делали это в явном интеграторе Эйлера.

Видео:01.02. Модель SIR. Численное решение системы дифференциальных уравнений с помощью SciPyСкачать

Сравнение симплектического метода Эйлера и RK4

Давайте подвергнем проверке интегратор RK4.

Очевидно, что поскольку он является интегратором более высокого порядка (четвёртый против первого) он наглядно будет более точен, чем симплектический метод Эйлера, правда?

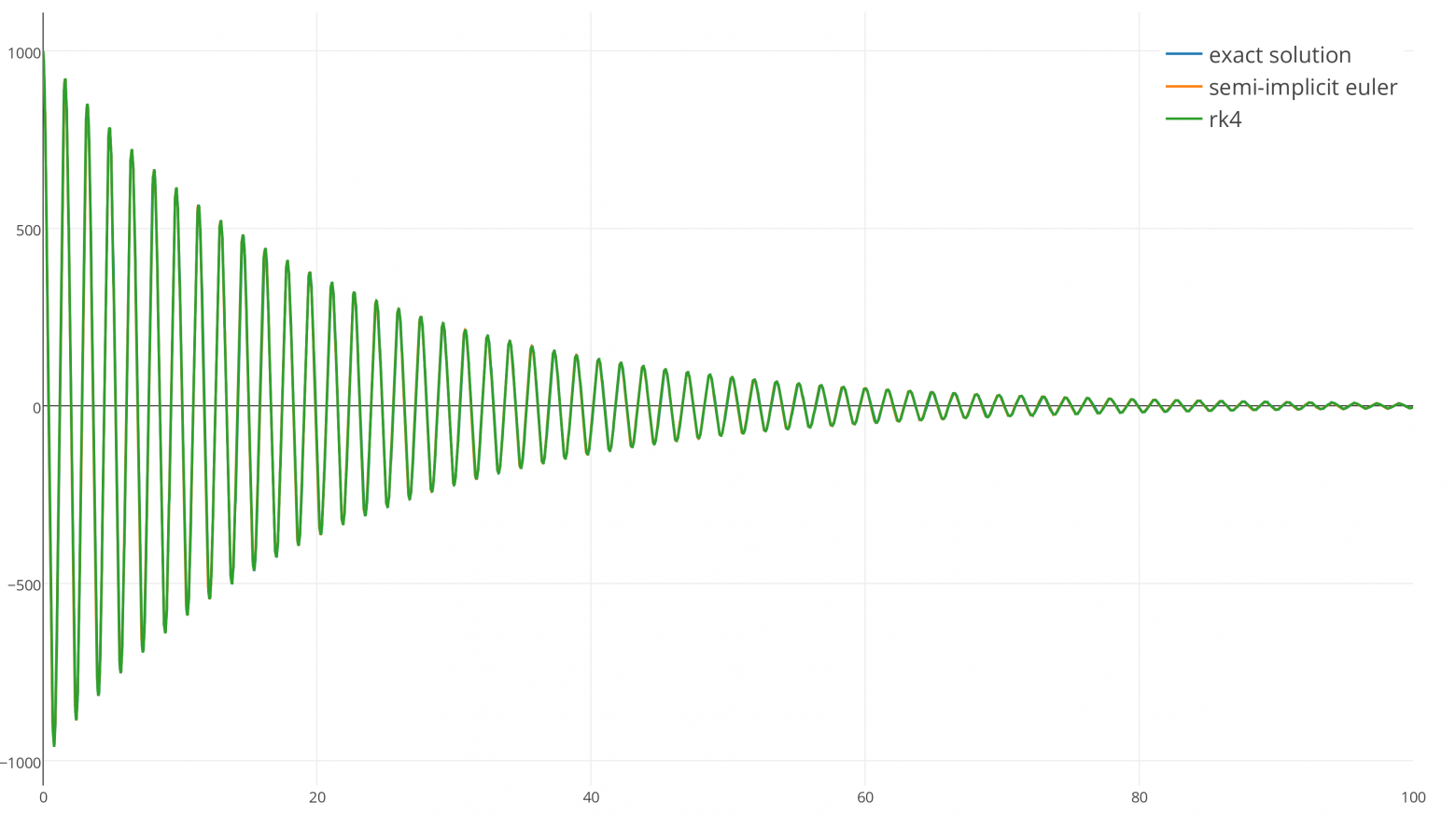
Неправда. Оба интегратора так близки к точному результату, что при таком масштабе почти невозможно найти между ними разницу. Оба интегратора стабильны и очень хорошо повторяют точное решение при dt= 1 ⁄₁₀₀.

При увеличении видно, что RK4 действительно более точен, чем симплектический метод Эйлера, но стоит ли эта точность сложности и лишнего времени выполнения RK4? Трудно судить.

Давайте постараемся и посмотрим, сможем ли мы найти значительное различие между двумя интеграторами. К сожалению, мы не сможем долго наблюдать за этой системой, потому что она быстро затухает до нуля, поэтому давайте перейдём к простому гармоническому осциллятору, который колеблется бесконечно и без затуханий.

Вот точный результат, к которому мы будем стремиться:

Чтобы усложнить интеграторам задачу, давайте увеличим шаг времени до 0,1 секунды.

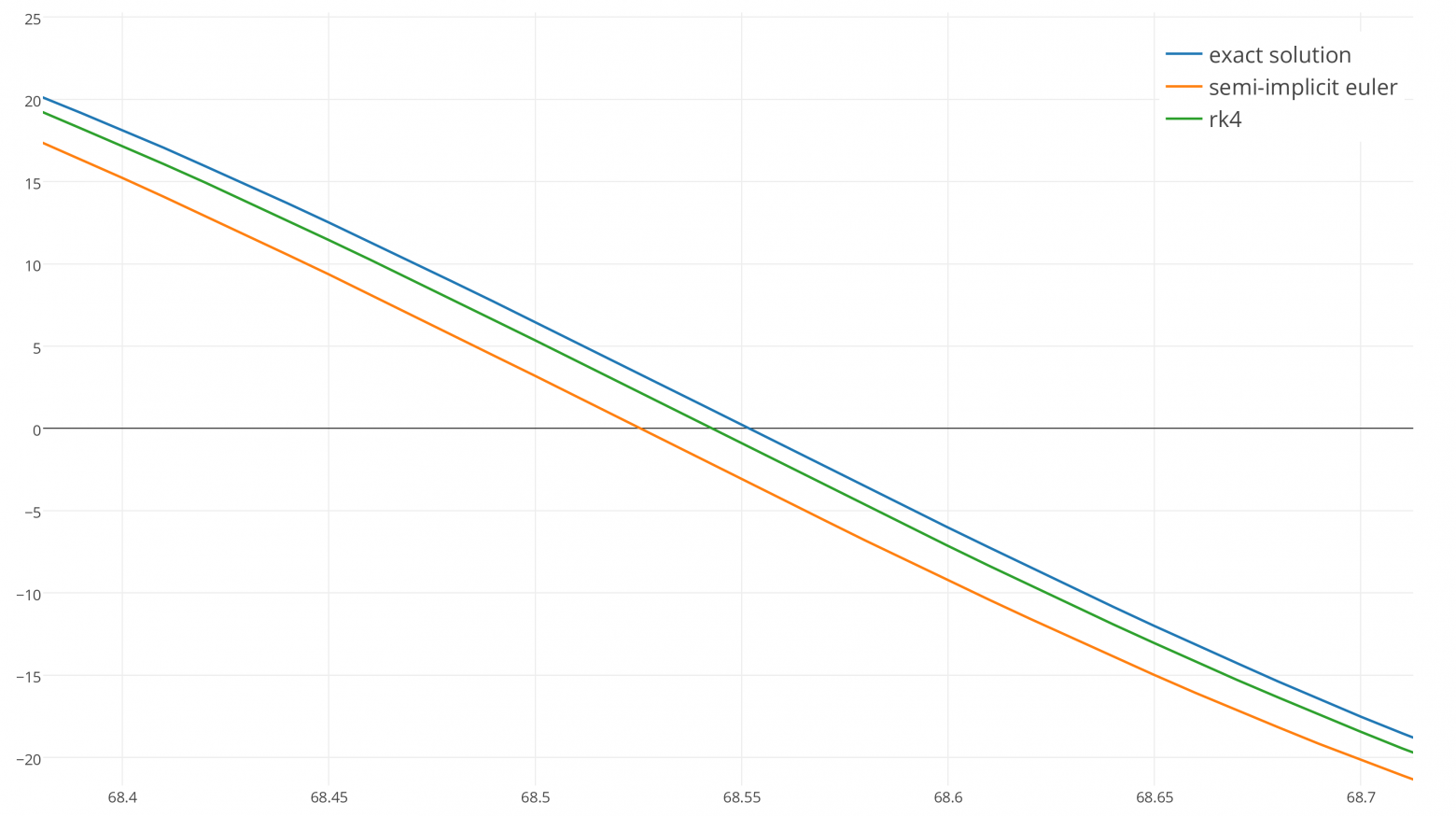
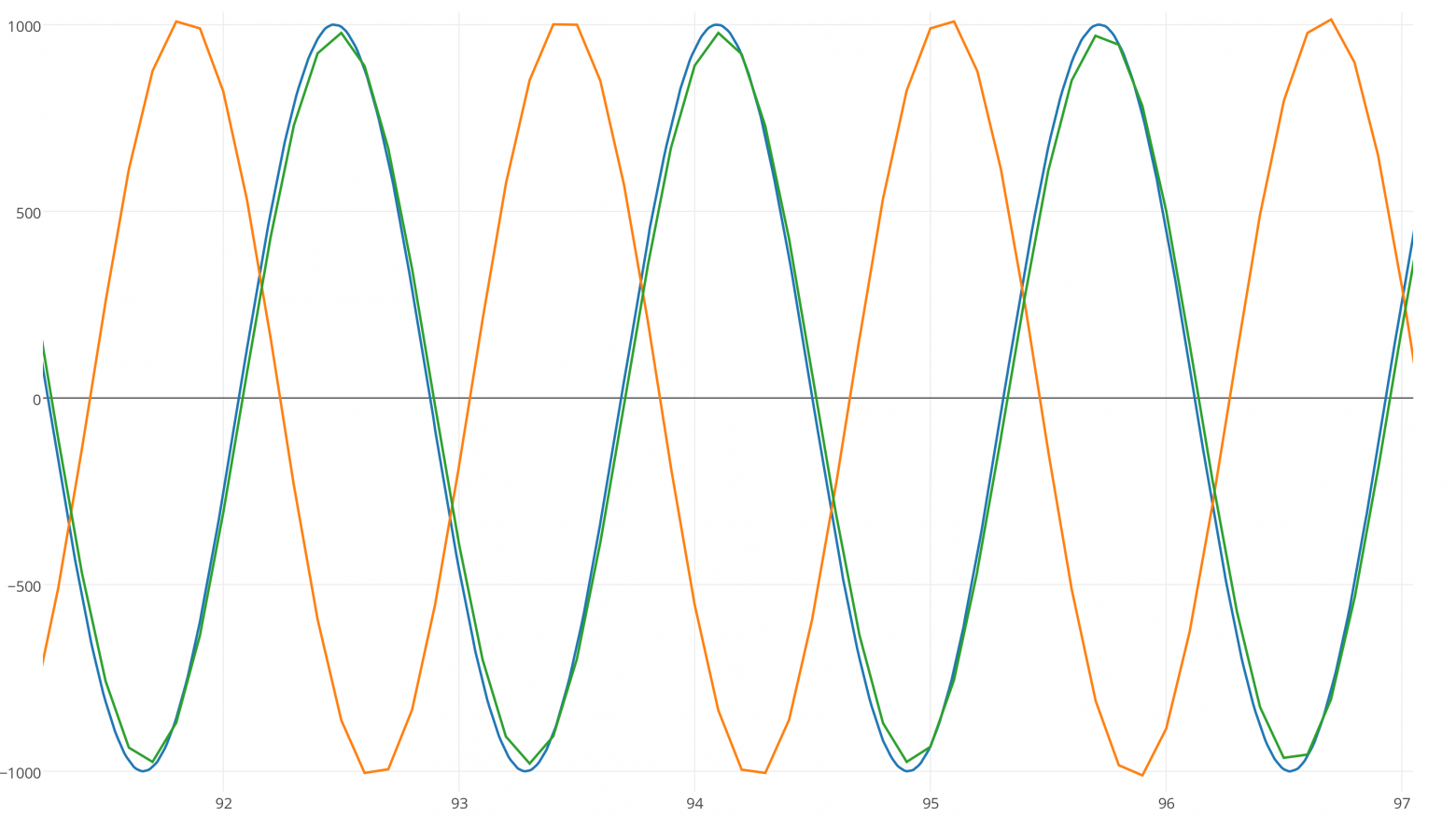
Теперь запустим интеграторы на 90 секунд и увеличим масштаб:

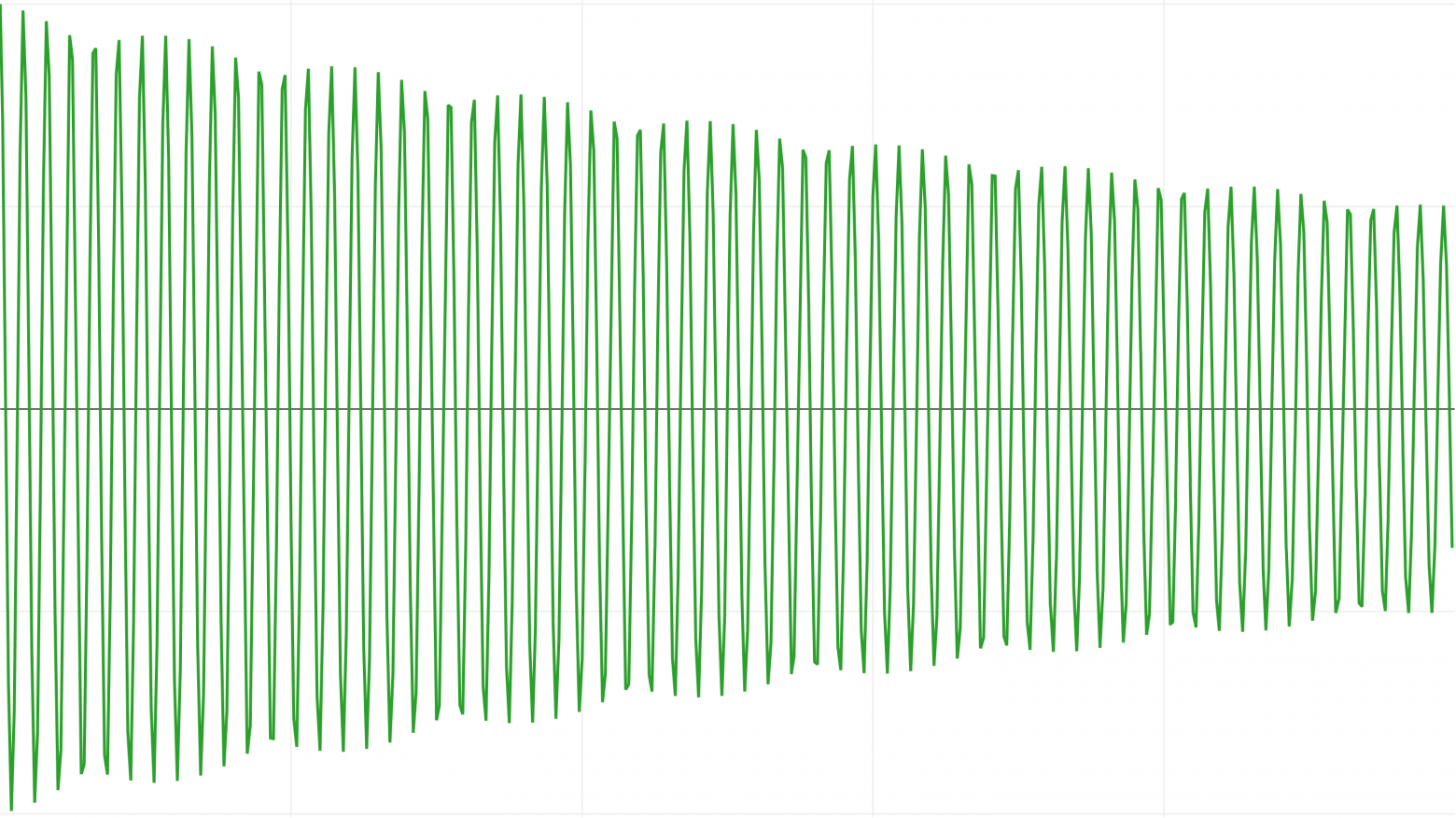
Через 90 секунд симплектический метод Эйлера (оранжевая кривая) сдвинулся по фазе относительно точного решения, потому что его частота немного отличалась, в то время как зелёная кривая RK4 соответствует частоте, но теряет энергию!

Мы чётко можем это заметить, увеличив шаг времени до 0,25 секунды.

RK4 сохраняет верную частоту, но теряет энергию:

А симплектический метод Эйлера в среднем намного лучше сохраняет энергию:

Но от сдвигается от фазы. Какой интересный результат! Как вы видите, если RK4 имеет более высокий порядок точности, то он не обязательно «лучше». В этом вопросе есть множество нюансов.

Видео:Линейное дифференциальное уравнение Коши-ЭйлераСкачать

Заключение

Мы реализовали три различных интегратора и сравнили результаты.

1. Явный метод Эйлера
2. Симплектический метод Эйлера
3. Метод Рунге-Кутты порядка 4 (RK4)

Так какой же интегратор стоит использовать в игре?

Я рекомендую симплектический метод Эйлера. Он «дёшев» и прост в реализации, гораздо стабильнее явного метода Эйлера и в среднем стремится к сохранению энергии даже при близких к предельным условиях.

Если вам действительно нужна бОльшая точность, чем у симплектического метода Эйлера, я рекомендую посмотреть на симплектические интеграторы более высокого порядка, рассчитанные на гамильтоновы системы. Таким образом вы изучите более современные техники интегрирования высокого порядка, которые лучше подходят для симуляций, чем RK4.

И наконец, если вы всё ещё пишете в игре такое:

То потратьте секунду и замените эти строки на:

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Численное интегрирование системы дифференциальных уравнений явный и неявный методы эйлера

последовательностью точек x₀,x₁. в соответствующие моменты времени t₀,t₁. Значения точек должны удоволетворять приближенному равенству

Если специально не оговорено иное, то предполагается, что моменты времени выбираются через равные интервалы с величиной шага h>0, то есть

Аппроксимируем производную в момент времени t_k соотношением

При такой аппроксимации уравнение (1) примет вид:

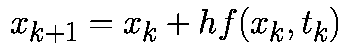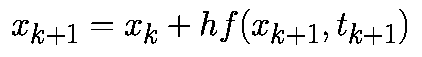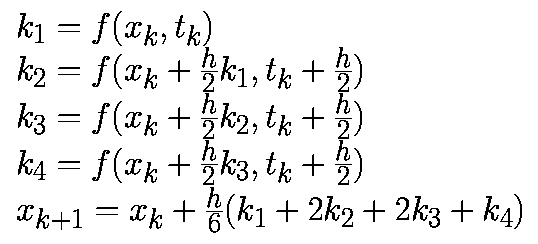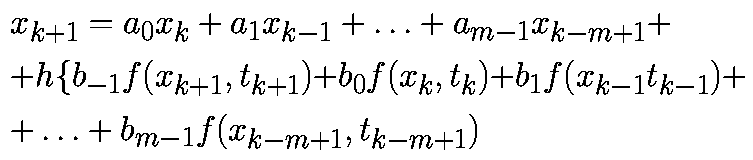Формула (2) известна как прямой метод Эйлера.

На рис.1(a) показана графическая интерпретация прямого метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(x_k,t_k).

Рис.1 Иллюстрация алгоритмов (а) прямого метода Эйлера, (b) обратного метода Эйлера

Меньшее значение величины шага h в итоге дает точки аппроксимации чаще и, как демонстрирует рис.2, приводит к большей точности интегрирования, что приобретает математический смысл, поскольку (2) стремится к (1) при h->0.

Рис.2 Влияние величины шага. Уравнение dx/dt=-6x+5t -t интегрируется от x=1 прямым методом Эйлера при h=0.3 (а) и при h=0.1 (b). Точное решение показано штриховой линией.

Обратный метод Эйлера подобен прямому, но есть одно отличие в аппроксимации для производной

Такая аппроксимация дает формулу обратного метода Эйлера:

На рис.1(b) показана геометрическая интерпретация обратного метода Эйлера. На (k+1)-ом шаге векторное поле предполагается (локально) постоянным со значением f(x_k+1,t_k+1).

Обратный метод Эйлера — это пример неявного алгоритма интегрирования , где x_k+1 является функцией от самой себя. И напротив, прямой метод Эйлера представляет собой явный алгоритм. В неявных алгоритмах для определения x_k+1 требуются дополнительные вычисления, но они по сравнению с аналогичными прямыми алгоритмами более устойчивы и дают более высокую точность вычислений (см. рис.3). Возможно это обусловлено наличием члена x_k+1 в правой части формулы, что может рассматриваться как вид обратной связи.

Рис.3 Та же система, что и на рис.2 проинтегрирована от x₀=1.0 с h=0.3 (a) прямым методом Эйлера, (b) обратным методом Эйлера. Точное решение показано штриховой линией.

Трапецеидальный алгоритм имеет вид:

Имеется целое семейство уравнений Рунге-Кутта второго порядка. Мы рассмотрим модифицированный алгоритм Эйлера-Коши, заданный соотношением:

Из этой формулы следует, что модифицированный алгоритм Эйлера-Коши включает два этапа. На первом этапе с помощью прямого метода Эйлера происходит перемещение на пол шага вперед к моменту времени (t_k+h/2):

На втором этапе это промежуточное значение используется для аппроксимации векторного поля с помощью итераций Эйлера прямого типа:

Как и в случае алгоритма второго порядка метод Рунге-Кутта четвертого порядка относится к явным алгоритмам. Он использует промежуточные моменты времени для для вычисления состояния в момент времени t_k+1. Следующие формулы определяют алгоритм Рунге-Кутта четвертого порядка:

Для определенных выше алгоритмов на каждом шаге требуется только одна начальная точка x_k. Такие алгоритмы называются одношаговыми. Одношаговые алгоритмы высокого порядка имеют высокую точность, но они не эффективны, если велики затраты на вычисление f. Например, алгоритм Рунге-Кутта четвертого порядка требует на шаге четыре значения f. Кроме того, на текущем шаге не выполняются оценки функций с целью их использования на последующих шагах.
В отличие от одношаговых алгоритмов, многошаговые алгоритмы повторно используют предыдущую информацию о траектории. В m-шаговом алгоритме для определения x_k+1 используют m предыдущих точек x_k, x_k-1. x_k-m+1 и значения f в этих точках. Общая формула m-шагового алгоритма имеет вид

Локальная ошибка определяется как ошибка на шаге алгоритма:

Для m-шаговых алгоритмов предполагается, что предыдущие m точек x_k-i при i=0. m-1 являются точно заданными, т.е.

Ошибка усечения — это локальная ошибка, которая получилась бы в результате выполнения алгоритма на компьютере с бесконечной точностью.
Другими словами, подразумевается, что эта локальная ошибка возникает помимо ошибки округления. Также важно помнить, что для m-шаговых алгоритмов предыдущие m точек x_k. x_k-m+1 предполагаются точно заданными.
Ошибка усечения берет свое название от алгоритмов, основанных на рядах Тейлора (например, Рунге-Кутта). Эти алгоритмы были бы точными, если бы использовались полные (бесконечные) ряды. Ошибка возникает при усечении ряда до конечного числа членов.
Ошибка усечения зависит только от алгоритма. Она не зависит от используемого компьютера и, следовательно, может быть проанализирована. Для алгоритмов Рунге-Кутта K-го порядка, при подходящих условиях, локальная ошибка усечения представляет собой

где «альфа» зависит от K, f и x_k, но не зависит от h. Для многошагового алгоритма K-го порядка локальная ошибка усечения имеет вид

Глобальнае ошибка округления — это простое накопление локальных ошибок округления. Если локальная ошибка составляет «эпсилон», то ошибка округления на единичном интервале будет

Подобно ошибке округления, локальная ошибка усечения также накапливается с каждым шагом. Для одношаговых алгоритмов K-го порядка локальная ошибка усечения составляет

Если пренебречь зависимостью a_k от x_k, то на единичном интервале времени ошибка усечения будет:

📽️ Видео

Метод Эйлера. Решение систем ДУСкачать

Дифференциальное уравнение. Формула ЭйлераСкачать

5 Численное решение дифференциальных уравнений Part 1Скачать

Пример решения задачи Коши методом Эйлера. Метод Эйлера с пересчетом.Скачать

Видеоурок "Системы диф. уравнений. Метод Эйлера"Скачать

Дифференциальные уравнения. Задача Коши. Метод Эйлера.Скачать

Лекция "Численное интегрирование дифференциальных уравнений" часть 1Скачать