ъБДБЮБ б. «тЕЫЕОЙЕ ХТБЧОЕОЙС»
оБРЙЫЙФЕ РТПЗТБННХ, ТЕЫБАЭХА ХТБЧОЕОЙЕ Ax 2 +Bx+C=0.
чЧПДСФУС ФТЙ ЮЙУМБ A, B, C. лБЦДПЕ ЙЪ ЬФЙИ ЮЙУЕМ — ГЕМПЕ Й РП НПДХМА ОЕ РТЕЧПУИПДЙФ 1000.
чЩЧЕДЙФЕ УОБЮБМБ ЛПМЙЮЕУФЧП ЛПТОЕК ЬФПЗП ХТБЧОЕОЙС, Б ЪБФЕН УБНЙ ЬФЙ ЛПТОЙ Ч РПТСДЛЕ ЧПЪТБУФБОЙС, ОЕ НЕОШЫЕ ЮЕН У ФТЕНС ЪОБЛБНЙ РПУМЕ ФПЮЛЙ.
еУМЙ ЛПТОЕК ВПМШЫЕ 1000, ЧЩЧЕДЙФЕ ПДОП ЮЙУМП −1 (НЙОХУ ПДЙО). еУМЙ ЛПТОЕК ОЕФ, ЧЩЧЕДЙФЕ 0 (ОПМШ).
ъБДБЮБ B. «рПМПЦЕОЙЕ ФПЮЕЛ ЧОЕ РТСНПК»
чЧПДСФУС УЕНШ ЮЙУЕМ — ЛППТДЙОБФЩ ДЧХИ ФПЮЕЛ ЧОЕ РТСНПК Й ЛПЬЖЖЙГЙЕОФЩ A, B Й C ЕЈ ХТБЧОЕОЙС.
чЩЧЕДЙФЕ ПДОХ УФТПЛХ «YES», ЕУМЙ ФПЮЛЙ МЕЦБФ РП ПДОХ УФПТПОХ РТСНПК, Й «NO» Ч РТПФЙЧОПН УМХЮБЕ.
ъБДБЮБ C. «рЕТЕУЕЮЕОЙЕ РТСНЩИ»
оБ РМПУЛПУФЙ ДБОЩ ДЧЕ РТСНЩЕ. лБЦДБС РТСНБС ЪБДБЕФУС РБТПК ФПЮЕЛ, ЮЕТЕЪ ЛПФПТЩЕ ПОБ РТПИПДЙФ. фТЕВХЕФУС ХУФБОПЧЙФШ, РЕТЕУЕЛБАФУС МЙ ЬФЙ РТСНЩЕ Й ОБКФЙ ЛППТДЙОБФЩ ФПЮЛЙ РЕТЕУЕЮЕОЙС.
чЧПДСФУС УОБЮБМБ ЛППТДЙОБФЩ ДЧХИ ТБЪМЙЮОЩИ ФПЮЕЛ, ЮЕТЕЪ ЛПФПТЩЕ РТПИПДЙФ РЕТЧБС РТСНБС, Б ЪБФЕН — ЛППТДЙОБФЩ ЕЭЕ ДЧХИ ТБЪМЙЮОЩИ (ОП, ВЩФШ НПЦЕФ, УПЧРБДБАЭЙИ У РЕТЧЩНЙ ДЧХНС) ФПЮЕЛ, ЮЕТЕЪ ЛПФПТЩЕ РТПИПДЙФ ЧФПТБС РТСНБС. лППТДЙОБФЩ ЛБЦДПК ФПЮЛЙ — ГЕМЩЕ ЮЙУМБ, РП НПДХМА ОЕ РТЕЧЩЫБАЭЙЕ 1000.
еУМЙ РТСНЩЕ ОЕ РЕТЕУЕЛБАФУС, ЧЩЧЕДЙФЕ ПДОП ЮЙУМП 0.
еУМЙ РТСНЩЕ УПЧРБДБАФ, ЧЩЧЕДЙФЕ 2.
еУМЙ РТСНЩЕ РЕТЕУЕЛБАФУС ТПЧОП Ч ПДОПК ФПЮЛЕ, ФП ЧЩЧЕДЙФЕ УОБЮБМБ ЮЙУМП 1, Б ЪБФЕН ДЧБ ЧЕЭЕУФЧЕООЩИ ЮЙУМБ — ЛППТДЙОБФЩ ФПЮЛЙ РЕТЕУЕЮЕОЙС.
19 БРТЕМС 2013. зЕПНЕФТЙС
ъБДБЮБ D. «рЕТРЕОДЙЛХМСТОБС РТСНБС»
рСФШ ЮЙУЕМ — ЛПЬЖЖЙГЙЕОФЩ A, B Й C ХТБЧОЕОЙС РТСНПК Й ЛППТДЙОБФЩ ОЕЛПФПТПК ФПЮЛЙ X, Y (ФПЮЛБ НПЦЕФ ВЩФШ ЛБЛ ОБ РТСНПК, ФБЛ Й ЧОЕ ЕЈ). чУЕ ЮЙУМБ ГЕМЩЕ, РП НПДХМА ОЕ РТЕЧПУИПДСФ 1000.
чЩЧЕДЙФЕ ФТЙ ЮЙУМБ — ЛПЬЖЖЙГЙЕОФЩ A, B Й C ХТБЧОЕОЙС РТСНПК, РЕТРЕОДЙЛХМСТОПК ЪБДБООПК Й РТПИПДСЭЕК ЮЕТЕЪ ЪБДБООХА ФПЮЛХ (У ФПЮОПУФША ОЕ НЕОЕЕ 5 ЪОБЛПЧ РПУМЕ ФПЮЛЙ).
ъБДБЮБ E. «рБТБММЕМШОБС РТСНБС»
дБОЩ ЮЕФЩТЕ ЮЙУМБ — ЛПЬЖЖЙГЙЕОФЩ A, B Й C ХТБЧОЕОЙС РТСНПК Й ЧЕМЙЮЙОБ R. чУЕ ЮЙУМБ ГЕМЩЕ, РП НПДХМА ОЕ РТЕЧПУИПДСФ 1000.
чЩЧЕДЙФЕ ФТЙ ЮЙУМБ — ЛПЬЖЖЙГЙЕОФЩ A, B Й C ХТБЧОЕОЙС МАВПК ЙЪ РТСНЩИ, РБТБММЕМШОЩИ ЪБДБООПК Й МЕЦБЭЙИ ПФ ОЕЈ ОБ ТБУУФПСОЙЙ R.
ъБДБЮБ F. «тБУУФПСОЙЕ ПФ ФПЮЛЙ ДП РТСНПК»
дБОЩ 5 ЮЙУЕМ — ЛППТДЙОБФЩ ФПЮЛЙ Й ЛПЬЖЖЙГЙЕОФЩ A, B Й C ХТБЧОЕОЙС РТСНПК. чУЕ ЮЙУМБ ГЕМЩЕ, ОЕ РТЕЧЩЫБАЭЙЕ РП НПДХМА 1000.
чЩЧЕДЙФЕ пдоп ЮЙУМП — ТБУУФПСОЙЕ ПФ ФПЮЛЙ ДП РТСНПК (У ФПЮОПУФША ОЕ НЕОЕЕ 5 ЪОБЛПЧ РПУМЕ ФПЮЛЙ).
ъБДБЮБ G. «тБУУФПСОЙЕ ПФ ФПЮЛЙ ДП ПФТЕЪЛБ»
дБОП 6 ЮЙУЕМ — ЛППТДЙОБФЩ ФПЮЛЙ Й ЛППТДЙОБФЩ ЛПОГПЧ ПФТЕЪЛБ. чУЕ ЮЙУМБ ГЕМЩЕ, ОЕ РТЕЧЩЫБАЭЙЕ РП НПДХМА 1000.
чЩЧЕДЙФЕ ПДОП ЮЙУМП — ТБУУФПСОЙЕ ПФ ФПЮЛЙ ДП ПФТЕЪЛБ (У ФПЮОПУФША ОЕ НЕОЕЕ 5 ЪОБЛПЧ РПУМЕ ФПЮЛЙ).
ъБДБЮБ H. «фПЮЛБ РЕТЕУЕЮЕОЙС ЧЩУПФ»
дБОЩ ЛППТДЙОБФЩ ФТЕИ ФПЮЕЛ, ОЕ МЕЦБЭЙИ ОБ ПДОПК РТСНПК X1, Y1, X2, Y2, X3, Y3. чУЕ ЮЙУМБ ГЕМЩЕ, РП НПДХМА ОЕ РТЕЧПУИПДСФ 1000.
чЩЧЕДЙФЕ ДЧБ ЮЙУМБ X, Y, ЪБДБАЭЙЕ ЛППТДЙОБФЩ ФПЮЛЙ РЕТЕУЕЮЕОЙС ЧЩУПФ Ч ФТЕХЗПМШОЙЛЕ, ПВТБЪПЧБООПН ЙУИПДОЩНЙ ФПЮЛБНЙ (У ФПЮОПУФША ОЕ НЕОЕЕ 5 ЪОБЛПЧ РПУМЕ ДЕУСФЙЮОПК ФПЮЛЙ).
ъБДБЮБ I. «фПЮЛБ РЕТЕУЕЮЕОЙС НЕДЙБО»
дБОЩ ЛППТДЙОБФЩ ФТЕИ ФПЮЕЛ, ОЕ МЕЦБЭЙИ ОБ ПДОПК РТСНПК X1, Y1, X2, Y2, X3, Y3. чУЕ ЮЙУМБ ГЕМЩЕ, РП НПДХМА ОЕ РТЕЧПУИПДСФ 1000.
чЩЧЕДЙФЕ ДЧБ ЮЙУМБ X, Y, ЪБДБАЭЙЕ ЛППТДЙОБФЩ ФПЮЛЙ РЕТЕУЕЮЕОЙС НЕДЙБО Ч ФТЕХЗПМШОЙЛЕ, ПВТБЪПЧБООПН ЙУИПДОЩНЙ ФПЮЛБНЙ (У ФПЮОПУФША ОЕ НЕОЕЕ 5 ЪОБЛПЧ РПУМЕ ДЕУСФЙЮОПК ФПЮЛЙ).
ъБДБЮБ J. «фПЮЛБ РЕТЕУЕЮЕОЙС ВЙУУЕЛФТЙУУ»
дБОЩ ЛППТДЙОБФЩ ФТЕИ ФПЮЕЛ, ОЕ МЕЦБЭЙИ ОБ ПДОПК РТСНПК X1, Y1, X2, Y2, X3, Y3. чУЕ ЮЙУМБ ГЕМЩЕ, РП НПДХМА ОЕ РТЕЧПУИПДСФ 1000.
чЩЧЕДЙФЕ ДЧБ ЮЙУМБ X, Y, ЪБДБАЭЙЕ ЛППТДЙОБФЩ ФПЮЛЙ РЕТЕУЕЮЕОЙС ВЙУУЕЛФТЙУУ Ч ФТЕХЗПМШОЙЛЕ, ПВТБЪПЧБООПН ЙУИПДОЩНЙ ФПЮЛБНЙ (У ФПЮОПУФША ОЕ НЕОЕЕ 5 ЪОБЛПЧ РПУМЕ ДЕУСФЙЮОПК ФПЮЛЙ).
ъБДБЮБ K. «чРЙУБООБС ПЛТХЦОПУФШ»
дБОЩ ЛППТДЙОБФЩ ФТЕИ ФПЮЕЛ, ОЕ МЕЦБЭЙИ ОБ ПДОПК РТСНПК X1, Y1, X2, Y2, X3, Y3. чУЕ ЮЙУМБ ГЕМЩЕ, РП НПДХМА ОЕ РТЕЧПУИПДСФ 1000.
чЩЧЕДЙФЕ ФТЙ ЮЙУМБ X, Y, R, ЪБДБАЭЙЕ ЛППТДЙОБФЩ ГЕОФТБ Й ТБДЙХУ ПЛТХЦОПУФЙ, ЧРЙУБООПК Ч ФТЕХЗПМШОЙЛ, ПВТБЪПЧБООЩК ДБООЩНЙ ФПЮЛБНЙ (У ФПЮОПУФША ОЕ НЕОЕЕ 5 ЪОБЛПЧ РПУМЕ ДЕУСФЙЮОПК ФПЮЛЙ).
ъБДБЮБ L. «пРЙУБООБС ПЛТХЦОПУФШ»
дБОЩ ЛППТДЙОБФЩ ФТЕИ ФПЮЕЛ, ОЕ МЕЦБЭЙИ ОБ ПДОПК РТСНПК X1, Y1, X2, Y2, X3, Y3. чУЕ ЮЙУМБ ГЕМЩЕ, РП НПДХМА ОЕ РТЕЧПУИПДСФ 1000.
чЩЧЕДЙФЕ ФТЙ ЮЙУМБ X, Y, R, ЪБДБАЭЙЕ ЛППТДЙОБФЩ ГЕОФТБ Й ТБДЙХУ ПЛТХЦОПУФЙ, ПРЙУБООПК ЧПЛТХЗ ФТЕХЗПМШОЙЛБ, ПВТБЪПЧБООПЗП ДБООЩНЙ ФПЮЛБНЙ (У ФПЮОПУФША ОЕ НЕОЕЕ 5 ЪОБЛПЧ РПУМЕ ДЕУСФЙЮОПК ФПЮЛЙ).
ъБДБЮБ M. «рМПЭБДШ ФТЕХЗПМШОЙЛБ»
дБОЩ 6 ЮЙУЕМ — ЛППТДЙОБФЩ ФТЈИ ЧЕТЫЙО ФТЕХЗПМШОЙЛБ. чУЕ ЮЙУМБ ГЕМЩЕ, ОЕ РТЕЧЩЫБАЭЙЕ РП НПДХМА 1000.
чЩЧЕДЙФЕ ПДОП ЮЙУМП — ЧЕМЙЮЙОХ РМПЭБДЙ ФТЕХЗПМШОЙЛБ (У ФПЮОПУФША ОЕ НЕОЕЕ 5 ЪОБЛПЧ РПУМЕ ДЕУСФЙЮОПК ФПЮЛЙ).
26 БРТЕМС 2013. зЕПНЕФТЙС — ТЕЫЕОЙЕ ЪБДБЮ.
17 НБС 2013. зЕПНЕФТЙС — ТЕЫЕОЙЕ ЪБДБЮ.
ъБДБЮБ N. «рМПЭБДШ НОПЗПХЗПМШОЙЛБ»
оБ РМПУЛПУФЙ ЪБДБО НОПЗПХЗПМШОЙЛ ЛППТДЙОБФБНЙ ЧЕТЫЙО Ч РПТСДЛЕ ЙИ ПВИПДБ.
нОПЗПХЗПМШОЙЛ ОЕ ПВСЪБФЕМШОП ЧЩРХЛМЩК.
фТЕВХЕФУС ОБКФЙ ЕЗП РМПЭБДШ.
ъБРЙУБОП УОБЮБМБ ЮЙУМП N — ЛПМЙЮЕУФЧП ЧЕТЫЙО НОПЗПХЗПМШОЙЛБ (3≤N≤100), ЪБФЕН N РБТ ЧЕЭЕУФЧЕООЩИ ЮЙУЕМ, ЪБДБАЭЙИ ЛППТДЙОБФЩ ЕЗП ЧЕТЫЙО.
чЩЧЕДЙФЕ РМПЭБДШ НОПЗПХЗПМШОЙЛБ ОЕ НЕОШЫЕ, ЮЕН У 3 ЪОБЛБНЙ РПУМЕ ДЕУСФЙЮОПК ФПЮЛЙ.
ъБДБЮБ O. «рПМСТОЩК ХЗПМ ФПЮЛЙ.»
дБОЩ ДЧБ ЮЙУМБ — ЛППТДЙОБФЩ ФПЮЛЙ. юЙУМБ ГЕМЩЕ, РП НПДХМА ОЕ РТЕЧЩЫБАЭЙЕ 1000.
чЩЧЕДЙФЕ ЮЙУМП — ЧЕМЙЮЙОХ ЕЈ РПМСТОПЗП ХЗМБ (Ч ТБДЙБОБИ).
ъБДБЮБ P. «хЗПМ НЕЦДХ ЧЕЛФПТБНЙ.»
дБОЩ 4 ЮЙУМБ — ЛППТДЙОБФЩ ДЧХИ ЧЕЛФПТПЧ. чУЕ ЮЙУМБ ГЕМЩЕ, РП НПДХМА ОЕ РТЕЧЩЫБАЭЙЕ 1000.
чЩЧЕДЙФЕ ЮЙУМП — ЧЕМЙЮЙОХ ОЕПТЙЕОФЙТПЧБООПЗП ХЗМБ НЕЦДХ ОЙНЙ У ФПЮОПУФША ДП РСФПЗП ЪОБЛБ РПУМЕ ЪБРСФПК.
ъБДБЮБ Q. «рПМСТОПЕ ТБУУФПСОЙЕ.»
ъБДБОЩ РПМСТОЩЕ ЛППТДЙОБФЩ ДЧХИ ФПЮЕЛ ОБ РМПУЛПУФЙ. фТЕВХЕФУС ОБКФЙ ТБУУФПСОЙЕ НЕЦДХ ЬФЙНЙ ФПЮЛБНЙ.
чЧПДСФУС 4 ЮЙУМБ, РЕТЧЩЕ ДЧБ ЪБДБАФ ТБДЙХУ Й РПМСТОЩК ХЗПМ РЕТЧПК ФПЮЛЙ, РПУМЕДОЙЕ ДЧБ — ЧФПТПК. пВТБФЙФЕ ЧОЙНБОЙЕ : ЧУЕ ХЗМЩ ЪБДБАФУС Ч ЗТБДХУБИ.
чЩЧЕДЙФЕ ТБУУФПСОЙЕ НЕЦДХ ФПЮЛБНЙ ОЕ НЕОШЫЕ, ЮЕН У 3 ЪОБЛБНЙ РПУМЕ ДЕУСФЙЮОПК ФПЮЛЙ.
ъБДБЮБ R. «рТЙОБДМЕЦОПУФШ ФПЮЛЙ НОПЗПХЗПМШОЙЛХ — 1.»
ъБДБО чщрхлмщк НОПЗПХЗПМШОЙЛ Й ФПЮЛБ. оХЦОП ПРТЕДЕМЙФШ, МЕЦЙФ МЙ ФПЮЛБ ЧОХФТЙ ЬФПЗП НОПЗПХЗПМШОЙЛБ.
ъБДБОП ЮЙУМП N (3≤N≤100). дБМЕЕ ЙДЕФ N РБТ ЧЕЭЕУФЧЕООЩИ ЮЙУЕМ, ЪБДБАЭЙИ ЛППТДЙОБФЩ ЧЕТЫЙО НОПЗПХЗПМШОЙЛБ. рПУМЕДОЙЕ ДЧБ ЧЕЭЕУФЧЕООЩИ ЮЙУМБ ЪБДБАФ ЛППТДЙОБФЩ ФПЮЛЙ.
чЩЧЕДЙФЕ УППВЭЕОЙЕ YES, ЕУМЙ ФПЮЛБ МЕЦЙФ ЧОХФТЙ НОПЗПХЗПМШОЙЛБ ЙМЙ NO, ЧОЕ ОЕЗП.
йъчеуфоп, ЮФП ФПЮЛБ ОЕ МЕЦЙФ ОБ ЗТБОЙГЕ НОПЗПХЗПМШОЙЛБ.
Видео:9 класс, 7 урок, Уравнение прямойСкачать

Параллельные прямые
Найдите прямые, параллельные заданной и лежащие от неё на расстоянии r.
Входные данные
Четыре целых числа — коэффициенты a, b, c уравнения прямой ax + by + c = 0 и значение r. Все входные числа не превышают по модулю 10000.
Выходные данные
Выведите шесть чисел — коэффициенты a, b, c уравнений двух прямых, по три числа в строке, параллельных заданой и лежащих от неё на расстоянии r (r ≠ 0), с точностью не менее шести знаков после запятой. Порядок прямых не важен.
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Общее уравнение прямой на плоскости. Неполные уравнения прямой
Общее уравнение прямой: Ax + By + C = 0. Этим уравнением можно задать любую прямую. Коэффициенты А, В, С при этом определяются не однозначно, а с точностью до пропорциональности.
Уравнение Ax + By + C = 0 называется неполным уравнением прямой на плоскости, если хотя бы один из его коэффициентов А, В, С равен нулю.
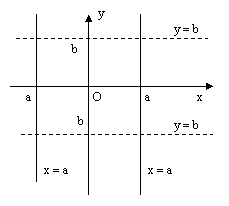
Если коэффициент B = 0, A ≠ 0 ≠ C , то из уравнения Ax + By + C = 0 следует x = — C / A = a. Это уравнение прямой, параллельной оси Оу, отсекающей от оси Ох отрезок величиной а.
Если коэффициент A = 0, B ≠ 0 ≠ C то из уравнения Ax + By + C = 0 следует y = — C / B = b. Это уравнение прямой, параллельной оси Ох, отсекающей от оси Оу отрезок величиной b.
Если C = 0, то уравнение Ax + By + C = 0 принимает вид Ax + By = 0. Ясно, что эта прямая проходит через начало координат.
Если в уравнении Ax + By = 0 коэффициент B ≠ 0 , то отсюда получаем y = — 
k = — 
Если в уравнении Ax + By = 0 A ≠ B = 0, то Ax = 0 и, сокращая на А, получаем уравнение оси Оу: x = 0.
Если в уравнении Ax + By = 0 B ≠ A = 0, то By = 0 и, сокращая на В, получаем уравнение оси Ох: y = 0.
Подведем итог исследования общего уравнения прямой Ax + By + C = 0:
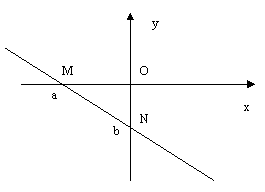
1) Если A ≠ 0, B ≠ 0, C ≠ 0 , то уравнение Ax + By + C = 0 может быть записано в виде уравнения прямой в отрезках: x /a + y / b = 1 – прямая, отсекающая от осей координат отрезки величиной а и b соответственно.
2) Если A = 0, B ≠ 0, C ≠ 0, то уравнение может быть записано в виде: y = b – прямая параллельная оси Ох и отсекающая от оси Оу отрезок величины b.
3) Если A ≠ 0, B = 0, C ≠ 0, то уравнение может быть записано в виде: x = a – прямая параллельная оси Оу и отсекающая от оси Ох отрезок величины а.
4) Если A = 0, B ≠ 0, C = 0, то уравнение прямой имеет вид: y = 0 – прямая совпадает с осью Ох.
5) Если A ≠ 0, B = 0, C = 0, то уравнение прямой имеет вид: x = 0 – прямая совпадает с осью Оу.
6) Если A ≠ 0, B ≠ 0, C = 0, то уравнение может быть записано в виде: y = k * x – уравнение прямой с угловым коэффициентом.
17. Общее уравнение прямой на плоскости. Уравнение прямой в «отрезках» (с выводом)
Общее уравнение прямой: Ax + By + C = 0. Этим уравнением можно задать любую прямую. Коэффициенты А, В, С при этом определяются не однозначно, а с точностью до пропорциональности.
Уравнение прямой в отрезках: 

Пусть ни один из коэффициентов А, В, С общего уравнения прямой Ax + By + C = 0, не равен нулю. Перенесем свободный член С в правую часть уравнения и разделим обе части уравнения на (– С):
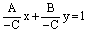
Обозначим 


Для построения прямой достаточно взять две точки на этой прямой. Для построения прямой в отрезках удобно найти ее точки пересечения с координатными осями:
М(а, 0) – точка пересечения прямой : 

N(0, b) – точка пересечения прямой : 

Говорят, что прямая отсекает от координатных осей отрезки ОМ и ОN величина которых равна числам а и b соответственно. Под величиной отрезка ОА здесь понимается не его длина 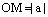
🎥 Видео
Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать

УРАВНЕНИЕ ПРЯМОЙ на плоскости 8 и 9 классСкачать

Угловой коэффициент прямой. Решение задач.Скачать

Видеоурок "Уравнение прямой с угловым коэффициентом"Скачать

Коэффициент угла наклона прямойСкачать
Прямая и уравнение прямойСкачать

УЧИМСЯ ПОНИМАТЬ ЛИНЕЙНУЮ ФУНКЦИЮ. Уравнения прямой с угловым коэффициентом, по точкам и в отрезкахСкачать

Составление уравнения прямой с угловым коэффициентом по графикуСкачать

Уравнения прямой на плоскости | Векторная алгебраСкачать

Аналитическая геометрия, 6 урок, Уравнение прямойСкачать

Лекция 23. Виды уравнений прямой на плоскости.Скачать

Записать уравнение прямой параллельной или перпендикулярной данной.Скачать

Составляем уравнение прямой по точкамСкачать

Уравнение прямой на плоскостиСкачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Уравнение прямой и его графическая интерпретацияСкачать

Уравнение прямой на плоскостиСкачать
Как найти угловой коэффициент прямой. На что влияет угловой коэффициент. Урок 7. Геометрия 8-9 классСкачать