Условие
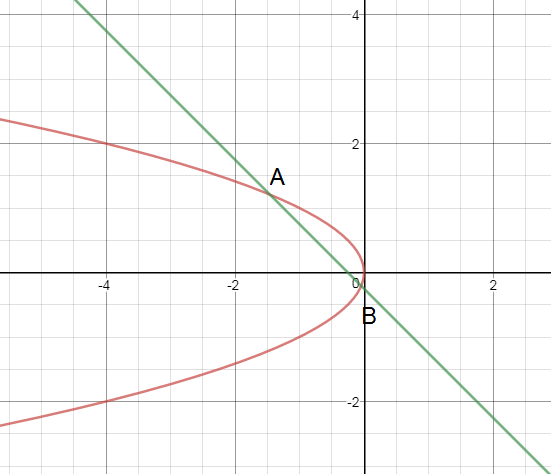
5) Через фокус параболы у^2 = -x проведена прямая под углом 135° к оси Ох. Найти длину образовавшейся хорды.
Решение
Каноническое уравнение параболы имеет вид
y^2=2px
2p=-1
p=-1/2
Координаты фокуса параболы — точки F(-1/4;0)
Уравнение прямой под углом 135 градусов к оси, это уравнение прямой с угловым коэффициентом k=tg135 градусов =-1
имеет вид
у=-х+b
Чтобы найти b подставим координаты точки F в это уравнение
0=-(-1/4)+b
b=-1/4
Найдем координаты точек пересечения прямой у =-х — (1/4) с параболой y^2=-x
(-x-(1/4))^2=-x
x^2+(x/2)+(1/16)=-x
x^2+3x/2+(1/16)=0
16x^2+24x+1=0
D=(24)^2-4*16=576-64=512
x1=(-24-16sqrt(2))/32 или x2=(-24+16sqrt(2))/32
x1=(-3-2sqrt(2))/4 или x2=(-3+2sqrt(2))/4
y1=(2+2sqrt(2))/4 или y2=(2-2sqrt(2))/4
|AB|=sqrt(4)=2
Видео:Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Контрольная работа
КРИВЫЕ ВТОРОГО ПОРЯДКА
В ответах к задачам 2 и 3 записать название кривой и ее каноническое уравнение. В задаче 2 привести координаты центра для эллипса и гиперболы или координаты вершины для параболы.
1. Составить каноническое уравнение гиперболы, фокусы которой расположены на оси Ox симметрично относительно начала координат, если 2a = 16,
Привести к каноническому виду уравнение кривой:
1. Фокусы эллипса, проходящего через точку P(8; 18/5), расположены на оси Ox симметрично относительно начала координат. Малая полуось равна 6. Составить уравнения прямых, проходящих через точку P и его фокусы.
Привести к каноническому виду уравнение кривой:
1. Найти расстояние фокуса гиперболы 
Привести к каноническому виду уравнение кривой:
1. Через фокус параболы y2 = — 4x проведена прямая под углом 120° к оси Ox. Написать уравнение прямой.
Привести к каноническому виду уравнение кривой:
1. Написать каноническое уравнение гиперболы, зная, что расстояние одной из ее вершин от фокусов равны 9 и 1.
Привести к каноническому виду уравнение кривой:
1. Эксцентриситет эллипса равен 
Привести к каноническому виду уравнение кривой:
1. Фокусы гиперболы, проходящей через точку (8; 3
Привести к каноническому виду уравнение кривой:
1. Дана парабола y2 = 6x. Через точку (4; 1) проведена хорда, которая делится пополам в этой точке. Найти уравнение этой хорды.
Привести к каноническому виду уравнение кривой:
1. Найти каноническое уравнение гиперболы, фокусы которой совпадают с фокусами эллипса 
Привести к каноническому виду уравнение кривой:
1. Составить уравнение эллипса, фокусы которого расположены на оси Ox
симметрично относительно начала координат, если 2c = 6, e = 3/5.
Привести к каноническому виду уравнение кривой:
2. y2 — 3x — 10y + 31 = 0. 3. 4x2 — 2
Видео:213. Фокус и директриса параболы.Скачать

Кривые второго порядка на плоскости
Уравнение вида Ах 2 +2Вху+Су 2 +2Dх+2Еу+F=0 называется общим уравнением кривой второго порядка. Коэффициенты уравнения – действительные числа, причем хотя бы одно из чисел А,В,С отлично от нуля. Такое уравнение определяет на плоскости окружность, эллипс, гиперболу или параболу.
В табл. 2 приведены уравнения кривых второго порядка и определен смысл входящих в них коэффициентов.
| № п/п | Определение кривой | Вид уравнения | Примечание | |||||
 Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная (рис.4) Эллипс – множество всех точек плоскости, сумма расстояний от которых до двух точек, называемых фокусами, есть величина постоянная (рис.4) |  — каноническое уравнение эллипса — каноническое уравнение эллипса | 2а – большая ось; 2b – малая ось 2с–межфокус-ное расстояние с 2 =а 2 -b 2 ; 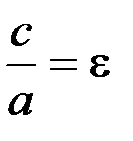 — эксцентриси-тет, 0 2 =а 2 +b 2 ; — эксцентриси-тет, 0 2 =а 2 +b 2 ; 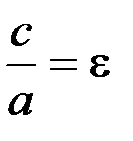 — эксцентри-ситет, e>1. Точки А1,А2 – вершины гиперболы. Прямые — эксцентри-ситет, e>1. Точки А1,А2 – вершины гиперболы. Прямые 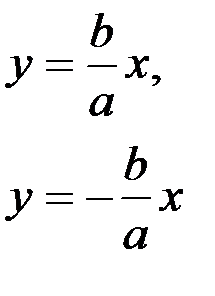 — асимптоты — асимптоты | ||||||
| 3. | Парабола — множество точек плоскости, каждая из которых одинаково удалена от данной точки, называемой фокусом, и данной прямой, называемой директриссой.
| у 2 =2px – каноническое уравнение параболы, симметричной относительно оси ОХ x 2 =2pу – каноническое уравнение параболы, симметричной относительно оси ОY (рис.6б) | F  — фокус, — фокус, 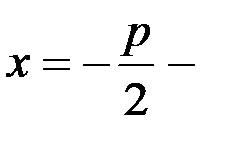 ди-ректриса. Точка (0;0) – вершина параболы (рис.6а) F ди-ректриса. Точка (0;0) – вершина параболы (рис.6а) F  — фокус, — фокус,  ди-ректриса. Точка (0;0) – вершина параболы (рис.6б) ди-ректриса. Точка (0;0) – вершина параболы (рис.6б) |
1. Найти координаты фокусов и эксцентриситет эллипса 36х 2 +100у 2 =3600.
Приведем уравнение эллипса к каноническому виду:
36х 2 +100у 2 =3600, поделим обе части уравнения на 3600:

С= 
Эксцентриситет: 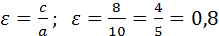
Ответ: Fл(-8,0); Fп(8,0); 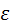
2.Написать уравнение прямой, проходящей через левую вершину эллипса 16х 2 +25у 2 =400 и точку М0(1;-3) (рис.7).
| у |
Решение:
| -4 |
| -5 |
| М |
| х |
| М0 |
| Рис. 7 |
Приведем уравнение 16х 2 +25у 2 =400 к каноническому виду.
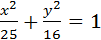
Левая вершина эллипса (-а,0)Þ(-5,0). Обозначим М(-5,0). Составим уравнение прямой, проходящей через точки М0 и М:
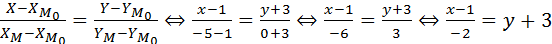
Ответ: 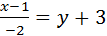
3. Написать уравнение прямой, проходящей через правый фокус гиперболы 9х 2 -16у 2 =144 и параллельно прямой 3х-2у+6=0 (рис.8).
| -3 |
| -4 |
| FП |
 |
| х |
| у |
| Рис.8 |
Приведем уравнение 9х 2 -16у 2 =144 к каноническому виду 
Правый фокус гиперболы Fп(с,0);
С= 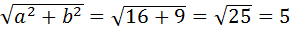
Пусть уравнение искомой прямой имеет вид y=k2x+b2;
Значит, y=(3/2)x+b2 проходит через точку Fп(5,0), то 0=(3/2)5+b2Þb2=-15/2. Итак, 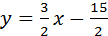
Искомая прямая проходит через точку Fл(5,0) параллельно прямой 3х-2у+6=0. Из общего уравнения заданной прямой определяем вектор нормали 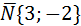
4. Написать уравнение прямой l, проходящей через нижнюю вершину эллипса 4х 2 +20у 2 =80, перпендикулярно прямой 2х—у+1=0 (рис.9).
| М |
 |
| -2 |
| y |
 |
| l |
| х |
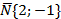 |
| Рис. 9 |
Приведем уравнение к каноническому виду 4х 2 +20у 2 =80,
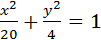
Нижняя вершина имеет вид: М(0;-b)=М(0;-2).
Условие перпендикулярности двух прямых: k1k3=-1.
k2=-1: k1Þk2=-1/2,
Так как прямая 

Итак, 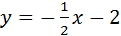
По условию задачи требуется написать уравнение прямой l, проходящей через точку М(0;-2) перпендикулярно прямой 2х—у+1=0. Из общего уравнения прямой определяем координаты вектора нормали 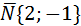
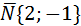
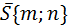

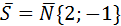

5. Написать уравнение прямой, проходящей через правый фокус эллипса 
Правый фокус эллипса имеет вид Fп(с,0);
С= 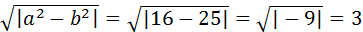
Так как прямая проходит под углом 45˚ к оси Ох, то k=tgα=tg45˚=1.
Пусть уравнение искомой прямой имеет вид: y=kx+b;
Так как прямая проходит через точку Fп(3,0), то 0=3+bÞb=-3.
Плоскость в пространстве
Любое уравнение первой степени в трехмерном пространстве определяет какую-либо плоскость.
Разным способам задания плоскости соответствуют различные виды уравнений (табл. 3.)
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
| Уравнение плоскости, проходящей через данную точку перпендикулярно заданному вектору А(х-х0)+В(у-у0)+С(z-z0)=0 | (x0,y0,z0) – координаты заданной точки; АВС – координаты заданного вектора | Вектор N(А,В,С) называется нормальным вектором плоскости | |
| Общее уравнение плоскости Ах+Ву+Сz+D=0 | D=-Ax0-By0-Cz0, АВС – нормальный вектор плоскости; | Это уравнение получается из уравнения (1) эле-ментарными | |
| № п/п | Вид уравнения | Смысл входящих в уравнение коэффициентов | Примечание |
| х0,y0,z0 – координаты данной точки | преобразованиями | ||
Уравнение плоскости, проходящей через три заданные точки 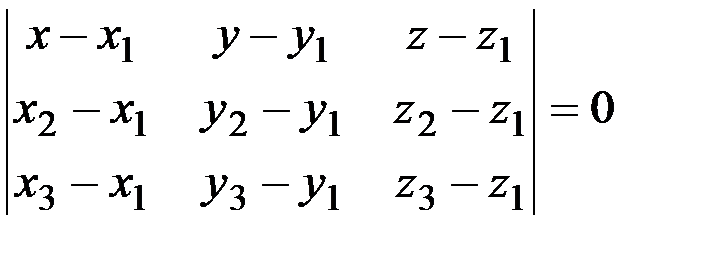 | М1(х1,y1,z1), М2(х2,y2,z2), М3(х3,y3,z3) – три точки, заданные своими координатами | Точки М1, М2, М3 не должны лежать на одной прямой | |
Уравнение плоскости в отрезках на осях 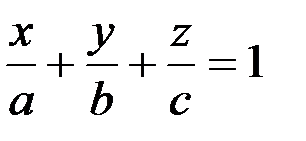 | а,b,c – отрезки, отсекаемые плоскостью от осей координат | аbc≠0 |
Пусть даны две плоскости a1 и a2:
Угол между двумя плоскостями определяется как 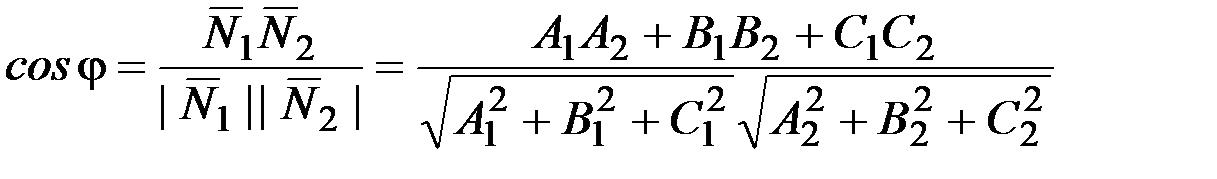
Условие перпендикулярности двух плоскостей:
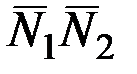
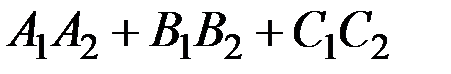
Условие параллельности двух плоскостей:


Расстояние от точки до плоскости:
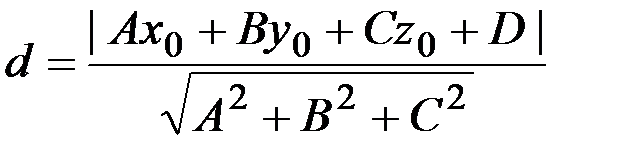
📹 Видео
9 класс, 7 урок, Уравнение прямойСкачать

Реакция на результаты ЕГЭ 2022 по русскому языкуСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Угловой коэффициент прямой. Решение задач.Скачать

Уравнение прямой в пространстве через 2 точки. 11 класс.Скачать

Уравнение прямой.Скачать

Линейная функция. Составить уравнение прямой проходящей через точку и перпендикулярно прямой.Скачать

Фокус и директриса параболы 2Скачать

§25 Исследование канонического уравнения параболыСкачать

Уравнение параллельной прямойСкачать

Фокус и директриса параболы 1Скачать

Вычисление фокуса параболыСкачать

Как написать уравнение параболы с помощью графикаСкачать

10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Как легко составить уравнение параболы из графикаСкачать

Видеоурок "Уравнение прямой, проходящей через две точки"Скачать

Как определить уравнение параболы по графику?Скачать