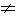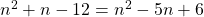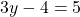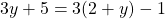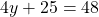Знак равенства используется в математике очень часто, и смысл, который придается этому знаку, далеко не всегда один и тот же. Так, часто мы соединяем знаком равенства два числа, например:
1370 = 3 2 ·5·31 (1) ;
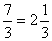
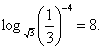
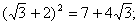
Каждая такая запись представляет собой некоторое высказывание, которое может быть истинным или ложным. Среди приведенных выше четырех высказываний такого рода второе, третье и четвертое являются истинными, а первое — ложным.
Для того чтобы убедиться в истинности (или ложности) такого высказывания, нередко бывает нужно произвести те или иные действия: сложение дробей, разложение на множители, возведение суммы двух чисел в квадрат и т. п. Однако смысл знака равенства во всех этих случаях один и тот же: истинность такого высказывания означает, что слева и справа от знака равенства стоит одно и то-же число (только, может быть, записанное по-разному).
Высказывания такого вида мы будем называть числовыми равенствами. Если некоторое числовое равенство представляет собой истинное высказывание, то для краткости говорят: «это — верное равенство». Так, равенство (2) — верное. Если же некоторое числовое равенство представляет собой ложное высказывание, то для краткости говорят: «это—неверное равенство». Так, (1) —неверное равенство.
В ином смысле применяется знак =, когда идет речь о равенстве функций. Напомним, что две функции f (х) и g (х) считаются равными (т. е. совпадающими), если, во-первых, области определения этих двух функций совпадают и, во-вторых, для любого числа х0, принадлежащего общей области определения этих функций, значения функций в точке х0 совпадают, т. е. верно числовое равенство f (х0) = g(x0). Равенство функций (х) и g(x) обычно выражают записью f(x) = g(x).
Например, мы пишем (х 2 + 1) 6 = х 3 + Зx 4 +. Зx 2 + 1, выражая этой записью тот факт, что слева и справа от знака = стоят равные функции (т. е. слева и справа стоит одна и та же функция, только, может быть, записанная по-разному).
В записи, выражающей равенство (т. е. совпадение) двух функций, вместо знака = часто используют знак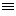
Запись f(x)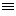
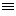
Подчеркнем еще раз: когда мы говорим, что f(x) = g(x) есть тождество, то это означает, что области определения функций f(х) и g(х) совпадают и при этом для любого х0, принадлежащего этой области определения, справедливо числовое равенство f(x0) = g(x0).
Примерами тождеств могут служить соотношения:
(x + 1) 2 = x 2 + 2x + 1,
sin 2 x= 1 — cos 2 x.
Иногда при рассмотрении тождеств приходится ограничивать области определения функций. Именно, будем говорить, что равенство f(x) = g(x) является тождеством на множестве М, если, во-первых, множество М содержится в области определения каждой из функций f(x), g (х) и, во-вторых, для любого числа х0, принадлежащего множеству М, справедливо числовое равенство f(x0) = g (x0) В этом случае пишут:
. Пример 1. Равенство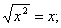
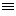

Заметим, что обе функции y=
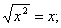
Пример 2. Рассмотрим равенство arcsin(sinx) =





(z + 7) 2 = z 2 — 14z + 49,
(а — 1)(а 2 + а + 1) = а 3 — 1
являются тождествами на множестве всех действительных чисел (или даже на множестве всех комплексных чисел), Можно также рассматривать функции, зависящие от двух или большего числа аргументов, и писать тождества для таких функций. Конечно, и в этом случае надо указывать, при каких значениях аргументов написанное равенство является тождеством.
Например, равенство log2 a b = b log2 a является тождеством при а > 0 и любом действительном b; равенство
является тождеством при x





Мы рассмотрели два случая использования знака = в алгебре: для записи числовых равенств и для записи тождеств (в последнем случае он иногда заменяется знаком ?. В совершенно ином смысле используется знак = при рассмотрении уравнений. Уравнение с одним неизвестным х в общем случае записывается в виде
где f(х) и g(x) — произвольные функции, Таким образом, по внешнему виду уравнение выглядит так же, как и тождество: две функции, соединенные знаком равенства. Но когда мы говорим, что соотношение (5) есть уравнение, то это показывает наше отношение к этому равенству. Именно, когда мы говорим, что (5) есть уравнение, то это означает, что равенство (5) рассматривается как неопределенное высказывание (при одних значениях х истинное, при других—ложное), и мы интересуемся нахождением корней этого уравнения, т. е. таких значений х, при подстановке которых это неопределенное высказывание становится истинным. Более подробно, корнем (или решением) уравнения называется всякое число, при подстановке которого вместо неизвестного в обе части уравнения получается справедливое (верное) числовое равенство. Но что значит «получается справедливое числовое равенство»? Это означает, во-первых, что при подстановке этого числа вместо неизвестного все действия, обозначенные в левой и правой частях уравнения, оказываются выполнимыми и, во-вторых, в результате выполнения этих действий в левой и правой частях получается одно и то же число. Иначе говоря, число а называется корнем уравнения (5), если, во-первых, это число принадлежит как области определения функции f(x), так и области определения функции g(x) и, во-вторых, значения этих функций в точке а совпадают, т. е.
f(a) = g<a).
Итак, если сказано, что равенство (5) рассматривается как уравнение, то это означает, что мы интересуемся нахождением корней этого уравнения, т. е. тех значений, которые обращают соотношение (5) в верное числовое равенство.
Пример 3. Для уравнения (х — 1) 2 = х 2 — 2x + 1 любое действительное число b является корнем, так как равенство (b — 1) 2 = b 2 — 2b + 1 имеет место для любого действительного числа b.
Пример 4. Если рассматривать уравнение |х| = х на множестве всех действительных чисел, то всякое неотрицательное число является корнем этого уравнения (других корней нет).
Пример 5. Уравнение lgx = 1g( — х) не имеет решений, так как левая часть этого уравнения определена при положительных значениях х, а правая — при отрицательных, т. е. области определения левой и правой частей не имеют общих точек.
Пример 6. Уравнение cosx = 2 не имеет решений на множестве действительных чисел, так как |cosx0|
Пример 7. Уравнение х 2 = -1 не имеет решений намножестве действительных чисел и имеет два решения, x = i и х = -i., на множестве комплексных чисел.
Если найдена некоторая совокупность значений х, каждое из которых является корнем уравнения f (x)=g(x), то это еще не значит, что мы решили уравнение.
Решить уравнение — значит найти все его решения (или доказать, что уравнение не имеет решений).
Пример 8. Равенство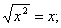
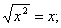
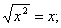
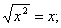
Пример 9. Бессмысленно ставить вопрос, является ли соотношение 0·x + 5 = 5 тождеством или уравнением. Мы можем сказать, что оно является тождеством на множестве всех действительных чисел. Но мы можем также рассматривать это соотношение как уравнение и тогда скажем, что корнями этого уравнения являются все действительные числа.
Замечание. Кроме рассмотренных выше случаев использования знака = в математике встречаются и другие. Так, выражение вида «рассмотрим функцию f(x) = x 3 — Зх 2 + 5x + 11» часто используется в качестве определения. В этом случае знак = имеет тот смысл, что всюду в проводимом рассуждении f (х) будет обозначать именно эту функцию.
Видео:Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать

Что такое числовые выражения, равенства, неравенства и уравнения
Выражение
Числовое выражение — это числа, соединённые знаками арифметических действий: сложение, вычитание, умножение и деление.
Найти значение числового выражения — это значит выполнить все указанные арифметические действия и получить конкретное число.
Кроме арифметических действий выражения могут содержать скобки, которые влияют на порядок действий при решении выражения.
Пример 1:
- 2 • 5 — 3 — числовое выражение
- 7 — значение числового выражения.
Равенство
Равенства — это числа или выражения, соединённые знаком = (равно).
Равенство считается верным, если числа или числовые выражения слева и справа от знака =, имеют равное значение.
Равенство считается неверным, если числа или числовые выражения слева и справа от знака =, не равны (≠).
При решении равенств соблюдается следующий порядок действий:
- надо найти значение выражения слева от знака =, действуя по правилам выполнения действий в числовых выражениях;
- надо найти значение выражения слева от знака =, действуя по правилам выполнения действий в числовых выражениях;
- надо сравнить полученные значения и сделать вывод.
Пример 2:
1) 5 = 7 — равенство неверно, так как 5 ≠ 7.
2) 36 : 2 = 6 • 3 — равенство верно, так как:
3) 48 + 9 = 54 — 1 — равенство неверно, так как:
Неравенство
Неравенства — это числа или числовые выражения соединённые знаком > (больше) или (больше), то значение выражения слева должно быть больше, чем значение выражения справа;
Пример 3:
1) 5 > 7 — неравенство неверно, так как 5
3) 4 + 5 • 6 > (4 + 5) • 6 — неравенство неверно, так как:
- 4 + 5 • 6 = 4 + 30 = 34
- (4 + 5) • 6 = 9 • 6 = 36
- 34
Уравнение
Уравнение — это равенство, которое содержит неизвестное число, обозначенное какой-либо латинской буквой: x, y, a, b, z, d и т.д.
Корень уравнения — это число, при подставлении котрого вместо буквы в равенство делает это равенство верным.
Решить уравнение — это значит найти все возможные корни уравнения.
Порядок и правила решения уравнений зависят от того, к какому типу они относятся:
Видео:ЛИНЕЙНЫЕ УРАВНЕНИЯ - Как решать линейные уравнения // Подготовка к ЕГЭ по МатематикеСкачать

Тождество — что это такое в математике
Очень часто в математике встречаются такие слова «тождество», «тождественно равные», «тождественное преобразование». Многие учащиеся путают значения этих слов. Давайте с вами разберемся, что означают эти слова.
В математике и, в более общем плане, в научных областях тождество — это открытие, что два математических объекта (имеющих два разных математических сценария) на самом деле являются одним и тем же объектом. В частности, тождество — это равенство между двумя выражениями, которое истинно независимо от значений различных используемых переменных. Тождества обычно используются для преобразования одного математического выражения в другое, особенно для решения уравнения.
Видео:Математика 1 класс (Урок№11 - Равенство. Неравенство. Знаки «больше», «меньше», «=».)Скачать

Определение тождества
Равенство, которое является верным при любом значении, входящей в него переменной, называется тождеством. Тождество, как и уравнение, имеет переменную — x, y или любую другую букву. Разница между тождеством и уравнением заключается в том, что уравнение имеет корень — то есть значение переменной, при которой выполняется данное равенство. А в тождестве равенство должно выполняться при любом значении переменной. То есть, равенство не всегда будет тождеством.
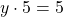
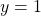
А равенство 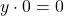
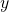
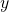
Пример: 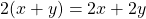
Видео:Как решать дробно-рациональные уравнения? | МатематикаСкачать

Уравнение или тождество
Как и уравнение, тождество имеет переменную. Уравнение содержит вопрос: при каких значениях переменной получается равенство. Тождество — это утверждение в том, что равенство верно при любом значении переменной.
Определите, где в перечисленных ниже выражениях будет тождество, а где только уравнение.
Вы увидите, что все выражения, кроме третьего, являются уравнениями. А тождество у нас получается только в третьем выражении, так как при раскрытии скобок в правой части уравнения, мы получаем взаимоуничтожение переменных в правой и левой частях равенства, которое остается верным.
Очень часто тождества используются в тригонометрии. Вы можете посмотреть статью на эту тему подробнее: тригонометрические тождества часть 1 и тригонометрические тождества часть 2.
Например, самое известное, так называемое основное тригонометрическое тождество:
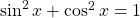
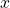
Некоторые алгебраические тождества квалифицируются как «замечательные» и позволяют облегчить вычисление или факторизацию полиномиальных выражений.
Например, замечательное тождество 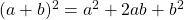

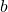
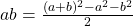
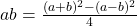
То есть, умножение осуществлялось с помощью вычитания квадратов чисел — для этого у вавилонян имелись таблицы квадратов чисел.
А еще вы можете ознакомиться с основным логарифмическим тождеством. Удачи при изучении математики.
📸 Видео
Признаки равенства треугольников | теорема пифагора | Математика | TutorOnlineСкачать

Чем ОДЗ отличается от дополнительного условия. Задание 5 ЕГЭ профиль. Иррациональное уравнениеСкачать

Математика 2 класс (Урок№26 - Уравнение. Решение уравнений подбором неизвестного числа.)Скачать

Числовые равенства. 6 класс.Скачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Математика 1 класс: видео урок 28 - равенства и неравенства (практика)Скачать

РавенствоСкачать

Решение простых уравнений. Что значит решить уравнение? Как проверить решение уравнения?Скачать

Признаки равенства треугольников. 7 класс.Скачать

Равенство. Неравенство. Выражение. УравнениеСкачать

Первый признак равенства треугольников. 7 класс.Скачать

Как решают уравнения в России и СШАСкачать

1 класс. Математика. Равенства и неравенства.Скачать

Что такое параметр? Уравнения и неравенства с параметром. 7-11 класс. Вебинар | МатематикаСкачать

Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать

СУПЕР ЛАЙФХАК — Как решать Иррациональные УравненияСкачать