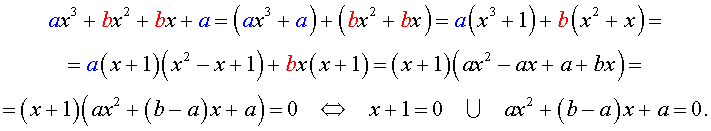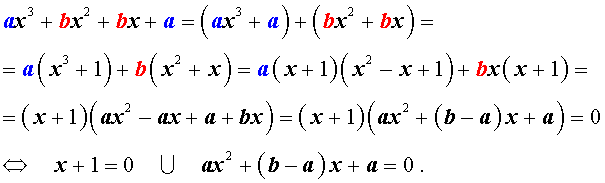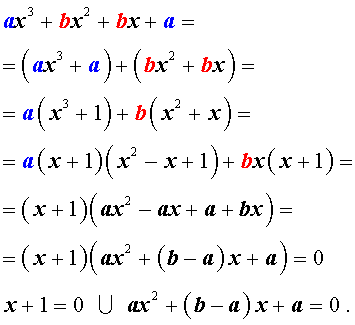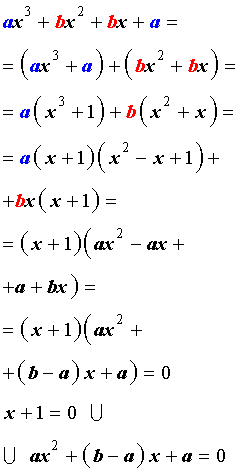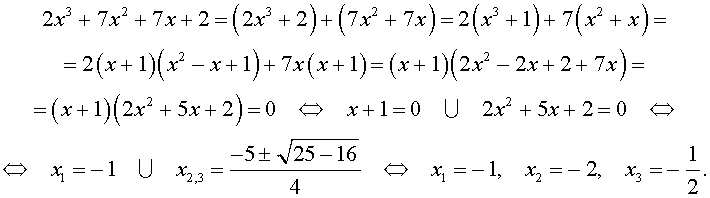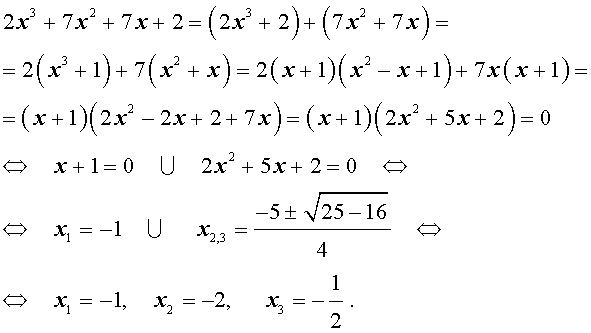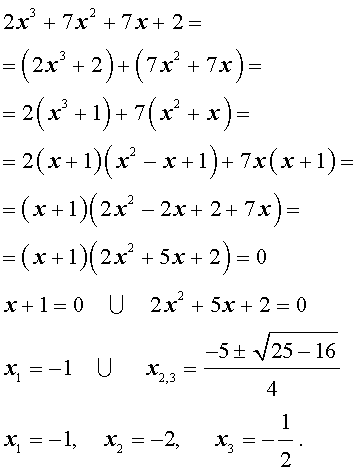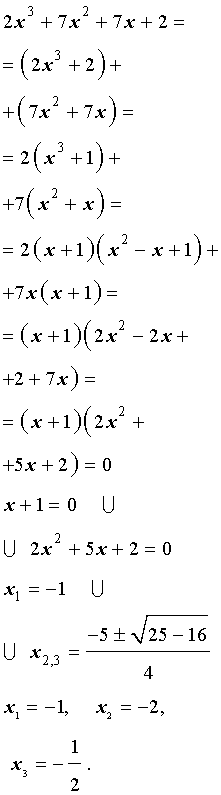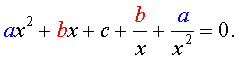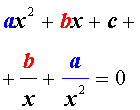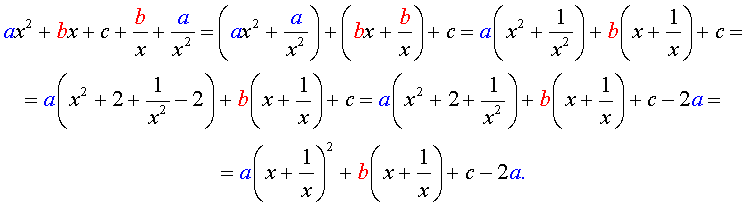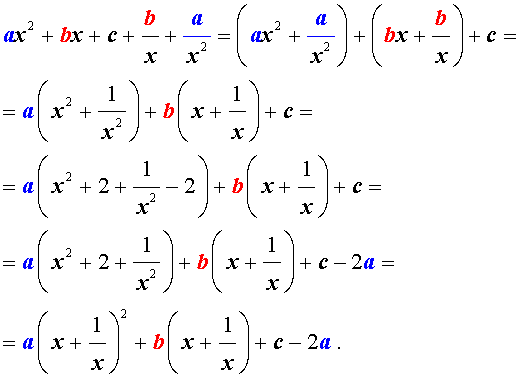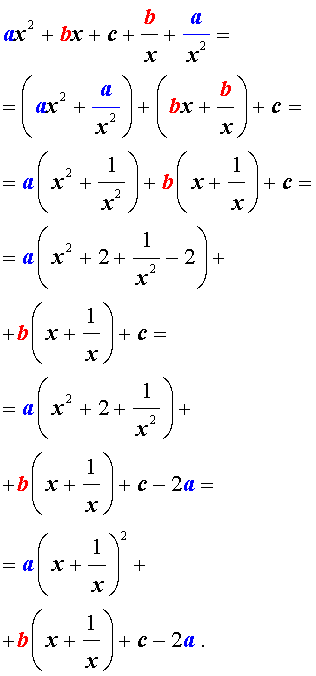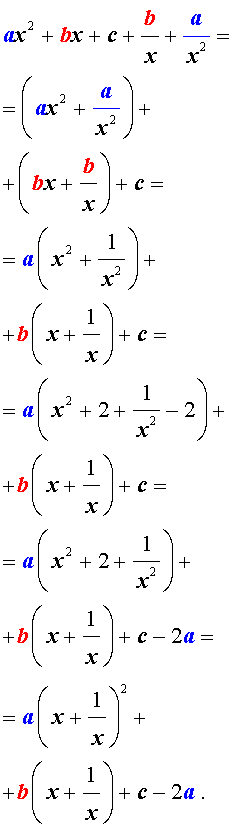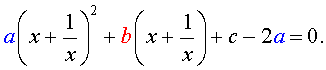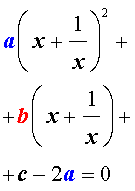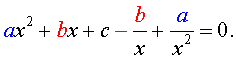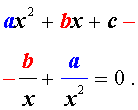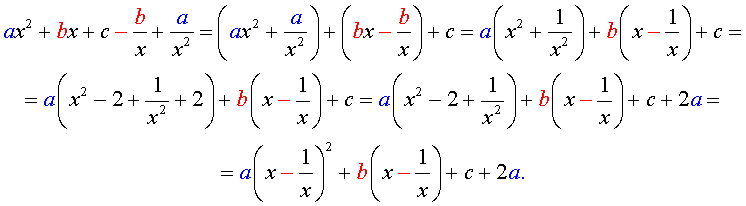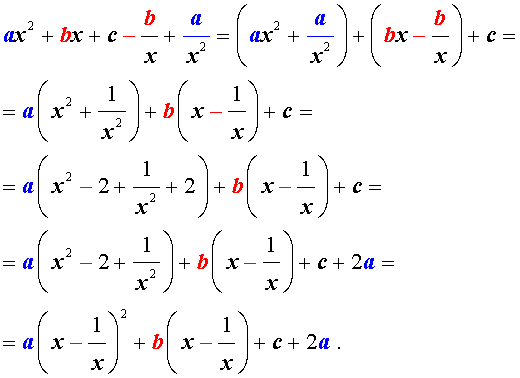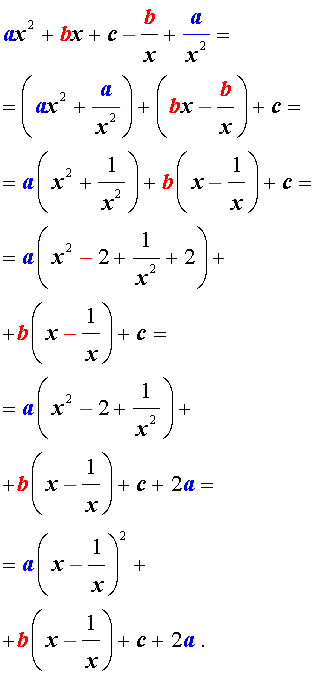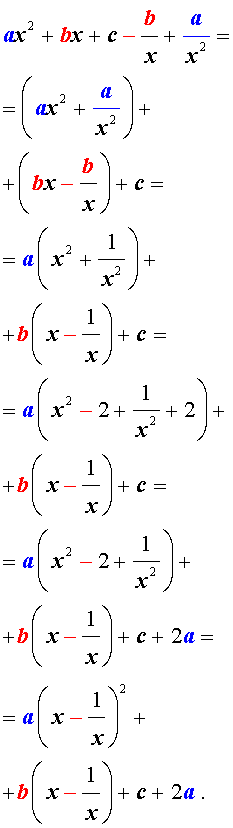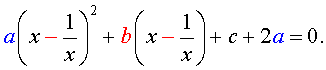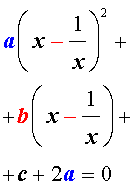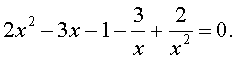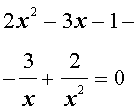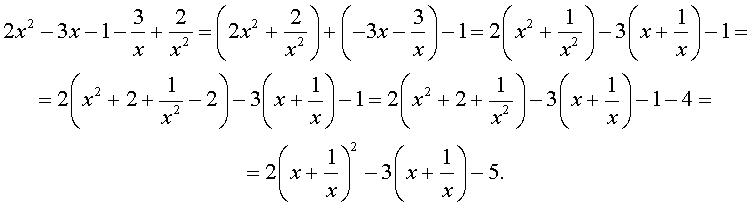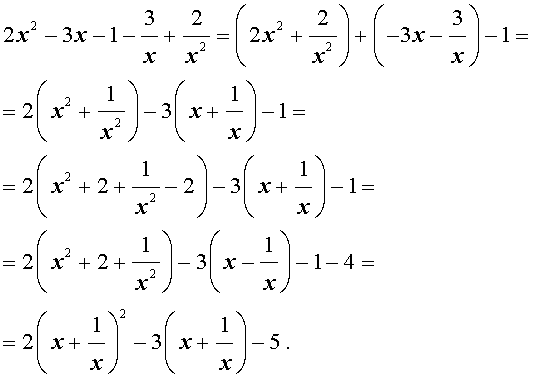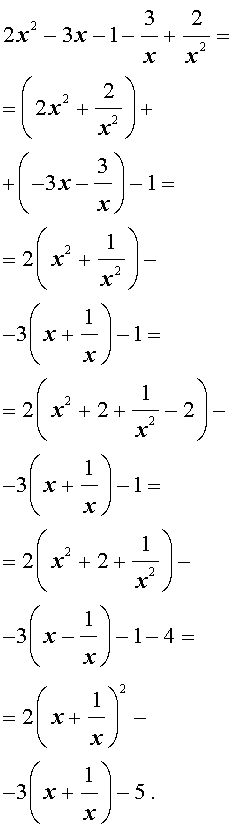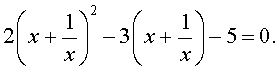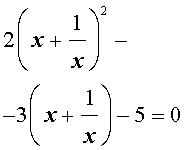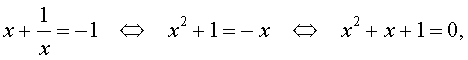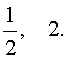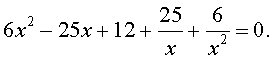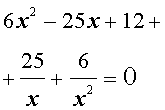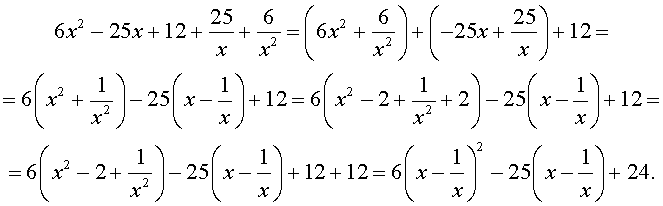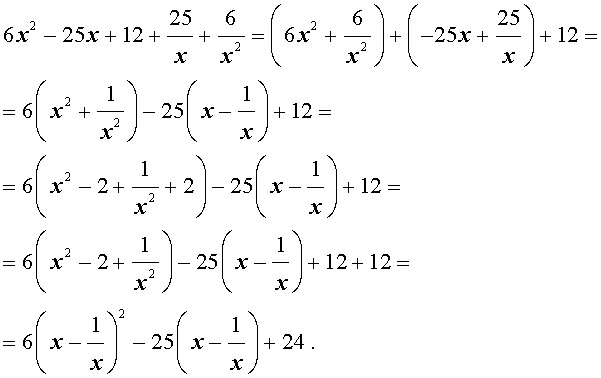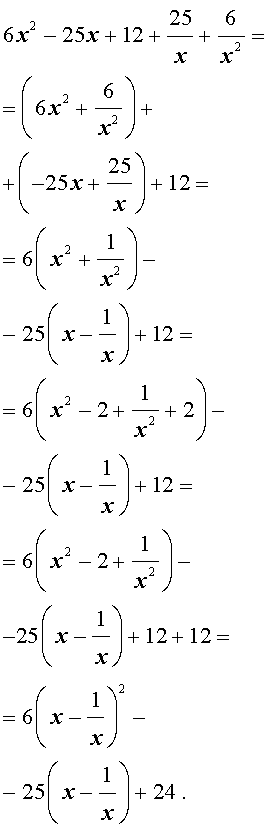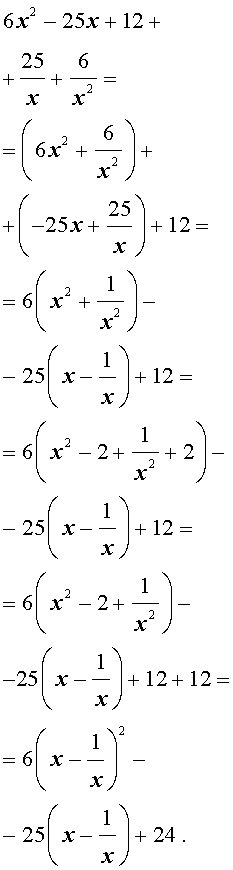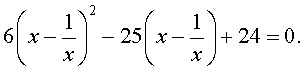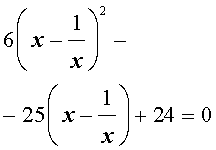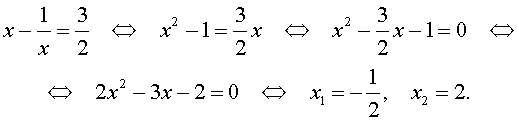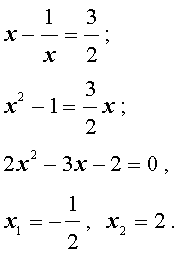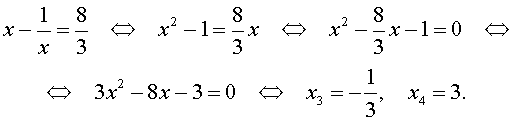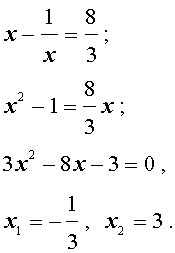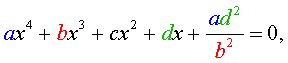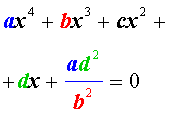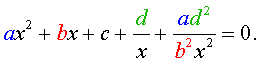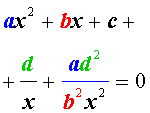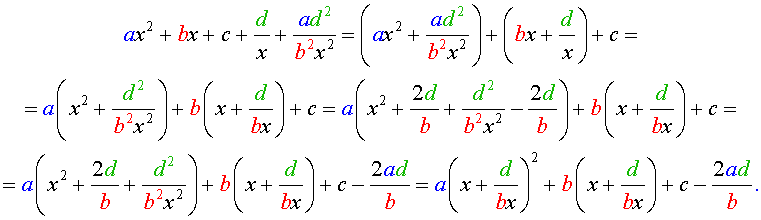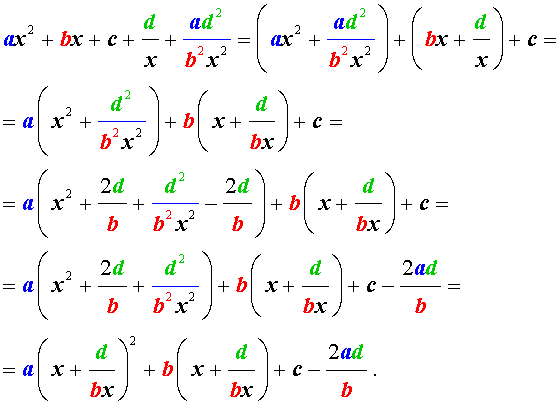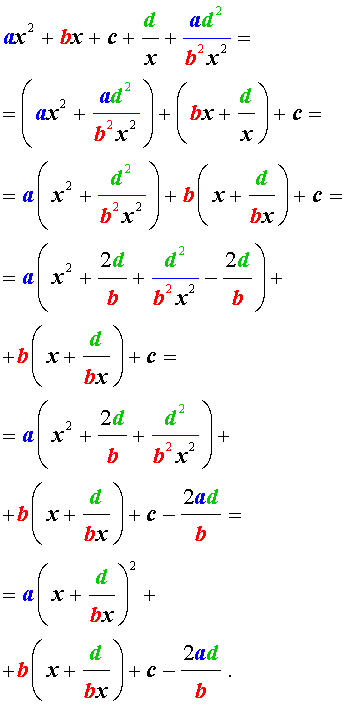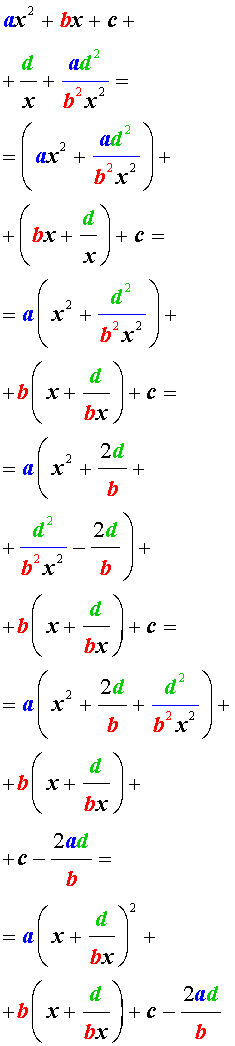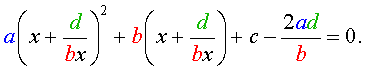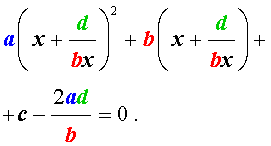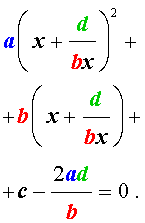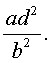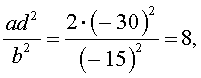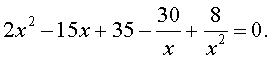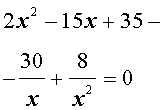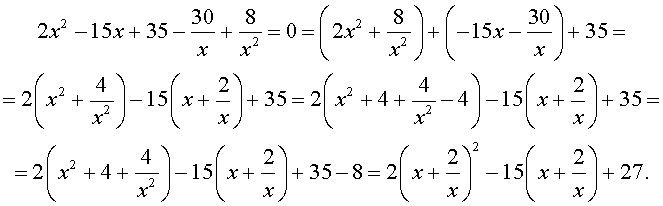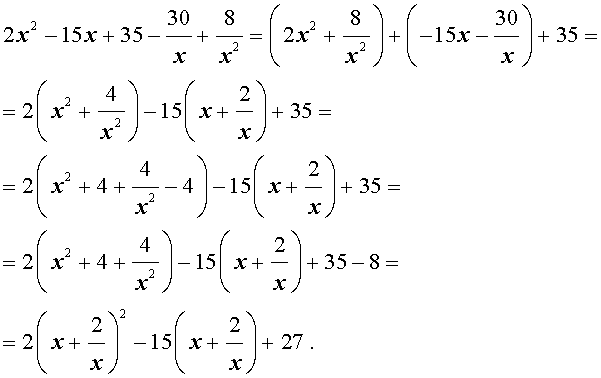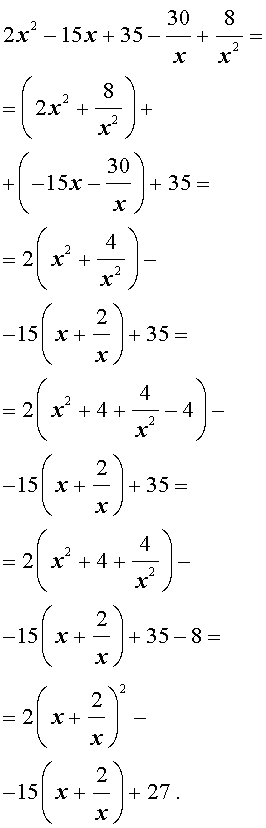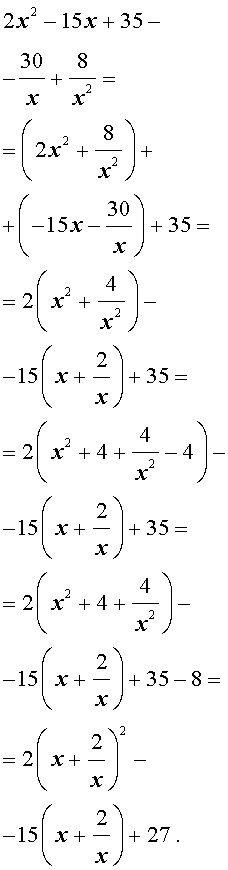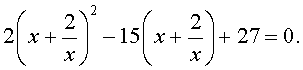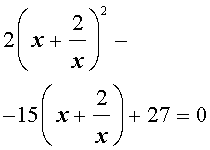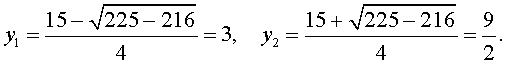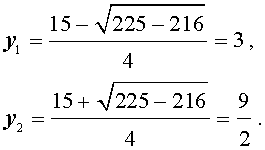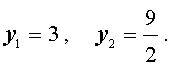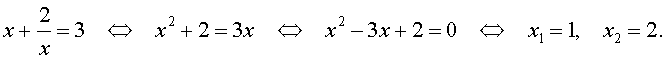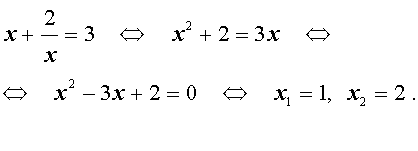возвратные (симметричные) уравнения
Существует ряд уравнений, которые удается решить при помощи сведения их к квадратным уравнениям.
К таким уравнениям, в частности, относятся уравнения следующих типов:
 | Трёхчленные уравнения |
 | Уравнения 4-ой степени, левая часть которых равна произведению четырёх последовательных членов арифметической прогрессии |
 | Возвратные (симметричные) уравнения 3-ей степени |
 | Возвратные (симметричные) уравнения 4-ой степени |
 | Обобщенные возвратные уравнения 4-ой степени |
Замечание . Уравнения, носящие название «Биквадратные уравнения» , относятся к типу «Трехчленные уравнения» .
- Возвратные (симметричные) уравнения 3-ей степени
- Возвратные (симметричные) уравнения 4-ой степени
- Обобщенные возвратные уравнения 4-ой степени
- Чем отличаются возвратные уравнения от симметричных
- ТЕМА «СИММЕТРИЧЕСКИЕ И ВОЗВРАТНЫЕ УРАВНЕНИЯ» элективный курс по алгебре (10 класс) по теме
- Скачать:
- Предварительный просмотр:
- По теме: методические разработки, презентации и конспекты
- 💡 Видео
Видео:Симметрические уравненияСкачать

Возвратные (симметричные) уравнения 3-ей степени
Возвратным уравнением 3-ей степени называют уравнение вида
| a x 3 + b x 2 + b x + a = 0, | (1) |
где a , b – заданные числа.
Решение уравнения (1) осуществляется при помощи разложения левой части уравнения (1) на множители:
Для завершения решения уравнения (1) остаётся лишь решить квадратное уравнение
Пример 1 . Решить уравнение
| 2x 3 + 7x 2 + 7x + 2 = 0. | (2) |
Решение . Разложим левую часть уравнения (2) на множители:
Ответ :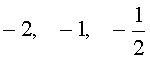
Видео:14 Урок Симметрические и возвратные уравненияСкачать

Возвратные (симметричные) уравнения 4-ой степени
Возвратными (симметричными) уравнениями 4-ой степени называют уравнения вида
| a x 4 + b x 3 + cx 2 + + b x + a = 0, | (3) |
а также уравнения вида
| a x 4 + b x 3 + cx 2 – – b x + a = 0, | (4) |
Для того, чтобы решить возвратное уравнение (3), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (5):
В результате этого преобразования уравнение (5) принимает вид
Если теперь обозначить
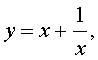 | (7) |
то уравнение (6) станет квадратным уравнением:
| a y 2 + b y + c – 2 a = 0. | (8) |
Найдем корни уравнения (8), а после этого, подставив каждый из найденных корней в равенство (7), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (3) завершено.
Для того, чтобы решить возвратное уравнение (4), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (9):
В результате этого преобразования уравнение (9) принимает вид
Если теперь обозначить
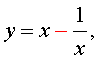 | (11) |
то уравнение (10) станет квадратным уравнением:
| a y 2 + b y + c + 2 a = 0. | (12) |
Найдем корни уравнения (13), а после этого, подставив каждый из найденных корней в равенство (11), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (4) завершено.
Пример 2 . Решить уравнение
| 2x 4 – 3x 3 – x 2 – – 3x + 2 = 0. | (13) |
Решение . Уравнение (13) является возвратным и относится к виду (3). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (14):
В результате этого преобразования уравнение (14) принимает вид
Если теперь обозначить
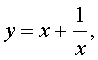 | (16) |
то уравнение (15) станет квадратным уравнением:
| 2y 2 – 3y – 5 = 0. | (17) |
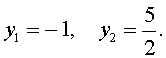 | (18) |
В первом случае из равенства (16) получаем уравнение:
которое решений не имеет.
Во втором случае из равенства (16) получаем:
Ответ :
Пример 3 . Решить уравнение
| 6x 4 – 25x 3 + 12x 2 + + 25x + 6 = 0. | (19) |
Решение . Уравнение (19) является возвратным и относится к виду (4). Разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (20):
В результате этого преобразования уравнение (20) принимает вид
Если теперь обозначить
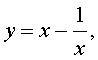 | (22) |
то уравнение (21) станет квадратным уравнением:
| 6y 2 – 25y + 24 = 0. | (23) |
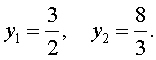 | (24) |
В первом случае из равенства (22) получаем:
Во втором случае из равенства (22) получаем:
Ответ :
Видео:Как решать возвратные уравнения?Скачать

Обобщенные возвратные уравнения 4-ой степени
Обобщенным возвратным уравнением 4-ой степени назовём уравнение вида
где a , b , c, d – заданные числа.
Для того, чтобы решить уравнение (25), разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (26):
В результате этого преобразования уравнение (26) принимает вид
Если теперь обозначить
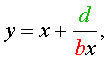 | (28) |
то уравнение (27) станет квадратным уравнением:
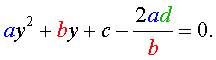 | (29) |
Найдем корни уравнения (29), а после этого, подставив каждый из найденных корней в равенство (28), решим полученное уравнение относительно x .
Описание метода решения уравнений вида (25) завершено.
Пример 4 . Решить уравнение
| 2x 4 – 15x 3 + 35x 2 – – 30 x + 8 = 0. | (30) |
Решение . Введем для коэффициентов уравнения (30) следующие обозначения
и найдем значение выражения
то уравнение (30) является обобщенным возвратным уравнением 4-ой степени. В соответствии с изложенным выше, разделим его на x 2 . В результате получится уравнение
Преобразуем левую часть уравнения (31):
В результате этого преобразования уравнение (31) принимает вид
Если теперь обозначить
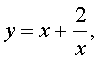 | (33) |
то уравнение (32) станет квадратным уравнением:
| 2y 2 – 15y + 27 = 0. | (34) |
В первом случае из равенства (33) получаем:
Во втором случае из равенства (33) получаем:
Ответ :
Видео:Как решить симметрическое уравнение | Сведение к квадратному | Замена переменнойСкачать

Чем отличаются возвратные уравнения от симметричных
Симметрическое уравнение нечетной степени имеет корень x = -1.
Симметрическое уравнение четной степени 2n с помощью подстановки $$ u = x + frac$$ сводится к уравнению степени n
Уравнения вида $$ a_0 x^ + a_1 x^ + . + a_n x^ + a_ x^n + . + a_ x + a_ = 0$$ называют возвратными уравнениями нечетной степени,
если $$frac <<a_>><> = lambda ^ ,quad frac <<a_>><> = lambda ^n ,quad frac <<a_>><> = lambda $$, где $$ lambda$$ — некоторое действительное число.
Возвратное уравнение нечетной степени имеет корень $$ x = — lambda $$.
Возвратное уравнение четной степени 2n с помощью подстановки $$ u = x + frac$$ сводится к уравнению степени n
Если обе части однородного уравнения разделить на $$ left( right)^n$$, применяя замену $$ t = frac<><>$$
получим уравнение $$ a_0 t^n + a_1 t^ + . + a_k t^ + . + a_n = 0$$
Видео:Симметрическое(возвратное) уравнение седьмой степени (ДВИ + ЕГЭ)Скачать

ТЕМА «СИММЕТРИЧЕСКИЕ И ВОЗВРАТНЫЕ УРАВНЕНИЯ»
элективный курс по алгебре (10 класс) по теме
Лекция 1. Симметрические уравнения третьей и четвертой степени.
Лекция 2. Возвратные уравнения.
Лекция 3. Уравнения четвертой степени с дополнительными условиями на коэффициенты.
Семинар 1. Решение симметрических и возвратных уравнений.
Практическая работа 1. Решение симметрических уравнений.
Практическая работа 2. Решение возвратных уравнений.
Самостоятельная работа. Решение симметрических и возвратных уравнений.
Видео:Рациональные уравнения №2. Возвратные уравнения 4-й степени. ЕГЭ математика профиль 2023. Задание 12Скачать

Скачать:
| Вложение | Размер |
|---|---|
| razrabotka_temy_elektivnogo_predmeta.rar | 8.9 КБ |
Видео:9 класс. Алгебра. Решение уравнений четвертой степени. Возвратные уравнения.Скачать

Предварительный просмотр:
ТЕМА «СИММЕТРИЧЕСКИЕ И ВОЗВРАТНЫЕ УРАВНЕНИЯ»
Учитель математики МБОУ СОШ № 34 г. Тихорецка Мирошниченко В.Н.
ТЕМА 3 «СИММЕТРИЧЕСКИЕ И ВОЗВРАТНЫЕ УРАВНЕНИЯ»
Лекция 1. Симметрические уравнения третьей и четвертой степени.
Лекция 2. Возвратные уравнения.
Лекция 3. Уравнения четвертой степени с дополнительными условиями на коэффициенты.
Семинар 1 . Решение симметрических и возвратных уравнений.
Практическая работа 1. Решение симметрических уравнений.
Практическая работа 2 . Решение возвратных уравнений.
Самостоятельная работа . Решение симметрических и возвратных уравнений.
Методическая разработка первого занятия по данной теме.
Цель изучения данной темы:
— расширить знания о видах уравнений;
— познакомить с методами их решения;
— учить решать трудные задачи.
Лекция 1. Симметрические уравнения третьей и четвертой степени.
ах 3 + вх 2 + вх + а = 0, а ≠ 0, (1)
называются симметрическими уравнениями третьей степени . Поскольку ах 3 + вх 2 + вх + а = а (х 3 + 1) + вх (х+1) = а (х+ 1) (х 2 — х+ 1) + вх (х+ 1) = (х+1) (ах 2 + (в — а) х + а), то уравнение (1) равносильно совокупности уравнений
х + 1 = 0 и ах 2 + (в — а) х + а = 0, решить которую просто.
Пример 1. Решить уравнение
3х 3 + 4х 2 + 4х + 3 = 0.
Уравнение является симметрическим уравнением третьей степени. Разложим на множители левую часть уравнения
3х 3 + 4х 2 + 4х + 3 = 3 (х 3 + 1) + 4х (х + 1) = ( х + 1) (3х 3 – 3х + 3 + 4х) = ( х+ 1) (3х 3 + х + 3).
Уравнение равносильно совокупности уравнений
х + 1 = 0 и 3х 3 + х + 3 = 0,
ах 4 + вх 3 + сх 2 + вх + а = 0 , а≠ 0,
называются симметрическими уравнениями четвертой степени.
Поскольку х = 0 не является корнем уравнения , то , разделив обе части уравнения на х 2 , получим уравнение . равносильное исходному:
ах 2 + а/х 2 + вх + в/х + с = 0.
Перепишем уравнение в виде:
а [(х + 1/х) 2 — 2 ] + в ( х + 1/х) + с = 0.
В этом уравнении сделаем замену х + 1/х = у. тогда получим квадратное уравнение
ау 2 + ву +с – 2а = 0.
Если уравнение имеет два корня у 1 и у 2 , то исходное уравнение равносильно совокупности уравнений
х 2 — х у 1 + 1 = 0 и х 2 — х у 2 + 1 = 0.
Если же уравнение имеет один корень у 0 , то исходное уравнение равносильно уравнению х 2 — у 0 х = 1 = 0.
Если уравнение не имеет корней, то и исходное уравнение не имеет корней.
Пример 2. Решить уравнение
х 4 – 5х 3 + 8х 2 – 5х- 1 =0.
Решение. Данное уравнение является симметрическим уравнением четвертой степени. Так как х= 0 не является его корнем, то , разделив уравнение на х 2 ,получим равносильное ему уравнение
х 2 – 5х + 8 – 5/х + 1/ х 2 = 0.
Сгруппировав слагаемые, перепишем уравнение в виде
(х 2 + 1/ х 2 ) 2 – 5 (х + 1/х) + 6 =0.
Пусть х + 1/х = у, получим уравнение
имеющее два корня у 1 = 2, у 2 = 3. Следовательно, исходное уравнение равносильно совокупности уравнений
х + 1/х =2 и х + 1/х =3.
Решение первого уравнения этой совокупности есть х 1 = 1, а решения второго есть х 2 =(3+√5)/2, х 3 =(3-√5)/2.
Следовательно, исходное уравнение имеет три корня.
Ответ: х 1 = 1, х 2 =(3+√5)/2, х 3 =(3-√5)/2.
- Домашнее задание: рассмотреть решение уравнений;
А) 7х 3 — 5х 2 — 5х + 7 = 0,
Б) 3х 3 + 4х 2 — 4х — 3 = 0,
С) 3х 4 – 4х 3 + 2х 2 – 4х + 3=0,
Д) х 4 +4х 3 — 2х 2 –+4х + 1=0.
Видео:симметричные и возвратные уравнения. Пример решения заданий ЕГЭ. математикаСкачать

По теме: методические разработки, презентации и конспекты
Занятие по теме «Решение простейших тригонометрических уравнений. Уравнение tgx=a»
Занятие проводилось в рамках программы ШТК по математике. Презентация выполнена в программе Смарт и демонстрируется на интерактивной доске.Архив содержит все необходимые материалы.
урок по теме «Примеры решения тригонометрических уравнений и систем уравнений»
Класс 10Урок закрепления.
Тема 15. ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 9-14: «Показательные уравнения. Показательно-степенные уравнения. Показательные неравенства. Преобразования и вычисления логарифмических выражений. Логарифмические уравнения. Логарифмические неравенства».
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступител.
урок по теме «Способы решения тригонометрических уравнений»(урок одного уравнения) 08.03.16
методическая разработка урока алгебры и начал математического анализа в 10 классе по УМК Мордкович, содержит спсобы решения тригонометрического уравнения вида asinx +bcosx=c.
Дидактический материал по темам: «Логарифмическая функция. Логарифмические уравнения, неравенства и системы», «Показательная функция. Показательные уравнения, системы и неравества»
Тренировочные задания по темам:«Показательная функция. Показательные уравнения, неравенства и системы»«Логарифмическая функция. Логарифмические уравнения, неравенства и системы»Данный дидак.
Презентации по теме «Системы двух линейных уравнений», «Метод подстановки для решения систем уравнений», «Метод сложения для решения систем уравнений» .
Презентации проедполагает использование при проведении онлайн урока по теме «Системы двух линейных уравнений», «Метод подстановки для решения систем уравнений», «Метод сложени.
Научная статья на тему: «Симметрические многочлены»
Научная статья на тему: «Симметрические многочлены".
💡 Видео
Возвратные уравненияСкачать

Симметричные системы #1Скачать

Возвратные уравнения 3 степениСкачать

Уравнение четвертой степениСкачать

Симметричные уравнения четвертой степени. Рациональные уравнения Часть 3 из 4Скачать

Возвратные уравнениями 4 й степениСкачать

Симметрические уравнения третьей и четвертой степениСкачать

САВВАТЕЕВ ДОМА + РЕШЕНИЕ ВОЗВРАТНОГО УРАВНЕНИЯ!Скачать

2.5. Дробно-рациональные уравнения. Симметричные, возвратные и другие уравнения.Скачать

Симметрические и возвратные уравненияСкачать

Можно ли решить уравнение 5-й степени? – математик Алексей Савватеев | НаучпопСкачать

Математика | Система уравнений на желтую звездочку (feat Золотой Медалист по бегу)Скачать