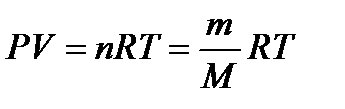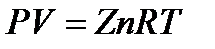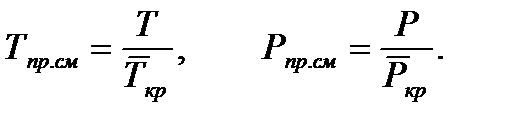Уравнение состояния идеальных газов.аналитическая зависимость между основными параметрами состояния газа (объем, давление и температура). Уравнением состояния идеальных газов называют уравнение Менделеева-Клапейрона или Клапейрона-Менделеева, 
где Р – абсолютное давление, Па; V – объем занимающий газом, м 3 ; n – число киломолей газа; m – масса вещества; М – молекулярная масса; Т – абсолютная температура, К; R – универсальная газовая постоянная, 8314,3 Дж/(кмоль∙К).
Универсальная газовая постоянная – это работа расширения одного моля газа при нагревании на один градус при постоянном давлении. В системе СИ измеряется Дж/(моль*К) и равняется 8,3143.
Уравнение состояния реальных газовДля описания поведения природных газов во время добычи, переработки и транспортировки, при давлениях выше атмосферного, наиболее широко в отрасли используется следующее уравнение:
где Z – безразмерный коэффициент сферхсжимаемости газа, который вводится в уравнение состояния идеального газа, для того чтобы учитывать отклонение реального газа от законов идеального.
7. Критические параметры газа: Ткр , Ркр .
Критическим состоянием вещества (газа) является такое состояние, при котором исчезает граница между его газовой и жидкой фазой и свойства этих фаз становятся равными друг другу.
Критические параметры газа.Критической называется такая температура, выше которой, при любом давлении, газ не может быть переведен в жидкое состояние. Давление, необходимое для сжижения газа при критической температуре, называется критическим.Приведенные параметры газа.Приведенными параметрами называют безразмерные величины, показывающие, во сколько раз действительные параметры состояния газа (давление, температура, плотность, удельный объем) больше или меньше критических: 
Дата добавления: 2016-12-27 ; просмотров: 5567 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать
Разница между идеальным и реальным газом
Исследователи выделяют модели газа идеального и реального. В чем их специфика?
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать
Что представляет собой идеальный газ?
В науке распространена трактовка понятия «идеальный газ», соответствующая гипотетическому веществу (не существующему в реальности), свойства которого могут быть описаны посредством уравнения Клапейрона — Менделеева.
Под идеальным газом понимается математическая модель соответствующего вещества, которая характеризуется:
- возможностью пренебрежения потенциальной энергией, образующейся в процессе взаимодействия частиц газа — в сравнении с уровнем кинетической энергии данных частиц;
- крайне малым общим объемом составляющих газ частиц;
- очень малым присутствием или же отсутствием дистанционных сил притяжения частиц либо отталкивания их;
- очень малым временем взаимодействия частиц друг с другом.
к содержанию ↑
Видео:Уравнение состояния идеального газа. 10 класс.Скачать
Что представляет собой реальный газ?
Под реальным газом, в свою очередь, понимается вещество, которое не может быть описано уравнением Клапейрона — Менделеева. Так, молекулы, присутствующие в нем, взаимодействуют друг с другом, формируют некоторый объем.
Нужно отметить, что во многих случаях характеристики потенциальной энергии, формирующейся в ходе взаимодействия молекул реального газа, существенно ниже кинетической энергии. Вследствие чего соответствующие газы по своим свойствам приближаются к тем, что характеризуют идеальный газ. Заметные различия между рассматриваемыми веществами начинают появляться, как правило, при повышении давления и снижении температуры.
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать
Сравнение
Главное отличие идеального газа от реального заключается в том, что в модели первого вещества практически не учитывается объем молекул, а также энергия их взаимодействия. В реальном газе соответствующие показатели учитываются. Вместе с тем при невысоком давлении и большой температуре реальный газ по своим свойствам близок к идеальному.
Определив, в чем разница между идеальным и реальным газом, зафиксируем выводы в таблице.
Видео:идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать
Уравнение состояния вещества
Параметры состояния связаны друг с другом. Соотношение, при котором определяется данная связь, называют уравнением состояния данного тела. В самом простом случае равновесное состояние тела определяется значением следующих параметров: давления p , объема V и температуры (масса тела или системы, как правило, известна).
Видео:Уравнение состояния идеального газаСкачать
Что такое идеальный газ
Уравнение состояния так называемого идеального газа является простым, но достаточно информативным.
Идеальный газ – это газ, в котором пренебрегают взаимодействием молекул между собой.
Идеальными считают разреженные газы. Особенно близки к идеальным газы гелий и водород. Идеальный газ – это упрощенная математическая модель реального газа: молекулы движутся хаотически, а соударения между молекулами и удары молекул о стенки сосуда упругие, не приводящие к потерям энергии в системе. Подобная упрощенная модель весьма удобна, поскольку не требует учета силы взаимодействия между молекулами газа. Множество реальных газов не отличаются в своем поведении от идеального газа в условиях, когда суммарный объем молекул пренебрежимо мал в сравнении с объемом сосуда (то есть при атмосферном давлении и комнатной температуре). Это дает возможность применять уравнение состояния идеального газа для сложных расчетов.
Уравнение состояния идеального газа запишем несколько раз ( 2 ) , ( 3 ) , ( 5 ) :
p V = m μ R T = ν R T ( 2 ) .
Уравнение ( 2 ) – уравнение Менделеева-Клапейрона, где m – это масса газа, μ – это молярная масса газа, R = 8 , 31 Д ж м о л ь · К – это универсальная газовая постоянная, ν – это число молей вещества.
где N – это количество молекул газа в массе m , k = 1 , 38 · 10 — 23 Д ж К , постоянная Больцмана, определяющая «долю» газовой постоянной, которая приходится на 1 молекулу и
N A = 6 , 02 · 10 23 м о л ь — 1 – это постоянная Авогадро.
Если поделить в ( 4 ) обе части на V , то получаем следующий вид записи уравнения состояния идеального газа:
где n = N V – это количество частиц в единице объема или же концентрация частиц.
Видео:Уравнение состояния идеального газаСкачать
Что такое реальный газ
Рассмотрим теперь более сложные системы: неидеальные газы и жидкости.
Реальный газ – это газ, между молекулами которого наблюдаются заметные силы взаимодействия.
Необходимо учитывать, что в неидеальных, плотных газах взаимодействие молекул высоко. Известно, что взаимодействие молекул очень сильно усложняет физическую картину, потому точную формулу уравнения состояния неидеального газа не получается записать в простом виде. В данном случае прибегают к приближенным формулам, найденным полу-эмпирическим путем. Самая удачная формула – это уравнение Ван-деp-Ваальса.
Взаимодействие молекул обладает сложным характером. На достаточно больших расстояниях между молекулами действуют силы притяжения. С уменьшением расстояния силы притяжения вначале растут, однако потом уменьшаются и преобразуются в силы отталкивания. Притяжение и отталкивание молекул будем рассматривать и учитывать отдельно. Уравнение Ван-дер-Ваальса, которое описывает состояние одного моля реального газа, имеет вид:
p + a V μ 2 V μ — b = R T ( 6 ) ,
где a V μ 2 – это внутреннее давление, обусловленное силами притяжения между молекулами, b – это поправка на собственный объем молекул, учитывающая действие сил отталкивания между молекулами, при этом:
b = N A 2 3 πd 3 ( 7 ) ,
где d – это диаметр молекулы. Значение a рассчитывается по формуле:
a = — 2 πN A 2 ∫ d ∞ W p ( r ) r 2 dr ( 8 ) ,
где W p ( r ) – это потенциальная энергия притяжения 2 -х молекул.
При увеличении объема значение поправок в уравнении ( 6 ) становится менее существенным. И в пределе уравнение ( 6 ) превращается в уравнение ( 2 ) . Это согласовано с тем фактом, что с уменьшением плотности реальные газы по своим характеристикам приближаются к идеальным.
Положительным в уравнении Ван-деp-Ваальса является тот факт, что данное равенство при очень больших плотностях приблизительно описывает также и свойства жидкости, в частности, плохую ее сжимаемость. Потому существует основание предполагать, что уравнение Ван-деp-Ваальса позволяет отразить и переход от жидкости к газу (либо от газа к жидкости).
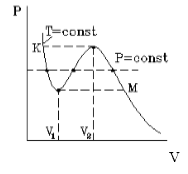
На рисунке 1 представлена изотерма Ван-дер-Ваальса для некоторого постоянного значения температуры T , которая построена из соответствующего уравнения.
В месте “извилины” (участок КМ) изотерма 3 раза пересекает изобару. На участке
V 1 , V 2 давление увеличивается с ростом объема.
Подобная зависимость невозможна. Это означает, что в этой области с веществом происходит что-то необыкновенное. Что именно, не видно в уравнении Ван-деp-Ваальса. Обратимся к опыту. В месте “извилины” на изотерме в состоянии равновесия вещество расслаивается на 2 фазы: жидкую и газообразную. Обе фазы существуют одновременно и находятся в фазовом равновесии. В таком состоянии происходит испарение жидкости и конденсация газа. Процессы протекают с такой интенсивностью, что полностью компенсируют друг друга: объем жидкости и газа со временем не изменяется.
Газ, который находится в фазовом равновесии со своей жидкостью, называется насыщенным паром. Если фазовое равновесие отсутствует, отсутствует также компенсация испарения и конденсации, тогда газ называется ненасыщенным паром.
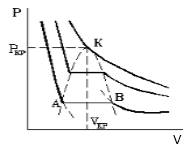
Что происходит с изотермой в области двухфазного состояния вещества (то есть в месте «извилины» изотермы Ван-деp-Ваальса)? Эксперимент показывает, что в этом месте при изменении объема давление остается неизменным. График изотермы идет параллельно оси V (рисунок 2 ).
С увеличением температуры участок двухфазных состояний на изотермах уменьшается до тех пор, пока не превращается в точку (рисунок 2 ). Это особая точка К , в которой исчезает разница между жидкостью и паром. Ее называют критической точкой.
Параметры, которые соответствуют критическому состоянию, являются критическими (критическая температура, критическое давление, критическая плотность вещества).
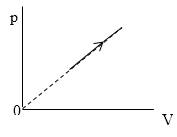
Необходимо найти величину n . В процессе, представленном на рисунке 3 , давление p
Из графика, приведенного на рисунке 3 , запишем уравнение процесса в параметрах p ( V ) :
С учетом уравнения Менделеева-Клайперона:
V вместо объема, получаем:
Моль кислорода охлаждают до — 100 ° C . Необходимо определить давление, которое оказывает газ на стенки сосуда, если занимаемый газом объем V = 0 , 1 л . Необходимо также сравнить p с давлением идеального газа p i d , если бы кислород вел себя как идеальный газ. Величина постоянных Ван-дер-Ваальса a и b , для кислорода a = 0 , 1358 П а · м 6 / м о л ь 2 , b = 3 , 167 · 10 — 5 м 3 / м о л ь .
Из уравнения Ван-Дер-Ваальса имеем:
p = R T V μ — b — a V μ 2
Переведем температуру в систему измерения: T = t + 273 , По условию T = 173 K , V = 0 , 1 л = 10 — 4 м 3 .
Произведем расчет: p = 8 , 31 · 173 ( 10 — 3 , 2 ) · 10 — 5 — 0 , 1358 ( 10 — 4 ) 2 = 75 , 61 · 10 5 ( П а ) .
Для идеального газа:
Рассчитаем: p i d = 1 · 8 , 31 · 173 10 — 4 = 143 · 10 5 ( П а ) .
🔥 Видео
Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать
Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать
Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать
Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать
Урок 194. Уравнение Ван-дер-ВаальсаСкачать
Реальный газ Уравнение Ван-Дер-ВаальсаСкачать
ЕГЭ. Физика. Уравнение состояния идеального газа. ПрактикаСкачать
Урок 90. Уравнение состояния термодинамической системы. Уравнение состояния газа.Скачать
ЕГЭ по физике. Теория #25. Идеальный газ. Уравнение состояния идеального газаСкачать
Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать
Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать
