Интегра́льное уравне́ние — функциональное уравнение, содержащее интегральное преобразование над неизвестной функцией. Если интегральное уравнение содержит также производные от неизвестной функции, то говорят об интегро-дифференциальном уравнении.
- Классификация интегральных уравнений
- Линейные интегральные уравнения
- Уравнения Фредгольма
- Уравнения Вольтерра
- Нелинейные уравнения
- Уравнения Урысона
- Уравнения Гаммерштейна
- Уравнения Ляпунова — Лихтенштейна
- Нелинейное уравнение Вольтерра
- Методы решения
- Преобразование Лапласа
- Метод последовательных приближений
- Метод резольвент
- Метод сведения к алгебраическому уравнению
- Приложения
- Формула обращения Фурье
- Сведение задачи Коши к интегральному уравнению
- Задача Абеля
- ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА И ВОЛЬТЕРРА КАК АППАРАТ ЗАДАЧ ЭКОНОМИЧЕСКОЙ ДИНАМИКИ, ИХ СХОДСТВО И РАЗЛИЧИЕ Текст научной статьи по специальности « Математика»
- Аннотация научной статьи по математике, автор научной работы — Паршикова Г.Ю., Силаев А.А., Тарарин И.М.
- Похожие темы научных работ по математике , автор научной работы — Паршикова Г.Ю., Силаев А.А., Тарарин И.М.
- FREDHOLM AND VOLTERRA INTEGRAL EQUATIONS AS A MATHEMATICAL APPARATUS FOR PROBLEMS OF ECONOMIC DYNAMICS, THEIR SIMILARITIES AND DIFFERENCES
- Текст научной работы на тему «ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА И ВОЛЬТЕРРА КАК АППАРАТ ЗАДАЧ ЭКОНОМИЧЕСКОЙ ДИНАМИКИ, ИХ СХОДСТВО И РАЗЛИЧИЕ»
- Содержание
- Введение.
- Глава I. Общие сведения об интегральных уравнениях.
- Глава II. Вычисление определенных интегралов на Mathcad
- 2.1. Метод Ромберга
- 2.2. Использование пакетов MathCAD для решения дифференциальных уравнений.
- 2.3. Метод Эйлера для дифференциальных уравнений первого порядка
- 2.4. Решение дифференциальных уравнений второго порядка
- Глава III Численные методы решения интегральных уравнений.
- 3.1. Квадратурный метод решения интегральных уравнений Фредгольма.
- 3.2. Квадратурный метод решения интегральных уравнений Вольтерры.
- Глава IV. Прикладные задачи, использующие решение интегральных уравнений.
- 4.1. Расчет теплоизоляции.
- Листинг№1 Численное интегрирование
- 1. Функция, возвращающая значение интеграла функции помощью метода Симпсона
Видео:Интегральные уравнения ВольтерраСкачать

Классификация интегральных уравнений
Линейные интегральные уравнения
Это интегральные уравнения, в которые неизвестная функция входит линейно:
где 


Уравнения Фредгольма
Уравнения Фредгольма 2-го рода
Уравнения Фредгольма 2-го рода — это уравнения вида:
Пределы интегрирования могут быть как конечными, так и бесконечными. Переменные удовлетворяют неравенству: 

Ядра, удовлетворяющие последнему условию, называют фредгольмовыми. Если 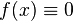
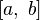
Уравнения Фредгольма 1-го рода
Уравнения Фредгольма 1-го рода выглядят также, как и уравнение Фредгольма 2-го рода, только в них отсутствует часть, содержащая неизвестную функцию вне интеграла:
при этом ядро и свободный член удовлетворяют условиям, сформулированным для уравнений Фредгольма 2-го рода.
Уравнения Вольтерра
Уравнения Вольтерра 2-го рода
Уравнения Вольтерра отличаются от уравнений Фредгольма тем, что один из пределов интегрирования в них является переменным:
Уравнения Вольтерра 1-го рода
Также, как и для уравнений Фредгольма, в уравнениях Вольтерра 1-го рода отсутствует неизвестная функция вне интеграла:
В принципе, уравнения Вольтерра можно рассматривать как частный случай уравнений Фредгольма, если переопределить ядро:
Однако некоторые свойства уравнений Вольтерра не могут быть применены к уравнениям Фредгольма.
Нелинейные уравнения
Можно придумать немыслимое многообразие нелинейных уравнений, поэтому дать им полную классификацию не представляется возможным. Вот лишь их некоторые типы, имеющие большое теоретическое и прикладное значение.
Уравнения Урысона
Постоянная M — это некоторое положительное число, которое заранее не всегда может быть определено.
Уравнения Гаммерштейна
Уравнения Гаммерштейна являются важным частным случаем уравнения Урысона:
где 
Уравнения Ляпунова — Лихтенштейна
Именами Ляпунова — Лихтенштейна принято называть уравнения, содержащие существенно нелинейные операторы, например, уравнение вида:
Нелинейное уравнение Вольтерра
где функция 
Видео:Метод определителей ФредгольмаСкачать

Методы решения
Прежде, чем рассмотреть некоторые методы решения интегральных уравнений, следует заметить, что для них, как и для дифференциальных уравнений не всегда удается получить точное аналитическое решение. Выбор метода решения зависит от вида уравнения. Здесь будут рассмотрены несколько методов для решения линейных интегральных уравнений.
Преобразование Лапласа
Метод преобразования Лапласа может быть применён к интегральному уравнению, если входящий в него интеграл имеет вид свёртки двух функций:
то есть, когда ядро является функцией разности двух переменных:
Например, дано такое уравнение:
Применим преобразование Лапласа к обеим частям уравнения:

Применяя обратное преобразование Лапласа, получим:
Метод последовательных приближений
Метод последовательных приближений применяется для уравнений Фредгольма 2-го рода, если выполняется условие:
Это условие необходимо для сходимости ряда Лиувилля — Неймана:
который и является решением уравнения. (K k f)(x) — k -ая степень интегрального оператора (Kf)(x) :
Впрочем, такое решение является хорошим приближением лишь при достаточно малых | λ | .
Метод резольвент
Метод резольвент является не самым быстрым решением интегрального уравнения Фредгольма второго рода, однако иногда нельзя указать других путей решения задачи.
Если ввести следующие обозначения:
то повторными ядрами ядра 
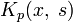
Ряд, составленный из повторных ядер,
называется резольвентой ядра 


Например, для интегрального уравнения
повторными будут следующие ядра:
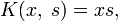
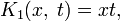

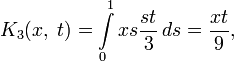
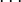
а резольвентой — функция
Тогда решение уравнения находится по формуле:
Метод сведения к алгебраическому уравнению
В случае, если ядро интегрального уравнения Фредгольма является вырожденным, то есть 
где 
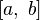
где 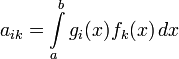

Видео:Методы численного анализа - Уравнения Фредгольма и ВольтерраСкачать

Приложения
Термин «интегральное уравнение» ввёл в 1888 году Дюбуа-Реймон, однако первые задачи с интегральными уравнениями решались и ранее. Например, в 1811 году Фурье решил задачу об обращении интеграла, которая теперь носит его имя.
Формула обращения Фурье
Задача состоит в нахождении неизвестной функции f(y) по известной функции g(x) :
Фурье получил выражение для функции f(y) :
Сведение задачи Коши к интегральному уравнению
К нелинейным интегральным уравнениям Вольтерра приводит задача Коши для обыкновенных дифференциальных уравнений:
В самом деле, это уравнение можно проинтегрировать по t от a до t :
Решение начальной задачи для линейных дифференциальных уравнений приводит к линейным интегральным уравнениям Вольтерра 2-го рода. Этим еще в 1837 году воспользовался Лиувилль. Пусть, например, поставлена задача:
Для уравнения с постоянными коэффициентами с теми же начальными условиями:
решение может быть найдено методом вариации постоянных и представлено в виде:
Тогда для исходного уравнения получается:
— интегральное уравнение Вольтерра 2-го рода.
a,» src=»http://upload.wikimedia.org/math/3/c/c/3cca9038417f8968682c783191e3f6c7.png» />
также может быть сведено к интегральному уравнению Вольтерра 2-го рода.
Задача Абеля
Исторически считается, что первой задачей, которая привела к необходимости рассмотрения интегральных уравнений, является задача Абеля. В 1823 году Абель, занимаясь обобщением задачи о таутохроне, пришёл к уравнению:
где f(x) — заданная функция, а 
У Абеля формулировка задачи выглядела примерно так:
Материальная точка под действием силы тяжести движется в вертикальной плоскости
по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.
Если обозначить угол между касательной к траектории и осью Oξ как β и применить законы Ньютона, можно прийти к следующему уравнению:
Видео:Как проверяют учеников перед ЕНТСкачать

ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА И ВОЛЬТЕРРА КАК АППАРАТ ЗАДАЧ ЭКОНОМИЧЕСКОЙ ДИНАМИКИ, ИХ СХОДСТВО И РАЗЛИЧИЕ Текст научной статьи по специальности « Математика»
Видео:Уравнения Фредгольма - 1Скачать

Аннотация научной статьи по математике, автор научной работы — Паршикова Г.Ю., Силаев А.А., Тарарин И.М.
В статье авторы обосновывают утверждение, что интегральное уравнение Вольтерра не является частным случаем интегрального уравнения Фредгольма: переход к расширенному ядру делает его разрывным и, следовательно, большинство теорем Фредгольма не переносится на уравнения Вольтерра. Авторы исследуют важный частный случай, при котором ядро уравнения является вырожденным и разбирают оригинальный подход, состоящий в построении асимптотического решения уравнения Вольтерра. Кроме того, построена ортогональная система по отношению к ядру, с точностью до постоянных множителей совпадающему с плотностью нормального распределения вероятностей. В заключении работы отмечаются направления, по которым следует разрабатывать аспекты, связанные с применением интегральных уравнений Фредгольма и Вольтерра в задачах экономической динамики — это прежде всего для математического моделирования возникающих финансовых задач и проблем финансового рынка. Особенно адекватным аппарат интегральных уравнений становится во времена социально-экономической нестабильности.
Видео:Уравнения Вольтерра - 1Скачать

Похожие темы научных работ по математике , автор научной работы — Паршикова Г.Ю., Силаев А.А., Тарарин И.М.
Видео:Интегральные уравнения Вольтерра второго рода Метод последовательных приближенийСкачать

FREDHOLM AND VOLTERRA INTEGRAL EQUATIONS AS A MATHEMATICAL APPARATUS FOR PROBLEMS OF ECONOMIC DYNAMICS, THEIR SIMILARITIES AND DIFFERENCES
In the article, the authors substantiate the statement that the Volterra integral equation is not a special case of the Fredholm integral equation: the transition to the extended kernel makes it discontinuous and, consequently, most of the Fredholm theorems are not transferred to the Volterra equations. The authors investigate an important special case in which the kernel of the equation is degenerate and analyze the original approach, which consists in constructing an asymptotic solution to the Volterra equation. In addition, an orthogonal system is constructed with respect to the kernel, which coincides with the density of the normal probability distribution up to constant factors. In conclusion, the paper notes the directions in which it is necessary to develop aspects related to the application of the integral Fredholm and Volterra equations in problems of economic dynamics — this is primarily for mathematical modeling of emerging financial problems and financial market problems. The apparatus of integral equations becomes especially adequate in times of socio-economic instability.
Видео:Интегральные уравнения с вырожденным ядромСкачать

Текст научной работы на тему «ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ФРЕДГОЛЬМА И ВОЛЬТЕРРА КАК АППАРАТ ЗАДАЧ ЭКОНОМИЧЕСКОЙ ДИНАМИКИ, ИХ СХОДСТВО И РАЗЛИЧИЕ»
Интегральные уравнения Фредгольма и Вольтерра как аппарат задач экономической динамики, их сходство и различие
Не можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
Видео:УРАВНЕНИЕ ОКРУЖНОСТИ 8 и 9 класс геометрияСкачать

Содержание
Глава I. Общие сведения об интегральных уравнениях. 7
Глава II. Вычисление определенных интегралов на Mathcad. 11
2.1. Метод Ромберга. 11
2.2. Использование пакетов MathCAD для решения дифференциальных уравнений. 14
2.3. Метод Эйлера для дифференциальных уравнений первого порядка 16
2.4. Решение дифференциальных уравнений второго порядка. 17
Глава III Численные методы решения интегральных уравнений. 20
3.1. Квадратурный метод решения интегральных уравнений Фредгольма. 24
3.2. Квадратурный метод решения интегральных уравнений Вольтерры. 27
Глава IV. Прикладные задачи, использующие решение интегральных уравнений. 29
4.1. Расчет теплоизоляции. 29
4.2. Фильтр Калмана. 33
Листинг№1 Численное интегрирование. 39
1. Функция, возвращающая значение интеграла функции помощью метода Симпсона 39
2. Функция, возвращающая значение интеграла с помощью формулы трапеции 39
3. Функция, возвращающая значение интеграла, найденного по формулам треугольников. 40
Листинг № 2 Решение обыкновенных дифференциальных уравнений. 41
1.Функция, возвращающая численное решение ДУ методом Адамса. 41
2. Задание функции возвращающей решение ДУ методом Пикара. 42
3.Метод Эйлера. 42
Листинг №3. Решение линейного интегрального уравнения Вольтерра I-го рода. 43
Листинг №4. Решение линейного интегрального уравнения Вольтера II-го рода. 44
Листинг №6. Фильтр Калмана. 45
Список литературы: 50
Видео:Уравнение годаСкачать

Введение.
Интегральные уравнения являются одними из наиболее плодотворных средств математического исследования, как в чистом, так и в прикладном анализе. Это относится, в частности, к задачам теории механических колебаний и соответствующих областей техники и теоретической физики, где интегральные уравнения не только полезны, но зачастую даже совершенно необходимы для численных расчетов.
Интегральным уравнением называется уравнение относительно неизвестно функции, содержащейся под знаком интеграла.
К интегральным уравнениям приводят многие задачи, возникающие в математике и математической физике. Исторически, первой задачей, сведенной к интегральному уравнению
cчитается задача Абеля, имеющая следующую формулировку:
Определить вид кривой 




Интегральные уравнения широко используются в моделях, рассматриваемых в теории упругости, газовой динамики, электродинамике, экологии и других областях физики, в которых они являются следствием законов сохранения массы, импульса и энергии. Достоинство данных моделей состоит в том, что интегральные уравнения, в отличие от дифференциальных, не содержат производных искомой функции и, следовательно. Жесткие ограничения на гладкость решения отсутствует.
В данной работе я постаралась отобразить основные возможности применения интегральных уравнений в различных областях жизни, а так же их численное решение с помощью средств компьютерной математики.
Целью данной работы является рассмотрение решения интегральных уравнений с помощью систем компьютерной математики, решение задачи Коши, а так же их практическое применение в задачах физики и механики.
В данной теме важным оказывается выбор базового программного средства.
Пакет Mathematica является сегодня наиболее популярным среди ученых, особенно теоретиков. Пакет предоставляет широкие возможности в проведении символических (аналитических) преобразований, однако требует значительных ресурсов компьютера.
Пакет Maple также весьма популярен. Кроме аналитических преобразований, пакет в состоянии решать задачи численно. Характерной особенностью пакета является то, что он позволяет конвертировать документы в формат LaTeX — стандартный формат подавляющего большинства научных издательств мирового класса. Кроме того, ряд других программных продуктов используют интегрированный символьный процессор Maple. Например, пакет подготовки научных публикаций Scientific WorkPlace позволяет обращаться к символьному процессору Maple, производить аналитические преобразования и встраивать полученные результаты в создаваемый документ[1].
Пакет Matlab фактически представляет собой своеобразный язык программирования высокого уровня, ориентированный на решение научных задач. Характерной особенностью пакета является то, что он позволяет сохранять документы в формате языка программирования С.
Пакет Mathcad более популярен в инженерной, чем в научной, среде. Характерной особенностью является использование привычных стандартных математических обозначений, т. е. вид документа на экране максимально приближен к общепринятой математической нотации.
В отличие от упомянутых выше пакетов, Mathcad является средой визуального программирования, т. е. не требует знаний специфического набора команд. Простота освоения пакета, дружественный интерфейс, относительная непритязательность к возможностям компьютера явились главными причинами того, что именно этот пакет был выбран мной для реализации численного решения интегральных уравнений.
Видео:Курс по ИДУ: Методы решения интегральных уравнений Вольтерра и Фредгольма | Занятие 6Скачать

Глава I. Общие сведения об интегральных уравнениях.
Интегральными уравнениями называются функциональные уравнения, содержащие интегральные преобразования над неизвестной функцией 


где 



Линейное интегральное уравнение первого рода получается при 

Однородное линейное интегральное уравнение второго рода получается при 
Неоднородное интегральное уравнение второго рода получается при g(x) = 1 и имеет вид
Уравнения вида 
Линейное интегральное уравнение Вольтерра первого рода имеет вид:
Если 





Представленная процедура решает уравнение методом квадратурных формул. Вычисление интеграла производится по формуле трапеций с постоянным шагом h:

где
Aj = 1 при j > 1 и Aj = 0.5 при j = 1
Линейное интегральное уравнение Вольтера второго рода имеет вид:
Причем независимые переменные 





Уравнение данного типа решается с помощью метода квадратурных формул, суть которого состоит в замене интегрального уравнения аппроксимирующей системой алгебраических уравнений относительно дискретных значений искомой функции и решении этой системы. В основе такой замены лежит приближение интеграла квадратурными формулами. Применение формулы трапеций с постоянным шагом h приводит к рекуррентной формуле:
· Aj = 1 при j > 1 и Aj = 0.5 при j = 1.
Линейное интегральное неоднородное уравнение Фредгольма второго рода имеет вид:
где ядро определено в квадрате 

· Aj = 1 при j, не равном 1 или n
· Aj = 0.5 при j, равном 1 или n.
Получаем систему линейных уравнений, которую решаем методом Гаусса с частичным выбором ведущего элемента. При решении полученной системы уравнений возможны два случая — система вырождена и нам придется поделить на ноль в ходе решения, или система невырождена. Если система невырождена, то существует одно и только одно решение. Если же система вырождена, то данный алгоритм неприменим. В случае вырожденой матрицы функция возвращает False. Если матрица невырождена, то функция возвращает True, а переменная Y содержит решение системы.
Для сравнения с нолем в алгоритм передается малое число epsilon, и любое число, по модулю меньшее epsilon, считается нолем.
Видео:Простейшие интегральные уравненияСкачать

Глава II. Вычисление определенных интегралов на Mathcad
Видео:Решить интегральное уравнениеСкачать

2.1. Метод Ромберга
Пусть требуется вычислить определенный интеграл на интервале [a;b].
Далеко не всегда задача может быть решена аналитически. В частности, численное решение требуется в том случае, когда подынтегральная функция задана таблично. Для численного интегрирования подынтегральную функцию аппроксимируют какой-либо более простой функцией, интеграл от которой может быть вычислен. Обычно в качестве аппроксимирующей функции используют полином. В случае полинома нулевой степени метод численного интегрирования называют методом прямоугольников, в случае полинома первой степени – методом трапеций, в случае полинома второй степени – методом Симпсона. Все эти методы являются частными случаями квадратурных формул Ньютона-Котеса.
Итак, в методе трапеций подынтегральную функцию аппроксимируют полиномом первой степени, то есть прямой линией. Это значит, что вместо площади криволинейной трапеции мы будем искать площадь прямоугольной трапеции. Приближенное значение интеграла равно
Погрешность этой формулы равна 
Обозначим 

Оценку значения интеграла можно сделать более точной, если разбить интервал на n частей и применить формулу трапеций для каждого такого интервала
Если разбить интервал на две части, то есть уменьшит шаг в два раза 
В данном случае суммирование включает только один элемент. Обратите внимание, в новую оценку вошла старая оценка. Нам потребовалось определять значение функции только в новых узлах[3].
Если имеется 2n подинтервалов, то
Вообще, справедливо рекуррентное соотношение
Полученное соотношение называют рекурсивной формулой трапеций и часто применяют для вычисления определенных интегралов. Преимущество этой формулы состоит в том, что при увеличении числа подинтервалов функцию нужно вычислять только во вновь добавленных точках. К сожалению, с помощью этой формулы нельзя получить сколь угодно точное значение интеграла. Во-первых, при увеличении числа разбиений объем вычислений стремительно возрастает; во-вторых, на каждом шаге накапливается ошибка округлений. Для дальнейшего уточнения значения интеграла можно сделать следующий шаг – экстраполировать полученную последовательность значений на случай бесконечного числа точек или что то же самое, на случай нулевого шага. Такой подход называется методом Ромберга.
Метод Ромберга заключается в том, что полученные оценки значения интеграла экстраполируют на случай бесконечного числа разбиений (величины шага равной нулю) по рекуррентной формуле

То есть строится следующий треугольник
R(5,1) R(5,2) R(5,3) R(5,4) R(5,5) ,
в котором первый столбец состоит из значений интеграла, полученных при последовательном удвоении числа интервалов. Второй столбец – результат уточнения значений первого столбца по рекуррентной формуле (1). Третий столбец – уточненные значения интеграла на основе второго столбца и т. д[4].
Формула (1) может быть получена различными способами. Можно, например, воспользоваться методом Невиля. Пусть имеется набор точек 



В нашем случае 




Видео:Интегральное уравнение Вольтерра второго рода Пример решения методом разрешающего ядраСкачать

2.2. Использование пакетов MathCAD для решения дифференциальных уравнений.
Пусть необходимо найти решение уравнения

с начальным условием 






Такой метод решения обыкновенных дифференциальных уравнений называется методом Эйлера. Геометрически метод Эйлера означает, что на каждом шаге мы аппроксимируем решение (интегральную кривую) отрезком касательной, проведенной к графику решения в начале интервала. Точность метода невелика и имеет порядок h. Говорят, что метод Эйлера – метод первого порядка, то есть его точность растет линейно с уменьшением шага h.
Существуют различные модификации метода Эйлера, позволяющие увеличить его точность. Все они основаны на том, что производную, вычисленную в начале интервала, заменяют на среднее значение производной на данном интервале[5]. Среднее значение производной можно получить (конечно же, только приближенно) различными способами. Можно, например, оценить значение производной в середине интервала 
Можно также оценить среднее значение производной на интервале
Такие модификации метода Эйлера имеет уже точность второго порядка.
Оценку значения производной можно улучшить, увеличивая число вспомогательных шагов. На практике наиболее распространенным методом решения обыкновенных дифференциальных уравнений является метод Рунге-Кутты четвертого порядка. Для оценки значения производной в этом методе используется четыре вспомогательных шага. Формулы метода Рунге-Кутты следующие
Перечисленные методы можно применять и для решения систем дифференциальных уравнений. Поскольку многие дифференциальные уравнения высших порядков могут быть сведены заменой переменных к системе дифференциальных уравнений первого порядка, рассмотренные методы могут быть использованы и для решения дифференциальных уравнений порядка выше первого.
Еще один тип задач, часто встречающихся на практике, – краевые задачи. Пусть имеется дифференциальное уравнение второго порядка 








Видео:Интегральные уравнения Фредгольма второго рода Случай вырожденного ядра Неоднородный случайСкачать
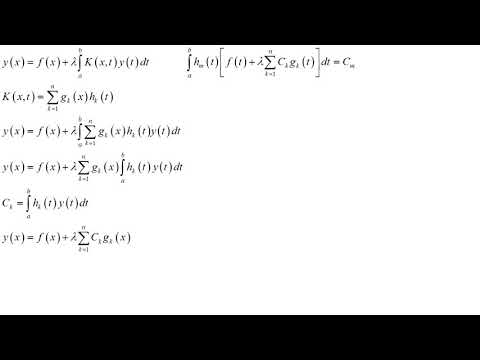
2.3. Метод Эйлера для дифференциальных уравнений первого порядка
Решим задачу Коши для дифференциального уравнения первого порядка 
Пусть правая часть уравнения равна
Зададим границы изменения x:
Зададим число точек и величину шага:
Зададим начальные условия:
Вычислим x и y по формулам Эйлера
Представим результат графически и сравним его с аналитическим решением
Точное аналитическое решение и решение, полученное численно, отличаются в точке x=1 на
То есть относительная ошибка составляет
Видео:Уравнения Фредгольма - 2Скачать

2.4. Решение дифференциальных уравнений второго порядка
В качестве примера решим задачу о гармоническом осцилляторе, для которого известно аналитическое решение, и легко может быть оценена точность вычислений. Дифференциальное уравнение второго порядка
преобразуем к системе из двух дифференциальных уравнений первого порядка
Пусть декремент затухания
Пусть циклическая частота
Зададим начальные условия
y0 соответствует начальной координате, а 

Представим результаты расчета на графике и сравним их с аналитическим решением
Для контроля точности вычислений нарисуем фазовую траекторию (зависимость смещения от скорости). Для гармонического осциллятора фазовая траектория должна иметь вид эллипса.
Примечание: Mathcad имеет еще две функции для решения задачи Коши. Это функции Rkadapt и Bulstoer. Эти функции имеют те же самые аргументы и возвращают решения в такой же форме, что и функция rkfixed. Первая из этих функций использует метод Рунге–Кутты с переменным шагом, что позволяет повысить точность вычислений и сократить их объем, если искомое решение имеет области, где ее значения меняются быстро, и области плавного изменения. Функция Rkadapt будет варьировать величину шага в зависимости от скорости изменения решения[7].
Функция Bulstoer реализует иной численный метод – метод Булирша–Штёра. Ее следует применять, если известно, что решение является гладкой функцией.
Видео:Курс по ИДУ: Интегральные уравнения Фредгольма с вырожденным ядром | Занятие 7Скачать

Глава III Численные методы решения интегральных уравнений.
Интегральное уравнение в достаточно общем виде можно записать в следующей форме:

где D — некоторая область n-мерного пространства;
x — неизвестная функция, зависящая от времени;
K — функция относительно x(линейная или нелинейная).
Далее мы ограничим рассмотрение одномерным линейными интегральными уравнениями, в которой функция x(t) является функцией, зависящей от одной переменной, а область D – отрезком конечной длины, в каждой точке которого подъинтегральная функция K(t, s,x(s)) представима в виде Q(t, s)x(s).
Классификация типов линейных интегральных уравнений приводится по виду верхней границы интеграла в 


где f(t) – неизвестная функция;
x(t)- решение уравнения;
Q(t, s)- ядро интегрального уравнения.
Ядро интегрального уравнения Фредгольма определяется на множестве точек квадрата [a, b]x[a, b],уравнения Вольтерры – в треугольнике 
Отметим, что доопределив ядро Q(t, s) уравнения Вольтерры нулем, в треугольнике 
Дополнительный множитель 


Значительно более сложной задачей оказывается задача доказательства существования, единственности и непрерывной зависимости решений от функции 


относящиеся к классу некорректных задач.
Уравнения первого и второго рода можно записать в общем виде, используя функцию h(t), тождественно равную нулю для уравнений первого рода и единице — для уравнений второго рода:

Когда функция h(t) обращается в ноль в некоторых точках прямоугольника интегрирования, уравнение 
Многие используемые на практике интегральные уравнения имеют ядро, зависящее только от разности t-s. Интегральные уравнения с данным типом ядра называются уравнениями с разностным ядром. Примером данного типа является уравнение, полученное в задаче Абеля[10].
Если Q(t, s) и f(t) – непрерывные функции, то при любых значениях параметра 
При снижении требований к гладкости возможных решений условие 
Известны формулы (или совокупность формул), позволяющие найти точное решение x(t). Например, решение уравнения Вольтерры, с 
вычисляется по формуле :
Решение уравнения Фредгольма с вырожденным ядром

где числа 



Условие существования и единственности решения уравнения Фредгольма с вырожденным ядром, очевидно. Зависит от значения определителя D(

Наличие методов нахождения точного решения интегрального уравнения с вырожденным ядром позволяет построить приближенный метод, в основе которого лежит замена одного уравнения другим, ядро которого вырождено и в некотором смысле близко к ядру исходного уравнения. Данная замена ядра опирается на различные способы локальной аппроксимации функций, зависящих от двух переменных. Помимо упомянутого выше метода замены ядра на вырожденно, известен ряд других приближенно-аналитических методов решения интегральных уравнений, например, метод последовательных приближений, метод моментов и другие.
Далее мы рассмотрим численные методы решения интегральных уравнений, в основе которого лежит замена интеграла в интегральном уравнении конечной суммой, используя какую-либо квадратурную формулу. Это позволяет свести решение исходной задачи к решению системы линейных алгебраических уравнений, число которых определяется числом узлов временной сетки. Методы решения интегральных уравнений, основанные на данном подходе, называются квадратурными методами или методами конечных сумм.
Преимущество данных методов состоит в простоте их реализации. Отметим, что без каких-либо изменений данные методы можно применять для решения нелинейных интегральных уравнений, имея в виду, что в этом случае приходится решать систему нелинейных алгебраических уравнений.
3.1. Квадратурный метод решения интегральных уравнений Фредгольма.
Заменим определенный интеграл

его приближенным значением, вычисляемым с помощью квадратурной формулы:

где j=1,2,…,n – номера узлов временной сетки; 
Подставив правую часть приближенного равенства с 
Данное выражение задает функцию, описывающую приближенное решение интегрального уравнения

Введем на отрезке [a, b] дискретную временную сетку 



И запишем равенство в виде системы n — линейных алгебраических уравнений с n неизвестными:
для решения, которой можно использовать любой из методов решения систем линейных алгебраических уравнений.
Таким образом, нахождение решения уравнения Фредгольма второго рода осуществляется в соответствии со следующим алгоритмом.
1. Задать временную сетку
2. Вычислить значение функции f(x) в узлах временной сетки.
3. Вычислить элементы матрицы, составленной из коэффициентов системы линейных алгебраических уравнений.
4. Решить систему линейных уравнений.
Точность численного решения интегрального уравнения зависит от нескольких факторов: применяемой квадратурной формулы, числа узлов временной сетки, свойств функции Q(t, s). В ряде книг приводятся аналитические выражения, позволяющие оценить максимальную погрешность численного решения при использовании различных вычислительных схем. Однако эти оценки оказываются малопригодными из-за их громоздкости, поэтому на практике используют менее строгий метод контроля точности численного решения — принцип Рунге.
Данный принцип состоит в сравнении численных решений, полученных на временных сетках с шагом 2h и h, в одних и тех же узлах временной сетки. Абсолютное значение разности данных решений характеризует величину погрешности численного решения. Недостаток данного подхода состоит в том, что при данном способе контроля приходится ограничиваться квадратурными формулами, пригодными только для сеток с равномерным шагом[11].
Важно понимать, что необходимо согласовывать выбор конкретной квадратурной формулы (точнее порядок ее точности) со степенью гладкости ядра интегрального уравнения. Если ядро и свободный член оказываются недостаточно гладкими, то для вычисления интеграла не следует применять высокоточные квадратуры, а лучше ограничиться такими формулами, как формулы трапеций и прямоугольников.
3.2. Квадратурный метод решения интегральных уравнений Вольтерры.
Так как параметр λ в линейных интегральных уравнениях Вольтерры, в отличие от уравнения Фредгольма, не несет такой нагрузки, положим его равным единице и будем численно решать уравнение

Учитывая что уравнение Вольтерры формально можно считать уравнением Фредгольма вида:

K(t, s)=
для нахождения решения рассматриваемого уравнения воспользуемся результатами предыдущей главы.
Введем в рассмотрение временную сетку 


Составим систему линейных алгебраических уравнений, аналогичную системе (1), которая в силу свойств ядра интегрального уравнения вырождается в треугольную:
Из данной системы видно, что искомые значения 

Глава IV. Прикладные задачи, использующие решение интегральных уравнений.
4.1. Расчет теплоизоляции.
По стальному горизонтальному трубопроводу (






Определить наружный диаметр изоляции 






Упрощающие предположения: течение воды в трубе является термически стабилизированным; между сталью и асбестом существует идеальный тепловой контакт; теплопроводности стали и асбеста не зависят от температуры[12].
Вывод расчетных соотношений
Расчетная модель — бесконечная цилиндрическая труба, режим стационарный, объемных источников тепла в трубе нет. Уравнение теплопроводности имеет вид:
В цилиндрической системе координат получаем:
Граничные условия (закон Ньютона — Рихмана):
(положительным считается тепловой поток, идущий от центра )
Произведем замену переменных: 







где 


(т. к. 

C другой стороны:
Приравнивая выражения для 
Тепловой поток, проходящий через стенку трубы на единице длины:
где
т. е. 

Окончательные расчетные формулы для определения температур (с учетом того, что 
Для определения коэффициентов теплопередачи используются эмпирические формулы для переходного режима течения (


Поскольку 




Аналогично для естественной конвекции:


Теплофизические свойства воды и воздуха берутся из книги [“Задачник по технической термодинамике и теории тепломассообмена” Под. ред. и Петражицкого , “Высшая школа” , 1986].
Задача решается методом последовательных приближений, первое приближение 
на каждом шаге производя уточнение 




4.2. Фильтр Калмана.
Представим себе некоторую систему, состояние которой в любой момент времени однозначно характеризуется определенным набором величин (например, координаты, скорости, уровни напряжения и т. д.), как правило, недоступных для непосредственного определения. Говоря терминами векторной алгебры, эти величины являются элементами вектора состояния системы, отнесенного к заданному моменту времени. Кроме того, имеется ряд переменных, некоторым образом связанных с состоянием системы, которые можно измерить с заданной точностью; такие величины составляют вектор измерений, относящихся к определенному моменту времени. Алгоритм фильтра Калмана позволяет в реальном времени построить оптимальную оценку состояния системы, основываясь на измерениях, неизбежно содержащих погрешности; при этом вектор измерений рассматривается в качестве многомерного выходного сигнала системы, отягощенного шумом, а вектор состояния — неизвестный многомерный сигнал, подлежащий определению. Условием оптимальности построенной оценки состояния является минимум ее средней квадратической ошибки[13].
Указанный критерий признан наиболее общим; доказано, что применение множество других подобных условий (например, среднее арифметическое некоторой непрерывно возрастающей, симметричной функции, такой как абсолютная величина) приводит к тому же решению (функция модуля не обладает непрерывной производной, что существенно затрудняет ее применение в алгоритмах минимизации). Фильтр Калмана явился существенным усовершенствованием своего предшественника — алгоритма, позволяющего с помощью метода наименьших квадратов выделять скалярный сигнал из шума с неизменными статистическим характеристиками, предложенного в 40-х годах XX столетия Н. Винером.
Начальными условиями на каждом новом цикле алгоритма служат оценка состояния системы и величина, характеризующая ее погрешность. В случае скалярной переменной такой характеристикой является дисперсия, которая тем больше, чем сильнее разброс индивидуальных значений относительно истинного. Распространенная оценка дисперсии — среднеквадратическое отклонение, то есть квадрат стандартного отклонения, — выражает степень разброса величины относительно среднего. Обобщением дисперсии для вектора, то есть совокупности скалярных величин, служит ковариационная матрица. Ее диагональные элементы являются дисперсиями соответствующих составляющих вектора, а недиагональные — ковариациями, характеризующими взаимосвязь между парой составляющих. Совокупность измерений, отнесенных к каждому из моментов времени, обобщает вектор измерений. Алгоритм последовательно обрабатывает вновь поступающие векторы измерений, учитывая при этом значения, вычисленные на предшествующем цикле. Эта особенность отличает алгоритм фильтра Калмана от нерекуррентных алгоритмов, которым для работы требуется хранить весь массив обрабатываемых данных[14].
На следующем шаге с помощью обрабатываемых на данном цикле измерений уточняются начальные условия. Для этого алгоритм вычисляет вес поправок к ним на основе ковариационных матриц оценки состояния и измерений. Чем меньшей погрешностью характеризуются измерения по сравнению с оценкой состояния системы, тем больший вес они получат. Относительные веса неизвестных, определяющих вектор состояния системы, зависят от степени их влияния на вектор измерений: больший вес получат те переменные, вклад которых в измерения больше.
Уточнение начальных условий на основе поступивших на данном цикле измерений, в общем случае, приводит к уменьшению неопределенности в оценке состояния системы. Исправленные таким образом начальные условия и являются выходными данными фильтра Калмана на каждом цикле. На заключительном этапе работы алгоритма происходит подготовка к поступлению нового вектора измерений. На основе заданного линейного преобразования, связывающего последующий вектор состояния с предыдущим, прогнозируется оценка состояния системы, отнесенная к моменту следующего измерения. При построении ковариационной матрицы прогнозируемого вектора состояния фильтром Калмана учитывается возможность искажения модели, описывающей поведение системы, некоторым случайным процессом с известными статистическими параметрами. Поскольку конкретные значения возмущающего эффекта не могут быть известны, данное обстоятельство способствует повышению неопределенности прогноза[15].
По мере последовательной обработки новых измерений происходит накопление фильтром полезной информации, поэтому если элементы вектора состояния уверенно выражаются через измеренные величины, то суммарная погрешность оценок, как правило, должна снижаться. Однако поскольку вместе с улучшением точности оценок на этапе их уточнения имеет место ее снижение при построении прогноза, то эти тенденции, компенсируя друг друга, в последствии приведут к стабилизации неопределенности, характеризующей оценку состояния системы. В случае отсутствия фактора, вносящего возмущения в процесс перехода системы из одного состояния в другое, погрешность оценок в итоге достигнет нуля. Изменяющаяся в процессе работы алгоритма степень неопределенности оценки состояния системы влечет за собой и изменение весов, вычисляемых на втором шаге; данное обстоятельство выделяет фильтр Калмана как алгоритм с переменными весами.
Если состояние рассматриваемой системы неизменно, то алгоритм фильтра Калмана сводится к последовательной форме классического метода наименьших квадратов, в котором матрица, обратная ковариационной, выступает в качестве весовой. Другими словами, фильтр Калмана является, по существу, рекуррентным способом решения задачи уравнивания по методу наименьших квадратов. Данная задача впервые решена в 1795 году, результаты были опубликованы в работе 1809 года под названием “Теория движения небесных тел”, в которой он применил метод наименьших квадратов к определению элементов орбит небесных тел (см. раздел “Замечания Гаусса”). Все изложенные в этой работе положения, касающиеся эффективности применения данного метода при обработке результатов измерений в равной степени относятся и к фильтру Калмана.
Применение фильтра Калмана в спутниковой навигационной аппаратуре.
Когда применение инерциальной навигационной системы становится нецелесообразным, как, например, в одиночных GPS приёмниках, ее заменяют уравнениями движения объекта, навигационные данные которого подлежат определению, с задействованием петли обратной связи. Статистические параметры погрешностей, характеризующие модели состояния системы и измерений в фильтре Калмана, определяются тщательностью составления уравнений движения. Для статичного объекта они тривиальны и строги, однако в более сложных случаях неизбежны упрощения, которые приводят к накоплению погрешностей и значительному снижению точности по сравнению с опорной траекторией, определяемой инерциальным методом. Преимущество подобной схемы применения фильтра Калмана по сравнению с обычным решением задачи определения координат по методу наименьших квадратов кроется в сглаживании выбросов случайных ошибок спутникового метода, что уменьшает их влияние на результаты навигационных определений.
Разработка навигационной системы, содержащей в своем составе фильтр Калмана, независимо от типа применяемого оборудования (инерциальная или спутниковая аппаратура, прочие устройства) заставляет учитывать ряд особенностей. Часть фильтра, занимающаяся ковариационным анализом, не требует для своей работы ни конкретных значений оценок состояния системы, ни измерений; необходимы только величины, характеризующие их погрешности. Данное свойство используется разработчиком для априорной оценки точности результатов, получаемых посредством того или иного вида аппаратуры, и тем самым позволяет осуществить выбор подходящего оборудования. В некоторых случаях приходится предварительно реализовывать алгоритм на компьютере и проверять его работу с различными начальными условиями. Далее с помощью методов статистического анализа следует убедиться в том, что реализованная в фильтре модель измерений соответствует своему реальному прототипу. Наконец, когда построенный фильтр удовлетворит всем требованиям, необходимо провести серию заключительных испытаний для оценки адекватности выбранного способа линеаризации задачи и локализации возможных ошибок вычислительного характера. В большинстве случаев расширенный вариант алгоритма с замкнутым контуром обратной связи позволяет значительно снизить нежелательные последствия линеаризации. Ошибки в вычислениях обычно вызваны ограниченной длиной машинного слова и наиболее ярко проявляются в ковариационных матрицах, которые становятся либо несимметричными, либо имеют отрицательные диагональные элементы, вследствие чего нарушается правильная работа фильтра Калмана. Влияние этого источника погрешностей можно снизить, удерживая большее число значащих цифр при вычислениях или применив численный алгоритм, менее чувствительный к ошибкам округления.
Алгоритм фильтра Калмана из-за своей кажущейся простоты и легкости реализации до сих пор является основным средством обработки измерений в навигационных системах, использующих спутниковый метод определений. Для установления весов поступающих измерительных данных требуются статистические характеристики их ошибок, а также уравнения, предоставляющие связь переменных, определяющих текущее состояние системы, с измерениями и между собой. Таким образом, фильтр Калмэна является инструментом, позволяющим на основе математической модели системы построить оптимальные оценки системных переменных по выполненным измерениям. К достоинствам алгоритма следует отнести его рекуррентную природу, эффективно проявляющуюся при работе в реальном времени, а также возможность априорной оценки точности получаемых результатов средствами самого алгоритма.
Листинг№1 Численное интегрирование
1. Функция, возвращающая значение интеграла функции помощью метода Симпсона
2. Функция, возвращающая значение интеграла с помощью формулы трапеции.


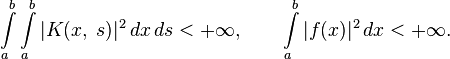
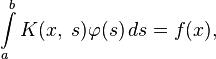
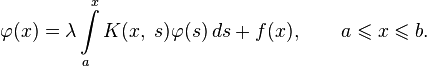
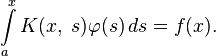

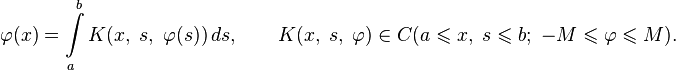

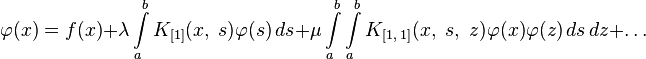

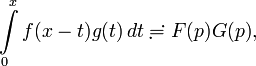
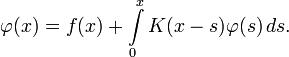

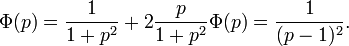
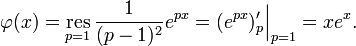


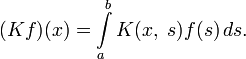
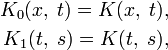





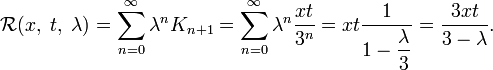


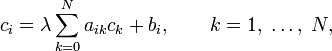

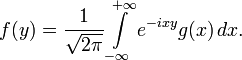

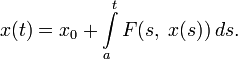

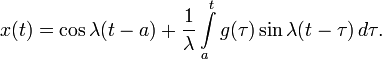
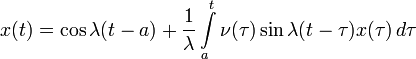
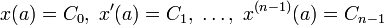

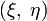 по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.
по некоторой кривой. Требуется определить эту кривую так, чтобы материальная точка, начав свое движение без начальной скорости в точке кривой с ординатой x , достигла оси Oξ за время t = f1(x) , где f1(x) — заданная функция.

































































































