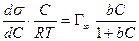Чем отличаются константы адсорбции в уравнениях ленгмюра и генри и какова взаимосвязь между ними

Видео:Уравнение ЛенгмюраСкачать

Лекция №3

План лекции:

1.Поверхностное натяжение — физический смысл.

Видео:Поверхностные явления: адгезия, смачивание, адсорбция | Коллоидная химияСкачать

АДСОРБЦИЯ

Поверхностная энергия стремится самопроизвольно уменьшиться. Это выражается в уменьшении межфазной поверхности или поверхностного натяжения ( s )

Вследствие этого стремления происходит адсорбция.

Адсорбция — процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемной фазой. Т.е. адсорбция может происходить в многокомпонентных системах, в слой переходит тот компонент, который сильнее уменьшает s .

Адсорбент — фаза определяющая форму поверхности, более плотная, может быть твердой или жидкой.

Адсорбат — вещество которое перераспределяется (газ или жидкость).

Десорбция — переход вещества из поверхностного слоя в объемную фазу.

Количественно адсорбцию описывают величиной Гиббсовской адсорбции (избыток вещества в поверхностном слое по сравнению с его количеством в объемной фазе, отнесенный к единице площади поверхности или единице массы адсорбента)

(3.1)

Г _i -Гиббсовская адсорбция,

V -объем системы,

с₀ -исходная концентрация адсорбата ,

с _{i —} концентрация адсорбата в объеме,

S — площадь поверхности раздела.

Все величины в (3.1) могут быть установлены экспериментально.

Адсорбцию можно рассматривать как процесс превращения поверхностной энергии в химическую.

Выведем соотношение между поверхностным натяжением и химическими параметрами компонентов.

Если объем поверхностного слоя равен 0, то

т.к. внутр. энергия пропорциональна экстенсивным величинам, то:

полный дифференциал от тех же переменных запишется следующим образом:

dU=T dS + S dT + s dS +S d s + å m _i dn _i + å n _i d m (3.3)

Подставляя dU из 3.2 в 3.3, получим:

3.4 и 3.5 — уравнения Гиббса для межфазной поверхности (поверхностного слоя).

Все экстенсивные величины поверхности зависят от площади поверхности , поэтому удобнее относить эти параметры к единице площади поверхности. Разделив уравнение 3.5 на площадь поверхности, получим:

=> (3.6)

Г _i — поверхностный избыток компонента i в поверхностном слое (по сравнению с его равновесной концентрацией в объемной фазе), то есть величина Гиббсовской адсорбции.

Уравнение 3.6 — фундаментальное адсорбционное уравнение Гиббса. Это строгое термодинамическое соотношение, написанное для многокомпонентной системы. Однако, практиче ское его использование неудобно. Оно, например, не раскрывает зависимость поверхностного натяжения от адсорбции конкретного вещества при постоянных химических потенциалах других веществ.. Единицы величины гиббсовской адсорбции определяются единицами химического потенциала. Если потенциал отнесен к молю вещества, то величина адсорбции выражается в молях на единицу площади.

Адсорбция конкретного вещества при постоянных химических параметрах других веществ:

Принимая во внимание , что m _i = m _i o + RT ln a_i, m _i и m _i o — равновесное и стандартное значения химического потенциала адсорбата i , а _i — термодинамическая активность адсорбата, d m _i = RT d ln a_i ,получим :

для Гиббсовской адсорбции:

(3.7)

3.7. применяют только тогда, когда можно использовать концентрации вместо активностей и пренебречь изменениями концентраций других веществ при изменении концентрации одного вещества. Этим условиям удовлетворяет разбавленный раствор относительно данного компонента. В таком растворе при изменении концентрации растворенного вещества практически не изменяется концентрация растворителя. Поэтому для растворенного вещества уравнение 3.7 переходит в широко используемые адсорбционные уравнения Гиббса для неэлектролитов и электролитов

(3.8)

(3.9)

Видео:АдсорбцияСкачать

УРАВНЕНИЕ ГЕНРИ, ФРЕЙНДЛИХА, ЛЕНГМЮРА

Для описания процесса адсорбции, помимо фундаментального уравнения адсорбции Гиббса, применяют ряд других аналитических уравнений, которые называются по имени их авторов.

При незначительном заполнении адсорбента адсорбатом отношение концентрации вещества в адсорбционном слое и в объеме стремится к постоянному значению, равному к_Г:

Это уравнение характеризует изотерму адсорбции при малых концентрациях адсорбата (рис.3.1, участок 1) и является аналитическим выражением закона Генри. Коэффициент к_Г не зависит от концентрации и представляет собой константу распределения, характеризующую распределение вещества в адсорбционном слое по отношению к его содержанию в объемной фазе. Уравнение Генри соблюдается приближенно, но это приближение достаточно для практики.

В более общем виде зависимость адсорбции от концентрации адсорбата можно определить с помощью уравнения Фрейндлиха.

Видео:Типы Химических Связей — Как определять Вид Химической Связи? Химия 9 классСкачать

Определение заряда коллоидной частицы (правило 6)

Правила составления мицелл

1. Основа мицеллы – агрегат, нерастворимый в данной дисперсионной среде, состоящий из множества (m) молекул (атомов) простого вещества.

2. Согласно правилу Пескова-Фаянса-Панета, на поверхности агрегата адсорбируются ионы электролита-стабилизатора, входящие в состав агрегата, либо имеющие общую природу с ним, либо специфически взаимодействующие с ним и находящиеся в избытке. Ионы, сообщающие агрегату поверхностный заряд, называются потенциалопределяющими. Агрегат + потенциалопределяющие ионы = ядро мицеллы.

3. Заряд ядра компенсируется эквивалентным количеством противоположно заряженных ионов электролита-стабилизатора – противоионов. Часть противоионов, прочно связанных с ядром, входит в адсорбционныйслой. Агрегат + адсорбционный слой = коллоидная частица (имеет заряд).

4. Остальная часть противоионов образует диффузионный слой.

5. Суммы электрических зарядов коллоидной частицы и диффузионного слоя равны друг другу по абсолютной величине и противоположны по знаку.

6. Электрический заряд коллоидной частицы равен алгебраической сумме электрических зарядов потенциалопределяющих ионов и противоионов адсорбционного слоя.

7. Мицелла гидрофобного золя является электронейтральной, т.е. алгебраическая сумма электрических зарядов ионов всех слоев равна нулю

Для любого типа реакции одно из исходных веществ берут в избытке по сравнению со стехиометрически необходимым соотношением:

Na3AsO3+ 3AgNO3→ ↓Ag3AsO3+ 3NaNO3

Электролитическая диссоциация электролита, взятого в избытке:

Na3AsO3« 3Na++ AsO33-

Агрегат Потенциалоп- Противоионы Ионы

ределяющие адсорбционного диффузионного

ионы слоя слоя

Адсорбционный слой Диффузионный слой

Здесь m, n, x – натуральные числа;

m – число молекул в агрегате;

n – число потенциалопределяющих ионов;

(n – x) – число противоионов адсорбционного слоя;

x – число противоионов диффузного слоя.

Численный коэффициент 3 перед (n – x) и х поставлен ввиду трехосновности аниона AsO33-.

Определение заряда коллоидной частицы (правило 6)

Для проверки правильности записи формулы мицеллы подсчитывают алгебраическую сумму зарядов всех ионов (правило 7):

Коллоидная частица имеет отрицательный заряд, мицелла в целом электронейтральна.

МИЦЕЛЛООБРАЗОВАНИЕ В РАСТВОРАХ

1. Какие вещества называют поверхностно-активными (ПАВ)?

2. Как классифицируют ПАВ?

3. Чем отличаются коллоидные ПАВ от истинно растворимых? Что называется критической концентрацией мицеллообразования (ККМ)?

4. Что такое поверхностная активность коллоидных ПАВ?

5. Как зависит форма мицелл от концентрации ПАВ в растворе? Каким образом ориентируются молекулы ПАВ в мицеллах в полярной и неполярной средах?

6. Какое явление называют солюбилизацией? Чем обусловлено это явление? Каково практическое значение этого явления?

7. Факторы, влияющие на ККМ в растворах ПАВ:

1) влияние длины углеводородного радикала на ККМ в разных по полярности растворителях;

2) влияние природы полярной группы молекулы ПАВ;

3) влияние добавокиндифферентного электролита на ККМ ионогенных и неионогенных ПАВ;

4) зависимость мицеллообразования от температуры, точка Крафта.

8. Условия образования мицеллярных растворов ПАВ.

9. Методы определения ККМ. Почему при концентрации выше ККМ поверхностное натяжение растворов ПАВ не изменяется?

10. Как влияет явление мицеллообразования на подвижность ионов?

1. Что такое защитное действие ВМС?

2. Механизм образования защитного действия.

3. Что такое флокуляция?

4. Что такое сенсибилизация?

5. Действие стабилизаторов.

6. Особенности белков как стабилизаторов. Смешанные пленки.

7. Влияние заряда на прочность макромолекул.

8. Что такоеосмотическое расклинивающее давление?

1. Перечислить три механизма образования двойного электрического слоя (ДЭС).

2. Строение ДЭС.

3. Факторы, влияющие на z-потенциал:

б) добавка индифферентного электролита;

в) добавка неиндифферентного электролита;

д) концентрация золя;

ж) природа дисперсионной среды.

4. Особенности белковых веществ как коллоидов: строение ДЭС в кислой и щелочной средах.

5. Обоснование возможности разделения белков электрофорезом.

6. Изоэлектрическая точка белков.

АДСОРБЦИЯ И ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ НА ГРАНИЦЕ «ЖИДКОСТЬ-ГАЗ»

1. Что называется поверхностным натяжением? Единицы измерения?

2. Методы измерения поверхностного натяжения (4 самых распростра-ненных метода).

3. Что лежит в основе определения поверхностного натяжения по методу Ребиндера? Работа установки. Формула расчета поверхностного натяжения по методу наибольшего давления воздуха в пузырьке.

4. Зависимость поверхностного натяжения жидкости от температуры.

5. Почему жидкость стремится принять форму шара?

6. *Что такое поверхностно-активные вещества? Их структура? Привести примеры.

7. Как поверхностное натяжение зависит от концентрации для ПАВ (поверхностно-активных веществ) и ПИВ (поверхностно-инактивных веществ)?

8. Понятие Гиббсовской адсорбции, её размерность и физический смысл.

9. Зависимость Гиббсовской адсорбции от концентрации, от температуры.

10. Что такое поверхностная активность вещества? Анализ уравнения Гиббса.

11. Как определить поверхностную активность графическим методом?

12. У какого из этих веществ поверхностная активность будет больше: СН3СООН; С2Н5СООН; С3Н7СООН и т.д.?

13. Понятие предельной адсорбции.

14. Как определить площадь, приходящуюся на одну молекулу в насыщенном адсорбционном слое? Зависит ли эта площадь от длины радикала?

15. Как определить линейные размеры молекулы ПАВ по величине адсорбции?

16. Какие характеристики и величины можно рассчитать, исходя из уравнения Гиббса?

АДГЕЗИЯ, СМАЧИВАНИЕ И РАСТЕКАНИЕ ЖИДКОСТЕЙ

1. Что такое адгезия? Определение, единицы измерения. Работа адгезии.

2. Что такое когезия? Определение, единицы измерения. Работа когезии.

3. Уравнение Дюпре. Условие растворения.

4. Что такое смачивание? Нарисовать векторы сил, действующих на каплю жидкости, помещенную на твердую поверхность.

5. Что такое краевой угол смачивания? Как по нему оценить гидрофильность/гидрофобность поверхности?

6. Закон Юнга.

7. Уравнение Дюпре-Юнга.

8. Растекание жидкости. Эффект Марангони.

МОЛЕКУЛЯРНАЯ АДСОРБЦИЯ НА ГРАНИЦЕ РАЗДЕЛА

«ЖИДКИЙ РАСТВОР – ТВЕРДЫЙ АДСОРБЕНТ»

1. Что называется адсорбцией? Что такое адсорбент, адсорбат и адсорбтив? Количественные характеристики адсорбции (абсолютная и избыточная величины).

2. Дайте определение изотермы, изостеры и изопикны адсорбции. Их графическое построение.

3. При каких условиях соблюдается при адсорбции закон Генри? Физический смысл константы Генри?

4. Уравнение изотермы мономолекулярной адсорбции Ленгмюра. Анализ его, физический смысл входящих в него величин. При каких условиях это уравнение применимо?

5. Чем отличаются константы адсорбции в уравнениях Ленгмюра и Генри, какова взаимосвязь между ними?

6. Уравнение Фрейндлиха, физический смысл входящих в него констант. Область применения.

7. Как определяют константыуравнения Ленгмюра и Фрейндлиха?

8. Какие геометрические характеристики можно рассчитать, зная константы уравнения Ленгмюра?

9. Какова ориентация молекул ПАВ на поверхности адсорбента в случае предельной адсорбции (нарисовать)? Чем определяется величина площади молекулы в адсорбционном слое?

10. Какие формулы используют для расчета величины адсорбции из экспериментальных данных?

11. На чем основано измерение удельной поверхности твердых адсорбентов?

12. Чем отличается адсорбция из растворов от адсорбции газовипаров?

ОПТИЧЕСКИЕ МЕТОДЫ АНАЛИЗА ДИСПЕРСНЫХ СИСТЕМ

1. Какие оптические явления наблюдаются при падении луча света на дисперсную систему? Какие методы исследования дисперсных систем основаны на этих явлениях?

2. Какие оптические методы используются для определения размеров частиц дисперсных систем? Укажите границы применимости (по дисперсности) этих методов.

3. Чем обусловлено светорассеяние в дисперсных системах и истинных растворах? Какими параметрами количественно характеризуют рассеяние света в системе?

4. Какова связь между оптической плотностью и мутностью «белых» золей? Для каких дисперсных систем применимо уравнение Рэлея?

5. Как влияют размеры частиц на зависимость оптической плотности «белых» золей от длины волны падающего света?

6. Чем различаются методы нефелометрии и турбидиметрии? Какие уравнения используются для определения характеристик рассеяния света?

7. Для каких дисперсных систем применимо уравнение Дебая? Какие параметры дисперсных систем определяют по методу Дебая?

8. В чем заключаются особенности метода ультрамикроскопии? Для каких дисперсных систем применим этот метод? Какие характеристики дисперсных систем могут быть определены этим методом?

Лабораторная работа № 10

СЕДИМЕНТАЦИОННЫЙ АНАЛИЗ СУСПЕНЗИЙ

1. Понятие о дисперсных системах, количественные характеристики дисперсных систем (Лекция №1).

2. Цель седиментационного анализа. Практическое применение результатов седиментационного анализа.

3. Методика седиментационного анализа.

4. Закон Стокса. Номограмма Стокса, её использование.

5. Что такое седиментация? Какие силы действуют на частицу?

6. Напишите уравнение Стокса для скорости оседания частиц. Каков физический смысл входящих в него величин? Изменением каких параметров системы можно изменять скорость осаждения частиц?

7. Кривая седиментации полидисперсной системы. Как определяют размеры частиц, используя кривую седиментации?

8. Определите по графику массу фракции, радиус частиц которой равен или больше радиуса в данной точке.

9. Определите по графику массу фракции для заданного интервала размеров (например от радиуса r3до r4).

10. Что можно определить, используя дифференциальную кривую распределения частиц по размерам?

11. Как определить содержание частиц для данного интервала размеров по дифференциальной кривой распределения?

12. Как рассчитать удельную поверхность дисперсной фазы Sуд?

Видео:Практическое занятие 6. Адсорбция на границе раствор – газСкачать

Лекция 13. Адсорбция

13.1. Уравнение адсорбции Гиббса

Строгое определение понятия адсорбции по Дж. Гиббсу: адсорбцией данного компонента на границе раздела двух фаз называется разность между фактическим количеством этого компонента в системе и тем его количеством, которое было бы в системе, если бы концентрации в обеих сосуществующих фазах были постоянны вплоть до некоторой геометрической поверхности, разделяющей их.

Эта разность может быть положительной или отрицательной. Она обозначается символом G (гамма) и имеет размерность моль/м 2 . Эту величину называют избыточной адсорбцией по Дж. Гиббсу.

Хотя в приведенном определении адсорбция отнесена к геометрической поверхности, не имеющей толщины (что удобно при выводе уравнений), фактически граница между фазами представляет собой очень тонкий слой (поверхностный слой), в котором все свойства отличаются от свойств объемных фаз и изменяются не скачкообразно, а непрерывно.

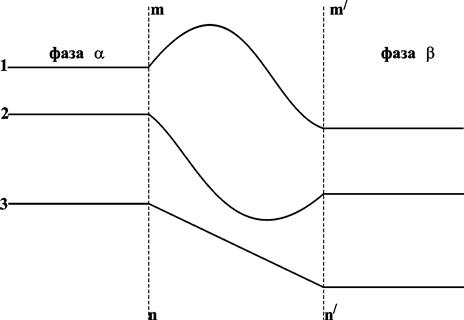
На рис. 13.1 показано возможное изменение концентрации вблизи границы раздела: концентрация компонента может быть как выше концентраций в обеих фазах (1), так и ниже (2) или иметь промежуточное значение. Эта область может рассматриваться как поверхностный слой. Таким образом, изучая границу раздела фаз, нужно рассматривать состояние трех фаз: двух объемных и одной поверхностной.

Рис. 13.1. Изменение концентрации компонентов у границы раздела фаз;
поверхностный слой – mn-m’n’

Уравнение, устанавливающее связь между всеми параметрами процесса адсорбции – величиной поверхностного натяжения s, концентрацией компонента [C] в одной из фаз, его адсорбцией Г, было выведено Дж. Гиббсом в 1876 г. Это уравнение является общим термодинамическим уравнением, справедливым для любых составов и природы поверхности раздела фаз.

Рассмотрим систему, состоящую из двух компонентов 1 и 2 и двух фаз a и b, разделенных поверхностью раздела с площадью S. Общее число молей каждого компонента в системе равно n₁ o и n₂ o . Если считать, что поверхностный слой не имеет толщины, т.е. представляет собой геометрическую поверхность, то обе объемные фазы будут иметь постоянный состав вплоть до этой геометрической поверхности. Обозначим число молей каждого компонента в каждой из этих фаз соответственно через n₁ a ,n₁ b ; n₂ a ,n₂ b . Так как на поверхности имеет место адсорбция, то, очевидно, n₁ o ¹ n₁ a + n₁ b и n₂ o ¹ n₂ a + n₂ b .

По вышеприведенному определению адсорбция каждого компонента Г₁ и Г₂ , отнесенная к единице площади поверхности, равна

. (13.1)

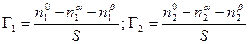
Чтобы найти Г₁ и Г₂, напишем уравнение энергии Гиббса для двух фаз a и b в отдельности и для всей системы в целом. В последнем случае, очевидно, нужно включить в уравнение член sdS:

dG o = — S o dT + V o dP + sdS + m₁dn₁ o + m₂dn₂ o . (13.2)

Укажем на уравнение Гиббса-Дюгема, которое устанавливает связь между химическими потенциалами:

dG = — S dT + VdP + Sm_idn₁ (P, T – постоянные). (13.3)

Тогда для бинарной системы получим

Интегрируя это уравнение при постоянных значениях m₁ и m₂, получим

Из (13.4) и (13.6) вытекает, что

. (13.7)

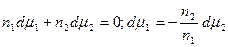
Это уравнение носит название уравнения Гиббса-Дюгема и связывает изменение химических потенциалов компонентов. Тогда с учетом уравнения Гиббса-Дюгема и поверхностных явлений получаем:

Сложение двух первых уравнений и вычитание полученной суммы из третьего дает

. (13.9)

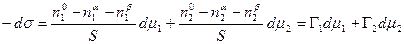
В качестве примера рассмотрим две конкретные системы: двухкомпонентный жидкий раствор, находящийся в равновесии со своим двухкомпонентным насыщенным паром, и твердое тело, находящееся в равновесии с однокомпонентным газом, совершенно не растворимым в этом твердом теле.

Поскольку в первом случае точное положение разделяющей геометрической поверхности несколько условно, то можно выбрать положение ее, при котором

Во втором случае вследствие нерастворимости газа в объеме твердого тела, объемные свойства этого тела, в частности его химический потенциал, не изменяются при адсорбции. Приписывая твердому телу индекс 1, имеем:

В обоих случаях получено одно и то же уравнение. Поэтому можно считать, что адсорбционное уравнение Гиббса имеет вид:

Оно является основным в учении о поверхностных явлениях.

Рассмотрим далее реальный раствор. Для реального раствора

где а – активность, тогда:

Подставив это значение в уравнение (13.12), получим:

ds = — Г Rt d lna,

. (13.13)

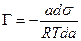
В разбавленных растворах а » С (где С – концентрация)

, (13.14)

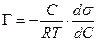
а для идеального или разреженного идеального газа

. (13.15)

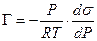
Уравнение (13.14) показывает, что если при адсорбции поверхностное натяжение s уменьшается с ростом концентрации С, т.е. ds/dC 0 и Г – отрицательно. Это соответствует поверхностно-инактивным веществам. Если известна зависимость s от С (т.е. изотерма поверхностного натяжения s = f(C) , то по уравнению Гиббса можно для каждого значения концентрации найти ds/dC и по уравнению Гиббса вычислить значение Г, т.е. построить изотерму адсорбции.

13.2. Обзор сорбционных явлений

Адсорбция на границе раздела твердое тело/газ. В общем случае явления, связанные с перераспределением веществ между различными частями гетерогенной системы, называются сорбцией. Сорбция (от лат. sorbeo – сгущать) – это изменение концентрации (часто увеличение) либо у поверхности раздела фаз (адсорбция), либо в объеме одной из фаз (абсорбция). Например, образование раствора за счет поглощения НСl (газа) и поглощение газа металлом (абсорбция). Поверхностная сорбция – адсорбция.

Твердое тело, у поверхности которого происходит адсорбция, называется адсорбентом, адсорбирующийся газ или адсорбирующийся компонент жидкого раствора – адсорбтивом, а адсорбированое вещество – адсорбат.

В строгом определении адсорбции она рассматривается как избыток вещества вблизи поверхности по сравнению с равным объемом вдали от нее. В ряде случаев удобнее рассматривать не избыток, а все количество адсорбата вблизи поверхности. Это количество обозначают символом а и называют полным содержанием, или просто адсорбцией (без указания гиббсова). Так как для пористых твердых тел бывает затруднительно знать величину поверхности, то часто адсорбцию относят не к единице поверхности, а к единице массы (моль/кг или моль/г).

Адсорбция самопроизвольна и протекает при Р = const со снижением энергии Гиббса, а при V = const – со снижением энергии Гельмгольца. Однако при этом происходит не выравнивание концентраций по всему объему системы, а увеличение разности концентраций между газовой фазой (раствором) и поверхностью. Одновременно уменьшается подвижность сорбирующихся молекул. Оба фактора ведут к уменьшению энтропии (DS o , так как DG o = DH o + TDS o ,

. (13.26)

. (13.27)

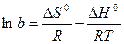
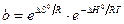
Таким образом, адсорбционный коэффициент b связан со стантартной энтропией DS° и со стандартной теплотой адсорбции q = –DH°.

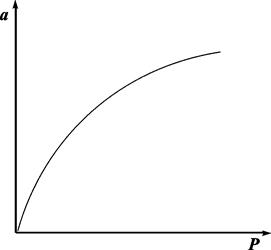
Очень часто а_m называют «емкость монослоя». На рис.13.3 показана кривая, выражающая изотерму адсорбции по Ленгмюру

Рис. 13.3. Изотерма адсорбции по Ленгмюру

При очень малых заполнениях и, следовательно, очень малых давлениях Р в знаменателе, согласно (13.25), bр > 1 и а = а_m, т.е. величина адсорбции перестает зависеть от давления, поскольку все центры уже заняты.

Для расчета параметров a_m и b уравнение Ленгмюра представляют в виде

. (13.28)

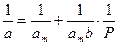
Тангенс угла наклона этой линии равен 1/a_mb, а отрезок, отсекаемый на оси ординат, равен 1/a_m.

Уравнение Ленгмюра, полученное на основании модели локализованной адсорбции газов на поверхности твердого тела, часто хорошо описывает адсорбцию растворенных веществ на поверхности жидкости (поверхность раздела раствор/газ), при которой адсорбция не локализована, так как молекулы подвижны и образуют двумерную газо- или жидкообразную пленку.

Обусловлено это тем, что основные положения модели Ленгмюра соблюдаются при адсорбции из растворов: поверхность жидкости идеально однородна, взаимодействие адсорбированных молекул в адсорбционном слое мало отличается от их взаимодействия в растворе. Оно к тому же ослаблено за счет взаимодействия молекул растворенного вещества с молекулами растворителя и практически не влияет на адсорбцию.

Уравнение Ленгмюра связано с уравнением состояния адсорбционной пленки – уравнением Гиббса. Так,

,

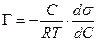
а по уравнению Ленгмюра

;

. (13.29)

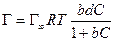
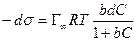
После интегрирования в пределах от s_о до s и от 0 до С получим:

,

, (13.30)

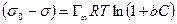
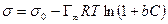
где Г_¥ связано с площадью, занимаемой 1 моль адсорбированного вещества в мономолекулярном слое, следующим соотношением: .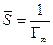

Дата добавления: 2016-02-09 ; просмотров: 2976 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

💡 Видео

Поверхностные явления. Адсорбция.Скачать

Скорость химических реакций. 9 класс.Скачать

Физическая химия #3. Первый, второй и третий порядки химической реакции. Времена полупревращенияСкачать

Теории кислот, оснований и растворов. Теория Аррениуса-Оствальда. 11 класс.Скачать

Названия в ОРГАНИКЕ | КАК ПРАВИЛЬНО называть химические вещества и элементы?Скачать

Как составлять УРАВНЕНИЯ РЕАКЦИЙ | БИНАРНЫЕ СОЕДИНЕНИЯ | ХИМИЧЕСКИЕ УРАВНЕНИЯСкачать

Коробов М. В. - Физическая химия II - Поправка Хиншельвуда. Мономолекулярные реакции в ТАКСкачать

25. Схема реакции и химическое уравнениеСкачать

АдсорбцияСкачать

Ионная, ковалентная и металлическая связиСкачать

Все ОВР с дихроматом для ЕГЭ 2023 | Интенсив | Екатерина Строганова | 100балльныйСкачать

Использование уравнения Аррениуса для решения задач (1/2). Химия для поступающих.Скачать

АдсорбцияСкачать

Нормализация. Термообработка | Матвед 11Скачать

Таблица Менделеева. Металлические и неметаллические свойства. Радиус атома.Скачать