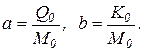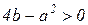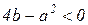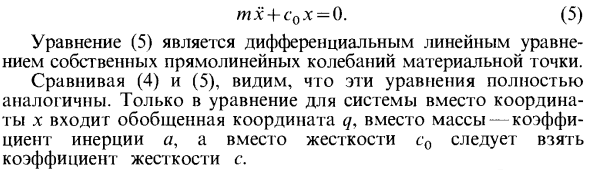
Частота собственных колебаний системы дифференциальных уравнений (2 видео)

Содержание

Дифференциальное уравнение собственных линейных колебаний системы
Дифференциальное уравнение собственных линейных колебаний системы
Колебания стержневых систем
Уравнение частоты собственных колебаний механической системы.
📽️ Видео

Видео:Видеоурок "Системы дифференциальных уравнений"Скачать

Дифференциальное уравнение собственных линейных колебаний системы

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Дифференциальное уравнение собственных линейных колебаний системы

Чтобы вывести линейное уравнение малых собственных колебаний из уравнения Лагранжа (1), кинетическая и потенциальная энергии должны быть последовательно расширены вблизи положения равновесия системы. Предположим, что система голономных, идеальных, неосвобожденных и фиксированных связей состоит из N точек и движется вблизи положения равновесия. Ее кинетическая энергия При сделанных предположениях о совместной стационарности радиус-вектор r * каждой точки в системе зависит от времени только через обобщенную координату q.

Следовательно, rk = — ^ q. Подставляя этот гк в выражение кинетической энергии, Как и в случае с gk, величина A может зависеть только от q, а не от q. Когда A (q) расширяется вблизи q = 0 степенного ряда, Далее индекс 0 означает, что соответствующее значение вычисляется с q = 0. Чтобы получить кинетическую энергию в терминах квадратичного и более низкого членов для q и q, достаточно получить только постоянное значение Ao из разложения A ( Людмила Фирмаль

Следовательно, выражение кинетической энергии путем отклонения третьего и более высоких членов можно выразить следующим образом. (2) Положительная постоянная а называется коэффициентом инерции. Обычно коэффициент инерции равен массе или моменту инерции. Потенциальная энергия системы P для стационарного силового поля и стационарной связи является функцией только обобщенной координаты q. Расширяясь до степенного ряда вблизи q = 0, получим Потенциальная энергия Po в равновесии при q = 0 принимается равной нулю.

Значение [dP / dts) 0 является значением обобщенной силы Q в положении равновесия системы и равно нулю. Предположим, что в равновесии потенциальная энергия минимальна. Это является достаточным условием устойчивости положения равновесия системы. В этом случае Значение OFm (d2P / dd2) 0 положительное, t «* ‘T x указывает, что константа (- • ——- «Они определяются коэффициентом жесткости Или просто жесткий. Рисунок, но, следовательно, уничтожить слабых Есть заказ более третичный n (q) = 1 / 2cq2- (3).

Система, в которой кинетическая энергия и потенциальная энергия точно представлены в соответствии с уравнениями (2) и (3) без отбрасывания членов более высокого порядка, называется линейной. Для них вся математическая система такая же, как и система, которая совершает небольшие колебания, но колебания линейной системы являются произвольными и необязательно малыми. Далее рассматриваются линейные колебания, включая небольшие колебания. На основании (2) и (3) вы получите.

Подстановка этих производных значений в уравнение Лагранжа (1) дает следующее дифференциальное уравнение для небольшой собственной вибрации системы с одной степенью свободы. aq + cq = 0. (4) Если третий и более высокий члены учитываются при расширении кинетической энергии и потенциальной энергии, второй и более высокий члены появляются в уравнении (4), и дифференциальное уравнение становится нелинейным. Получите дифференциальное уравнение для линейной вибрации точки массы, которая не обязательно мала. Масса M массой m движется линейно вдоль оси Ox под действием силы F.

Будем считать, что после присоединения точки становятся точками рассматриваемого тела, после отделения точки перестают взаимодействовать с телом и исключаются из дальнейшего рассмотрения. Людмила Фирмаль

Сила F линейно зависит от расстояния точки от положения равновесия O и стремится вернуть точку в положение равновесия (рис. 110). Поместите начало расстояния x в положение равновесия (точка O). Сила F направлена на начало расстояния (точка O). На данный момент он равен нулю. Проекция на ось О Fx = -cox, Где постоянная с0 — жесткость. Сила F в этом случае называется линейной восстанавливающей силой. Упругая сила согласно закону Крюка — это линейная восстанавливающая сила.

Подстановка значений линейной восстанавливающей силы в дифференциальное уравнение для линейного движения точек и преобразование всех членов в часть уравнения дает: mx + cox = 0. (5) Уравнение (5) представляет собой линейное дифференциальное уравнение естественной линейной вибрации точки массы. Сравнивая (4) и (5), вы можете видеть, что эти уравнения полностью аналогичны. Только в системных уравнениях вместо координаты x обобщенной координате q необходимо ввести коэффициент инерции a вместо массы и получить коэффициент c жесткости вместо жесткости c0.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

Видео:Собственные частоты колебаний точкиСкачать

Колебания стержневых систем

Колебания стержневых систем

Собственные колебания стержневых систем с присоединенными массами

Если конструкция выведена из состояния равновесия, то она будет колебаться относительно равновесного состояния (положения статического равновесия). Частоты колебаний определяется физическими свойствами конструкции. Если к конструкции не приложены внешние динамические силы или силы сопротивления, то выведенная из равновесия конструкция будет колебаться бесконечно долго. Такие колебания называются собственными колебаниями конструкции. Амплитуды, частоты и формы собственных колебаний зависят от физических свойств конструкции и начального неравновесного состояния.

Рассмотрим пружину жесткостью r (рис.1,а) Жесткость пружины — сила, вызывающая удлинение пружины на единицу длины [r] — H/см, H/м. Если к пружине подвешен груз массой m, то в условиях статического равновесия пружина удлинится, и груз переместится на расстояние (рис. 1,б). Начало координат далее будем связывать с положением груза в условиях статического равновесия. Если груз находится и движется по горизонтальной плоскости, то х0=0.

Если масса выведена из равновесного состояния (рис. 1,в), то на него действуют силы упругости пружин — , вес пружины mg и сила инерции .

Учитывая равенство нулю сил статического равновесия, получаем дифференциальное уравнение движение массы m, подвешенной на пружине

, или . (1)

где — частота собственных колебаний (число колебаний в единицу времени)

Из характеристического уравнения получаем — мнимые корни и, следовательно,

(2)

Положив , , получим уравнение (2) в виде

, (3)

где А — амплитуда колебаний; параметр a определяет начальное положение и начальную скорость движения массы :

; (рис. 2).

Если заданы начальное положение и начальная скорость движения массы, то получим

, . (4)

Рассмотрим стержень длиной l с подвешенной на конце грузом с массой m (рис. 3) (считаем, что вес самого стержня мал по сравнению с грузом и влиянием собственного веса будем пренебрегать). По действием силы F удлинение стержня . При удлинении стержня на единицу длины необходимо приложить силу . Следовательно стержень можно рассматривать как пружину с жесткостью . Если стержень с подвешенной на конце массой вывести из равновесия, то частота колебаний массы будет определятся формулой . Как и в случае пружины форма колебаний определяется формулой (3), от положения массы при статическом равновесии, определяемой удлинении весом массы .

Рассмотрим однопролетную, шарнирно опертую балку с грузом в пролете балки (рис. 4). Прогиб в балке в точке приложения можно определить на основе интеграла Мор по формуле

, где — прогиб в точке приложения единичной . При колебании балки с массой m в i-й точке () получаем дифференциальное уравнение колебаний присоединенной массы

. (5)

Очевидно, дифференциальное уравнение колебаний массы, расположенной в пролете балки, соответствует уравнению колебаний массы с пружиной жесткостью . Следовательно, груз на балке колеблется в соответствие с формулой (3) с частотой

Эти выводы справедливы для любой балки, в том числе консольной, шарнирно опертой балки с консолями и для статически неопределимой балки, при расположении на балке 1-й массы.

Рассмотрим балку с несколькими присоединенными массами (рис. 5).

При действии на балку сосредоточенных поперечных сил прогиб в i-ой точке (с координатой хi) определяется по формуле

,. (6)

— прогиб в i-ой точке от действия единичной поперечной силы в j-ой точке.

Записывая уравнение (5) в точках присо6едененных масс от действия сосредоточенных сил в точках присоединенных масс, получим:

;

; (7)

Здесь точки показывают, что число масс может быть больше (меньше) трех. Число уравнений и число слагаемых в каждом уравнении соответствует числу присоединенных масс.

При колебаниях балки в точках присоединенных масс действуют инерционные силы

(8)

Тогда, система уравнений (6) приводится к системе дифференциальных уравнений колебаний балки с присоединенными массами:

;

; (9)

Здесь, как и в предыдущих примерах, перемещения уi отсчитываются от положения каждой массы при статическом равновесия балки.

Упругая система балки приводит к условию колебаний присоединенных масс с одинаковой частой (или комбинации частот), в соответствии с формулой (3)

. (10)

Подставляя решение (10) в систему дифференциальных уравнений (9) и сокращая на общий множитель , получаем систему однородных алгебраических уравнений:

;

; (11)

Однородная система имеет нулевое решение Аi = 0. Однако это означает отсутствие колебаний, что нас не удовлетворяет. Из теории алгебраических уравнений известно: чтобы однородная система алгебраических уравнений имела не нулевое решение, определитель системы уравнений должен бать равен нулю:

. (12)

Разделив определитель на w2, получаем эквивалентный определитель в виде

, . (13)

Значение определителя зависит от значений присоединенных масс, значений dij и параметра l. Однако неизвестным параметром является только параметр l, и его значение подбирается из условия равенства нулю определителя. Параметр l называется в математике собственным числом матрицы (матрицы определяемой коэффициентами определителя d без параметра l.[ ].

Раскрывая определитель можно получить полином относительно параметра l

, (14)

где k — количество присоединенных масс балки.

Отметим, что все собственные числа матрицы, определяющей собственные частоты колебаний, определяются действительными числами (если при расчете не были допущены ошибки). Это соответствует физической сущности задачи.

В математике известны аналитические методы определения корней полиномов не болей 4-й степени. Для полиномов более 4-ой степени точные методы вычисления корней существуют только для частных случаев. Для остальных полиномов корни вычисляются только приближенными численными методами. Поскольку задача нахождения собственных чисел матрицы является задачей, встречающейся во многих технических и физических процессах, то разработаны численные методы ее решения. Практически во всех алгоритмических языках имеются подпрограммы для вычисления собственных чисел матриц. Имеется такая подпрограмма и в комплексе «MathCad». Использование этой подпрограммы будет показано ниже.

После определения собственных чисел матрицы, вычисляются собственные частоты балки с присоединенными массами . Амплитуды колебаний и параметр a зависят от начального положения масс и начальных скоростей .

Рассмотрим раму с присоединенными массами (рис. 6).

Частота собственных колебаний системы дифференциальных уравнений

При действии на раму сосредоточенных сил, справедлива формула (6) определения перемещения в i-той точке по заданному направлению. В отличие от балки, где присоединенная масса имеет одну степень свободы (поперечные прогибы балки), присоединенная масса рамы в плоскости может иметь две степени свободы ( горизонтальное и вертикальное перемещение), если перемещение не ограничено опорой.

Поэтому, прежде всего необходимо определить число степеней свободы присоединенных масс, связанные с изгибными деформациями рамы. Для этого, в заданной раме ставим дополнительные условные опоры, ограничивающие перемещения присоединенных масс, связанных с изгибными деформациями рамы (влиянием продольных деформаций стержней рамы пренебрегаем) (рис. 6,а). Дополнительные опоры на рис. 6,а. показаны пунктиром (условные опоры).

Вертикальное перемещение присоединенной массы m1 ограничено опорой А. Поэтому устанавливается только условная горизонтальная опора — 1. Вторая присоединенная масса имеет две степени свободы и требует установки вертикальной — 2 и горизонтальной — 3 условных опор. Условная опора 3 ограничивает горизонтальное перемещение всех присоединенных масс на горизонтальном стержне, и для них требуется установка только вертикальных условных опор условных опор: 4-я (присоединенная масса m4), 5-я (m6), 6-я (присоединенные массы m5 и m7). Для присоединенной массы m3 дополнительной условной опоры не требуется, так как ее вертикальное перемещение ограничено опорой А, о горизонтальное условной опорой — 3.

Отметим, что условная опора, ограничивающая перемещение присоединенных масс вдоль стержня, может быть установлена в любой точке этого стержня. Нумерация условных опор произвольна и может не совпадать с номером присоединенной массы, перемещение которой она ограничивает.

Для заданной рамы с 7-ю присоединенными массами (рис.6) установлено 6 условных опор, ограничивающих перемещения присоединенных масс. Следовательно, присоединенные массы (рама с присоединенными массами) имеют 6 степеней свободы.

Если присоединенные массы выведены из состояния статического равновесия, то происходит колебания системы с присоединенными массами. При колебании присоединенных масс, колебания происходят в направлении условных опор (перемещение уi). Все присоединенные массы, расположенные на одном стержне будут иметь одинаковое смещения (амплитуды колебаний, скорости и ускорения) вдоль стержня. Для учета инерционных сил введем понятие приведенных масс — масс колеблющихся в направлении i—ой условной опоры.

Для рамы с присоединенными массами (рис 6) имеем:

; ; ; ; ; .

Вывод уравнений колебаний рамы с присоединенными массами аналогичен выводу соответствующих уравнений балки с присоединенными массами. Число уравнений и слагаемых в них соответствует числу степеней свободы присоединенных масс и колебания происходят по направлению условных опор от действия приведенных масс. В результате получаем определитель.

. (15)

— перемещение по направлению i-ой условной опоры от единичной силы по направлению j-ой условной опоры (). Интегрирование производится по всем стержням рамы.

Рассмотрим пример определения частот колебаний рамы с присоединенными массами (рис. 7, а).

Условные дополнительные опоры и значения приведенных масс показаны на рис. 7,б. Присоединенные массы имеют 4 степени свободы. Для присоединенных масс получаем ; ; ; .

На рис. 7,б пронумерованы узловые точки, рама имеет 5 участков, на которых эпюры моментов от единичных сил в местах условных опор будут линейными.

Строим эпюры моментов в заданной раме от единичных сил в направлении условных опор. (рис. 8)

Пунктиром на участках показано отсутствие эпюры (изгибающие моменты на участке равны нулю).

Перемножая эпюры , , , по правилу Верещагина, получаем коэффициенты .

При перемножении эпюр учитываем длины и жесткости () участков, приведенные на рис. 7.

На стержнях с участками различной жесткости перемножение эпюр на каждом участке производится независимо. Если участки на стержне одинаковой жесткости эпюры могут перемножаться на каждом участке или на нескольких участках совместно для линейной эпюры на этих участках.

;

В скобках под формулами показаны номера участков, на которых перемножаются эпюры по правилу Верещагина

Учитывая, что все массы и коэффициенты dij имеют общие множители (m, a3/EJz) определи, умножаем на получая (определитель с безразмерными параметрами)

, (16)

где , (k1=4, k2=6, k1=1, k1=3); (, , , , , , , , , );

После вычисления собственных чисел матрицы , частоты колебаний системы с приведенными массами определяется по формуле .

Примечание. Собственные числа и частоты колебаний систем с присоединенными массами можно проводить без перехода к определителю с безразмерными параметрами, если все параметры (m, a3/EJz) на участках заданы.

Для определения частот колебаний рассматриваемой рамы используем программный комплекс «MathCad». Для вычисления собственных чисел матрицы в системе «MathCad».формируется матрица d коэффициентом матрицы без параметра l. Затем используется оператор . результат выводится на печать и используется для вычисления частот колебаний .

Фрагмент программы собственных частот колебаний рамы с присоединенными массами в системе «MathCad» (Коэффициенты dij вычисляются предварительно вручную):

Расчет частот собственных колебаний рамы с присоединенными массами

Коэффициенты dij

Матрица для вычисления собственных частот колебаний

Вычисление собственных чисел матрицы и собственных частот колебаний

Л и т е р а т у р а

1. Рекач устойчивости и динамики стержневых систем/ Конспект лекций для строителей. — М.: УДН, 1974. 108 с.

2. nОсновы динамики упругих систем. — М.: Изд-во РУДН, 1989. — 80 с.

3. Куприянов указания к расчету стержневых систем на динамическую нагрузку. — М.: Изд-во УДН, 1989. = 32 с.

Видео:Урок 327. Гармонические колебанияСкачать

Уравнение частоты собственных колебаний механической системы.

Любая техническая система в процессе своей эксплуатации подвержена воздействию внешних силовых факторов, которое определяется как входной сигнал. Результатом взаимодействия входного сигнала с технической системой является выходной сигнал. Следовательно, задача исследования технической системы состоит в ответе на вопрос: как входной сигнал преобразуется в выходной сигнал? То есть, возникает необходимость оценки количественных характеристик системы и возможности преобразования входного сигнала.

Исследование состояния системы необходимо начать с представления ее некой расчетной схемой и составления на основе учета действующих на систему сил уравнения ее движения.

В общем случае уравнение движения системы представляет собой дифференциальное уравнение в частных производных второго порядка по времени и четвертого порядка по пространственным координатам относительно функции перемещения точек системы. Исторически одним из первых методов, нашедших широкое применение при решении краевых задач для уравнений с частными производными, является метод разделения переменных, или метод Фурье, заключающийся в построении набора частных решений, каждое из которых разыскивается в виде произведения функций меньшего числа переменных (как правило, одного переменного). В ряде случаев оказывается, что такое представление не вступает в противоречие с исходным дифференциальным уравнением (тогда говорят, что уравнение допускает разделение переменных) и приводит в зависимости от размерности задачи к нескольким дифференциальным уравнениям, содержащим один и тот же числовой параметр. В зависимости от характера области, в которой решается краевая задача, граничных и начальных условий представляется возможным определить дискретные значения (иногда сплошной спектр) этих параметров, что приводит к совокупности частных решений, суммируя которые находят достаточно общее представление решения. Неизвестные коэффициенты (дискретные значения или некоторые функции) определяются уже на заключительном этапе при удовлетворении краевых условий.

В самом общем случае решение дифференциального уравнения движения системы может быть представлено в виде

;

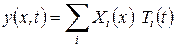(19)

где 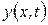— перемещение точек системы;

x — радиус-вектор точки системы;

Функция времени T(t) (индекс i опущен) определяется из обыкновенного дифференциального уравнения относительно времени t, и получаемого из общего уравнения движения после разделения переменных. В общем случае уравнение для определения T(t) имеет вид для случая постоянных коэффициентов:

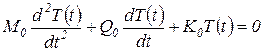(20)

для случая переменных коэффициентов:

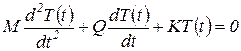(21)

В (20) и (21) М₀, М — соответственно постоянная и переменная матрицы масс; К₀, К — соответственно постоянная и переменная матрицы жесткости; Q₀, Q — соответственно постоянная и переменная матрицы, иногда называемые матрицей демпфирования, что верно лишь для частных случаев. В общем случае реальная механическая система представляет собой сложную комбинацию одномассовых и многомассовых систем и систем распределенными параметрами. Поэтому коэффициентами в уравнениях (20) и (21) в общем случае являются матрицы.

Из (20) следует, что характеристиками описываемого данным уравнением механического процесса являются спектр собственных чаете (собственных значений) 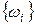и соответствующие им функции форм (собственные функции) Х_i(х). Характеристиками же описываемого уравнением (21) механического процесса являются спектр критических частот изменения параметра и область динамической неустойчивости. При этом спектр критических частот строится на основе спектра собственных частот уравнения с постоянными коэффициентами.

Спектр критических частот, область динамической неустойчивости и анализ уравнения с переменными коэффициентами является самостоятельной задачей, выходящей за рамки данного курса. Поэтому для первого знакомства с основами технической диагностики ограничимся только анализом собственных и вынужденных колебаний систем, уравнения движения которых описываются уравнениями с постоянными коэффициентами, а функция времени в решении (19) находится из уравнения (20).

Уравнение (20) может быть представлено в виде

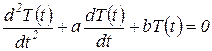(22)

где

Решение уравнения (22) зависит от соотношения между его коэффициентами. При

решение будет иметь вид

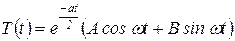(23)

где 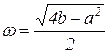— собственная частота.

решение имеет вид

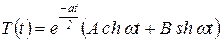(24)

где 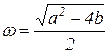— собственная частота.

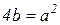
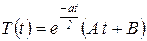При решение имеет вид

(25)

Функция времени (25) представляет собой суперпозицию двух монотонных процессов, численно выраженных экспонентой и линейной функцией времени. То есть, функция (25) не описывает процесса гармонических колебаний системы и поэтому не будет рассматриваться в рамках нашего курса.

Процессы, характеризуемые функцией времени (24), не являются характерными для рассматриваемой нами области техники. Поэтому в рамках нашего курса ограничимся рассмотрением процессов, характеризуемых функцией времени (23).

Согласно (23) функция времени зависит от угловой собственной частоты w, это означает, что частоты собственных колебаний системы, а следовательно, в более общем случае спектр собственных частот системы являются численными характеристиками, количественно отражающими состояние системы. В свою очередь, значение частоты зависит от массы, демпфирования и жесткости механической системы. Изменение любого параметра системы, количественно влияющего на эти матрицы, ведет к изменению частоты собственных колебаний, а следовательно, и к изменению функции времени.

Но влияние частоты не ограничивается только функцией времени. Покажем, что выражение каждой из функций формы в (19) зависит от соответствующего ей значения собственной частоты.

Дата добавления: 2018-09-24 ; просмотров: 1093 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ